无干涉双曲面加工范围研究

黄志东，谷 泉，张 雷

（1.辽宁科技学院机械工程学院，辽宁 本溪 117004；2.吉林大学机械科学与工程学院，吉林 长春 130025）

1 引言

随着数控技术与加工技术的飞速发展，各国学者对复杂曲面的制造越来越重视，对光学非球面透镜和叶片的应用也大幅度增加[1]。轴对称非球面具有关于轴线的旋转对称性，在工程应用中扮演十分重要的角色。例如，用一个或几个非球面元件代替多个球面元件，不仅可以达到矫正像差、简化装置结构，而且能够降低成本和减轻质量的目的[2]。文献[3-4]针对叶片加工提出了干涉检验规划算法。文献[5]提出一种轴对称非球面的数学描述。文献[6]将NURBS 建模方法应用到非球面。轴对称非球面的加工方法主要有平行磨削法[7-8]和圆弧包络磨削法[9]，文献[10]开发了一种双圆弧插补算法来加工非球面。文献[11]提出将六轴高精密机床用于加工非球面光学镜面。坐标测量法、干涉法和激光扫描法是非球面的主要测量方法[12]，此外，如何测量大型光学非球面[13]以及如何实现在线误差补偿[14]等问题也获得了一定的成果。

文献[15]推导了加工双曲面不发生干涉的参数准则，如图1 所示。切削角度α 与双曲面子午截面曲线的偏心率平方e2的函数关系满足第1 区域，加工过程中不会发生干涉现象；第2 区域表示干涉现象可能发生在工具与双曲面的右侧；第3 区域表示干涉现象可能发生在工具与双曲面的左右两侧；第4 区域则表示干涉现象可能发生在工具与双曲面的左侧。

然而，当α 与e2的函数关系位于第2、3、4 区域内，干涉现象与双曲面的口径大小是否存在一定的关系呢？如果存在，那么这个双曲面口径范围的极限值将变得意义重大。针对上述问题，建立加工双曲面的数学模型，分析加工双曲面的参数特征，推导刀具位于铅垂方向的位置、双曲面最大矢高、最大口径等关键技术指标的变化规律，获得了保证无干涉现象的双曲面加工范围。为加工双曲面的参数选取提供参考。

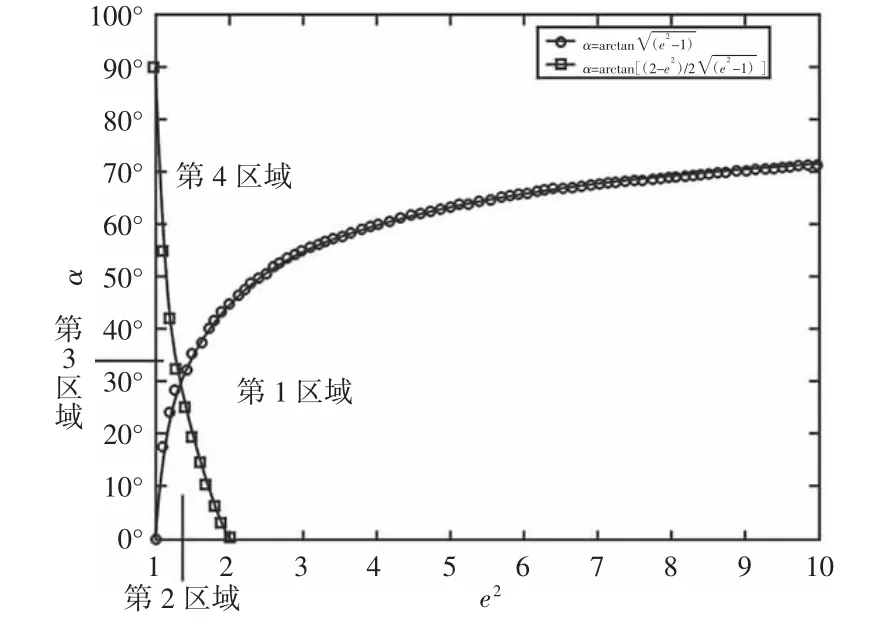
图1 α-e2 曲线Fig.1 The α-e2 Curve

2 加工双曲面的数学模型

加工双曲面的示意图，如图2 所示。

图2 双曲面加工示意图Fig.2 The Diagram for Machining Hyperboloidal Surface

刀具在加工双曲面的过程中，共有三种姿态：右倾、左倾和铅垂方向。

2.1 刀具右倾

轴对称非球面的子午截面曲线为二次曲线。建立直角坐标系，如图2（a）所示。将原点设在二次曲线的顶点O1，设Y 轴正方向与水平向右方向重合，设Z 轴正方向与竖直向上方向重合。过双曲线上的点O2（y2，z2），作双曲线的切线l0，斜率为k0。直线l2与刀具轴线重合，O3位于刀头中心，连接O2O3，作直线l1。α 为l1与l2的夹角。α 不同，对应的刀具切削点位置也不同。为了获得更好的表面质量，在双曲面的加工过程中，刀具切削点位置应尽量保持不变，即切削角α 不变。设刀具与工件的碰撞接触点为O4，刀具摆角为γ1。设刀具轴线为l2，过点O4向l2作垂线l4，垂足为O5。

根据坐标变换理论，O1坐标系可通过O1→O2（O′2）→O3→O5变换到O5坐标系。于是，可推导出变换矩阵［1T5］1为：

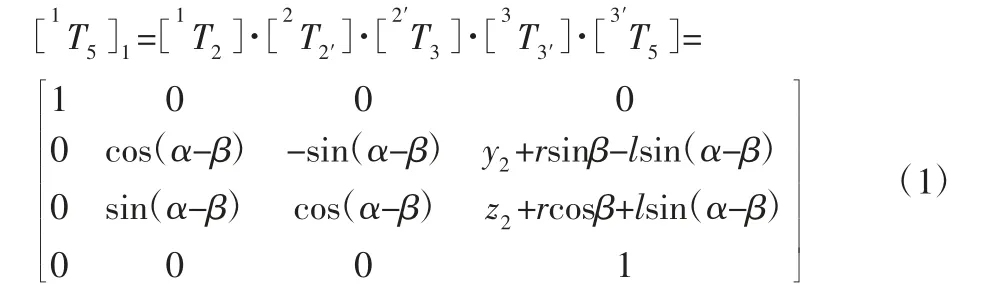
同时，O1坐标系也可通过O1→O4→O5变换到O5坐标系，从而得到变换矩阵为［1T5］2为：

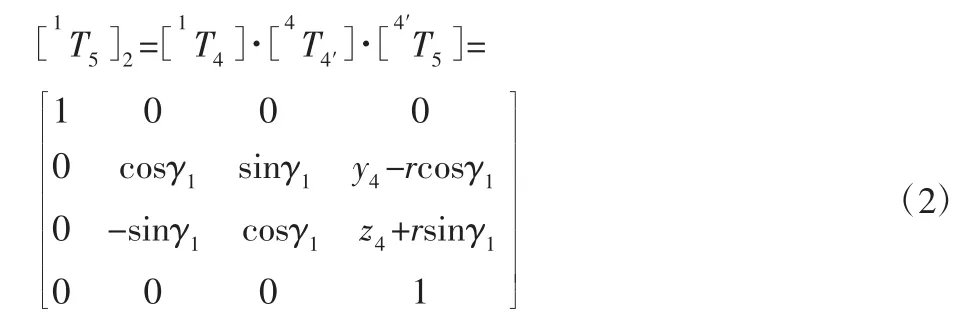
根据式（1）和式（2），由［1T5］1=［1T5］2可得：

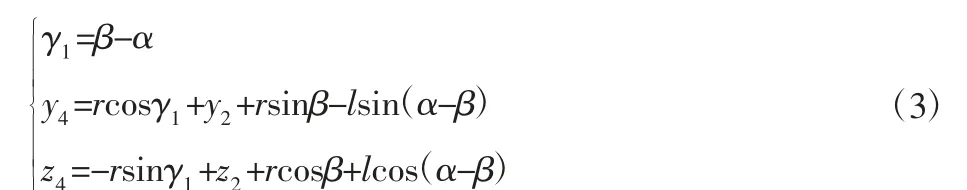
二次曲面子午截面曲线方程[16]为：

式中：ρ—曲线顶点的曲率半径；e2—曲线的偏心率平方。

因此，曲线上点O2和点O4的坐标满足：

由于直线l0为双曲线上过点O2的切线，由式（7）可推导出其斜率k0为：

根据式（8）和图2（a）中角β 的几何意义，可得：

在式（3）、式（5）、式（6）和式（9）中，共有6 个方程，而未知量有11 个，分别为ρ、α、β、γ1、e、y2、z2、y4、z4、r、l。当刀具和工件参数以及加工姿态确定时，r、ρ、e、α 为常量，此时有7 个未知量。因此，可明确β、γ1、l、y2、z2、y4、z4之间的函数关系。

2.2 刀具左倾

与2.1 部分的推导方法相同，当刀具向左侧倾斜时可得如下六个方程：

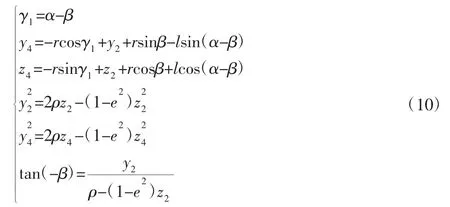
3 双曲面加工的最大口径和最大矢高

由文献[15]中的图3 可知，直线l0的斜率k0存在一个极限值k0max。当k2大于k0max的时候，干涉现象不会发生，而当k2小于k0max的时候，干涉现象可能发生。因此需要先找到k2=k0max的切削点位置。

3.1 k2=k0max时的切削点位置

由文献[15]中的式（5）、式（6）、式（7）和式（10）可得：

根据式（12），可推导出加工不同偏心率的双曲面时，切削点y2与切削角α 之间的映射关系，如图3 所示。

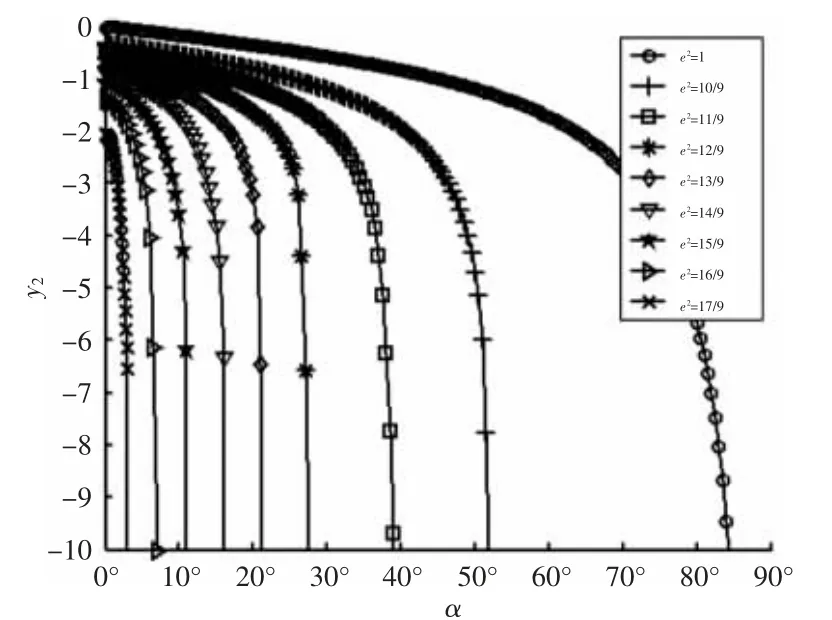
图3 y2-α 曲线Fig.3 The y2-α Curve

3.2 右倾时双曲面最大口径和最大矢高

整理式（3）可得：

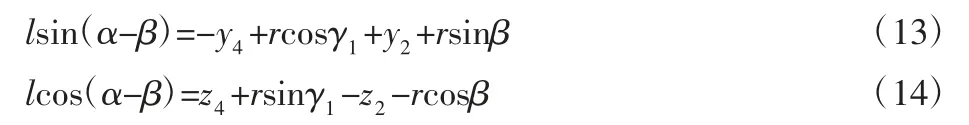
将式（13）和式（14）作比，可得：

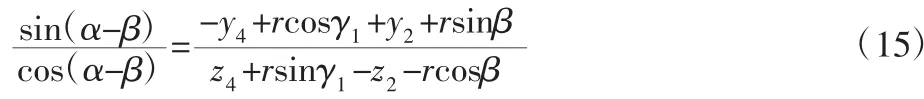
整理得：

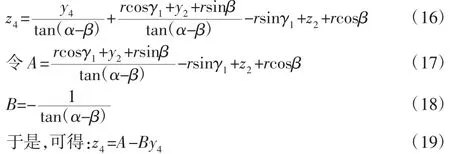
将式（19）带入式（6），可得：

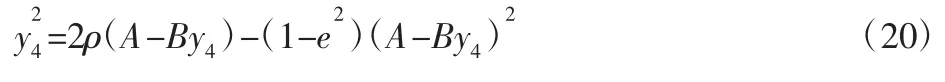
整理式（20）可得：

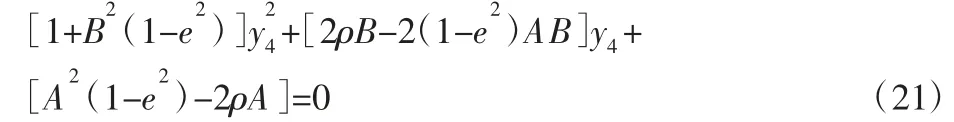
解得：

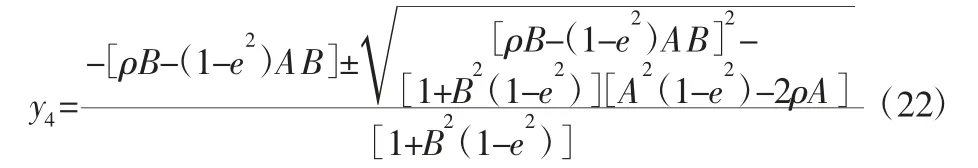
根据式（19）和式（22）可计算出加工不同偏心率的双曲面时，干涉碰撞点O4与切削角α 之间的映射关系。当y4取最小值时，加工双曲面的口径取最大值RR；当z4取最小值时，加工双曲面的矢高取最大值HR。

3.3 刀具左倾时双曲面最大口径和最大矢高

由图2 可知，在刀具左倾的情况下，当加工双曲面底部位置时，干涉碰撞最危险。故当y2取0 时，对应点O4即为要找的那个点，此时的y4对应了加工双曲面口径的最大值RL，而z4对应了加工双曲面矢高的最大值HL。

4 双曲面最大口径和最大矢高

选择不同的刀具，加工不同的双曲面，min｛RR，RL｝和min｛HR，HL｝决定了所能加工的双曲面的最大口径R 和最大矢高H，其变化规律，如图4～图21 所示。

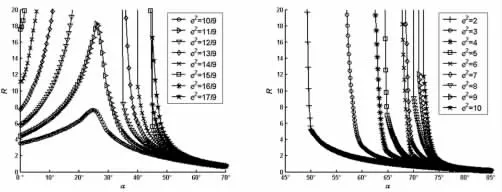
图4 R-α（r=0.2，ρ=1）Fig.4 R-α（r=0.2，ρ=1）

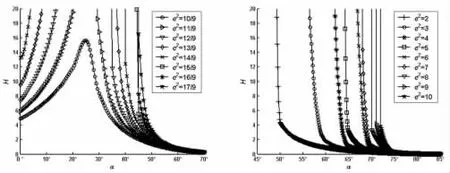
图5 H-α（r=0.2，ρ=1）Fig.5 H-α（r=0.2，ρ=1）

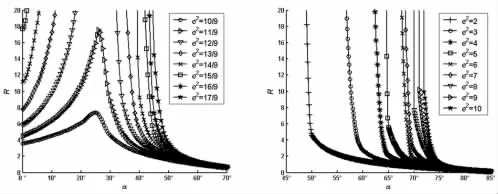
图6 R-α（r=0.5，ρ=1）Fig.6 R-α（r=0.5，ρ=1）

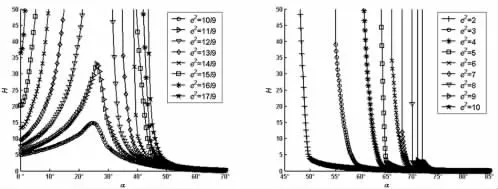
图7 H-α（r=0.5，ρ=1）Fig.7 H-α（r=0.5，ρ=1）

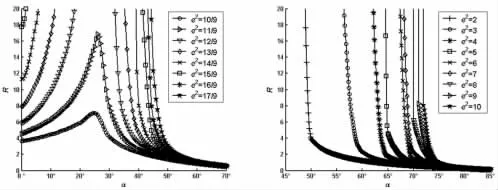
图8 R-α（r=0.8，ρ=1）Fig.8 R-α（r=0.8，ρ=1）

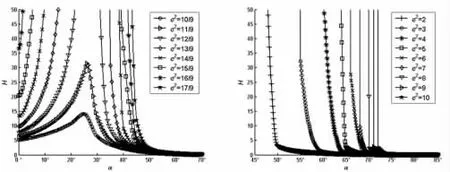
图9 H-α（r=0.8，ρ=1）Fig.9 H-α（r=0.8，ρ=1）

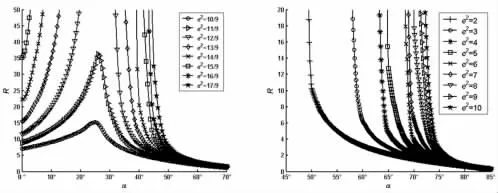
图10 R-α（r=0.5，ρ=2）Fig.10 R-α（r=0.5，ρ=2）

图11 H-α（r=0.5，ρ=2）Fig.11 H-α（r=0.5，ρ=2）

图12 R-α（r=1.0，ρ=2）Fig.12 R-α（r=1.0，ρ=2）

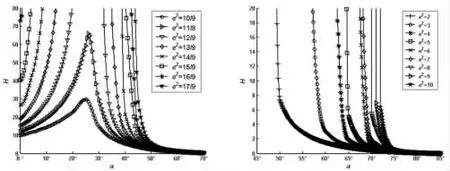
图13 H-α（r=1.0，ρ=2）Fig.13 H-α（r=1.0，ρ=2）

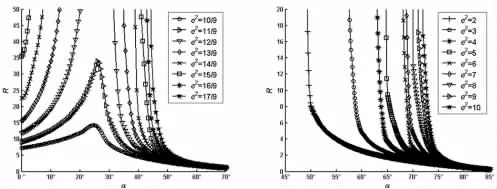
图14 R-α（r=1.5，ρ=2）Fig.14 R-α（r=1.5，ρ=2）

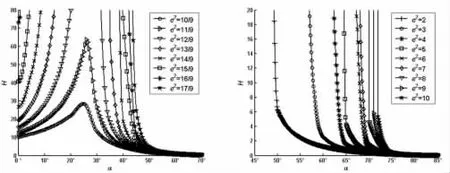
图15 H-α（r=1.5，ρ=2）Fig.15 H-α（r=1.5，ρ=2）

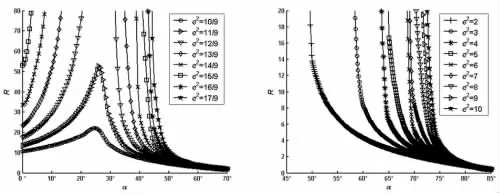
图16 R-α（r=1.5，ρ=3）Fig.16 R-α（r=1.5，ρ=3）

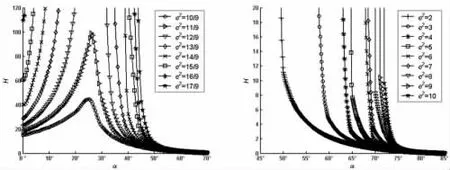
图17 H-α（r=1.5，ρ=3）Fig.17 H-α（r=1.5，ρ=3）

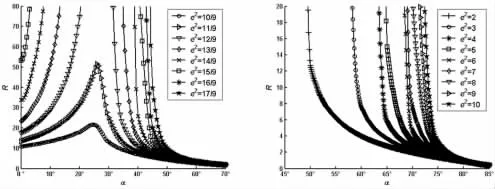
图18 R-α（r=2.0，ρ=3）Fig.18 R-α（r=2.0，ρ=3）

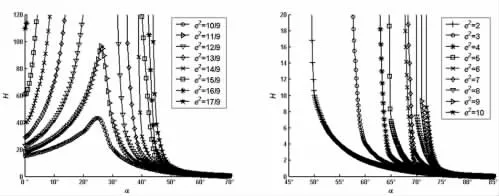
图19 H-α（r=2.0，ρ=3）Fig.19 H-α（r=2.0，ρ=3）

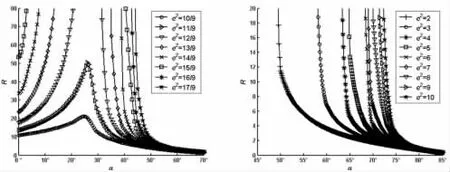
图20 R-α（r=2.5，ρ=3）Fig.20 R-α（r=2.5，ρ=3）

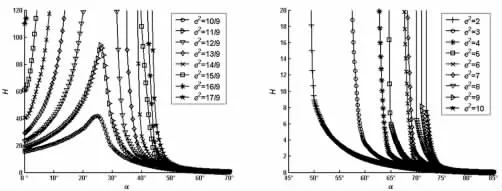
图21 H-α（r=2.5，ρ=3）Fig.21 H-α（r=2.5，ρ=3）

由图4～图21 可知：

（1）如果ρ 取定值，H 和R 均随着r 的增大而逐渐增大；

（2）如果r 取定值，H 和R 均随着ρ 的增大而逐渐增大；

（3）如果ρ 和r 取定值，H 和R 均随着e2的增大而逐渐增大；

（4）如果ρ、r 和e2取定值，H 和R 随着α 的增大而先增大后减小。

5 结论

（1）采用坐标变换方法，建立加工双曲面的数学模型，分析工件参数、刀具参数、刀具切削状态参数以及机床构型参数之间的函数关系。

（2）通过干涉碰撞点与切削角之间的映射关系，推导刀具位于铅垂方向的位置、双曲面最大矢高、最大口径等关键技术指标的变化规律。当干涉碰撞点横坐标取最小值时，加工双曲面的口径取最大值；当干涉碰撞点纵坐标取最小值时，加工双曲面的矢高取最大值。

（3）获得了保证无干涉现象的双曲面加工范围，并分析了其变化规律。当刀具和工件参数不变时，双曲面无干涉加工范围随切削角度的增大而先增大后减小。

（4）由于篇幅所限，对于双曲面无干涉加工范围的实际加工验证与分析等研究成果奖另文发表。