剪切来流下串列三圆柱横向振动响应机理研究

谭潇玲，涂佳黄，雷 平，梁经群，邓旭辉

(1.湘潭大学 土木工程与力学学院，湖南 湘潭 411105；2.中冶长天国际工程有限责任公司，长沙 410205)

实际工程中，当海洋平台、海底管道、桥梁的斜拉索和桥塔等结构物置于流场中时，周围来流的速度往往会随着时间和空间而发生改变，因此，仅限于对均匀来流作用下的流致振动问题进行研究并不足以反映工程当中的实际情况，越来越多的学者将研究的重点放在了非均匀来流作用系统。按照来流性质的不同，非均匀来流可分为周期性来流、Poiseuille管道流以及剪切来流。其中，对于平面剪切来流作用下的结构系统，在任一高度截面圆柱体结构两侧的来流速度由上至下呈现出递减的趋势，从而使得圆柱体结构周围涡量和流体速度分布呈现出较大的差异，速度差的存在引起的压力差会影响结构的表面受力以及运动形式。

通过对平面剪切来流作用下钝体绕流问题进行研究，发现来流剪切率的变化对结构表面的压力系数、升阻力系数、涡脱落频率、边界层分离点的位置以及尾流涡结构等均有较大影响。Kang[1]采用浸泡边界元法对低雷诺数工况下(50≤Re≤160)，单圆柱体结构绕流特性进行了数值模拟。研究发现随着剪切率的增加(0≤K≤0.2)，结构的涡脱落频率和平均升力系数保持不变或者小幅下降，而平均阻力系数则明显增大。但是，Sumner等[2]通过实验研究发现：亚临界雷诺数(4×104≤Re≤9×104)与中低剪切率工况下(0.02≤K≤0.07)，单圆柱体结构的涡脱落频率和平均压力系数随剪切率的增加而增大，但平均阻力系数则减小。另外，结构表面压力的不对称分布使得尾流涡结构的宽度变窄。王伟等[3]对Re=100工况下，剪切率的变化(k≤0.5)对单方柱系统绕流特性的影响进行了分析。研究结果表明，随着剪切率的增加，尾流区域出现的卡门涡街逐渐消失，驻点位置会由最初向高速侧分离点移动后逐渐转变为不再发生变化，而升阻力系数和斯特劳哈尔数的变化趋势在不同的剪切率范围内会呈现出较大的差异。水庆象等[4]对不同剪切率工况下(k=0～0.4)的串列双方柱系统绕流问题进行了数值模拟，研究发现：剪切来流的作用会抑制结构的涡脱落，驻点的位置随剪切率的变化趋势类似于单方柱工况。同时，剪切率的变化会改变串列双方柱间隙流区域水平流速对结构涡脱落的影响。

对于平面剪切来流作用下的涡激振动问题，通过对以往的研究成果进行总结，发现随着剪切率的增大，单圆柱体结构的涡激振动响应主要有以下三个方面的特征：①随着剪切率的持续增大，结构的顺流向最大振幅值最终会远远大于横流向最大振幅值[5]；②结构锁定区间的范围会随着剪切率的增加而扩大[6]；③在流体从均匀来流向平面剪切来流转变的过程中，随结构振动响应的变化，“8”字形运动轨迹的上半部分会逐渐消失，最终呈现为“雨滴”形运动轨迹[6-8]。而对于串列布置多柱体结构系统，随着流场中结构数量的增加，振动响应会更加复杂，这主要是因为除了涡激振动之外，系统的振动机制还有可能出现尾激振动。在尾激振动系统当中，结构的振动响应主要受到上游结构尾流的影响，两种振动机理的共同作用会引起结构更为剧烈的振动响应。目前，对于串列布置多柱体结构群流致振动响应的研究多集中于均匀来流工况。陈威霖等[9-10]对小间距比工况下串列双柱系统的涡激振动问题进行了数值模拟，发现不同于单柱系统，上游圆柱体的振动响应仅存在上端分支。另外，捕捉到T+S和P+S两种尾流模态。基于格子玻尔兹曼方法，Haider等[11]对Re=100时，不同间距比工况下串列双圆柱系统的流致振动响应进行了数值模拟，研究表明：随着间距比的增加，上游圆柱体受到下游结构临近效应的影响，振幅会呈现出“先大于、后小于、再接近于单柱体工况”的变化趋势。而下游圆柱在上游结构尾流涡干扰的影响下，振幅值在大多数间距比工况下均大于单柱体结构。Gao等[12]也考虑了间距比变化对串列三圆柱系统的影响，发现当L/D=2时，上游圆柱的振幅值为单柱体工况的两倍。

本文基于四步半隐式特征线分裂算子有限元方法，对平面剪切来流作用下串列布置三圆柱体结构单自由度流致振动问题进行了数值模拟，重点分析剪切率、雷诺数与折减速度的变化对结构横流向动力响应、流体力系数、相位阶段变化、频率特性与尾流模态等特性的影响，在实际工程中具有一定的参考价值。

1 数值方法及验证

1.1 控制方程

基于任意-拉格朗日欧拉(ALE)描述下的不可压缩黏性流体的N-S方程，其无量纲形表达式为

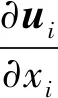
(1)

(2)

式中：t为时间；ui和p分别为流体速度和压力；xi和xj分别为i,j方向的空间坐标；cj=uj-wj，其中cj为流体相对于网格移动速度的对流速度，wj为网格移动速度；雷诺数Re=ρU0D/v，其中U0和D分别为流场特征速度和特征尺寸，v为流体动力黏性系数，ρ为流体密度。

弹性支撑圆柱结构运动体系可假设为质量-阻尼-弹簧系统，考虑双自由度运动的结构控制方程量纲归一化形式为

(3)

(4)

1.2 网格更新

为了防止网格失效，求解Laplace方程得到每个动网格节点位移，其边值问题表达式如下

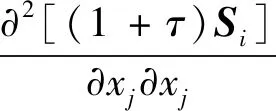
(5)

式中：τ是网格形变控制参数；Si是网格节点i方向位移；gi为运动边界节点位移；Гm是网格动边界；Гf为网格固定边界。

1.3 弱耦合分区算法

采用基于四步半隐式特征线分裂算子的弱耦合分区算法，运用Fortran语言编制相应的数值计算程序求解流固耦合问题，详细的计算框架可参考文献[13]，在此不再赘述。该算法在本课题组以前的工作中已多次验证其能准确地求解钝体结构群涡激振动问题[14]。

1.4 算例验证

将本文计算结果与文献[15]中均匀来流作用下串列布置三圆柱体结构的流致振动响应进行对比来验证本文数值方法的可靠性和适用性。计算模型如图1所示。三圆柱体均仅有横向自由度，圆柱表面速度为u=∂X/∂t,v=∂Y/∂t。无量纲参数设置如下：Re=100，L/D=5，mr=2.0，ξ=0.0。计算域尺寸为[-30D，60D]×[-10D，10D]，上游圆柱(upstream cylinder,UC)、中游圆柱(midstream cylinder,MC)和下游圆柱(downstream cylinder,DC)的圆心位置分别为(-5D，0)，(0，0)与(5D，0)，边界条件设置如下：入口为速度入口：ux=1，uy=0；出口为压力出口：p=0；上下边界为自由滑移边界：∂ux/∂y=0,uy=0；结构表面为无滑移边界：ux=uy=0。将本文计算得出的串列三圆柱体结构的横流向最大振幅值与文献结果进行对比，如图2所示，通过对比发现，计算结果与文献结果的高吻合度验证了本文数值方法的可靠性和适用性。

图1 验证算例计算模型示意图Fig.1 Model schematic of validation case.

图2 串列三圆柱体横流向最大振幅本文结果与文献结果的对比Fig.2 Comparison of the present numerical results of the maximum value of the transverse vibration amplitude(Ymax/D)with existing results

2 问题描述

2.1 计算模型

平面剪切来流作用下串列布置三圆柱体结构流致振动响应的计算模型以及边界条件，如图3所示。三圆柱体仅具有横流向自由度，无量纲参数设置如下：为了深入分析层流范围内(Re<160～210)结构的动力响应以及流体与结构之间的互扰机理，取Re=100和Re=160，由于流体状态较为稳定，可以采用二维模拟进行求解。入口为速度入口：ux=Uc+ky(Uc=1.0),uy=0。由于阻塞率B=0.05，为了保证入口处来流方向一致，剪切率k=0.00，k=0.05，k=0.10。间距比选取L/D=5.5，重点考虑上游结构尾流发展完全后对下游结构振动响应的影响。其他参数为：折减速度Ur=3～21，mr=2.0，忽略结构阻尼的影响，即ξ=0。UC、MC和DC三圆柱体结构的圆心位置分别为(-5.5D，0)、(0，0)和(5.5D，0)。计算域大小与其他边界条件的设置与1.4节中完全一致。

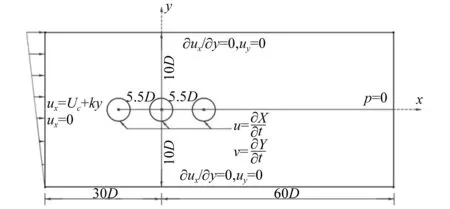
图3 计算模型示意图Fig.3 The schematic diagram of the computational model

2.2 计算参数独立性验证

本文计算域的网格划分采用非结构化的三角形网格，为了更准确地刻画出圆柱周围及尾流区域范围内涡结构的形成和发展，对这两个区域进行网格加密处理，如图4所示。为了确保网格质量，对于单自由度串列布置三圆柱系统，选取Re=100，k=0.1与Ur=7工况对网格数量的变化对结构振动响应的影响进行分析，从而判断哪种类型的网格更适用于求解该问题。由表1可知：该工况下，与粗网格GI相比，随着网格密度的增大，GII工况下三圆柱体结构横流向振幅(Ymax/D)的最大变化为4.40%，而在GIII工况下，最大变化则为4.89%。由于网格数量从GII增大到GIII时，振幅值变化相对较小，且若采用网格GIII进行计算，虽能获得最高的计算精度，但是计算总耗时会大幅增大，计算效率降低。综上所述，本文计算采用的网格密度和分布情况均与GII类似。另一方面，选取该算例，并采用GII网格，分析三种不同时间步长对计算结果的影响，从而判断哪种类型的时间步长对求解该问题更加适用。由表2可知：与Δt=0.005工况相比，随着时间步长的减小，Δt=0.002工况下三圆柱体结构横流向振幅(Ymax/D)和涡脱落频率(St)的最大变化分别为2.41%和4.65%，而在Δt=0.001工况下，最大变化则为2.61%和6.11%。因此，本文无量纲计算步长选取为Δt=0.002。

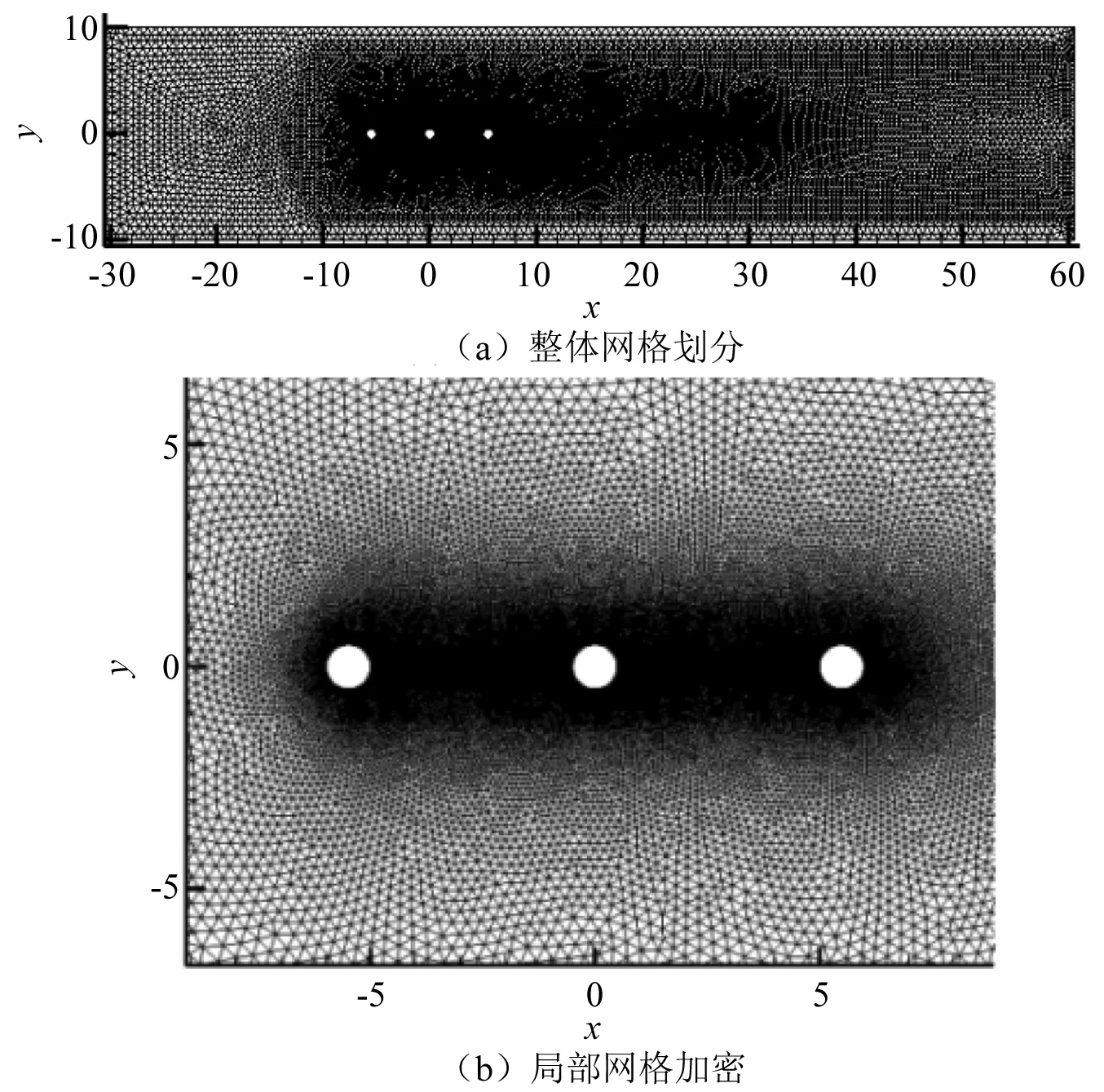
图4 网格划分示意图Fig.4 Schematic of the computational mesh

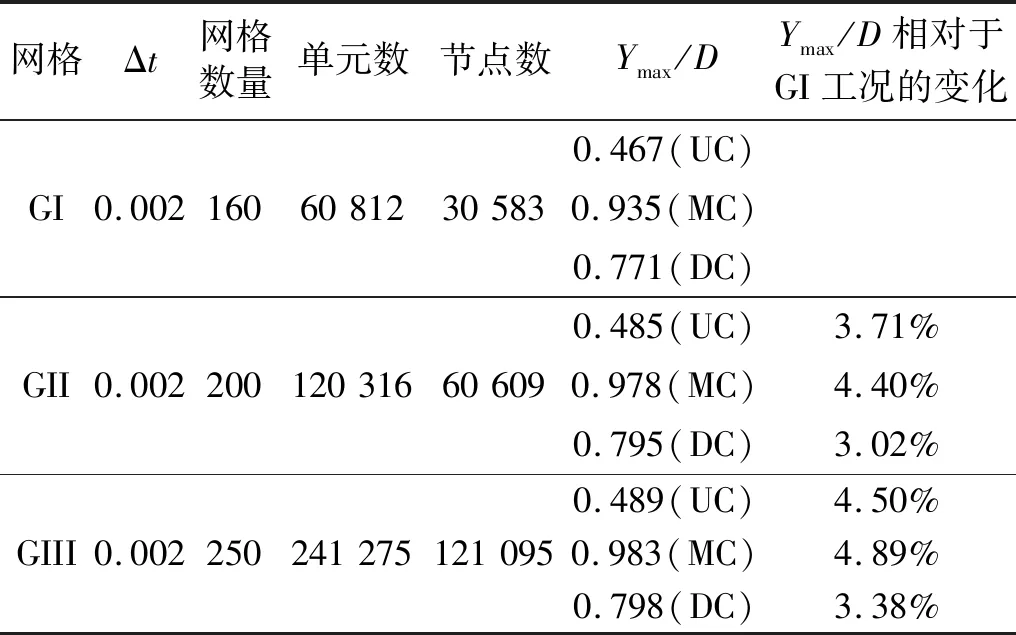
表1 网格独立性验证：串列布置三圆柱单自由度计算结果(Re=100,k=0.10,Ur=7)Tab.1 Grid independence test:the results for the three tandem circular cylinders at Re=100,k=0.10,Ur=7

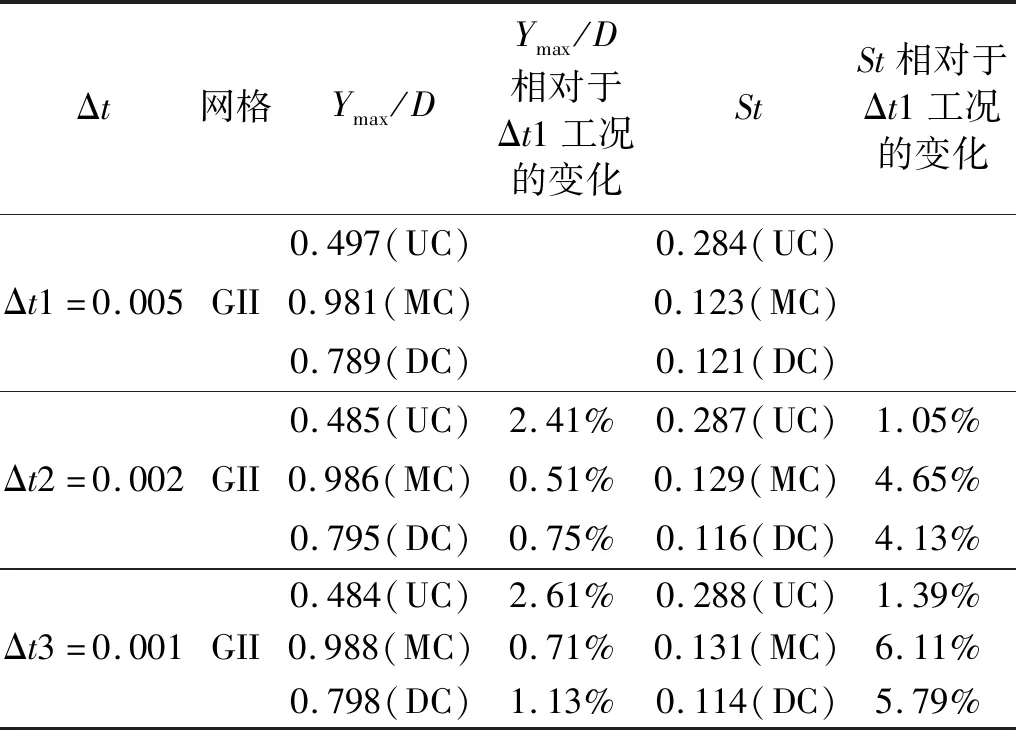
表2 时间步长独立性验证：串列布置三圆柱单自由度计算结果(Re=100,k=0.10,Ur=7)Tab.2 Time-step independence test:the results for the three tandem circular cylinders at Re=100,k=0.10,Ur=7

3 计算结果分析

3.1 动力响应

本节分析了Re=100和Re=160工况下，剪切率和折减速度的变化对串列布置三圆柱体结构横流向动力响应的影响，如图5所示。

由图5可知，不同工况下，三圆柱体结构的振幅曲线均呈现出“先增加后减小再趋于平稳”的变化趋势。根据不同的折减速度范围内剪切率的变化对横流向最大振幅值影响的差异，可将三圆柱体结构的振幅曲线划分为Ⅰ、Ⅱ、Ⅲ和Ⅳ四个区域。对于UC，剪切率的变化对横流向最大振幅的影响普遍较小，在区域Ⅰ(3≤Ur<5)范围内，振幅值随剪切率的增加小幅下降，相反，随折减速度的增加线性增大。在区域Ⅱ～Ⅳ(Ur≥5)范围内，UC横流向最大振幅值随剪切率的增加小幅增大。在Ur=5工况下，振幅曲线取得最大值0.59(k=0.1)，随折减速度的进一步增大，振幅减小并逐渐趋于稳定。对于MC，区域Ⅰ的范围扩大到3≤Ur<8。特别地，Ur=6工况下，剪切率的变化对横流向最大振幅的影响明显增强，k=0.0工况下的最大振幅值达到0.79，超过k=0.1工况(Ymax/D=0.32)振幅值的两倍。与UC不同的是，在经历了区域Ⅱ范围内(8≤Ur<19)横流向振幅随剪切率的增加小幅增大后，MC振幅曲线在区域Ⅳ范围内(Ur≥21)会再次出现随剪切率的增加而减小的情况，且两种变化模式中间存在一个过渡区域Ⅲ(19≤Ur<21)，即振幅不再随着剪切率线性变化。另外，随折减速度的增加，MC横流向最大振幅整体变化趋势与UC基本一致，分别在Ur=7(k=0.00)和Ur=8(k=0.05，k=0.10)工况下达到最大值，最大为1.04(k=0.10)。值得注意的是，Ur=4工况下，结构发生了“弱锁定”现象，对应的横流向振幅出现了极大值。对于DC，根据不同折减速度范围内最大振幅值随剪切率的变化差异所划分出的四个区域的范围进一步发生改变，分别为3≤Ur<10(区域Ⅰ)、10≤Ur<20(区域Ⅱ)、20≤Ur<24(区域Ⅲ)和Ur≥24(区域Ⅳ)。与中上游两圆柱体不同的是，DC的振幅曲线中，在区域Ⅰ范围内部分的折减速度工况下也发现了振幅随剪切率的非线性变化现象。这主要是因为在中上游圆柱尾流的影响下，DC周围旋涡分布会更加复杂，流场的复杂化使得剪切率对DC振动响应的影响发生了改变。不同剪切率工况下，DC振幅曲线的最大值为1.32(k=0.10,Ur=11)。

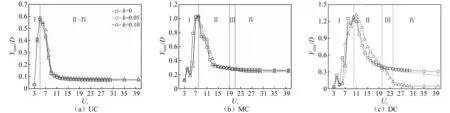
图5 当Re=100时，串列布置三圆柱体结构横流向最大振幅随剪切率和折减速度的变化情况Fig.5 The variation of the maximum crossflow vibrating amplitudes with shear ratio and reduced velocity at Re=100

当Re=160时，随着雷诺数的增大，三圆柱体结构周围流场会逐渐出现三维效应，不稳定性明显增强。流场的复杂化使得中下游两圆柱体的横流向最大振幅值随剪切率的变化情况在不同的折减速度工况下具有较大的差异。与Re=100工况不同的是，三圆柱体结构的最大振幅曲线大致可以划分为随剪切率减小(区域Ⅰ)、增大(区域Ⅱ)以及非线性变化(区域Ⅲ)三个不同的区域，且区域Ⅰ和Ⅱ范围内最大振幅值随剪切率的非线性变化现象出现的频率明显增大，如图6所示。另外，中上游两圆柱体振幅曲线随折减速度的整体变化趋势与振幅峰值均接近于Re=100工况。不同的是，当Re=160时，UC达到峰值以及开始稳定所对应的折减速度减小，意味着流场的变化使得UC发生共振所对应的频率值会增大。与仅受到来流影响的UC不同，中下游两圆柱体周围流场在旋涡脱落影响下的复杂程度远远大于来流，使得中下游两圆柱体振幅难以较快地稳定下来，尤其是k=0.10工况。当中下游两圆柱体的振幅曲线达到峰值后，k=0.10工况所对应结构的振幅值明显大于其他两个剪切率工况，说明雷诺数的增加会对大剪切率工况下结构的动力响应有较大的影响。当k=0.10时，DC分别达到峰值1.54(Ur=12)与1.17(Ur=18)，两个区域中间过渡所对应的极小值点的位置为Ur=17。

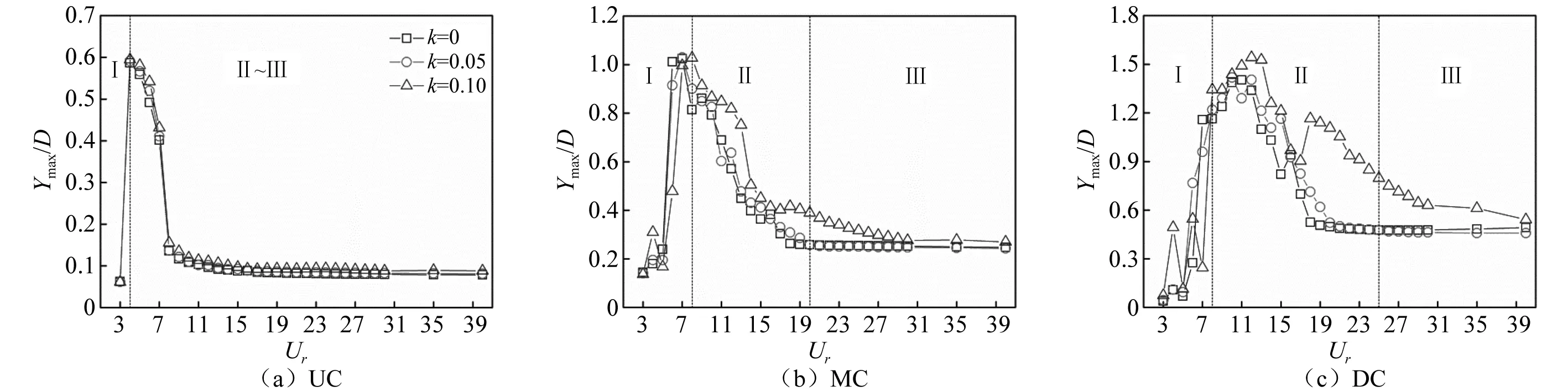
图6 当Re=160时，串列布置三圆柱体结构横流向最大振幅随剪切率和折减速度的变化情况Fig.6 The variation of the maximum crossflow vibrating amplitudes with shear ratio and reduced velocity at Re=160

3.2 柱体表面流体力特性

图7～图10分别给出了Re=100和Re=160工况下，串列布置三圆柱体结构表面阻力系数平均值和升力系数均方根值随剪切率与折减速度的变化情况。

图10 当Re=160时，不同剪切率工况下串列三圆柱体结构升力系数均方根值随折减速度的变化情况Fig.10 The variation of the rms value of the lift coefficient with shear ratio and reduced velocity when Re=160

由图7可知，不同剪切率工况下，三圆柱体结构的阻力系数平均值随折减速度的变化趋势与横流向最大振幅曲线基本一致，均为先增加到最大值后逐渐减小并趋于稳定，且取得峰值所对应的折减速度工况也相当接近。值得注意的是，当结构置于流场中时，会在来流的作用下产生顺流向的推力，而对于串列布置多柱体结构，受到来流影响越大的圆柱所产生的推力就会越大。从图中可以看出，自由来流对三圆柱体结构的作用大小是依次递减的，当Re=100时，中上游两圆柱体的最小阻力系数平均值分别接近于1.00(UC)和0.40(MC)，会大于DC。当Ur=5～6时，部分剪切率工况下，下游圆柱体的阻力系数平均值接近于零，这主要是因为下游圆柱完全处于中上游两圆柱体的尾流中而被屏蔽。另外，随着剪切率的增加，下游圆柱的阻力系数平均值曲线所对应的最大值分别为1.61(k=0.00)，1.21(k=0.05)和0.91(k=0.10)，说明剪切来流作用下流体速度的不均匀分布减小了结构顺流方向所受的流体力。由图8可知，不同剪切率工况下，三圆柱体结构的升力系数均方根值随折减速度的变化曲线呈现出“峰+平台”的变化趋势，且中间存在一个过渡区域Ur=5～8。剪切率的变化对中上游两圆柱体升力系数均方根值的最大值影响较小。而对于下游圆柱，Ur=4工况下，最大值随着剪切率的增加明显减小。在过渡区域内，上游圆柱的升力系数均方根值接近于零，而中下游两圆柱体正处于共振区域内，升力系数的波动性较大，结构的振动较不稳定。剪切率的变化对“平台”范围内上游圆柱升力系数均方根值的影响较小，而中下游两圆柱体的升力系数均方根值则随着剪切率的增加而减小，下游圆柱更为明显，这与其振幅曲线的变化情况基本一致。这可能是因为折减速度较大时，结构刚度较小，流体与结构之间的耦合作用减弱，自由来流对下游圆柱体的影响增强，再加上圆柱表面涡量分布的差异，使得剪切来流作用下下游圆柱的升力系数均方根值会接近于上游圆柱稳定后的数值。

图7 当Re=100时，不同剪切率工况下串列三圆柱体结构阻力系数平均值随折减速度的变化情况Fig.7 The variation of the mean value of the drag coefficient with shear ratio and reducedvelocity when Re=100

图8 当Re=100时，不同剪切率工况下串列三圆柱体结构升力系数均方根值随折减速度的变化情况Fig.8 The variation of the rms value of the lift coefficient with shear ratio and reduced velocity when Re=100

当Re=160时，雷诺数的增大对上游圆柱体升阻力系数的影响较小，而对于中下游圆柱的影响较大，如图9和10所示。由于来流不稳定性增强，中游圆柱最小阻力系数平均值减小50%。而对于下游圆柱，当Ur=4时，与Re=100工况不同，阻力系数平均值仅在k=0.10工况下出现极大值0.84，而在其他剪切率工况下则接近于零，这与振幅曲线的变化基本一致。另外，不同剪切率工况下，下游圆柱阻力系数平均值的最大值有所减小，特别是k=0.05工况，大约减小了20%。当k=0.10,Ur>15时，下游圆柱的阻力系数平均值略微大于其他剪切率工况，这与结构振动的第二个大振幅区域对应。另一方面，k=0.00和k=0.05工况下，下游圆柱的升力系数均方根值峰值的位置转移到了过渡区域范围内且数值明显减小，而k=0.10工况下则恰好相反，与低雷诺数工况相比，最大值增加了37%。另外，不同剪切率工况下，由于下游圆柱产生剧烈振动所对应的区域范围扩大，升力系数均方根值曲线过渡区域的范围扩大到Ur=5～15范围内。值得注意的是，平稳状态的出现均会迟于Re=100工况，且剪切率的变化对升力系数均方根值的显著影响会发生在大折减速度工况。

图9 当Re=160时，不同剪切率工况下串列三圆柱体结构阻力系数平均值随折减速度的变化情况Fig.9 The variation of the mean value of the drag coefficient with shear ratio and reduced velocity when Re=160

3.3 相位阶段变化

图11与图12分别给出了Re=100和Re=160工况下，串列布置三圆柱体结构体系横流向位移和升力系数之间的相位差随剪切率和折减速度的变化情况。柱体结构的力和位移之间相位变化会影响柱体与流场之间能量的传递方式，从而影响结构的振动响应[16]。

由图可知，不同雷诺数和剪切率工况下，三圆柱体结构横流向位移与升力系数之间相位差的变化趋势基本一致：当折减速度较小时，相位差接近于0°，结构会从流体当中获得能量，且随着系统刚度逐渐减小，结构受周围流体的影响增强，从而引起共振现象的发生，激发出较大的振幅。随着折减速度的增加，结构的振动模式发生转变的过程中，相位差会逐渐转变为180°，发生转变所对应的工况称为“相位开关”。当Re=100时，不同剪切率工况下，三圆柱体结构“相位开关”所对应的位置均为Ur=6工况，流场的不稳定性以及剪切率的变化会对相位的转变过程产生较大的影响，中游圆柱体力和位移之间的相位差从0°完全转变为180°所对应折减速度的范围明显扩大，如图11所示。而对于下游圆柱，影响则更为显著，相位差随折减速度的变化曲线波动性较大，力和位移的相位关系在结构不规则运动的过程中会发生显著变化，使得大折减速度工况下，难以快速转变为完全反相的状态，且这种现象随着剪切率的增大愈加明显。当Re=160时，上游圆柱以及均匀来流作用下下游圆柱的“相位开关”提前至Ur=5工况，如图12所示。剪切率的变化对中游圆柱相位差的影响增强，Ur≥8范围内，相位差随折减速度的变化曲线会呈现出下凹趋势，且下凹的幅度以及范围会随剪切率的增加而增大。相反，与Re=100工况相比，下游圆柱的相位关系受剪切率的影响减小。

图11 当Re=100时，不同剪切率工况下串列三圆柱体结构横流向位移与升力系数相位差随折减速度的变化情况Fig.11 The variation of the phase difference between the crossflow displacement and the lift coefficient with shear ratio and reduced velocity when Re=100

图12 当Re=160时，不同剪切率工况下串列三圆柱体结构横流向位移与升力系数相位差随折减速度的变化情况Fig.12 The variation of the phase difference between the crossflow displacement and the lift coefficient with shear ratio and reduced velocity when Re=160

3.4 频谱特性

图13与图14选取了Re=100和Re=160时，部分工况下中下游两圆柱体横流向位移能量谱密度(power spectral density,PSD)曲线的变化情况。在结构横流向位移的PSD曲线当中，振动频率的阶数越高，结构的振动响应就会越复杂，主频所对应的能量越大，结构的振动越剧烈。

由图13(a)可知，当Re=100时，均匀来流作用下，中下游两圆柱体振动位移所对应的PSD曲线随折减速度的变化趋势和3.1小节结构的振动响应一一对应。随折减速度的增加，中游圆柱体的PSD曲线中主频的大小基本一致，且振动主频所对应的能量在共振区间内明显增大。而下游圆柱的主频则随Ur增加逐渐减小，且共振区间内次频的数量明显增大。当Ur=3时，结构的动力响应较弱，PSD曲线中仅出现一个振动频率，且对应的能量较小。随Ur增加，次频数量的增多以及主频能量的增大使得结构的振动出现“调制周期”、不规则振动等不同的模式，动力响应更加剧烈。当中下游两圆柱体的振动响应随折减速度的变化曲线处于下降段时，PSD曲线中次频的数量以及主频所对应的能量值也随之减小。大振幅区域内，下游圆柱主频所对应的能量值明显大于中游圆柱，与两圆柱体最大振幅值对应，如图5所示。剪切来流作用时，部分折减速度工况下，两圆柱体均会出现一个数值接近于零的振动频率，且当Ur=20和Ur=40时，该频率所对应的能量值相当大，但由于频率值较小，对于结构振动响应的影响可以忽略不计，如图13(b)所示。

图13 当Re=100时，不同剪切率工况下中下游两圆柱体结构横流向位移能量谱密度随折减速度的变化情况Fig.13 The variation of the power spectral density of the crossflow displacement with shear ratio and reduced velocity when Re=100

当Re=160时，均匀来流作用下，除了Ur=12工况外，其他折减速度工况下中游圆柱所对应的振动主频均略微大于Re=100工况，如图14(a)所示。而当Ur=12时，会出现两个能量接近的频率值。对于下游圆柱，Ur=12工况下结构振动主频所对应的能量值由0.8(Re=100)增加到1.0(Re=160)。剪切来流作用下，中下游两圆柱体横流向位移PSD曲线对应的主频均减小，如图14(b)所示。另外，大振幅区间内下游圆柱体PSD曲线中出现复杂的“多频”现象，会影响能量在流体与结构之间的传递，从而改变结构的振动特性。

图14 当Re=160时，不同剪切率工况下中下游两圆柱体结构横流向位移能量谱密度随折减速度的变化情况Fig.14 The variation of the power spectral density of the crossflow displacement with shear ratio and reduced velocity when Re=160

3.5 尾流模态

图15和图16分别给出了Re=100和Re=160时，部分工况下三圆柱体结构群尾流场瞬时涡量图，所对应的时刻均为下游圆柱最大正位移处。由图可知，剪切率的变化对三圆柱体结构上下两侧尾流的分布影响较大。当Re=100时，均匀来流作用下，周围流场强弱分布的差异较小，尾流场的旋涡分布相对来说较为规则。而剪切来流作用下，柱体表面自由来流的速度由上至下逐渐减小，使得三圆柱体结构上表面的旋涡明显强于下表面，下侧旋涡在向尾流区域发展的过程中受到上侧涡流的挤压、结构的运动以及流体之间惯性力的影响较大，在尾流场的分布会呈现出较大的不规则性，如图15所示。尾流模态随折减速度的具体变化过程如下：均匀来流作用下，当Ur=3时，结构振动较为稳定，尾流模态呈现为标准的双行2S模式(S：单涡)。当Ur=5时，上游圆柱的振幅增大，2S模态的横流向间距也随之增大，中上游两圆柱体尾流对下游圆柱的“屏蔽”作用进一步增强，周围流场速度的减小使得结构的横向流体力减小，从而减弱振动幅度Ymax/D=0，如图5(c)所示。随折减速度进一步增大，脱落旋涡与结构之间的耦合作用增强，中下游两圆柱逐渐激发出大幅振动。特别是当Ur=7时，中游圆柱的振幅达到峰值，其上下表面脱落的旋涡受到结构强烈的摆动作用而明显加长，从而正面撞击下游圆柱并在其上下两侧分裂成一大一小两个子旋涡，在下游圆柱表面形成一对相反的作用力，使得结构表面升力系数接近于零，振动幅度减弱，如图8(c)所示。当Ur≥9时，结构尾流场呈现为规则的2S模态，且随着结构振动响应逐渐减小而趋于稳定，涡街的横向间距以及旋涡数量明显减小。另外，下游圆柱周围涡街的分布均呈现为中上游圆柱下表面脱落的旋涡恰好或即将到达下游圆柱下表面，而上侧旋涡即将脱落的形式，但是四种折减速度工况下下游圆柱的振动幅度却有较大的差异，这主要是旋涡在下游圆柱表面所产生的压力区的强弱差异造成的。剪切来流作用下，大多数折减速度工况下，由于下侧旋涡强度较弱且距离较远，下游圆柱的运动主要受到上侧涡流的影响。当Ur=3和Ur=5时，三圆柱体结构尾流模态呈现为上下两侧涡量差异较大的2S模态，由于旋涡的强度以及脱涡频率较大，上侧涡流在向远尾流区域发展的过程中随着能量的耗散会出现涡量堆积的现象。另外，中上游两圆柱体对下游圆柱的“屏蔽”作用会持续至Ur=6工况。结构产生大振幅响应所对应的折减速度区域内，尾流场旋涡强度较大且分布的不规则性进一步增强。值得注意的是，当Ur=11时，中下游两圆柱体周围涡流的数量明显增大，在MC尾流区呈现出P+S模态(P：对涡)。同时，耦合作用的变化使得柱体上下两侧涡量差减小，引起DC发生剧烈的振动响应Ymax/D=1.32，如图5(c)所示。随着折减速度的进一步增大，到Ur=40时，中游圆柱与周围旋涡的耦合作用与均匀来流工况类似，然而下游圆柱却有很大的差异，尾流模态类似于Ur=5工况，使得下游圆柱的振幅逐渐趋近于零，远小于k=0.00工况。

图15 当Re=100时，不同剪切率工况下串列三圆柱体结构瞬时涡量图随折减速度的变化情况Fig.15 The variation of the instantaneous vorticity contourswith shear ratio and reduced velocity when Re=100

当Re=160时，流场的复杂化使得尾流分布以及向远尾流区域发展过程当中的不规则性、涡流的数量和强度明显增强，如图16所示。最显著的变化就是受到结构运动与惯性力的影响，流场当中大部分旋涡的长度增大，发生分裂之后会导致近尾流区域分布较多的强度较弱的子旋涡。均匀来流作用下，当Ur=3和Ur=5时，中下游圆柱的尾流模态均呈现出2S模式，但涡街向下游发展的过程中有发生偏斜且转变为交替分布、间隔较远的双行涡街的趋势。当Ur=6时，中游圆柱的振动幅度明显大于Re=100工况，尾流区域涡街的横向间距增大。随折减速度的进一步增大，雷诺数的增大改变了三圆柱体结构运动与旋涡脱落之间的关系，从而改变结构周围旋涡和压力区的分布。当Ur=9和Ur=18时，中游圆柱尾流区均出现了P+S旋涡模态，但对下游圆柱的影响有所不同，其横向振幅相差近两倍，即Ymax/D=1.17(Ur=9)与Ymax/D=0.43(Ur=18)。剪切来流作用下，当Ur=3时，下游圆柱体尾流区域的旋涡在较大的惯性力的影响下难以维持2S模态，在近尾流区域呈现为不规则的分布。当Ur=5时，上下两侧涡流的横向间距进一步增大，这主要是因为下侧强度较弱的涡流发生偏斜，与均匀来流工况下仅受到结构振幅的影响不同。值得注意的是，当Ur=18时，中游圆柱的尾流会从下游圆柱上下两侧通过，有利于其表面旋涡的发展，从而加剧结构的振动，形成了第二个峰值，如图6(c)所示。其余折减速度工况下，尾流区域旋涡的分布则更加的不规则。

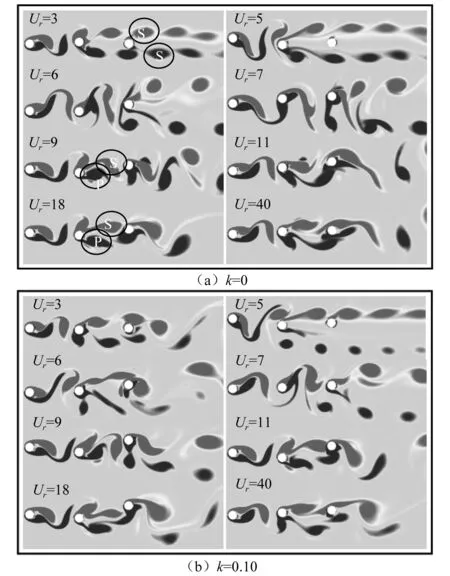
图16 当Re=160时，不同剪切率工况下串列三圆柱体结构瞬时涡量图随折减速度的变化情况Fig.16 The variation of the instantaneous vorticity contourswith shear ratio and reduced velocity when Re=160

4 结 论

基于四步半隐式特征线分裂算子有限元方法，本文对平面剪切来流作用下串列布置三圆柱体结构的单自由度流致振动响应进行了数值模拟，深入探讨了雷诺数、剪切率与折减速度的变化对结构群横流向动力响应、流体力系数、相位特征、频谱特性与尾流模态的影响，阐释了流体与结构群之间的耦合效应，得到的主要结论如下：

(1)雷诺数的增加对大剪切率工况下结构的振幅响应有明显的促进作用。不同的雷诺数工况下，三圆柱体结构的振幅曲线随剪切率呈阶段性变化，最大振幅值会随剪切率的增加而小幅增大。

(2)雷诺数和剪切率的变化对下游圆柱的影响大于中上游两圆柱体。随雷诺数的增加，下游圆柱体在部分剪切率工况下升阻力系数的最大值及其对应的位置会发生明显的改变。剪切率的变化对下游圆柱体共振区间内的升阻力系数以及大折减速度范围内的升力系数均方根随剪切率变化的波动性较大。

(3)随着雷诺数和剪切率的增加，中下游两圆柱体发生相位转变所对应的区域范围明显扩大。值得注意的是，由于中下游两圆柱体在整个振动周期内相位变化的差异较大，使得大多数工况下两圆柱体的相位差不会呈现出完全同相或反相的状态。

(4)雷诺数和剪切率的增大会显著增大横流向位移能量谱密度曲线中频率的阶数，从而影响能量在流体与结构之间的传递，改变结构群的动力响应。

(5)三圆柱体结构尾流场的旋涡分布随折减速度变化规律性较强，主要会出现2S与P+S等尾流模态。但随雷诺数和剪切率的增加，尾流场的旋涡分布在较大的惯性力以及来流速度差的影响下变得更加复杂。