基于全箭振型数据的大型捆绑火箭模态筛选与对齐方法

胡明明，谭述君,2，周如好，何 骁

(1.大连理工大学 航空航天学院，辽宁 大连 116023；2.辽宁省空天飞行器前沿技术重点实验室，辽宁 大连 116023；3.上海航天控制技术研究所，上海 201109)

随着科技的不断发展，空间技术是每一个大国争相发展的技术。而运载火箭是人类进入空间的最主要手段[1]。考察国内外同类捆绑火箭,如大力神-ⅢC[2]、土星V[3]、航天飞机[4]、阿里安-4[5],CZ-2E[6]、长征五号[7]等，可以看出随着火箭的大型化、长助推化发展，捆绑火箭弯、扭、纵耦合严重，形成十分复杂的模态族[8]。同时，运载火箭在飞行过程中随着燃料的消耗，弹性模态也不断变化，甚至会出现模态跳跃和消失的现象[9]，从而给运载火箭动力学建模和控制带来极大的困难。因此提出大型捆绑火箭有效的模态筛选和对齐方法是非常必要的。

常用的模态筛选方法有模态有效质量法[10]和能量分数法[11]等等。Chung等[11]还提出了模态有效质量和能量分数相结合的方法，以便将整体和局部模态都包括在内。模态百分比法[12]则是在所考虑的激励频率范围内量化模态相对重要性的方法[13]。Mercer等[14]对以上方法作了对比评估，并分析了其工程价值。传统的运载火箭模态筛选方法一般仅利用头部单点的模态数据进行模态筛选。运载火箭则提出了平方根位移法}，该方法易于受到特定位置或特定点选取的影响。对于捆绑火箭的复杂模态，单纯利用某一点或特定位置的振型数据已很难区分，因此有必要利用全箭振型数据进行模态筛选。吴胜宝等[16]公布了一种大型液体捆绑火箭复杂模态辨识方法。王勇[17]提出一种基于火箭芯级振型数据的模态筛选方法，提高了模态筛选的正确性，然而对某些助推器局部模态未能很好的筛选出来，并且该方法在归一化操作中没有区分振型数据的横向位移和角位移量纲的不同。

传统的模态对齐方法一般是按照频率的大小进行对齐，如邓舞燕[18]提出的模态对齐思路，然而从本质上来说模态对齐应该是模态形状的对齐，而模态形状和模态频率之间并没有必然的联系。Allemang等[19]提出了一种基于模态置信度准则(MAC)的模态快速自动排列技术。该方法使用了模态振型数据，提高了模态对齐的准确性，但是模态置信度准则只是按照相似度值来对齐，可能导致不同的模态类型的对齐，并且还可能导致出现某一阶次同时和好几个阶次对齐的问题。

本文充分利用芯级和助推器的振型数据，改进了模态振型数据的归一化方式，提出了弯曲模态、扭转模态、纵振模态及局部模态等的模态筛选系数公式。并改进了基于振型数据的模态置信度准则的对齐方法，从而实现大型捆绑运载火箭的模态筛选和对齐。最后，在某型号运载火箭时变动力学模型上进行了仿真验证。

1 传统的火箭模态筛选方法

传统火箭长细比较小，模态类型较为简单，并且纵横扭耦合不严重，因此一般通过头部点(一般是火箭的理论尖点)振型数据来判断模态类型。例如某工业部门进行某构型火箭姿控系统设计时曾使用一种单点法的模态筛选方法[17]。该方法首先取该时刻各模态头部点(一般是火箭的理论尖点)振型数据的6个分量值[UXUYUZRXRYRZ]T，按照最大值归一化。然后计算模态分量UY/UZ，RX，UX的值进行模态筛选，结果如下：

(1)UY/UZ=1时，为45°(或-13.5° )方向的弯曲模态。

(2)UY/UZ=-1时，为45°(或135° )方向的弯曲模态。

(3)RX=1时，为扭转模态。

(4)UX=1时，为局部模态。

该技术经过仿真验证，对于传统火箭具有很好的可行性和工程价值。但其仅利用头部点振型数据对模态进行筛选，没有充分利用模态振型数据，因此，对大型捆绑火箭的复杂模态形状的判别不够准确，本文将发展基于全箭振型数据的模态筛选方法。

2 基于全箭振型数据的模态筛选方法

大型捆绑运载火箭长细比较大，纵横扭耦合严重，导致其模态十分复杂。并且火箭的模态类型是由火箭整体模态振型数据来体现的，仅仅使用模态头部点是不够的。本节在王勇的基础上，首先充分利用芯级和助推器振型数据提出了模态类型的精细化定义，然后对模态振型数据归一化方式和弯曲、扭转、纵振的筛选系数公式做出了改进，从而建立了适应大型捆绑火箭的新的模态筛选方法。

2.1 模态类型的定义

对于大型捆绑火箭，助推器的长细比也越来越大，导致助推器的模态振型成为构成整个箭体模态振型的重要组成部分，不宜忽略。因此，利用芯级和助推器振型数据分别对芯级和助推器进行模态筛选，得到的模态筛选结果如下表 1所示。这样的分类可以很好的将捆绑火箭的整体振型特征和耦合模态描述出来。其中XJ表示芯级,ZT表示助推器，XJ弯ZT弯表示芯级是弯曲模态且助推器是弯曲模态，以此类比。

表1 模态类型组合Tab.1 Combination of modal types

2.2 振型数据归一化处理

分别对芯级和助推器进行振型数据归一化处理，令其全部站点x，y，z的归一化位移平方和为：

(1)

令全部站点y横向的归一化位移平方和为：

(2)

令全部站点x，y，z的归一化转角平方和为：

(3)

令全部站点x的归一化转角平方和为：

(4)

同理Siz、Six、Siry和Sirz也是类似定义。

2.3 模态类型的表征

对于弯曲模态来说，其y方向和z方向的模态位移较大，因此弯曲模态的表征系数如下：

(5)

对于纵振模态来说，其x方向的模态位移较大，故纵振模态的表征系数如下：

(6)

而对于扭转模态来说，其绕x方向的转角位移较大，由此，扭转模态的筛选公式使用转角数据。扭转模态表征系数如下：

(7)

同时，对于弯曲模态来说，其绕y和z轴的转角位移较大，因此也可以采用转角数据进行检验，公式如下：

(8)

此时，若为弯曲模态，则由转角计算出的ηr也是接近于1。

对于弯曲模态，进一步可以将其分为俯仰和偏航。其中俯仰或偏航模态类型表征系数计算公式如下：

(9)

其中当ξ>1时，为俯仰模态，反之为偏航模态。

根据计算出的模态类型表征系数，找出最大值，那么该最大值所属的模态类型即为当前阶次的模态类型。

最后对于局部模态的判断，引入一个比重系数λ，定义如下：

λ1是芯级比重的系数，由芯级所有数据平方和平均后，再开根号。n1为芯级站点个数，Si,xj是芯级所有站点位移平方加和，表达式为

(10)

(11)

λ2是助推器比重系数，Si,zt是助推器所有站点位移平方加和，其定义也是类似Si,xj，n2是助推器个数，同理：

(12)

(13)

当λ≥100%时，表示芯级变形为主；反之助推器变形为主。此时助推器的数据，按照一个助推器或者多个，对于芯级比重判别几乎没有影响。

3 不同秒点的模态对齐方法

(14)

MAC值介于之间，MAC值越大，模态越相似。模态置信度与模态本身幅值大小无关，只与模态本身形状有关，因此不受模态归一化方式的影响。

然而，由于大型捆绑运载火箭模态振型的复杂性，仅利用模态置信度准则可能导致不同的模态类型进行了对齐，并且还有可能导致某一阶次重复性对齐，使得模态数据难以对齐。对此，本文先进行模态筛选，然后结合模态筛选结果，利用模态置信度准则完成不同秒点的对齐。具体步骤如下：①对所有秒点进行模态筛选，按模态类型进行分类；②对于每一类型模态的集合，分别利用MAC准则去下一个秒点的对应类型的模态集合里进行对齐；③将已对齐的阶次进行跳过，得到该模态类型的所有对齐的结果；④将遗漏的阶次去下一个秒点剩下的所有阶次里进行对齐，直到所有的阶次都对齐为止。例如第0 s的俯仰弯曲模态类型，先从下一个秒点的俯仰弯曲模态集里找到与其对齐的阶次，最后将第0 s遗漏的未对齐的阶次按照置信度准则从下一个秒点剩下的阶次中找对齐即可。

4 仿真验证

采用本文提出的模态筛选、对齐方法，利用某型号大型捆绑火箭模态振型数据，完成了该火箭动力学模型的模态筛选和对齐，并与模态振型图进行对比，来验证本文方法的有效性。进一步将模态筛选和对齐结果在某型号捆绑火箭姿态控制系统模型上进行了仿真验证。

4.1 模态筛选方法的验证

使用某型号捆绑火箭的模态振型数据进行模态筛选，以该火箭第5 s的振型数据为例，其模态筛选结果如表 2所示。表中第6列为综合后的模态筛选结果，分别为芯级变形为主的整体俯仰弯曲、偏航弯曲、扭转和纵振模态，以及助推变形为主的局部模态。同时给出了芯级、助推器模态类型及芯级占全箭比重等信息。表中筛选的俯仰弯曲模态和偏航弯曲模态的频率相互对应，也从侧面验证了筛选结果的正确性。

为了验证表 2的筛选结果，将第5 s的前30阶模态振型图画出。图 1分别给出了第1、2、6、12、22、30阶的振型图，可以看出它们分别是偏航弯曲、俯仰弯曲、局部助推弯曲、扭转、纵振和俯仰弯曲模态，这与表 2筛选结果一致，验证了本文筛选方法的正确性。值得说明的是，图 1中第30阶的俯仰弯曲模态体现的是火箭头部局部变形，这一点本文方法并没有刻画出来。

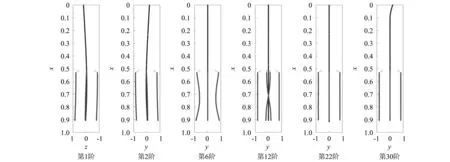
图1 部分阶次振型图Fig.1 Partial order mode shape diagram

表2 第5 s时刻前30阶模态筛选结果表Tab.2 The first 30 orders results of modal selection at the 5th second

4.2 模态对齐方法的验证

将第0 s的模态筛选结果，按照弯曲(俯仰弯曲和偏航弯曲)、扭转、纵振、局部模态依次排列，然后利用本文方法对后续秒点进行模态对齐。限于篇幅，表 3列出了弯曲(5阶)、扭转(2阶)、纵振(1阶)、局部模态(2阶)的对齐结果。从表中给出模态类型可以看出第0 s、第5 s、第35 s的阶次完全对齐，第125 s的对齐结果中只有第20阶(模态类型是局部模态)与前面的秒点阶次(模态类型是俯仰弯曲)没有对齐，产生偏差的原因可能是由于时间间隔过大，导致没有十分匹配的阶次与其相对应，这也提示在模态对齐时秒点间隔不能太大。

为验证表 3的对齐结果，将不同秒点对齐结果的振型图画出。限于篇幅，仅给出第0 s的第1阶的对齐结果图，如图2所示。通过振型图可以看出，不同秒点的振型图非常接近，对齐结果正确。

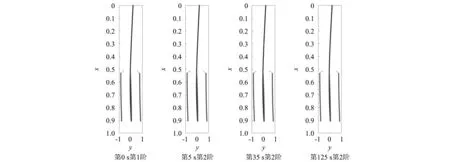
图2 第0 s的第1阶的对齐结果图Fig.2 Alignment result of the 1st order of the 0th second

表3 4个秒点的模态对齐结果表Tab.3 4 seconds modal alignment result table

4.3 姿控系统模型的仿真验证

运载火箭在飞行过程中的燃料消耗导致其模型是时变的，不同秒点的模态振型变化较大，同时随着火箭柔性的增加，仿真模型中需要保留更高阶的模态。如果模态筛选、对齐出现问题，将会导致仿真结果不合理、甚至发散终止。因此本文利用上面对该火箭的模态筛选、对齐结果，建立运载火箭的时变刚-弹姿态动力学模型，在专业仿真平台进行姿控系统的仿真，验证本文模态筛选、对齐方法的正确性。图3～图4给出了偏航通道姿态角和姿态角速度的响应曲线。可以看出，在运载火箭的整个飞行段中，虽然模型是时变的，干扰也是时变的，但是姿态角偏差响应曲线都在1°范围之内，说明所设计的控制系统是稳定的。在60 s和80 s处出现的明显波动，则是因为此处是大风区受较大的切变风干扰。图5～图6给出了对姿态稳定性影响较大的前两阶弹性振动模态的响应曲线，可以看出全箭弹性模态的波动曲线与姿态响应是一致的。上述仿真曲线与传统上采用手动、经验方法进行模态筛选和对齐得到的仿真模型的仿真曲线是一致的，验证了本文提出的模态筛选、对齐方法的正确性。

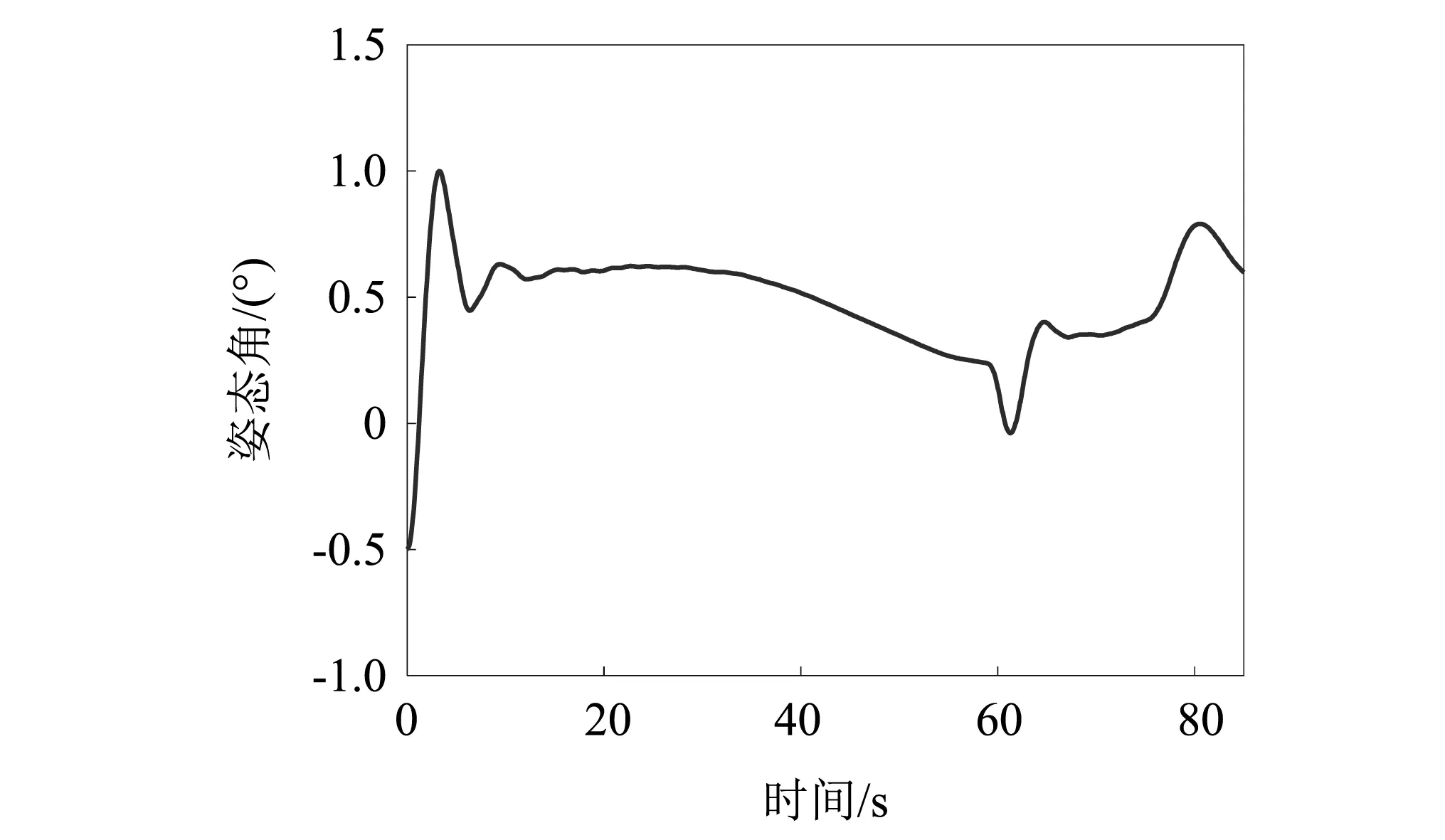
图3 偏航姿态角曲线 Fig.3 The yaw attitude angle curve

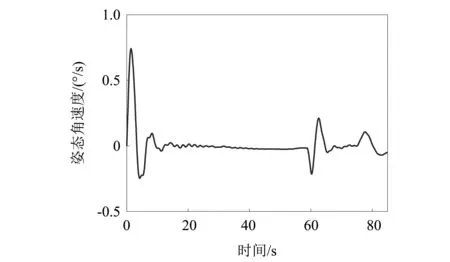
图4 偏航姿态角速度曲线Fig.4 Yaw attitude angular velocity curve

图5 全箭一阶弹性模态Fig.5 Full Rocket First Order Elastic Mode

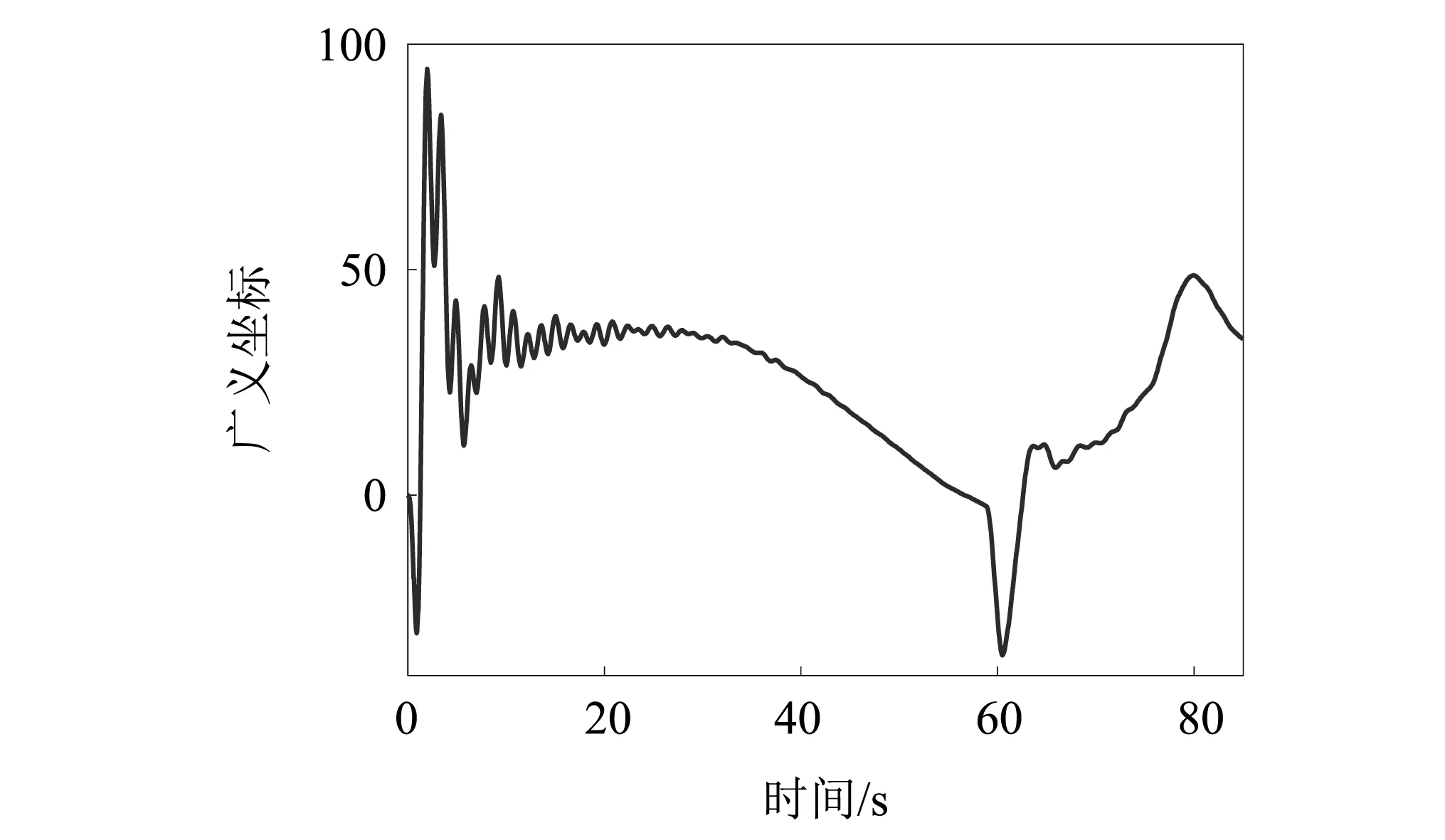
图6 全箭二阶弹性模态Fig.6 Full Rocket Second Order Elastic Mode

5 结 论

本文利用全箭振型数据提出了一种大型捆绑火箭的模态筛选和对齐方法，通过对芯级和助推器单独进行模态筛选，给出了更准确的模态分类，并且定义了一个判别局部模态的系数，将以助推器为主的局部模态很好的筛选了出来。后续通过模态对齐和仿真验证，得到了合理的仿真结果，进一步验证了模态筛选和对齐的准确性，有效的解决了大型捆绑火箭模态复杂带来的建模问题，为后续的复杂动力学仿真和姿态控制系统设计奠定了基础。