组合式剪力键预制拼装桥墩结构及其抗震性能研究

李 辰，江 辉，郭 辉，马馨怡，宋光松

(1.北京交通大学 土木建筑工程学院，北京 100044；2.中国铁道科学研究院 高速铁路轨道技术国家重点实验室，北京 100081；3.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081)

预制拼装桥梁(装配式桥梁)与整体现浇桥梁相比，具有建造速度快、预制构件质量高、施工干扰因素少、施工安全风险小、绿色环保等一系列优点，尤其对于城市桥梁，采用预制拼装结构可有效减少对城市区域既有交通的干扰，降低施工振动与噪声对周围居民的影响。鉴于上述诸多优点，近年来装配式桥梁受到广泛关注，2019年9月我国《交通强国建设纲要》的颁行，为此类桥梁的推广应用带来更加广阔的前景。

相对于上部梁体，预制拼装桥墩的发展时间较短。按抗震性能的不同，可大致将其分为“等同现浇”和“非等同现浇”桥墩两类[1]。“非等同现浇”预制拼装桥墩主要应用于国外，如美国183号国家高速公路高架桥、七英里大桥等。我国杭州湾大桥、港珠澳大桥、上海S6公路、成都羊犀立交等跨海及市政桥梁中均采用“等同现浇”预制拼装桥墩。由于“非等同现浇”预制拼装桥墩节段间接缝构造的存在，桥墩侧向约束较差，其抗震性能可能会弱于整体现浇墩。在工程实践中，通常增加特殊构造措施以增强节段间的连接性能，如新西兰South Rangitikei铁路桥、北京黄徐路跨京台高速高架桥分别在桥墩与承台间采用混凝土方形销和抗剪锚栓以增加桥墩抗剪能力；美国旧金山-奥克兰海湾大桥引桥中采用销栓柔性连接方式可有效削减桥墩与上部结构、承台的弯矩传递。

杜修力等[2]系统总结了摇摆桥墩的抗震研究进展，指出干接缝桥墩在强震下仅依靠界面摩擦传递剪力时，节段可能发生相对滑移。葛继平等[3-4]进行了干接缝节段拼装桥墩的拟静力试验，研究发现试件接缝出现滑移错动的现象，桥墩发生剪切破坏。Li等[5]通过双向振动台试验发现，预制拼装桥墩抗扭刚度不足，动载下节段发生明显扭转。为此，部分学者提出增设剪力键来防止节段滑移、扭转。何铭华等[6]提出多种样式的嵌入式接头，可为预制拼装桥墩提供稳定的横向剪力传递机制。Jiang等[7]、Bu等[8]研究了混凝土剪力键的损伤破坏机理，并回归了剪切强度计算公式。贾俊峰等[9]提出了螺栓连接的机械连接方式，以提高桥墩的抗剪能力和耗能能力。Hung等[10]提出在节段间增加钢销钉或圆柱形混凝土剪力键的半刚性改进方案。Kim[11]发现钢管抗剪连接件可减少装配式桥墩在中等地震下的修复工作量。Zhou等[12]发展了适用于双柱式摇摆墩的钢管剪力键，以限制主梁、基础与墩柱之间的明显滑移。

梳理既有研究成果可发现，“非等同现浇”预制拼装桥墩的研究与应用实践仍处于起步阶段，强震下桥墩仅依靠混凝土界面摩擦力不足以提供足够的剪扭刚度，设置剪力键是提高桥墩抗剪扭能力的有效措施。混凝土剪力键因应力集中可能导致其局部破坏严重，钢剪力键性能比较良好，尽管已在个别工程中应用，但部分构造传力模式复杂，对施工精度要求较高，同时单一剪力键构造无法满足桥墩抗扭需求，因此适用于“非等同现浇”预制拼装桥墩科学可靠、便捷实用的剪力键构造方案还有待深入研究。

本文提出一种组合式钢套筒(销棒)剪力键预制拼装桥墩结构，以某城市桥梁为工程背景，建立考虑多种复杂非线性行为的精细化有限元数值模型，通过拟静力分析和非线性动力分析，讨论了预应力筋及剪力键设计参数对桥墩抗震性能的影响规律，检验了所提出方案的可行性。

1 组合式剪力键预制拼装桥墩结构形式的提出

1.1 既有装配式桥墩拼装结构方案分析

“等同现浇”预制拼装桥墩的连接方式主要包括灌浆套筒连接、灌浆波纹管连接、机械套筒连接和承插式连接等。虽然此类桥墩的力学性能不弱于整体现浇桥墩[13]，但其施工工艺较为复杂，需现场二次浇筑，且节点性能对灌浆料强度、浇筑密实性的依赖程度较高，灌浆质量检测困难[14]。因此，本文暂不讨论“等同现浇”预制拼装桥墩，下文提及的预制拼装桥墩均指“非等同现浇”桥墩。

“非等同现浇”预制拼装桥墩的抗剪连接方案主要包括混凝土剪力键和钢剪力键。不同类型剪力键的优缺点对比见表1，可发现，混凝土剪力键由于应力集中易于出现严重损伤，既有的钢剪力键或者对施工精度要求高，或者地震后容易产生较大塑性变形，或者构造复杂且处于理论研究阶段，发展一种构造简单、稳定可靠、抗剪扭强度高的剪力键具有重要意义。

表1 不同类型剪力键优缺点对比Tab.1 Comparison of different shear keys

1.2 新型预制拼装桥墩结构方案的提出

本文充分利用钢材抗剪强度高、传力均匀且具有较强变形能力的特点，提出一种组合式钢套筒(销棒)剪力键，其构造形式如图1所示。该剪力键由组合式空心钢套筒剪力键(内外钢管)和实心钢销棒剪力键(外钢管+内钢销棒)组成，具有以下特点：①可有效提高桥墩抗剪能力，抑制侧向滑移；②对称分散布置的多组钢销棒剪力键可提供可靠的抗扭能力，避免桥墩扭转；③钢套筒可兼作预应力筋孔道，方便施工；④所有构件采用热镀锌技术防腐，混凝土截面边缘设置防水密封圈以提高结构的耐久性。

图1 组合式钢套筒(销棒)剪力键构造图Fig.1 Structural diagram of the combined steel sleeve (dowel)shear keys

结合上述组合式剪力键，本文以某城市桥梁为工程背景，设计相应的预制拼装桥墩。该桥为跨度40 m的混凝土简支箱梁桥，墩高10 m，截面尺寸为2.4 m×2.2 m，承台尺寸为5.8 m×5.8 m×2 m，墩身和承台均采用C40混凝土。桥墩主筋全截面配筋率为0.76%，体积配箍率为0.57%。该桥抗震设防烈度为8度，设计基本地震动加速度为0.2g，场地类别为Ⅲ类，设计分组为第一组。

选取单个桥墩为分析对象，并考虑上部梁体的惯性效应，将桥墩等分为四个节段，每个节段高2.5 m，构件尺寸和节段内配筋水平不变。在桥墩截面中心处设置预应力孔道，将1 860 MPa级无粘结预应力钢绞线分别锚固于盖梁和承台中，相邻节段间设置所提出的组合式剪力键，预制拼装桥墩的结构方案如图2所示。

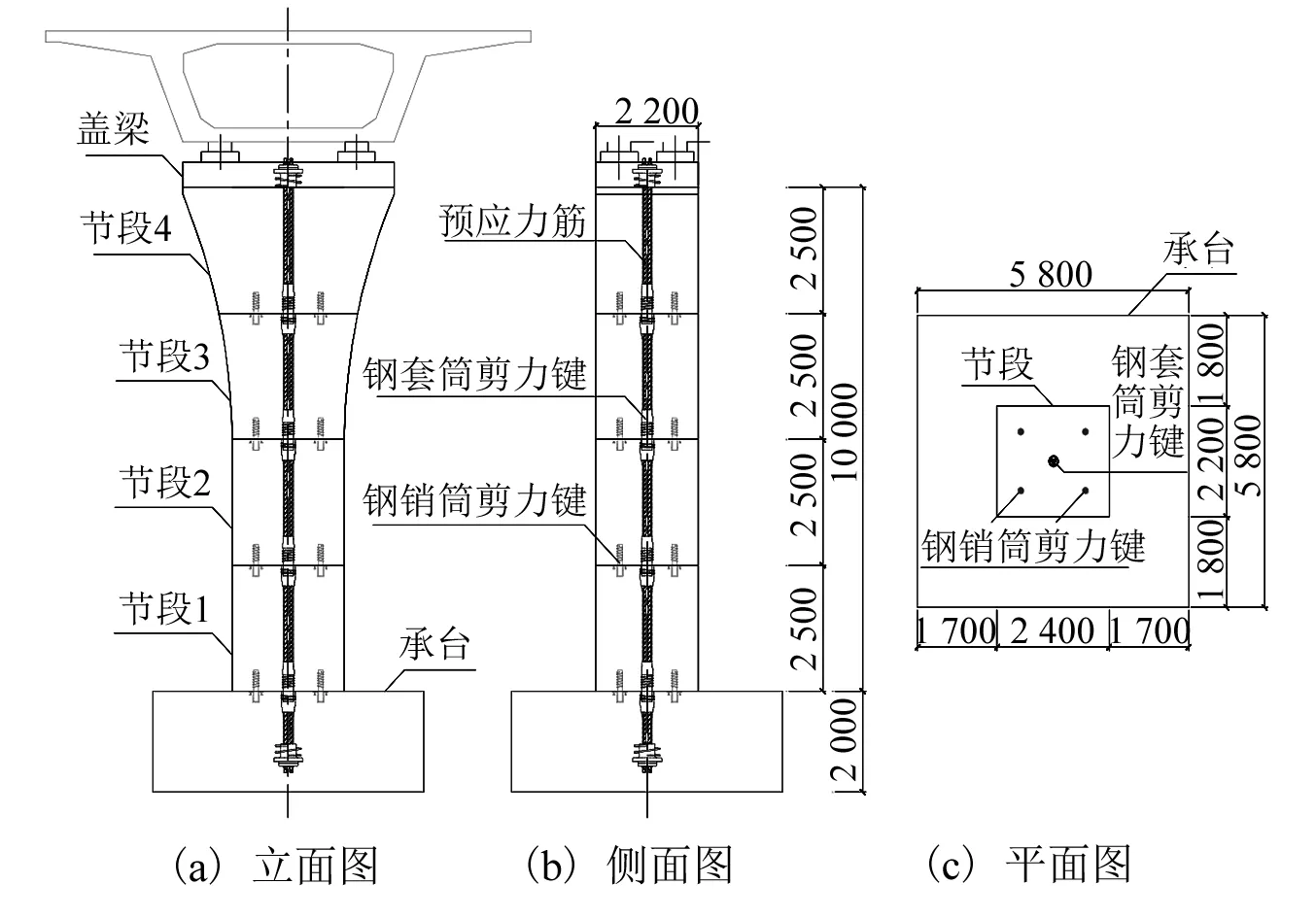
图2 预制拼装桥墩构造图(mm)Fig.2 Structural diagram of precast segmental pier (mm)

2 预制拼装桥墩数值模拟方法及验证

本节以既有拟静力试验结果为基准，验证基于ABAQUS平台的实体模型数值模拟方法的可靠性和准确性。

2.1 桥墩试件拟静力试验概况

高婧等[4]设计了三种预制拼装桥墩，通过拟静力试验比较分析了不同类型类桥墩的力学特性及损伤发展规律，本文以UBPC-S试件的结果进行对比验证。如图3所示，试件UBPC-S高1 600 mm，截面尺寸为240 mm×180 mm，承台尺寸为700 mm×700 mm ×420 mm，加载端尺寸为600 mm×600 mm×360 mm。混凝土设计强度为C40，纵筋采用10根Φ10的HRB335热轧钢筋，箍筋采用Φ6的R235光圆钢筋，节段1箍筋间距为50 mm，其余为80 mm。预应力筋采用2根Φ12.7的钢绞线，有效预加压力共130 kN，试件上部恒载为116 kN。

图3 试验桥墩尺寸及配筋图(mm)Fig.3 Dimension and reinforcement details of the test specimen (mm)

2.2 试验桥墩的精细化有限元建模

为准确描述强震下混凝土的材料非线性，采用三维实体减缩积分单元(C3D8R)模拟混凝土，其本构采用混凝土损伤塑性模型(concrete damaged plasticity,CDP)，该模型可用于模拟混凝土在单调、循环及动力荷载作用下的非线性行为。单轴受压应力-应变关系采用Mander非约束混凝土模型[15]，如式(1)所示；单轴受拉应力-应变关系采用断裂能开裂准则模型[16]，抗拉强度f′t采用式(2)计算

(1)

(2)

式中：σc为混凝土压应力；f′c0为非约束混凝土圆柱体抗压强度；x=εc/εc0为混凝土压应变与混凝土峰值应变的比值；r是与混凝土弹性模量相关的参数，具体含义详见文献[15]。

预应力筋采用C3D8R单元模拟，普通钢筋采用桁架单元(T3D2)模拟，两者均采用理想弹塑性模型，各类材料的参数取值见表2。

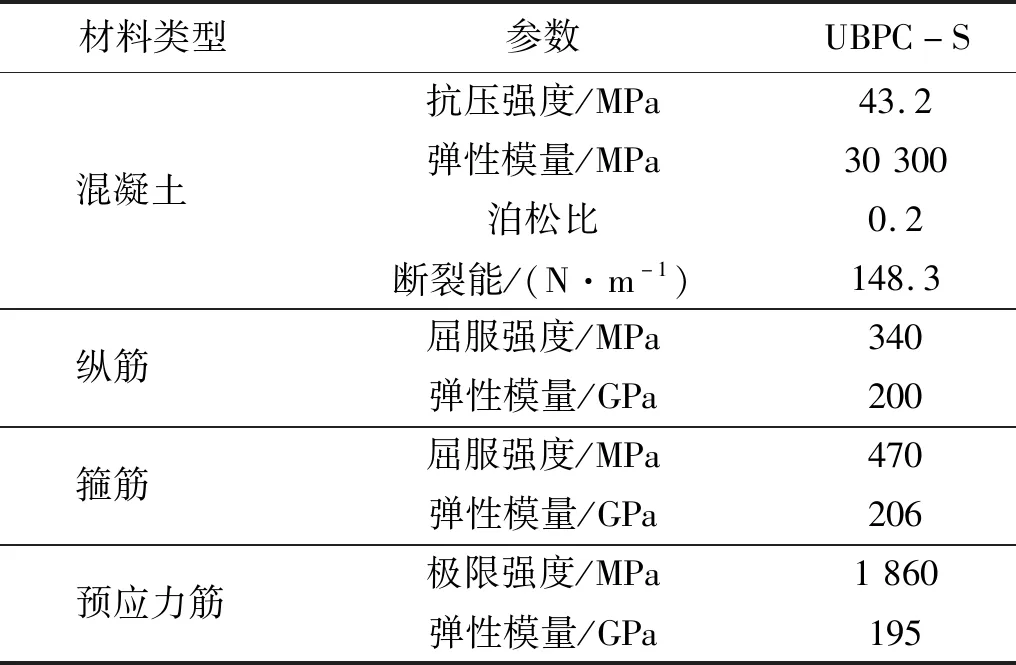
表2 材料参数Tab.2 Properties of the materials

为准确模拟预制拼装桥墩在侧向荷载作用下出现的接缝开合及节段滑移扭转现象，混凝土节段间、预应力筋与混凝土间采用“面-面接触对”，接触面法线和切线方向分别采用“硬接触”与“库仑摩擦模型”。混凝土节段间的摩擦因数为0.5，其余摩擦因数均为0。

试件承台底部约束所有自由度，上部恒载及侧向位移荷载通过耦合参考点施加于加载端顶面，荷载大小与试验保持一致。预应力筋锚固端和普通钢筋均“嵌入(embedded)”到混凝土中，预应力采用初始应力法施加。所建立的桥墩有限元模型如图4所示。

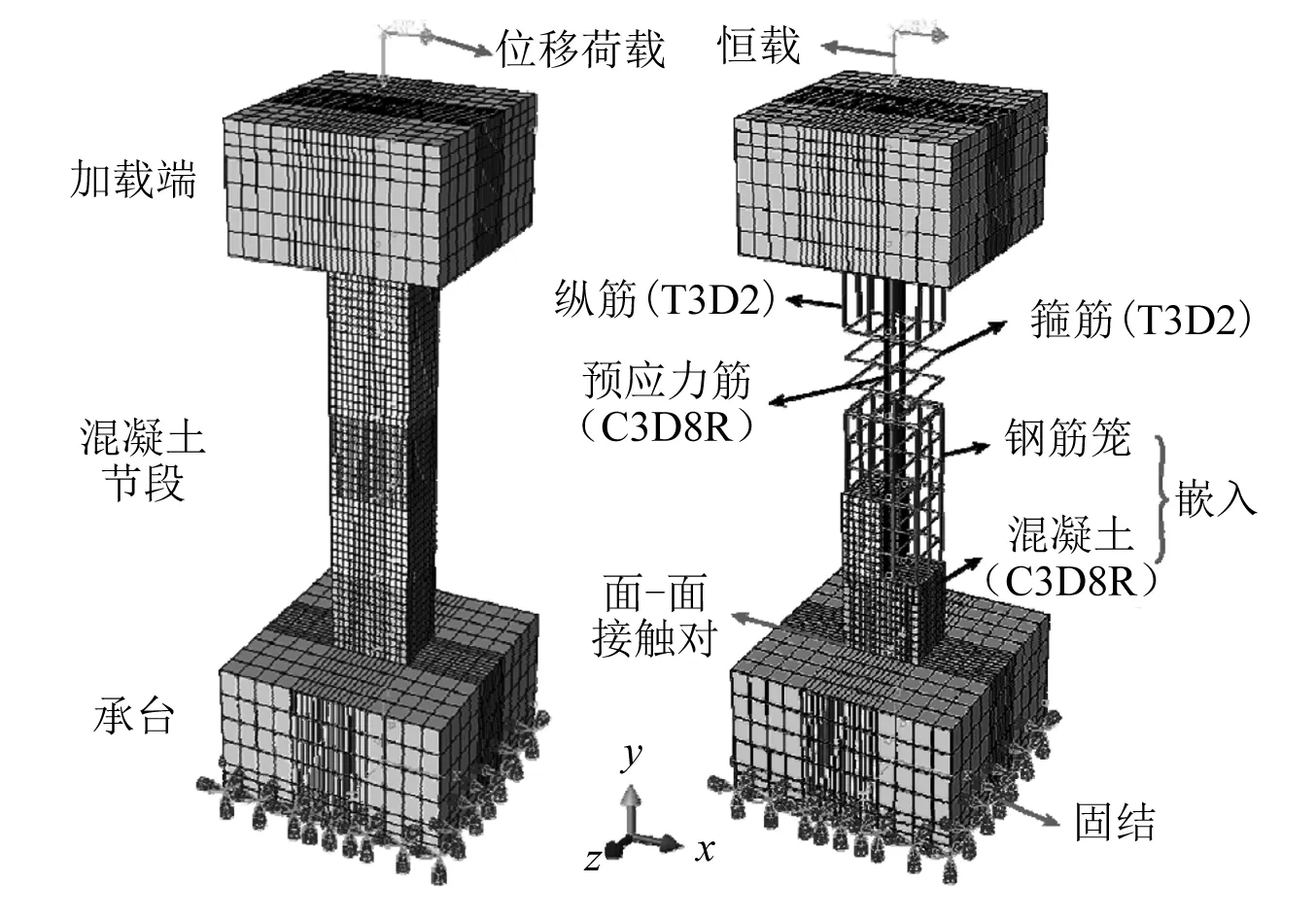
图4 试件桥墩有限元模型Fig.4 Finite element models of the specimen

2.3 模拟结果对比及验证

为验证上述数值模拟方法的可靠性，从墩底接缝变形和桥墩滞回曲线两个角度进行对比，如图5和图6所示。

图5(a)为试件墩底接缝开口对比，可看出，模拟结果与试验结果在接缝开口为正值时拟合较好，负值时匹配较差。这是因为CDP模型通过定义损伤系数来表征混凝土的损伤程度，虽然单元的塑性变形可一定程度上考虑接缝处的挤压行为，但仍难以模拟局部剥落现象，因此低估了接缝挤压变形，这也是数值模拟技术有待完善的方向之一。图5(b)给出了模拟试件墩底接缝滑移变形曲线。由试验实测结果可知，试件在试验过程中出现了滑移现象，最大滑移量达2 mm，模拟所得最大滑移量为0.83 mm，造成模拟误差较大的原因是试验过程中混凝土剥落导致接缝处混凝土接触面积减小产生滑移，而数值模拟难以模拟该现象，导致接缝处滑移变形比试验结果小。

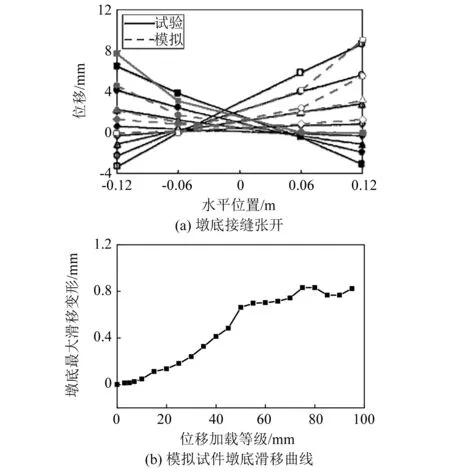
图5 试件墩底接缝变形对比Fig.5 Comparison of joint deformation at bottom of specimen

图6为拟静力试验与数值模拟所得滞回曲线的对比，可看出，两类曲线正向加载的总体形状和分布特征相一致，负向加载的匹配度相对较差，最大墩底剪力的模拟结果相对于试验测试值的误差仅为1.8%。总体来看，本文所采用的数值方法可较为准确地模拟预制拼装桥墩的力学行为，可用于后续研究。

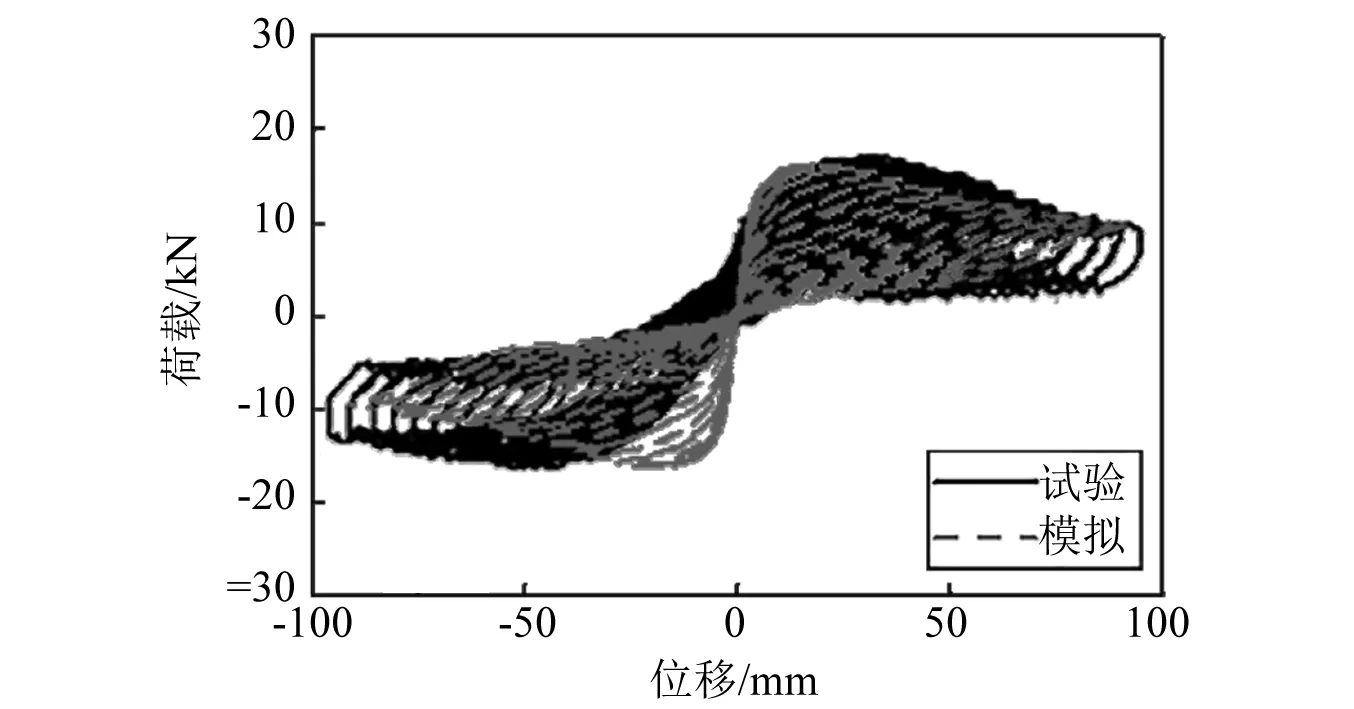
图6 模拟滞回曲线与试验滞回曲线对比Fig.6 Comparison between hysteresis curves by numerical simulation and model test

3 预制拼装桥墩抗震性能的影响因素分析

以1.2节提出的新型预制拼装桥墩结构为对象，采用2.2节所验证的模拟方法，并考虑组合式剪力键非线性接触行为，建立桥墩精细化有限元模型，通过拟静力分析揭示预应力筋配筋率、剪力键埋深、钢销棒直径对桥墩损伤破坏的影响规律与机理，具体工况设置见表3。

表3 预制拼装桥墩分析工况设置Tab.3 Working conditions of precast segmental pier

3.1 数值模型建立

组合式钢套筒(销棒)剪力键为Q345钢，采用C3D8R单元模拟，其材料本构采用双线性理想弹塑性模型，有限元模型如图7(b)～图7(c)所示。剪力键“嵌入”混凝土中，钢销棒及钢套管内管与外管间、预应力筋与钢套筒间均采用“面-面接触对”，不考虑界面摩擦力。位移循环荷载沿横桥向(图7中x轴)加载，位移大小依次为墩高的±0.5%、±1.0%、±1.5%、±2.0%、±3.0%、±4.0%、±5.0%、±6.0%、±7.0%，其余构件及边界条件的模拟方法同2.2节。组合式剪力键预制拼装桥墩的有限元模型如图7(a)所示。

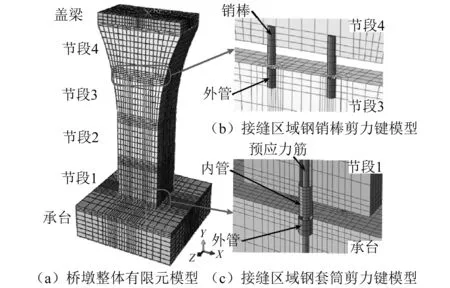
图7 预制拼装桥墩及组合式剪力键有限元模型Fig.7 Finite element models of the proposed precast segmental pier and combined shear keys

3.2 预应力筋配筋率的影响

根据文献[17]的研究成果，本文选取预应力筋的初始张拉应力为屈服强度的50%不变，讨论预应力筋配筋率对桥墩抗震性能的影响规律。按照JTG/TB 02-01—2008《公路桥梁抗震设计细则》对规则桥梁轴压比的规定，拟定预应力筋配筋率范围(prestressed tendon ratio,PR)为0.04%～0.76%，相应桥墩总轴压比ηk为0.05～0.3，见表3中的工况1～6。

图8分别给出了不同预应力筋配筋率下预制拼装桥墩的滞回曲线(图8(a))，以及墩顶残余位移随桥墩侧移量的分布(图8(b))。可看出，由于节段间干接缝、无粘结预应力筋及上部结构质量的共同作用，桥墩滞回曲线“捏缩”现象明显，呈现稳定的旗帜形。预应力筋配筋率对拼装桥墩的抗震性能影响显著，增大预应力筋配筋率可显著提高桥墩的抗剪能力，同时也会增加墩顶残余位移。当预应力筋配筋率由0.04%增加至0.76%，墩底最大剪力提高了4倍，墩顶最大残余位移由0.01 m增加至0.15 m。这是因为，增大轴压比可增强桥墩极限承载力，同时增加墩底混凝土塑性变形和墩顶残余位移。

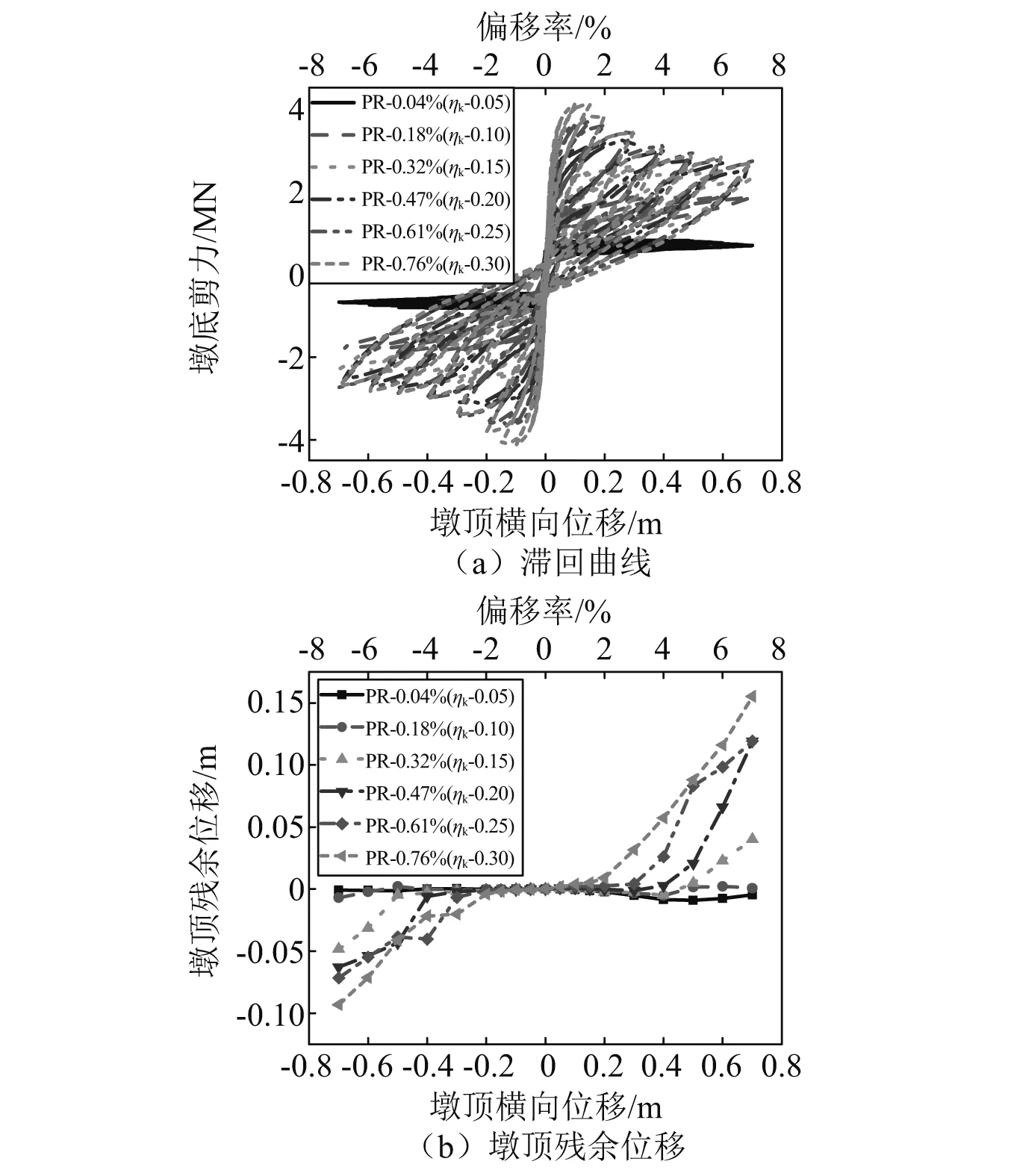
图8 预应力筋配筋率对桥墩抗震性能的影响Fig.8 Effect of prestressed tendon ratio on seismic performance of precast segmental piers

图9给出了不同配筋率水平下预应力筋的应力分布曲线，图10给出了不同预应力筋配筋率的桥墩在偏移率为5%时，节段1混凝土受压损伤因子的分布云图。可发现，随预应力筋配筋率的增加，其最大应力和残余应力均逐渐减小，预应力损失(有效应力与残余应力的差值)呈先减小后增大的趋势，混凝土损伤逐渐加重。这是因为，预应力筋配筋率为0.04%时，预应力筋在桥墩偏移率为5%时发生屈服(最大应力为1 807 MPa)，相邻两循环路径间距增大(图9(a))，预应力损失率达54.37%，但混凝土基本完好(图10(a))。配筋率为0.76%时，墩底外侧混凝土损伤严重(图10(c))，预应力筋的应力变化曲线呈现较饱满的抛物线形(图9(c))，预应力损失率为40.79%。本文计算结果表明，通过合理调整预应力筋配筋率，使桥墩总轴压比为0.15时，预应力损失率可控制在5%以内，混凝土不会出现严重损伤(如图9(b)和图10(b)所示)，可同时最大程度地发挥预应力筋和混凝土的性能。

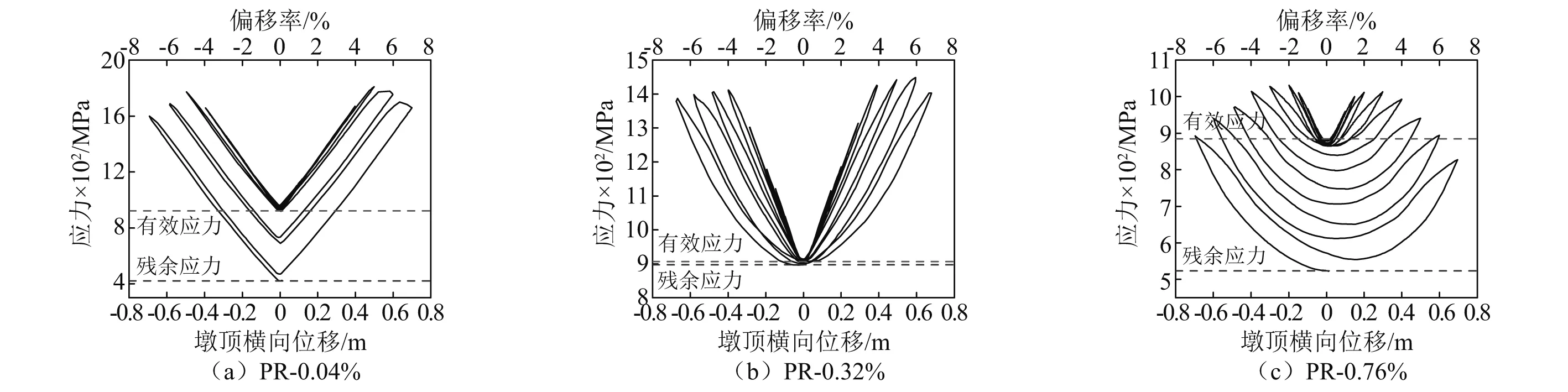
图9 不同配筋率下预应力筋应力对比Fig.9 Comparison of prestressed tendon stress under different prestressed tendon ratios

图10 偏移率为5%时节段1混凝土受压损伤因子分布云图Fig.10 Distribution cloud of concrete compression damage of No.1 segment at 5% drift

3.3 组合式剪力键的影响

为研究组合式钢套筒(销棒)剪力键对预制拼装桥墩抗震性能的影响，本文另建立了整体现浇桥墩(cast-in-place,CIP)、无剪力键的普通干接缝预制拼装桥墩(Dry Joint,DJ)模型，见图11和图12。开展了上述结构及组合式剪力键预制拼装桥墩(combined shear key,CSK)抗震性能的对比分析，各类桥墩的恒载轴压比相同，组合式剪力键桥墩的钢销棒直径为120 mm，剪力键埋深为300 mm。图13给出了不同类型桥墩的滞回曲线、骨架曲线，可看出，通过调整预应力筋配筋率，预制拼装桥墩可达到与现浇整体墩相当的水平承载力，并具有良好的自复位能力。由图13(b)可知，组合式剪力键可有效提高预制拼装桥墩的抗剪承载力。当总轴压比为0.125和0.15时，组合式剪力键预制拼装桥墩的抗剪承载力分别为2 316.04 kN和2 686.46 kN，相较于无剪力键时分别提高了6.62%和3.26%。随着预应力筋配筋率的增加，剪力键对桥墩承载力的提升作用逐渐减弱，设计时应特别注意预应力筋与剪力键对桥墩极限承载力的贡献大小。

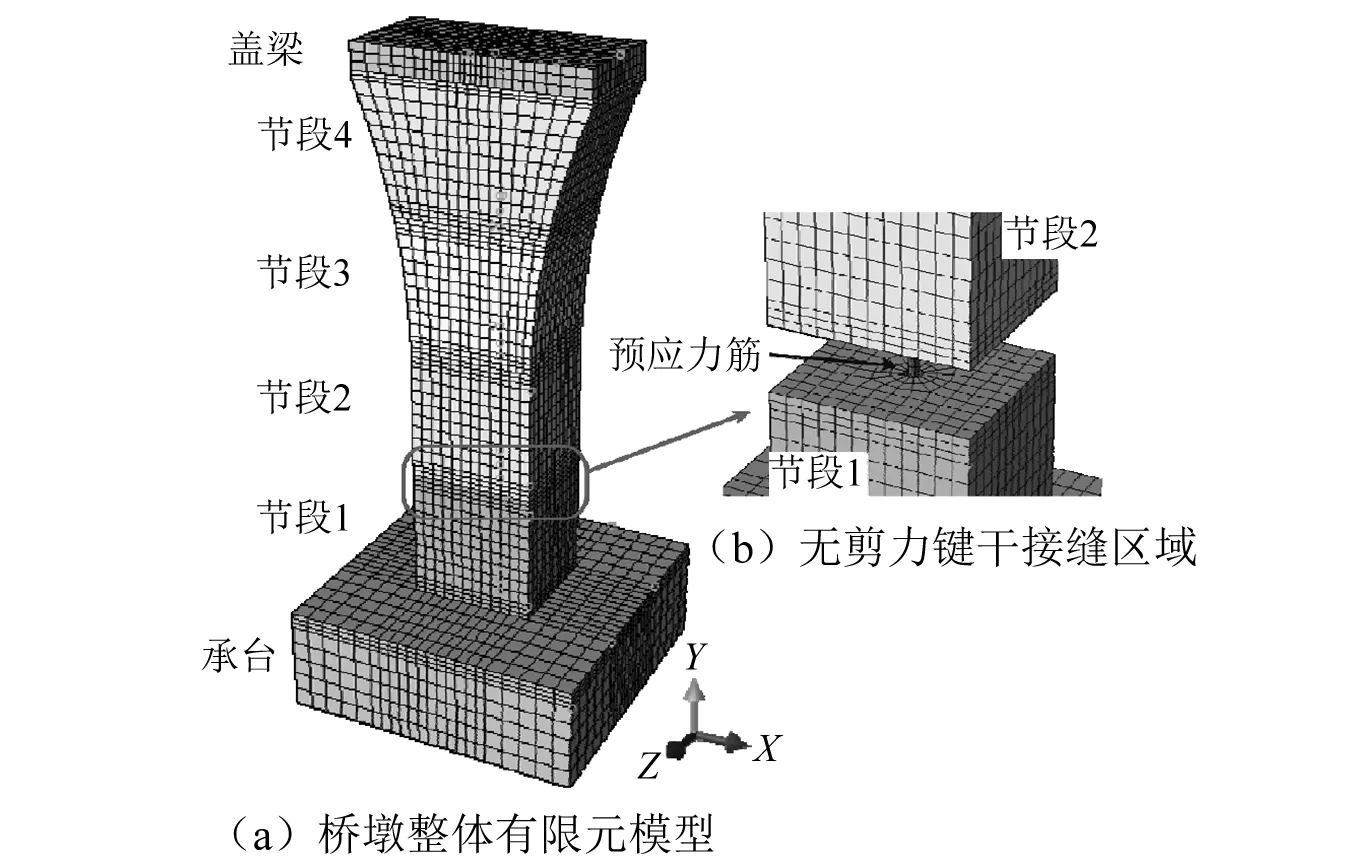
图11 无剪力键预制拼装桥墩有限元模型Fig.11 Finite element model of precast segmental bridge pier without shear keys

图12 整体现浇墩纤维模型Fig.12 Finite element model of cast-in-place bridge pier

图13 组合式剪力键对桥墩抗震性能的影响Fig.13 Effect of combined shear key on seismic performance of bridge piers

3.4 剪力键埋深的影响

拟定预应力筋配筋率为0.18%，钢销棒直径为120 mm，讨论剪力键埋深H对桥墩抗震性能的影响，分别调整剪力键埋深为混凝土保护层厚度的1倍、2倍、3倍和4倍(即100 mm，200 mm，300 mm和400 mm)，见表3中所列工况2和工况7-9。图14给出了无剪力键墩及其他不同剪力键埋深桥墩的滞回曲线、骨架曲线。可看出，设置组合式剪力键预制拼装桥墩的抗剪能力均强于无剪力键墩。当剪力键埋深为100 mm且偏移率达到7%时，滞回曲线严重不对称，墩底剪力突降至极限承载力的63.8%，桥墩出现脆性破坏。随着剪力键埋深的增加，桥墩抗剪能力有所提高，埋深为300 mm和400 mm时，骨架曲线基本重合，说明埋深达到一定程度时，桥墩极限承载力趋于稳定。

图14 剪力键埋深对预制拼装桥墩抗震性能的影响Fig.14 Effect of embedded depth of shear key on seismic performance of precast segmental piers

为揭示剪力键浅埋深时桥墩出现脆性破坏的原因，图15给出了埋深为100 mm和400 mm时，与7%偏移率相对应的墩底局部应力云图的对比。可看出，剪力键埋深为100 mm时，墩底接缝张开达154.8 mm，受拉侧剪力键完全拔出，由其承担的剪力突然转移，导致接缝处预应力筋严重颈缩，如图15(a)所示，预应力筋最大应力达到极限应力(1 860 MPa)，完全丧失功能，宏观表现即为桥墩的脆性破坏，因此应控制剪力键的最小埋深。

图15 偏移率为7%时墩底局部应力云图Fig.15 Stress cloud of pier bottom at 7% drift

3.5 剪力键钢销棒直径的影响

拟定预应力筋配筋率为0.18%、剪力键埋深为300 mm，讨论钢销棒直径D对桥墩抗震性能的影响。将钢销棒与桥墩截面剪切刚度之比作为设计剪力键直径的参考指标，分别选取刚度比为0.01，0.03，0.05和0.10进行研究，对应的钢销棒直径分别为55 mm，95 mm，120 mm和170 mm，见表3中所列工况2和工况10～工况12。图16给出了无剪力键墩及其他不同钢销棒直径桥墩的滞回曲线、骨架曲线，可看出，桥墩屈服前骨架曲线基本重合，初始刚度依次为155.83 MN·m-1，162.07 MN·m-1，163.31 MN·m-1，163.82 MN·m-1和164.48 MN·m-1。这是因为，实际工程中剪力键钢销棒与钢管之间由于构造需要和施工误差势必存在初始间隙，本文通过设置1 mm间隙量予以考虑，因此当墩顶横向位移很小时，钢销棒与钢管之间尚未接触，暂不参与提供剪切刚度，故而增大钢销棒直径对桥墩初始刚度无明显影响。组合式剪力键预制拼装桥墩的抗剪能力均强于无剪力键墩，随着墩顶侧移量逐渐增大，先后出现节段间接缝张开、错动以至剪力键拔出，导致钢销棒侧壁与外管紧密接触，从而增强桥墩的抗剪能力。对于钢销棒直径170 mm工况，当桥墩偏移率为7%时，墩顶出现比较明显的残余位移(约0.03 m)，因此钢销棒直径的选取不是越大越好，需在保证承载能力的同时兼顾墩顶残余位移的限制。

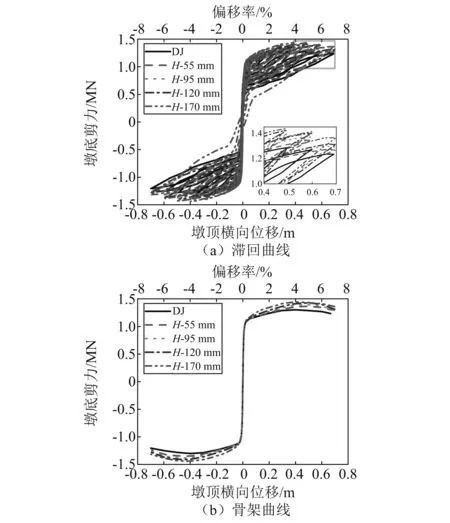
图16 钢销棒直径对预制拼装桥墩抗震性能的影响Fig.16 Effect of diameter of steel dowel on seismic performance of precast segmental piers

4 不同类型地震动下的动力响应对比检验

为进一步检验所提出的预制拼装桥墩方案的合理性，本节选取近远场地震动开展非线性时程分析，对比讨论组合式剪力键对桥墩动力响应的影响规律。

4.1 地震动选取

按照以下原则选取地震动：①桥梁所处场地类别为Ⅲ类，设计分组为第一组，考虑中外规范中场地类别划分标准的差异，平均剪切波速V30的范围为150～260 m·s-1[18]；②强震记录的震级大于6.0级；③远场地震动的断层距大于30 km，近场地震动的断层距小于20 km；④脉冲型地震动应具有明显的速度脉冲，且脉冲持时大于1 s；⑤参考双频段法[19]，所选地震动的加速度谱在结构基本自振周期(0.624 s)和平台段处与规范设计谱的均方差小于10%。

所选地震动记录均包含两个垂直方向的加速度时程，定义峰值较大的加速度时程为主地震动，另一方向为次地震动，各组地震动的主要参数如表4所示。地震动水平双向输入，主地震动作用于横桥向(图7及图11中x轴)，其加速度峰值调幅为0.4g(罕遇地震水平)，次地震动作用于顺桥向(z轴)，按主地震动比例调幅。

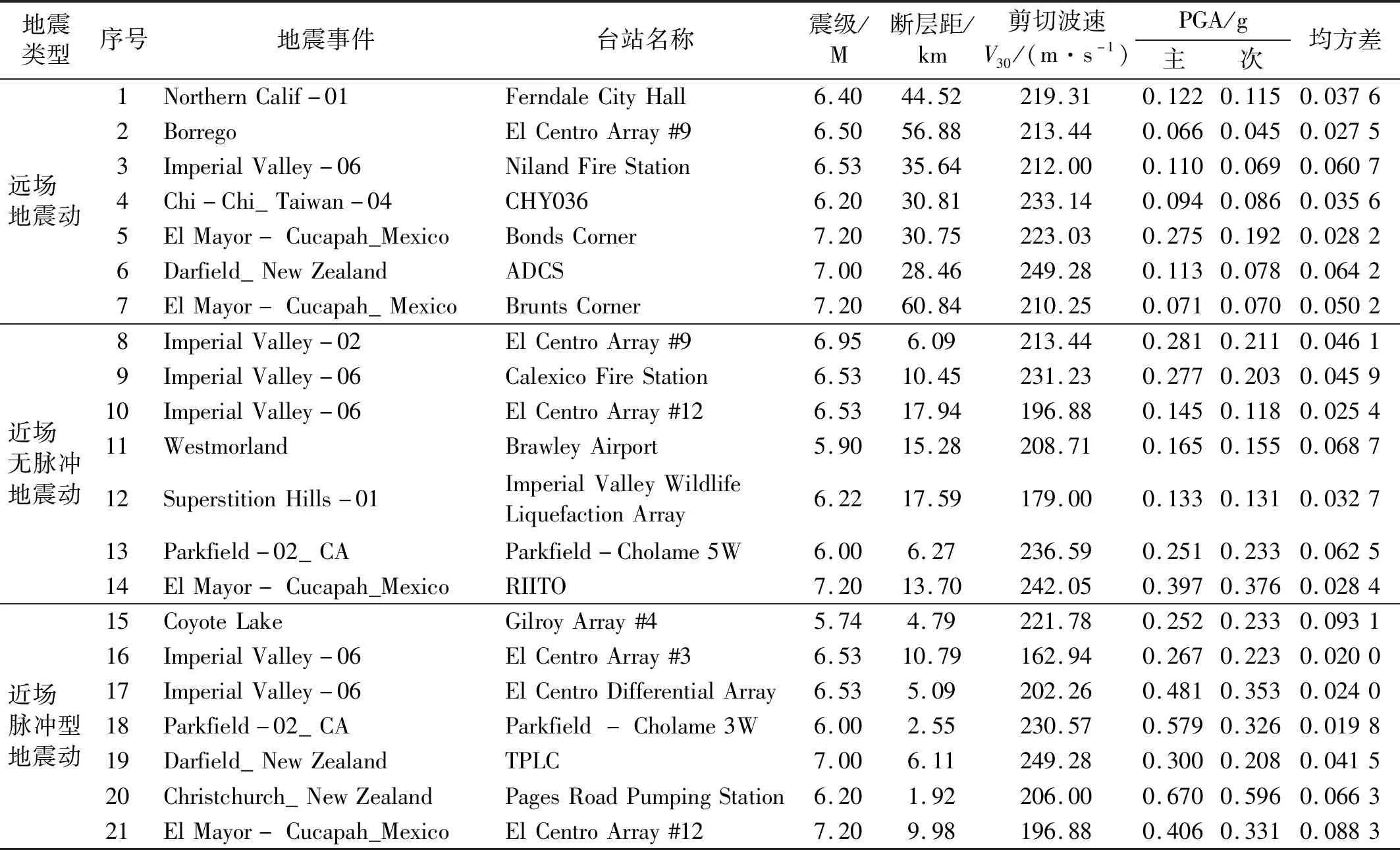
表4 所选取的地震记录Tab.4 Earthquake records selected

4.2 地震响应对比分析

为研究组合式剪力键在实际地震作用下对预制拼装桥墩抗剪扭能力的提升效果，本节分别计算参数优化后的预制拼装桥墩(PT-0.32%，H-300 mm，D-120 mm)和无剪力键桥墩的动力响应。

表5列出了有无剪力键的预制拼装桥墩动力响应峰值的均值。对比可看出，组合式剪力键可显著降低桥墩位移响应，并提高桥墩抗剪扭能力。以横桥向响应为例，有剪力键桥墩相较于无剪力键桥墩在远场、近场无脉冲及近场脉冲型地震动作用下的墩顶最大位移分别降低29.30%、27.46%、9.97%，墩底剪力分别提高了0.99%、1.64%、0.76%。

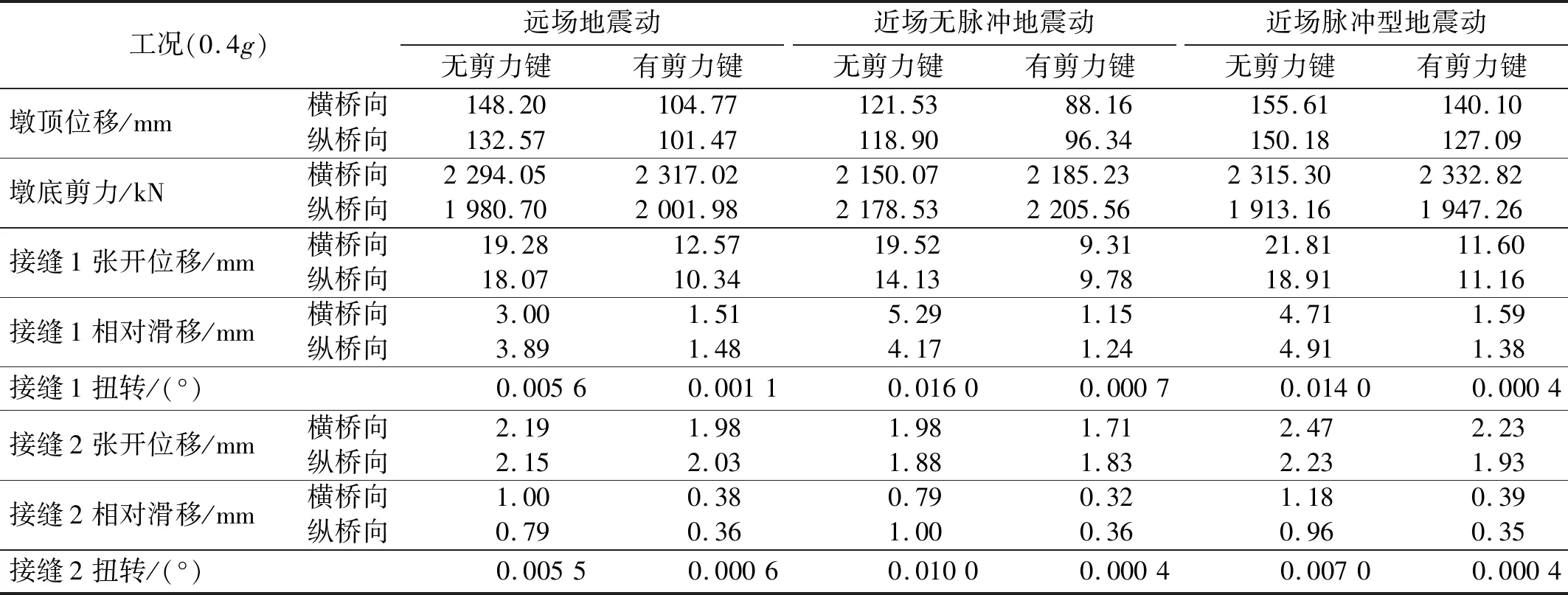
表5 有无剪力键桥墩的动力响应Tab.5 Dynamic response of the pier with or without shear keys

由接缝处局部变形可看出，设置组合式剪力键可有效限制接缝张开及节段间滑移扭转。限于篇幅，图17给出了17号地震动作用下桥墩接缝变形的时程曲线，可看出，设置剪力键使桥墩接缝1横桥向的张开、滑移及扭转变形分别降低51.58%、48.91%、95.24%。这是因为，桥墩受地震作用摇摆变形时，组合式剪力键随节段提离拔出，此时剪力键侧壁与预埋外管挤压接触，接缝张开受限。同时，钢销棒及钢套筒剪力键可共同发挥限位作用，防止节段出现侧向滑移和扭转。

图17 17号地震动作用下桥墩接缝变形时程曲线Fig.17 Time history curve of joint deformation under No.17 earthquake record

此外，不同类型地震动作用下桥墩的动力响应略有差别，对比两类近场地震动响应，速度脉冲对结构位移响应(墩顶位移、接缝张开位移)的影响更为明显，这和文献[20]的相关研究成果相一致。

5 结 论

(1)本文提出的组合式钢套筒(销棒)剪力键，具有构造简洁、稳定可靠、抗剪扭强度高等优点，可供预制拼装桥墩参考使用。

(2)与模型试验结果对比表明，所采用的装配式桥墩实体模型数值方法可准确描述局部接缝张开及滑移变形，可用于预制拼装结构的精细化数值模拟。

(3)增大预应力筋配筋率可显著提高桥墩的抗剪能力，但墩顶残余位移也随之增大。通过合理设置预应力筋配筋率，可使预制拼装桥墩具有与现浇桥墩相当的承载力，并可同时充分发挥预应力筋和混凝土的性能，避免某一材料过早破坏。

(4)增加剪力键埋深和钢销棒直径均可一定程度上提高桥墩的承载力，桥墩抗震性能随剪力键埋深的进一步增大趋于稳定，墩顶残余位移随钢销棒直径的提高逐渐增大，应合理控制剪力键最小埋深和钢销棒最大直径。

(5)双向水平地震作用下，组合式剪力键可有效限制接缝张开及滑移扭转变形，提高桥墩的抗剪扭能力。不同类型地震动对预制拼装桥墩的动力响应略有影响，速度脉冲对桥墩位移响应的放大作用较为明显。

需说明的是，本文主要采用数值方法分析、检验了所提出组合式拼装桥墩结构方案的可行性，还有必要通过动静力模型试验进行深化研究。