钢筋混凝土受弯构件配筋率影响因素及变化规律研究①

曹 锋

(青海民族大学建筑工程学院,青海 西宁 810000)

0 引 言

现行《混凝土结构设计规范》GB50010-2010对混凝土结构受弯构件的配筋率允许范围是比较大的，单筋矩形梁的经济配筋率在0.6%—1.5%之间[1]，配筋率对构件的安全性能、经济性能及耐久性能有重要的影响，配筋率很大程度上影响钢筋混凝土受弯构件的可靠性[2～3]。构件截面尺寸的变化、钢筋及混凝土强度等级的变化以及所受外力大小的变化，都将引起钢筋混凝土受弯构件配筋率的改变。钢筋混凝土受弯构件纵向配筋率大，构件的受力性能较好，但过高会造成构件的脆性破坏。同时造成钢筋绑扎与混凝土浇筑困难，施工质量难以保证[4]。当钢筋混凝土受弯构件需要承受较大内力时，增大截面尺寸与提高配筋率，对工程质量、耐久性与工程造价均会产生一定影响[5～6]。因此，研究钢筋混凝土受弯构件配筋率的影响因素，以及随着各因素的变化规律，对钢筋混凝土受弯构件的设计、施工具有重要的指导意义。

1 正截面受弯承载力计算原理与方法

1.1 基本假定

《混凝土结构设计规范》规定，包括受弯构件在内的各种混凝土构件的正截面承载力应按下列五个基本假定进行计算：

(1)截面应保持平面；

(2)不考虑混凝土的抗拉强度；

(3)混凝土受压的应力与应变关系曲线按下列规定取用：

当εcε0时(上升段)

(1)

当ε0<εcεcu时(水平段)

σc=fc

(2)

式中，参数n、ε0和εcu的取值如下，fcu,k为混凝土立方体抗压强度标准值。

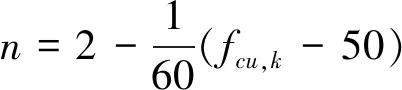
(3)

ε0=0.002+0.5×(fcu,k-50)×10-5≥0.002

(4)

εcu=0.0033-(fcu,k-50)×10-50.0033

(5)

(4)纵向受拉钢筋的极限拉应变取为0.01；

(5)纵向钢筋的应力取钢筋应变与其弹性模量的乘积，但其值应符合下列要求：

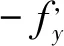
(6)

式中，σsi为第i层纵向普通钢筋的应力，正值代表拉应力，负值代表压应力。

1.2 基本计算公式

单筋矩形截面受弯构件正截面受弯承载力计算简图如图1所示，图中的x称为混凝土受压区高度，z称为内力臂[7]。

由力的平衡条件，得

α1fcbx=fyAS

(7)

由力矩平衡条件，得

(8)

或

(9)

适用条件：

ρs或xξbh0，或ξξb，为了防止超筋破坏；

(10)

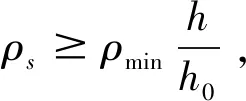
(11)

其中：ρs称为钢筋混凝土受弯构件的配筋率；ρb称为界限配筋率；ρmin称为最小配筋率。

1.3 正截面受弯承载力与配筋率计算方法

2 配筋率影响因素及变化规律

由前述内容可知，配筋率的影响因素主要有截面的高度、宽度以及配筋面积，而根据平衡方程，配筋面积和混凝土、钢筋的强度等级以及受力大小有关。因此，截面高度、宽度变化，混凝土、钢筋的强度等级变化，构件的受力大小变化，都会影响配筋率的变化。对如下工程实例进行研究，钢筋混凝土矩形梁，截面尺寸为b×h=250mm×750mm，环境类别为一类，弯矩设计值M=180kN·m，混凝土强度等级为C30，钢筋采用HRB400级钢筋。分别改变其梁截面尺寸、材料强度等级及构件受力，确定配筋率的影响因素及其变化规律。

2.1 截面尺寸影响

根据规范要求，矩形截面梁的高宽比一般取为2.0～3.5之间。截面宽度及高度的变化，均会引起配筋率发生变化。

2.1.1 截面高度变化影响

对上述计算实例，同样的混凝土强度等级C30、钢筋强度等级HRB400、截面宽度250mm及相同内力180kN·m作用下，分别采用截面高度为400mm、450mm、500mm、550mm、600mm、650mm、700mm、750mm，按上述方法求得其理论配筋率，统计于表1。

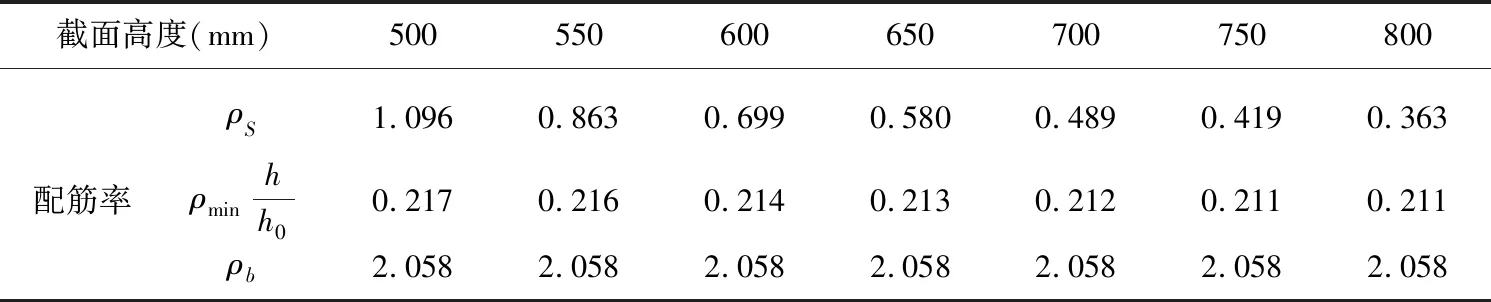
表1 不同截面高度计算得到的配筋率(%)

将表1的计算结果绘制于图2 ，可得钢筋混凝土受弯构件配筋率随着梁截面高度的变化关系曲线。

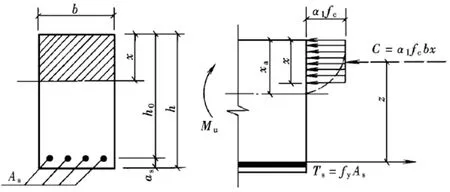
图1 单筋矩形截面受弯构件正截面受弯承载力计算简图

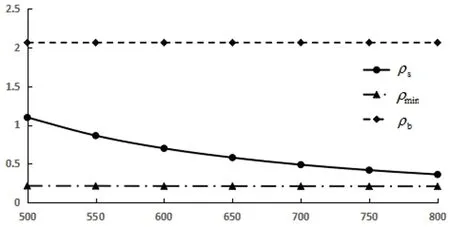
图2 配筋率随截面高度变化关系

由图2得知，随着构件截面高度的增加，配筋率呈减小趋势，对最小配筋率影响较小，对界限配筋率没有影响，而梁截面高度变化对钢筋混凝土受弯构件配筋率影响较大。

2.1.2 截面宽度变化影响

对上述计算实例，同样的混凝土强度等级C30、钢筋强度等级HRB400、截面高度750mm及相同内力180kN·m作用下，分别采用截面宽度为200mm、250mm、300mm、350mm，按上述方法求得其理论配筋率，统计于表2。并将表2的计算结果绘制于图3 ，可得钢筋混凝土受弯构件配筋率随着梁截面宽度的变化关系曲线。

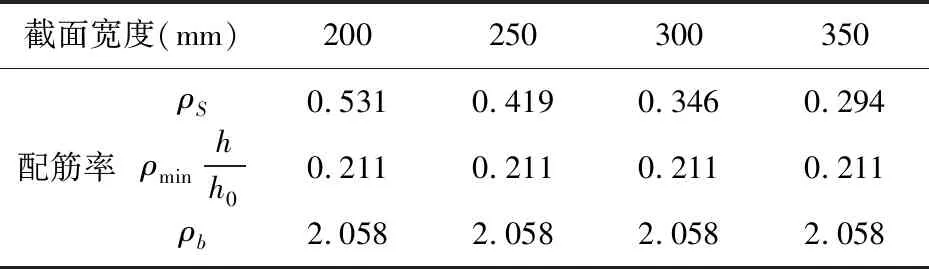
表2 不同截面宽度计算得到的配筋率(%)

由图3得知，随着构件截面宽度的增加，配筋率呈减小趋势，对最小配筋率及界限配筋率均没有影响，梁截面宽度变化对钢筋混凝土受弯构件配筋率影响较大。

2.2 材料强度影响

在截面尺寸及受力不变的情况下，改变混凝土及钢筋的材料强度等级，分析其对配筋率的影响及其变化规律。

2.2.1 混凝土强度等级影响

对上述计算实例，同样的截面尺寸250mm×750mm、钢筋强度等级HRB400及相同内力180kN·m作用下，分别采用混凝土强度等级为C30、C35、C40、C45、C50、C60、C80，计算理论配筋率，统计于表3。

表3 不同混凝土强度下计算得到的配筋率(%)

将表3的计算结果绘制于图4 ，可得钢筋混凝土受弯构件配筋率随着梁混凝土强度的变化关系曲线。

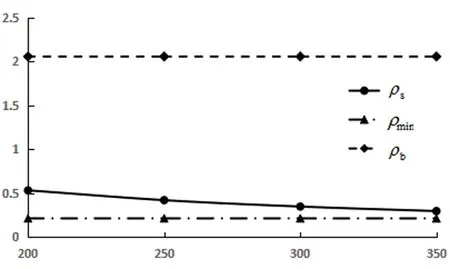
图3 配筋率随截面宽度变化关系

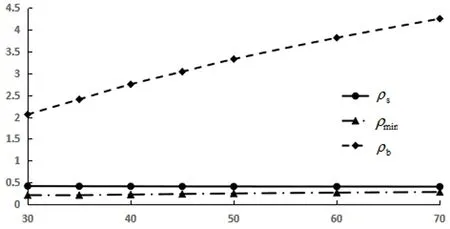
图4 配筋率随混凝土强度等级变化关系

由图4得知，随着混凝土强度等级的提高，配筋率呈减小趋势，但变化幅度微小。最小配筋率及界限配筋率，均随混凝土强度等级的提高而增大，最小配筋率的变化较小，而界限配筋率的变化较为显著。

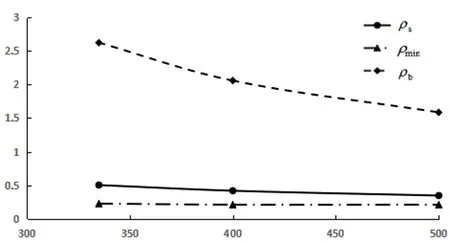
图5 配筋率随钢筋强度等级变化关系

图6 配筋率随弯矩变化关系

2.2.2 钢筋强度等级影响

对上述计算实例，同样的截面尺寸250mm×750mm、混凝土强度等级为C30及相同内力180kN·m作用下，分别采用钢筋强度等级为HRB335、HRB400、HRB500，计算理论配筋率，统计于表4,并将表4的计算结果绘制于图5 ，可得钢筋混凝土受弯构件配筋率随钢筋强度等级的变化关系曲线。

表4不同钢筋强度等级下计算得到的配筋率(%)

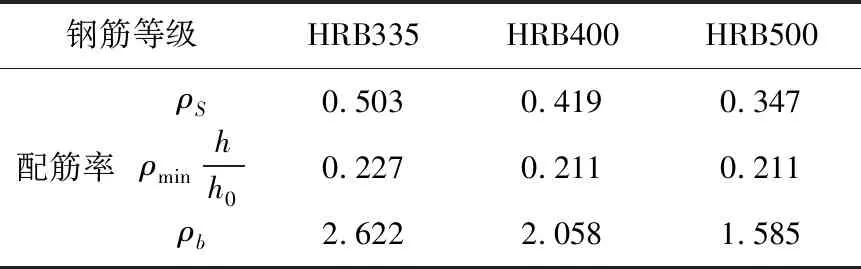
钢筋等级HRB335HRB400HRB500ρS0.5030.4190.347配筋率ρminhh00.2270.2110.211ρb2.6222.0581.585

由图5得知，随着钢筋强度等级的提高，配筋率呈减小趋势，变化幅度较小。最小配筋率及界限配筋率，均呈减小趋势，最小配筋率的变化较小，而界限配筋率的变化较为显著。

2.3 构件受力影响

在截面尺寸及材料强度等级不变的情况下，改变钢筋混凝土受弯构件所受到弯矩大小，分析其对配筋率的影响及其变化规律。

对上述计算实例，同样的截面尺寸250mm×750mm、混凝土强度等级为C30及钢筋强度等级为HRB400作用下，分别采用弯矩大小为100kN·m、150kN·m、180kN·m、200kN·m、250kN·m、300kN·m，计算理论配筋率，统计于表5。

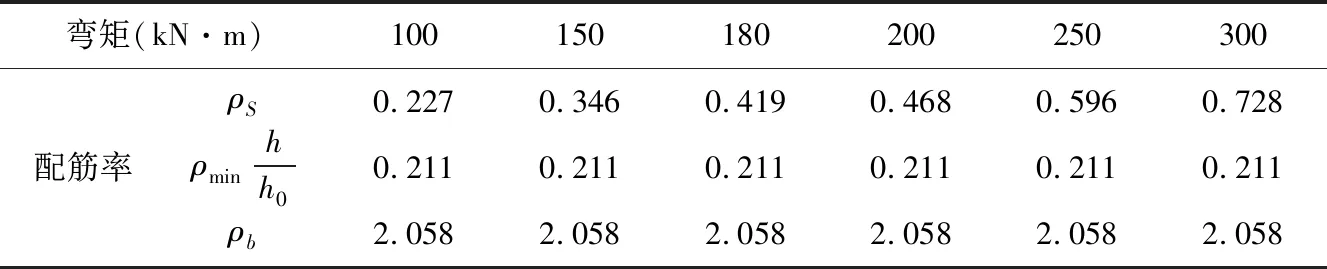
表5 不同弯矩作用下计算得到的配筋率(%)

将表5的计算结果绘制于图6 ，可得钢筋混凝土受弯构件配筋率随构件所受弯矩大小的变化关系曲线。

由图6得知，随着构件上作用的弯矩增大，配筋率呈增大趋势，变化幅度较大,最小配筋率及界限配筋率，均不发生变化，弯矩变化对其没有影响。

3 结 论

(1)钢筋混凝土受弯构件纵筋配筋率随构件截面尺寸发生变化。构件截面高度或宽度的增加，配筋率均呈减小趋势，且变化较为显著，而界限配筋率不发生变化。随截面高度增加，最小配筋率略微减小，而宽度变化对其没有影响。

(2)钢筋混凝土受弯构件纵筋配筋率随材料强度等级发生变化。混凝土及钢筋的强度等级提高，配筋率均呈减小趋势，且钢筋强度等级变化对配筋率的影响较为显著。混凝土强度等级提高，最小配筋率及界限配筋率均增大，且界限配筋率增大的更快。钢筋强度等级提高，最小配筋率及界限配筋率均减小，且界限配筋率减小的更快。

(3)钢筋混凝土受弯构件纵筋配筋率随构件上作用弯矩发生变化。构件上作用弯矩增大，配筋率呈增大趋势，变化较为显著。最小配筋率及界限配筋率，均不发生变化，弯矩变化对其没有影响。