典型截面超高层建筑横风向气动性能研究①
李 勇
(郑州工业应用技术学院建筑工程系,河南 郑州 450000)
0 引 言
随着社会的科技发展和城市人口的与日俱增,人们对于城市的容积量有了更高的要求,发达国家甚至提出了“空中城市”的概念。若想落实这一理念,必须要加大对结构高度和高强材料的分析,从多个角度研究超高层建筑在空中的受力情况,从而设计出有效的控制荷载,确保结构安全和居住的舒适性[1,2]。
在受力方面,超高层建筑与普通建筑有很大的不同,研究它的横风向气动性能对于建设抗风性建筑有关键性意义,国内外的风工程学家也致力于此方面的研究,不断提出新的思路和想法,在理论和实践的基础上做了大量风洞试验。超高层建筑横向风向的气动性能十分复杂,依靠多种机理形成,与顺风向气动性能有很大的不同,横风向气动性能不能依靠常规理论分析流速,只能通过实验分析,因此气动性能分析是建设高层建筑的基础工作[3]。
目前依旧没有成熟的方法分析截面超高层建筑横向风向气动性能[4]。在上述背景下研究典型截面超高层建筑横向风向气动性能,该研究对于以后建筑超高层建筑有一定的帮助。
1 典型截面超高层建筑横风向气动力的确定
确定典型截面超高层建筑横风向气动力可以通过气动弹性响应反演、刚性模型表面风压积分测量和高频动态天平测力三个步骤进行研究[5]。
如图1所示,确定典型截面超高层建筑横风向气动力是通过输入、处理和输出三步完成的,启动弹性响应反演可以检测出超高层建筑典型截面各种受力数据,通过刚性模拟表面风压积分测量处理得到的数据,最后使用高频动态天平测出风力和气流,作为输出结果显示出来[6]。
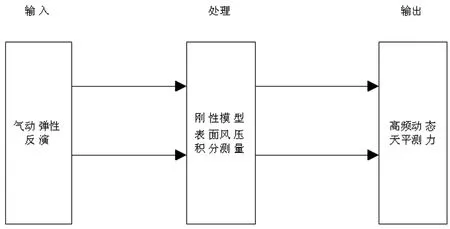
图1 典型截面超高层建筑横风向气动力的确定
1.1 气动弹性响应反演
使用单自由度气动弹性模型测试横风向位移,分析超高层建筑的动力特性参数,气动弹性响应反演法可以不考虑超高层建筑的气动反馈作用。
高层建筑由于形状不同所以受到的气流也不同,圆形、方形、凹角形的截面会根据高度不同受到不同的气动弹性。设定高层建筑物的基础状态与高度成正比,使用弹力支撑刚性模型,是模型维持在自由度状态下。应变平衡系统的顶部在受到横风向气流和顺风向气流时会产生不同的位移响应谱,在动力参数的影响下扩展成风向气动力谱,根据气动力谱可以研究顶部受到的风力[7]。高空中的横风向气动力可以分解成两种:外加气动力、气动阻尼力,随着风速的不同气动阻尼力的振幅不同,从而带来超高层建筑结构的共振[8]。超高层建筑受到的横向气流和顺向气流如下图2所示:
图2中f1、f2、f3、f4分别代表四栋不同的建筑物,x轴代表的是横向气流,y轴代表的是顺向气流,Q1、Q2、Q3、Q4分别表示不同建筑物受到的风力。观察图2可知,当建筑物与顺向气流维持的位置一致时,Q1和Q4对气流产生主要影响,当建筑物与横向气流维持的位置一致时,Q2和Q3对气流产生主要影响[9]。气动力谱分析法多是针对统一风速下的刚度建筑,对于不统一风速下的超高层建筑来说,该方法产生的误差比较大,取得的结果精度不足[10]。
1.2 刚性模型表面风压积分测量
在得到气动弹性后,对刚性模型表面风压进行分析,使用外加气动力和气动阻尼力计算估计出结构风荷载以及风力振动情况。刚性模型表面的气动阻尼力大小与建筑物的结构形状、运动幅度、所受风力和风场特性等多种因素有关[11]。一般而言,超高层建筑都是盾体结构,对雷诺数的感应能力很差,气动力谱既受结构外形影响,又受风场环境影响,通过对空间的划分了解建筑物在每个角度受到的风力[12]。
超高层建筑表面受到的风力与风压无关,但是由于理论和实际值存在假定带,所以很容易产生误差。若想减少这一误差,应尽可能多地加大测点数。在测量典型截面超高层建筑时很容易遇到测压管道幅度和相位失真以及测压通道有限这两个问题[13]。解决方案如下表1所示:

表1 超高层建筑截面测压过程遇到的问题与方案
根据表1的解决策略计算出高层建筑截面受到的气压,得到高阶广义气动力谱后,根据显示数值验证横风向气动性能。上述方式在解决时刚性模型表面风压积分测量是一个相对复杂的过程,需要寻找大量测压点与各个管道连接,而超高层建筑表面通常比较复杂,所以在检测过程会划分成多个小区域测量[14]。
1.3 高频动态天平测力
高频动态天平测力是一个矫正过程,利用天平的固有频率计算出中高层建筑受到的横风向气动力。横风向的响应速度和风速成正比,因此利用高频动态天平册立得到的结果准确率很高[15]。由于横风向气动力受到的平均速度难以确定,而且测量点具有离散型,所以必须要进行4-6次的测量,这样才能确保得到的数值的准确性。高频动态天平是上世纪70年代发展而成,在测量时值考虑强迫振动作用,不需要考虑阻尼之间的关系,在锁定截面面积后,将截面分为正方形、矩形和三角形三种形式,记录每个形式的脉动风荷载。建筑物所受的风向气动性能与所处的环境位置也有关,即高层建筑是处于海岸地貌、乡村地貌还是市区地貌对于测力结果都会产生不同的影响。横风向气动力谱的峰值反应所受风力,如果峰值增高,则表示受到的风力增加;如果峰值降低,则表示受到的风力减少。
2 典型截面超高层建筑横风向阻尼识别
在确定典型截面超高层建筑横风向气动力后,对典型截面超高层建筑横风向阻尼进行识别。经过大量实验研究可以发现,当折算风速超过6m/s时,使用气动力谱得到的响应结果要远远小于横风向负气动实验得到的结果,这种误差很容易造成建筑设计上的计算错误,甚至会形成危险建筑物。气动阻尼力随建筑物高度的增加而逐渐锥度化,如图3所示:
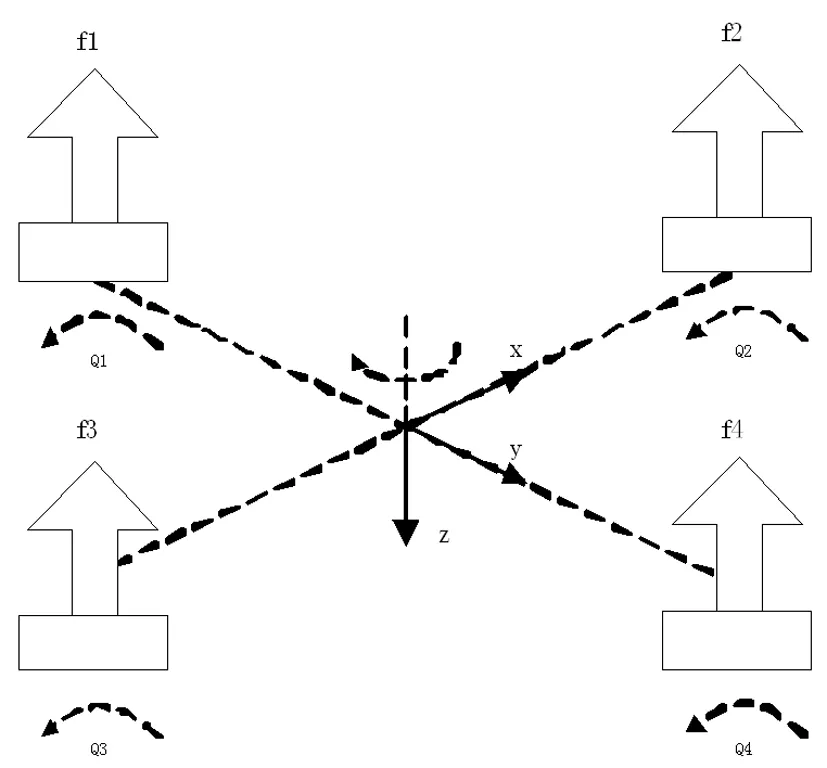
图2 典型截面超高层建筑受到的气流

图3 气动阻尼力的锥度化变化过程
对图3进行具体解释如下:由于在不同高度下,建筑物受到的风荷载力不同,所以气动阻尼力也不同,会随着阶梯收缩而收缩。超高层建筑中存在多个切角,如果切角上受到的气动阻尼力与横风向力不同,则代表截面建筑高层受多个气压影响。立面阶梯很容易与方形截面生冲突,形成漩涡脱落,所以分析气动阻尼力气动阻尼力的锥度化变化过程可以更好地识别横风向气动性能。
计算气动阻尼时需要将刚性模型和气动弹性模型放到一起做统一对比,建立出一个模拟风场,在所建立的模拟风场中分离气动阻尼数值,借助系数参数识别出气动阻尼的输出信息值。系数参数识别是一种随机性很强的方法,在高密度的系数下计算出各个参数,根据模拟状态分析分辨率,如果分辨率降低,则代表超高层截面的风向气动性能计算精度降低。
3 典型截面超高层建筑横风向气动荷载的计算
在不同模型下荷载因子具备的荷载力不同,刚性模型断面形式有如下5种:

图4 刚性模型断面形式
图4中的刚性模型皆为矩形,高度都为300m,在同等压力下测量每个模型的横风向气动荷载,模型1的测量点共有150个,模型2的测量点有200个,模型3的测量点有250个。以此类推,在不同的截面面积下荷载因子会产生不同的荷载力,所以受到的横风向气动力不同,产生的气动性能也不同。
超高层建筑的横风向气动荷载是通过平均风和紊流导致的,计算时可以设置多个荷载因子,根据每个荷载因子在动态和静态下的风荷载来判断气动荷载,假定风场属于B类和D类,两种风场的理论值和实际值完全吻合。在这两类风场中,典型截面超高层建筑受到的横风向紊流度和顺风向紊流度不同,横风向紊流度是顺风向紊流度的70%,而顺风向紊流度能够与气动性能谱较好地融合。横向气流紊流度与建筑物的实际高度满足如下关系:
Gray(rgb(x,y))=(0.1R+0.4G+0.5B)(x,y)
(1)
公式(1)中,R代表建筑物在横向的风速,G表示在高度风速的平均值,B代表竖向风速的平均指数,x代表典型截面超高层建筑横风向气动力值,y代表顺风向气动力值。通过上述公式计算出典型截面超高层建筑横风向气动荷载即Gray。
超高层建筑的截面有多种多样,鉴于研究的复杂性,只能选取典型截面的超高层建筑进行分析。典型截面的横风向气动荷载因子与普通截面的荷载因子相同,换言之,所有普通截面超高层建筑横风向气动性能都是在典型截面超高层建筑横风向气动性能的延伸,通过研究超高层建筑典型截面的横风向气动性能可以分析所有类型超高层进驻横风向气动性能。
4 实验研究
为了检测对典型截面超高层气动性能的研究效果,与传统研究方法进行了对比,针对矩形、正方形和三角形三种截面进行研究,设计了对比实验。
4.1 实验参数设计
实验参数如下表1:
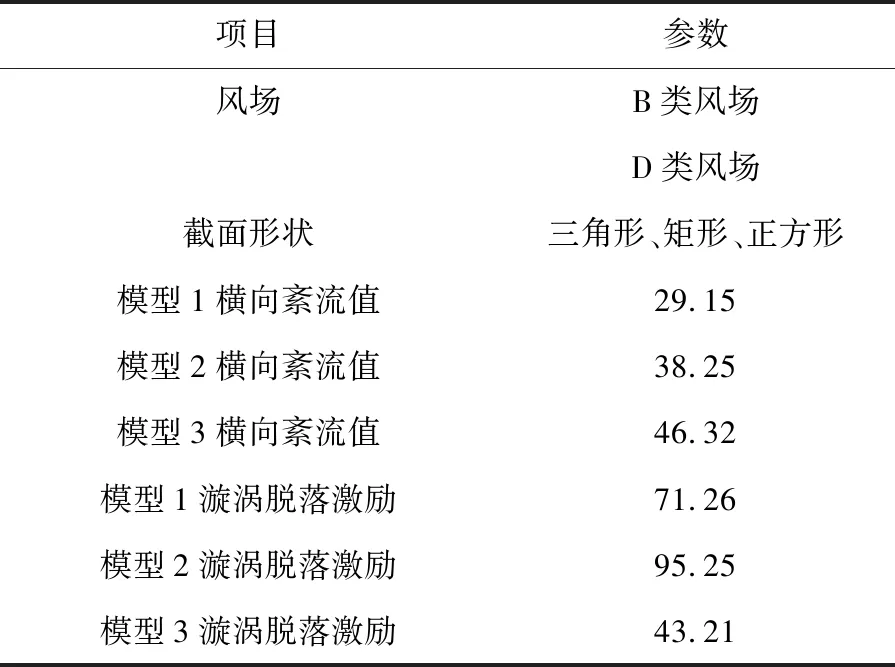
表1 实验参数
4.2 实验过程
根据上述设定的参数进行实验,对正方形、矩形和三角形三种典型截面的高层建筑进行横风向气动性能研究,分别记录在不同截面下传统研究手段和所提方法对气动性能的研究效果,并与实际效果进行对比。
4.3 实验结果与分析
得到的实验结果如下所示。
(1)正方形截面超高层建筑横风向气动性能研究对比实验结果
观察图5,在第一次试验时,超高层建筑正方形截面的实际气动性能值为50,所提方法得到的气动性能值48,传统的研究方法得到的气动性能值80;在第三次试验时,实际气动性能值为22,所提方法得到的气动性能值19,传统的研究方法得到的气动性能值68;在第五次试验时,实际气动性能值为20,所提方法得到的气动性能值20,传统的研究方法得到的气动性能值50。

图5 正方形截面高层建筑气动性能研究
(2)矩形截面超高层建筑横风向气动性能研究对比实验结果
对图6进行分析,在第一次试验时,超高层建筑矩形形截面的实际气动性能值为92,所提方法得到的气动性能值98,传统的研究方法得到的气动性能值58;在第三次试验时,实际气动性能值为52,所提方法得到的气动性能值70,传统的研究方法得到的气动性能值60;在第五次试验时,实际气动性能值为69,所提方法得到的气动性能值71,传统的研究方法得到的气动性能值48。

图6 矩形截面高层建筑气动性能研究
(3)三角形截面超高层建筑横风向气动性能研究对比实验结果
由图7可知,在第一次试验时,超高层建筑正三角形截面的实际气动性能值为58,所提方法得到的气动性能值51,传统的研究方法得到的气动性能值32;在第三次试验时,实际气动性能值为52,所提方法得到的气动性能值48,传统的研究方法得到的气动性能值31;在第五次试验时,实际气动性能值为54,所提方法得到的气动性能值54,传统的研究方法得到的气动性能值28。
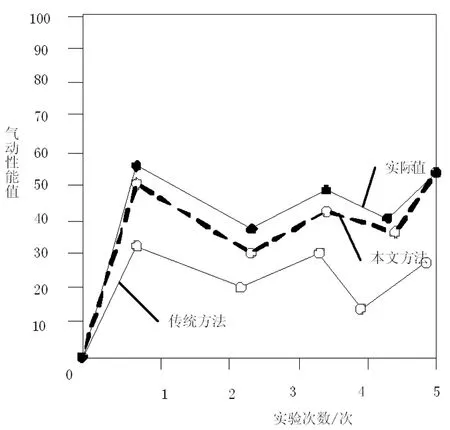
图7 三角形截面高层建筑气动性能研究
4.4 实验结论
根据上述实验结果,得到如下实验结论:超高层建筑受到的横风向性能会随着建筑外形的改变而发生变化。目前研究的高层建筑物主要是针对简单形体的,即标准状态的正多边形,但是在实际工作中,建筑物的横截面往往比较复杂,而且会随着高度的增加而不断收缩,当达到一定高度后,横截面要进行切角处理、穿洞处理等,这样导致截面形状更加复杂。复杂的外形会使建筑物的尾流激励强度增加,空间相关性发生改变。高层建筑物如果缺少深入彻底的研究,很容易出现横风向气动力谱错误的状况。所以在研究气动阻尼时,需要考虑多个因素。如:折算风速、紊流速度、建筑的高度、宽度和长度等,这对于刚性模型和气动阻尼的要求都很高。系统识别是解决上述问题的有效方法,在频域分析中得到多个数据点,结合实际情况分析气动性能。对于不同的响应,荷载能力不同,气动力大小与分布也不同,需要结合具体内容具体分析。
传统的气动性能研究方法缺少成熟度,在测压检测等方面花费的精力较少,从而导致理论值和实际值中间有很大的误差。所提方法针对多种典型截面超高层建筑的气动性能进行分析,不仅能够有效提高准确率,同时也能够降低重现期峰值,确保建筑物的质量。虽然传统气动性能研究方法在某些时刻与实际值较为贴切,但是就整体而言,所提的气动性能理论与实际值的相似度更高,对于建筑高层建筑的帮助更大。
5 结 语
针对上述问题对典型截面超高层建筑横风向气动性能进行深入的研究,通过分析超高层横截面受到的气流判断建筑气动性能,建立多个刚性模型,对每个刚性模型进行具体的分析,给出测量点,根据测量点判断横风向阻尼,最后计算了典型截面超高层建筑横风向气动荷载。所提方法属于理论研究,所提方法对于超高层建筑有积极的促进作用和一定的指导意义,但还缺少实际检测,需要在实践中落实研究的可行性。

