考虑板间土拱效应的斜插桩板墙受力机理研究①

屈俊童， 胡文斌， 吴绍山， 杨 正， 季 东

(云南大学，云南 昆明 650500)

0 引 言

进入 21世纪以来，人们对城市环境、人居环境的要求日益提高，传统桩板墙无法解决绿化的问题日益突出。为了解决这一问题，对传统桩板墙进行改进势在必行。近年来，在昆明市科技局和官渡区科技局的资助下，云南大学和中铁二院昆明勘察设计研究院的研究人员已经对斜插式桩板墙结构桩的结构受力、合理桩间距、桩间土拱效应、板的最优倾角、绿化植物选配等问题进行了相关研究[1～4]。其中，字晓雷等人就斜插桩板墙中钢筋定位问题开展了相关研究[5]；屈林河等人对挂板式斜插桩板墙进行了受理机理研究[6]。但是斜插式挡土板作为整个斜插式桩板墙的一部分，对板的研究显得相对较少，尤其是在板间距变化对板间土拱的强度、墙后土压力分布模式的影响以及如何确定合理板间距等问题上鲜有研究。

以下根据斜插式桩板墙板间土拱的实际受力情况，简化拱体受力，得到合理拱轴线方程以及破坏控制条件，最后在拱轴线基础上对斜插式桩板墙板后土压力公式进行推导，将理论计算结果与吴绍山[7]等人研究的模拟结果进行比较。

1 以“土压力”为原型的合理拱轴线

假设板间存在土拱，按照其实际受力绘制出的受力图如图1所示。

图1 板间土拱实际受力图

在进行受力分析之前，作出如下假设：

(1)在拱体上方产生的土压力q1为相邻两个拱圈之间的一小部分土体构成，与拱后土压力相比可以将其忽略不计，而拱圈内部的土重G与拱圈下部的土反力q2作用方向相反，对拱圈的影响有限，因此也可忽略不计，对于拱后的稳定区，其土压力按主动土压力计算，即ka=tan2(45°-φ/2)；

(2)在拱体稳定时，拱轴线上只存在轴力，无弯矩作用；

(3)拱脚的破坏形式为剪切破坏；

(4)竖向土拱宽度为板长B，土拱厚度近似取挡土板厚度b。

根据以上假设，绘制出的受力简图如图2所示：

图2 板间土拱受力简图

根据受力简图，以下进行竖向合理拱轴线推导，对A点进行取弯矩有：

(1)

可得：

(2)

同理，对拱y方向的力平衡方程Σy=0和对o点进行取弯矩M0=0分别得到：

(3)

(4)

由合理拱轴线任意截面上弯矩为零，可得：

(5)

将FAH代入上式可得拱轴线方程：

(6)

其中：H为相邻板板中心间距，f为土拱拱高。

2 考虑板间土拱效应的土压力计算公式

由于斜插式桩板墙的特殊结构，使其在板间形成竖向土拱，现在以“土压力”为原型的合理拱轴线方程基础上对拱后的水平土压力公式进行推导，并与竖向土压力公式合并，得到垂直于板后的土压力，并与吴绍山[7]等人的数值模拟结果进行比较。挡土板的受力情况如图3所示。

根据上述所得的板间竖向合理拱轴线方程(6)，并根据图1可计算出竖向板间土拱的面积为：

(7)

故水平土压力和水平压应力大小分别为：

(8)

(9)

其中：f为板间土拱拱高。

图3 挡土墙受力情况

l=mod(z,h+d)

(10)

综上所述，挡土板后土压力计算公式为：

p=pysinα+pzcosα

(11)

即：

(12)

其中：α为挡土板倾角，z为桩顶到某一深度的距离，d为板间距，h为挡土板垂直高度，r为土体重度，f为板间土拱拱高，H为相邻板中心距。

3 土压力计算结果对比

根据吴绍山[7]等人所做的数值模拟模型的参数，取挡土板倾角为α=43°，挡土板竖向高度h=0.117m，土体内摩擦角φ=30°，挡土板厚度b= 0.015m,板间距d分别取 0、0.1倍板宽(13.67mm)、0.2 倍板宽(27.35mm)、0.3 倍板宽(41.02mm)、0.4 倍板宽(54.69mm)、0.5 倍板宽(68.37mm)并将土压力计算公式所得板中土压力理论值如表1所示，与数值模拟土压力的Q～s变化对比曲线如图4所示。

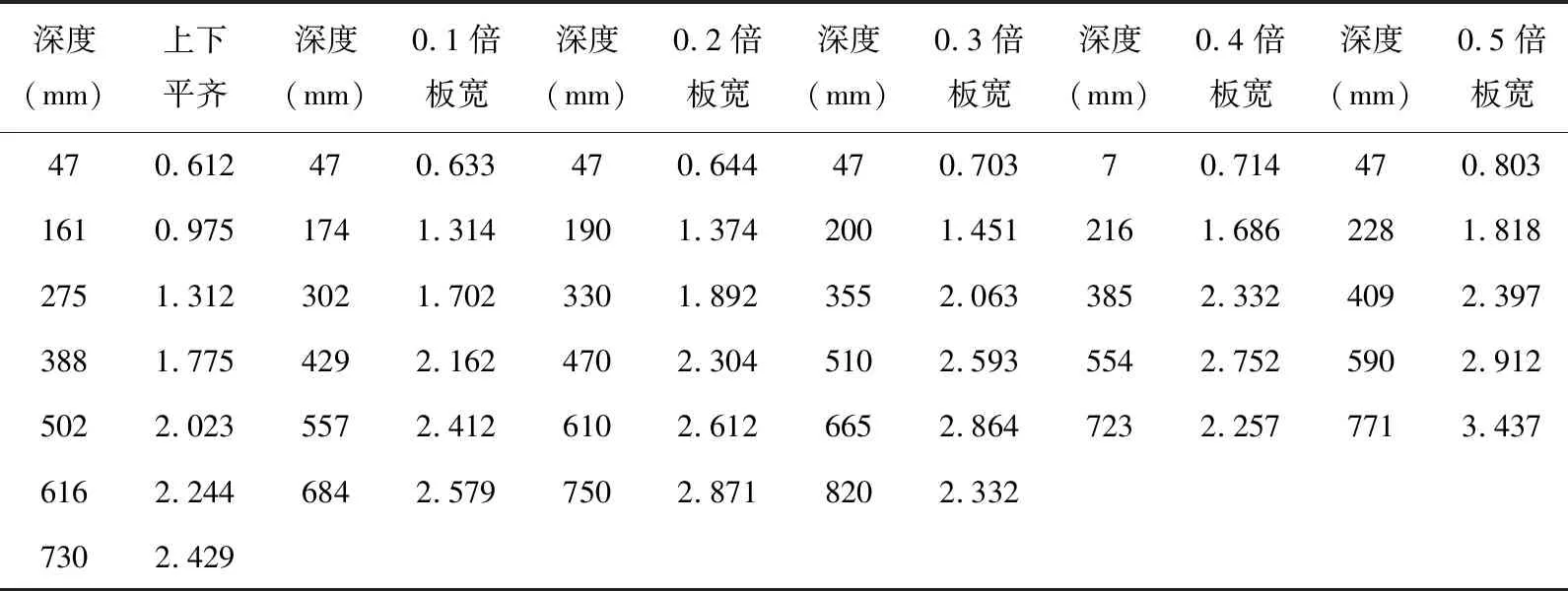
表1 不同板间距下板后土压力理论值(kPa)

图4

从以上对比结果可以看出：所推导出的基于板间土拱效应下的板后土压力计算公式与数值模拟结果基本吻合，也在一定程度上表现出了土压力呈锯齿状分布的特点，且板间距在 0.2～0.4 倍板宽时，包络性较强，因而推导的土压力公式具有一定的参考价值。

4 结 语

根据板间土拱的实际受力情况，提出了相应的假设条件，以“土压力”为原型推导出了板间竖向土拱的合理拱轴线方程，随后，在以“土压力”为原型拱轴线方程的基础上，进一步推导出了板后土压力计算公式，将该公式的理论计算值与数值模拟计算所得土压力随深度变化的Q～s变化曲线进行对比，结果表明，板间土拱存在的情况下，该公式所推导出的土压力随深度的变化曲线包络性较好，在一定程度上表现出了土压力呈锯齿状分布的特点。