考虑反演及桩土相互作用的拟动力试验方法
易伟建+夏玲琼

摘要:考虑桩土结构相互作用,建立整个结构体系试验模型,在土槽试验室模拟框架结构在地震作用下的反应.在考虑桩土相互作用的拟动力试验中,由于下部结构的不可控性和土体的不确定性,提出采用反演分析识别下部结构的动力反应,试验中通过传感器有效获取下部结构状态信息,利用这些测试信息作为反演分析的基础数据,确定桩土工作状态,运用子结构的概念完成整个结构体系的拟动力试验.以某框架为例,采用考虑反演分析的试验方法、等效线性化方法以及刚性地基假设方法,探讨地震作用下结构反应的不同.试验及模拟分析表明,地震作用下,土体较早地进入了塑性阶段,结合反演分析的该试验方法能更好地模拟包括桩土在内的整个体系在地震下的反应.考虑反演分析试验方法的结构顶端位移最大,等效线性化方法次之,刚性地基假设最小;考虑反演分析试验方法的层间位移角和层间剪力最小,固定基础假设最大.
关键词:桩土相互作用;反演;等效线性化;拟动力试验;自由场;钢筋混凝土
中图分类号:TU375.4 文献标识码:A
Inverse Analysis Method for Pseudodynamic
Test with Pilesoil Interaction
YI Weijian, XIA Lingqiong
(College of Civil Engineering, Hunan Univ, Changsha, Hunan410082, China)
Abstract:A new method was proposed for the assessment of frame structure under seismic excitation in the lab with the consideration of pilesoil interaction. In this method, an inverse model was proposed to identify the dynamic response from the substructure, the model, which relates sensor's data to the working state of the piles in the test system, was used to reduce the errors caused by uncontrollable of substructure and uncertainty of soil.Test validation was conducted by an idealized frame structure separately in this model, equivalent linearization method and the rigid foundation assumption. Numerical simulation and the tests data show that, under seismic excitations, the soil would experience plastic stage at the beginning of the excitations, and the new proposed method had a great advantage in the simulation of the pilesoil interaction. For the top displacement in the test structure, maximum displacement was found in the inverse model, followed by the equivalent linearization method, minimum in the rigid foundation assumption; however, for the drift ratio and interstory shear, the former order was inversed.
Key words:pilesoil interaction;inverse model;equivalent linearization method;pseudodynamic test;free field;reinforced concrete
对于采用桩基础的结构物,桩和上部结构的存在会使地基的振动不同于天然场地土的振动[1-2],地基的刚度和阻尼也会影响桩基础和上部结构的受力和变形性态[3-4],同时上覆土层对来自基岩的地震激励具有放大或过滤的双重效应.因此,采用传统抗震设计方法,在假设基础刚性与地基固定连接的情况下,简单地将地基地表反应或基岩地震动自建筑物基础输入,得到的结构振动响应是不准确的[5-6].Stewart等[7-8]用系统验证方法对包含有不同结构类型和地质条件的57种建筑场地进行了多达77个强震记录情形下的土结构体系分析,结果显示,地基越软相互作用对上部结构动力反应影响越大.Lin和Tsaur [9]利用Lotung大比例模型地震观测数据结果,对比验证了采用时域内的考虑非线性土滞回效应的粘弹性地基模型来预测建筑物埋置基础的地震反应的有效性.王开顺等[10]研究对比了1 144组考虑相互作用的基底剪力结果,大部分基底剪力是减小的,但也有一小部分是增大的.可见,按传统的刚性地基假定计算出来的地震作用来进行抗震设计不一定安全.
本文以Penzien等桩土相互作用模型为基础[11], 建立了一种考虑桩土框架结构相互作用的计算模型,下部结构模型如图1所示.该计算模型采用自由场输入.在试验过程中,通过传感器获取下部结构状态信息,利用这些测试信息作为反演分析的基础数据,确定桩土工作状态,实时修正模型中的桩土参数而完成拟动力试验[12].
1试验模型与装置
按照中国规范GB 50011-2010《建筑抗震设计规范》[13],JGJ3-2010《高层建筑混凝土结构技术规程》[14]和GB 50010-2010《混凝土结构设计规范》[15]设计了一栋8层3跨的钢筋混凝土框架结构[13-15].底部两层层高为4.2 m,上部6层层高3 m,房屋结构高度为26.4 m,结构立面图如图2所示.抗震设防烈度为8 度(0.2 g),二类场地,抗震设防等级为二级.该结构混凝土采用C30,纵筋采用HRB400,箍筋采用HPB300,框架梁柱尺寸及配筋见表1.
由于场地条件有限,取底部两层一跨作为试验子结构,尺寸比例为1∶3.试验模型下部结构采用4根打入式无缝钢管桩,外径159 mm,内径147 mm,壁厚6 mm,打入土中深度为3 m.桩身上布置有土压力传感器、倾角仪和应变片,传感器竖向间距为30 cm,布置如图3所示,桩1和桩4为对角的两根桩.整体试验装置如图4所示.
2试验原理
2.1体系动力方程
M+C+KU=-Mg+ChG+KhUG.(1)
式中:M=Ms+Me+Mp;C=Cs+Ce+Cp;K=Ks+Ke+Kp;Ms,Cs和Ks分别为上部结构的质量矩阵、阻尼矩阵和刚度矩阵;Mp,Cp和Kp分别为桩基础的质量矩阵、阻尼矩阵和刚度矩阵;Me,Ce和Ke分别为等价土体系的质量矩阵、阻尼矩阵和刚度矩阵;G和UG分别为自由场地多质点体系的速度向量和位移向量,可以由自由场的动力方程求出;g为基岩处输入的地震加速度向量;,和U分别为质点相对于基岩的加速度、速度和位移向量;Kh和Ch分别为桩土相互作用的水平弹簧刚度和阻尼.
2.2自由场动力方程
MGG+CGG+KGUG=-MGIg.(2)
式中:MG,CG和KG分别为多质点体系的质量矩阵、阻尼矩阵和刚度矩阵;G,G和UG分别为多质点体系的加速度向量、速度向量和位移向量;I为单位列向量;g为输入的地震加速度波.
2.3桩土相互作用的刚度与阻尼
水平弹簧刚度Kh由明德林(Mindlin)公式求解单位水平力作用下不同深度处的桩平面平均位移取倒数得到,由下式给出:
Khi=8πEi3arcsinh hi-ziD+arcsinh hi+ziD+23B2×
D2hi-2D2zi+hiz2i+z3i[D2+(hi+zi)2]1/2-z3i-D2zi[D2+z2i]1/2-
2
3zi-hi[D2+(hi-zi)2]1/2-zi(D2+z2i)1/2+
43D2zi+hiz2i[D2+(hi+zi)2]3/2-D2zi+z3i(D2+z2i)3/2-1.(3)
式中:Ei为第i层土的弹性模量;hi为第i层土的厚度;zi为第i层土中心深度;D为桩半径.
2.4反演过程
由在桩身布置的土压力传感器可以计算得到桩身土压力沿深度的变化,从而计算得到沿桩长的土压力分布.
F0=0,Fi=lBpRi-pLi. (4)
式中:F0为桩底的水平力;Fi为第i点l长范围内桩身所受水平力;B为桩身直径;l为土压力计之间的垂直距离;pRi,pLi分别为第i点左右两侧土压力所测的水平力,测试值为负数时取0.桩身土压力积分可以得到桩身各截面弯矩,桩身截面弯矩求法如下:
M0=0,
Mi=1/2[p1il2]+1/3[p1-p0il2]+…+1/2[pji-j+1l2]+1/3[pj-pj-1×[i-j+1l2]+…+1/2pil2+1/3[pi-pi-1l2]. (5)
式中:M0为桩底的弯矩;Mi为第i点桩身所受弯矩;pi=PRi-PLiB为第i点单位长度桩身所受水平力.
根据桩身布置应变片的测试数据,计算得到各截面曲率.根据各点曲率,计算桩身截面各点的倾角和位移.
计算各点曲率:
φi=εRi-εLi/B. (6)
式中:φi为柱在i点的曲率;εRi,εLi分别为桩在i点左右两侧的应变量.
由曲率沿长度积分可以得到桩上各测点弯曲角度,假设在各应变片之间曲率均匀变化,则
θ0=0,θi+1=θi+1/2φi+φi+1l. (7)
式中:θ0为桩身底部转角,假设为0;θi为桩身第i点的转角.
也可由桩身布置的倾角仪,直接得到弯曲角度.弯曲角度沿长度积分可以计算得到桩各点水平位移:
u0=0,
ui+1=ui+θil+1/3il2+1/62i+1.(8)
式中:u0为桩身底部水平位移,假设为0;ui为桩身第i点的水平位移.
已知桩身各截面弯矩和曲率,可以计算出桩身截面刚度;根据桩身水平方向受力和桩身水平位移,可以计算得到桩土相互作用水平弹簧刚度.试验过程中桩变形较大的时候,桩身截面刚度和土的力学特征都将发生变化,因此试验过程中可以用反演得到的桩身截面刚度和桩土相互作用水平弹簧刚度修正模型中的相应参数.
试验中桩身弯曲截面刚度及桩土相互作用的水平弹簧刚度可用下式计算:
EI=ΔM/Δk=Mni-Mn-1i/ni-n-1i; (9)
Kni=ΔF/Δu=Fni-Fn-1i/uni-un-1i. (10)
式中:EI为桩身刚度;Mni为第i点第n步桩身弯矩;ni为第i点第n步桩身曲率;Kni为第i点第n步桩身刚度;Fni为第i点第n步桩身所受水平力;uni为第i点第n步桩身水平位移.
2.5试验流程
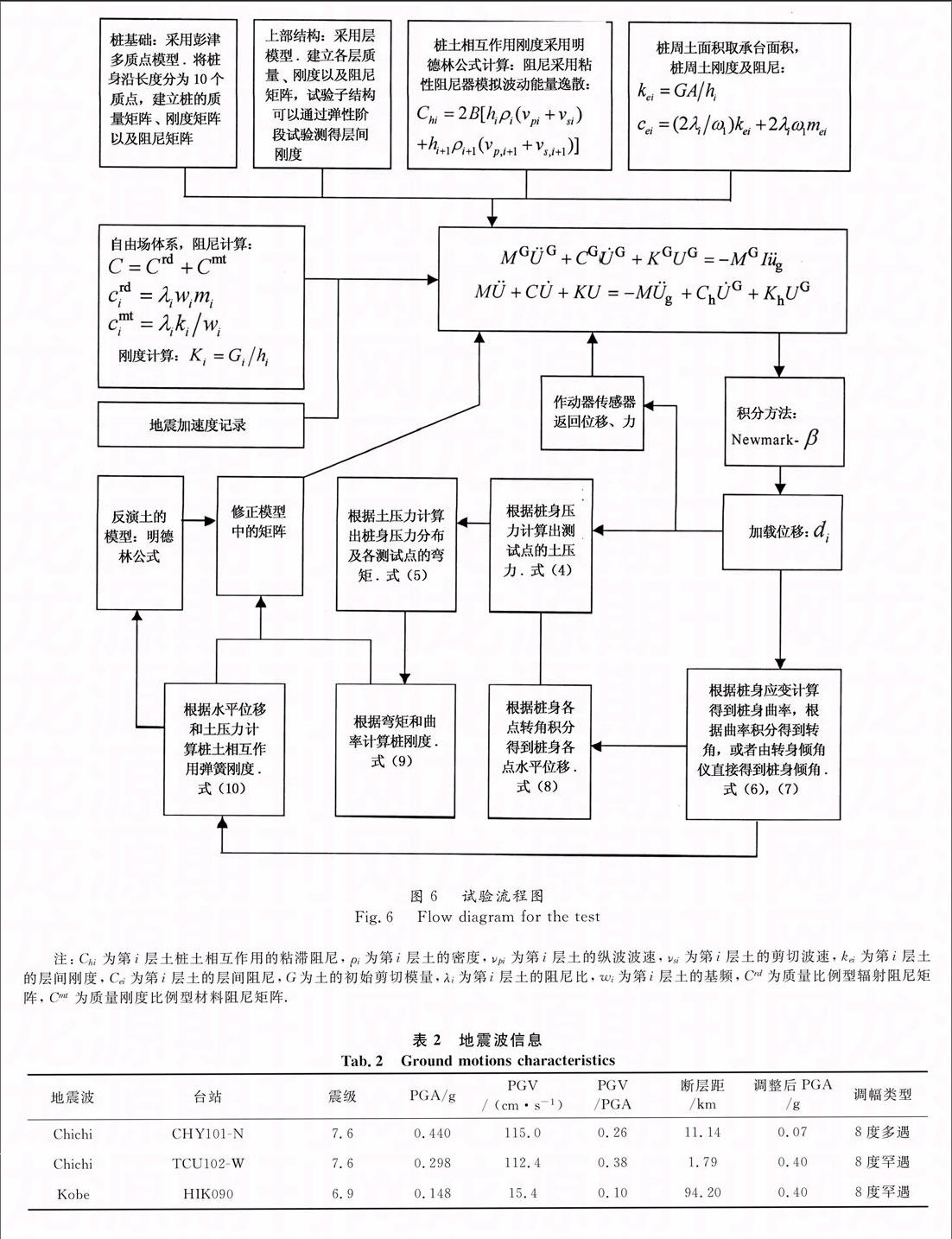
图5为试验数据传输示意图.试验过程中采集的测试数据通过接口函数传入拟动力试验程序,试验程序通过接口程序与系统的控制程序交换数据,控制程序通过控制器控制作动器在结构上实现位移加载.图6为整个基于反演的拟动力试验算法的流程图.
3试验结果与分析
3.1试验方法
利用前面所述的计算模型,针对试验所设计的结构,选用了如表2所示的3组地震加速度波作用.为了对比与验证本文试验方法,采用以下3种方式对结构进行非线性分析及试验.
1)采用文献[16-17]提出的等价线性化方法来考虑土体的非线性滞回性质.该方法通过一系列线性运算多次迭代以得到土体非线性动态响应的近似解.利用此近似解,采用有限元计算方法,得到结构在相应地震加速度记录下的响应.以下简称此方法为方法1.
2)采用图6所示试验方法在土槽进行拟动力试验.以下简称方法2.
3)针对试验所设计的结构,假设基础为刚性基础,选用表2所示地震波,利用OpenSEES程序对其进行非线性动力分析.以下简称方法3.
试验所在土槽的土体初始物理参数、试验子结构的初始刚度测试、试验装置以及试验现象,作者将在另外的文章中详细描述,在此不再赘述.
3.2试验现象
第1组地震波为近场地震加速度波,加速度幅值调至0.07 g,相当于8度多遇地震.在此类加速度记录作用下,结构底层柱和二层柱根部以及底层和二层梁中塑性铰转移处产生较明显的弯曲裂缝,试验结束后,结构基本复位,裂缝基本能够闭合.就结构整体而言,未产生影响到结构安全破坏的程度.
第2组地震波为近场地震加速度波,加速度幅值调至0.4 g,相当于8度罕遇地震.在此类加速度记录作用下,在结构梁中塑性铰转移处产生明显弯曲裂缝.柱端产生较明显的弯曲裂缝和弯剪斜裂缝,并且底层柱根斜裂缝往上发展,部分沿着柱纵筋往上发展,导致钢筋与周围混凝土之间的粘结开裂.与此同时,节点核心区域出现沿对角线方向的斜裂缝.试验结束后,大量裂缝不能闭合,结构发生较大倾斜.
第3组为普通中远场地震加速度波,加速度幅值调至0.4 g,相当于8度罕遇地震.
在此类加速度记录作用下,结构底层柱和二层柱根部以及底层和二层梁中塑性铰转移处产生较明显的弯曲裂缝,而且底层柱根部裂缝进一步发展形成弯剪斜裂缝.试验结束后,结构基本复位,部分裂缝能够闭合.就结构整体而言,结构未产生影响到结构安全甚至倒塌的严重破坏.
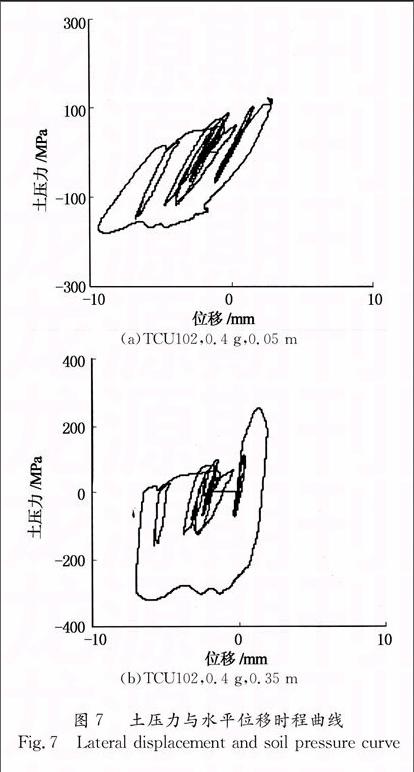
桩上传感器采集到了加载每步桩土状态的数据,图7为Chichi TCU102地震加速度记录作用下,桩基分别为0.05,0.35 m深处土压力数据.在加速度峰值为0.4 g的近场地震记录作用下,土体较早进入了非线性状态,可见采用弹性假设计算是不准确的.本文所设计的试验程序通过实时获取桩土数据,确定桩土状态,并修正动力方程中的桩土相关参数,所以可以更加准确地反映系统实际状态,从而得到更加准确的试验结果.
3.3试验结果对比
表3为计算结果和试验结果对比表,为了对比方便,全部转换为原设计结构的尺寸比例.从表3可以看出,考虑桩土结构相互作用对结构反应的影响主要体现为增大了结构的顶端位移,同时也减小了底层层间位移角和底部剪力.与假定基础刚性的计算结果相比,以Chichi TCU102W地震加速度波作用为例,考虑桩土结构相互作用的试验结果中结构顶端位移增大接近200 mm,层间位移角平均减小约37%.
(a)TCU102,0.4 g,0.05 m
(b)TCU102,0.4 g,0.35 m
对于本文设计的结构,方法2对比方法1,虽然结构的底层层间位移角减小了约10%,但是结构顶端位移增加了225 mm,而这将大大增加结构所受弯矩的二阶效应,对结构非常不利.
考虑土结构动力相互作用的结构顶端水平位移是由基础水平位移、基础转动和上部结构变形3部分组成的.根据桩上及承台上布置的传感器得到的测试数据,对比采用等效线性化及有限元方法计算得到的下部结构变形数据,如表4所示.考虑下部结构反演的拟动力试验方法得到的基础水平位移较大,并且试验中测得了基础的转角,而基础的转角对结构顶点位移影响较大.
综合上述对比分析结果,影响3种方法作用下结构响应不同的原因主要体现在以下两方面:其一,地基土状态的变化,地震加速度作用下,由于土体较早进入非线性阶段,计算模型难以准确地反映土体的状态,只能按照设置的模型进行计算,与试验方法中传感器测试得到的数据有较大的不同;其二,地基土的非线性状态使土结构系统的固有频率和振型都发生改变,一般来说,桩土相互作用将延长结构的
自振周期[18-19].上述两点说明了桩土相互作用对结构动力特性的影响,因此,结构的地震反应必将有所改变.
4结论
1)提出了采用反演分析识别下部结构的动力反应,试验中通过应变片、倾角仪、土压力计等传感器获取下部结构状态信息,利用这些测试信息作为反演分析的基础数据,确定桩土工作状态,运用子结构的概念完成了整个结构体系的拟动力试验.结合反演分析和测试技术,发展了考虑土结构动力相互作用的结构抗震拟动力试验方法,完善了土结构动力相互作用的反演算法,为进一步研究积累了基础数据.
2)通过采用考虑反演的拟动力试验数据与采用刚性地基假设的理论计算结果对比,发现试验测试所得的结构顶端位移较大,同时层间位移角和底部剪力较小.
3)相对于基础固定的情况,阻尼和振型的不同使桩土结构系统的动力特性发生了变化.与刚性地基假设计算结果相比,结构顶点位移相应地增大,基础的变形,尤其是基础转角将较大地增加结构的顶点位移.若结构的底部层间位移角是减小的,则底部剪力和层间剪力一般也是减小的.
参考文献
[1]高爽.高层建筑与桩土共同作用的抗震性能分析[D].北京:中国石油大学储运与建筑工程学院,2010:1-11.
GAO Shuang. Seismic behavior analysis of high rise structure under soilpilesuperstructure interaction[D].Beijing:College of Pipeline and Civil Engineering, China University of Petroleum,2010:1-11. (In Chinese)
[2]KOLEKOVA Y, SCHMID G. Advantages of an analysis of soilstructure interaction in a frequency domain[J].Slovak Journal of Civil Engineering, 2012,19(4):12-17.
[3]LIANG J W, FU J, TODOROVSKA M I, et al. Effects of the site dynamic characteristics on soilstructure interaction (I):incident SHWaves[J]. Soil Dynamics and Earthquake Engineering,2013,44: 27-37.
[4]张盼盼.大型渡槽结构的抗震计算的模型简化[D].长沙:湖南大学土木工程学院,2011: 27-45.
ZHANG Panpan. Model simplification for seismic calculation of aqueduct structure[D].Changsha:College of Civil Engineering , Hunan University,2011:27-45. (In Chinese)
[5]MYLONAKIS G, GAZETAS G. Seismic soilstructure interaction: beneficial or detrimental?[J]. Journal of Earthquake Engineering, 2000, 4(3): 277-301.
[6]PRISHATI R, POONAM S. Effect of nonlinear soilstructure interaction on seismic response of lowrise SMRF buildings [J]. Earthquake Engineering and Engineering Vibration, 2012, 11(4): 541-551.
[7]STEWART J P, FENVES G L, SEED R B. Seismic soilstructure interaction in buildings.I: analytical method[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1999,125(1):26-37.
[8]STEWART J P, FENVES G L, SEED R B. Seismic soilstructure interaction in buildings. II: empirical findings[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1999, 125(1):38-48.
[9]LIN B C, TSAUR Y L. The seismic response of structurevisoelastic foundation systems in time domain and power spectra[J]. Engineering Structure, 1997, 19(12): 977-987.
[10]王开顺,王有为,李林有. 土与结构相互作用地震反应研究及实用计算[J]. 建筑结构学报, 1986, 7(2): 64-76.
WANG Kaishun,WANG Youwei,LI Linyou.Seismic response of soilstructure interaction and its practical calculation[J]. Journal of Building Structures, 1986, 7(2): 64-76.(In Chinese)
[11]PENZIEN J,SCHEFFEY C F,PARMELEE R A.Seismic analysis of bridges on long piles[J].Journal of the Engineering Mechanics Division,1964,90(3):223-254.
[12]易伟建,夏玲琼. 近场地震下考虑桩土框架结构相互作用的拟动力试验[J]. 土木工程学报, 2014, 47(4): 1-8.
YI Weijian,XIA Lingqiong.Pseudo dynamic experimental analysis with pilesoil interaction in nearfault earthquakes[J]. China Civil Engineering Journal, 2014, 47(4): 1-8.(In Chinese)
[13]GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010:20-38.
GB 50011-2010Code for seismic design of buildings[S].Beijing: China Architecture & Building Press,2010:20-38.( In Chinese)
[14]JGJ3-2010高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2010:44-71.
JGJ3-2010Technical specification for concrete structure of tall building[S].Beijing:China Architecture & Building Press,2010:44-71.(In Chinese)
[15]GB 50010-2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010:31-68.
GB 50010-2010Code for design of concrete structures[S] . Beijing:China Architecture & Building Press,2010:31-68.(In Chinese)
[16]曹资, 王松涛. 现代抗震设计方法[M]. 北京: 中国建筑工业出版社, 1997:105-137.
CAO Zi, WANG Songtao.Modern seismic design method[M].Beijing: China Architecture & Building Press,1997:105-137.(In Chinese)
[17]HARDIN B O, DRNEVICH V P.Shear modulus and damping in soils: design equations and curves[J].Journal of the Soil Mechanics and Foundations Division, 1972, 98(7): 667-692.
[18]TSAI N C.Modal damping for soilstructure interaction[J].Journal of the Engineering Mechanics Division,1974,100(2):323-341.
[19]NOVAK M,HIFNAWY L E L.Effect of soilstructure interaction on damping of structures[J].Earthquake Engineering and Structure Dynamic,1983,11(1):595-621.

