基于Info—Gap决策的结构抗震稳健性优化设计
唐和生+范德伟+李大伟+薛松涛


摘要:针对结构抗震设计中存在严重不确定性问题,基于Info-Gap理论建立一种考虑地震设计谱参数不确定的结构抗震稳健性优化设计方法.该设计方法采用Info-Gap模型来描述地震设计谱中反映地面运动强度的水平地震影响系数最大值αmax和场地特征周期Tg的不确定,通过嵌套优化使结构设计满足结构的临界性能要求的同时实现最大化不确定的稳健性.通过对一个6层3跨的钢框架的抗震稳健性优化设计验证分析表明:这种基于满足性能的结构抗震设计需在满足结构性能需求和提高不确定稳健性之间进行权衡取舍;同时也证实该方法为在不易得到不确定性因素足够信息情况下的基于性能结构抗震可靠性设计提供了一条新思路.
关键词:Info-Gap理论;不确定;稳健性;抗震设计
中图分类号:TU318;TU323.5 文献标识码:A
Info-Gap Decision for the Robust Seismic
Design Optimization of Structures
TANG He-sheng1, 2, FAN De-wei2, LI Da-wei2, XUE Song-tao2,3
(1.State Key Laboratory of Disaster Prevention in Civil Engineering, Tongji Univ, Shanghai200092, China;
2. Research Institute of Structural Engineering and Disaster Reduction, Tongji Univ, Shanghai200092, China;
3. Dept of Architecture, Tohoku Institute of Technology, Sendai982-8577, Japan)
Abstract:Seismic design for buildings is usually subject to various uncertainties, often severe, which have the potential to undermine engineering decisions. It is crucial that these uncertainties be accounted for in seismic design. We formulated a performance-based seismic design model that takes into account uncertainty in the seismic design spectrum of the αmax and Tg. We used info-gap theory for satisfying the critical performance requirements, while at the same time maximized the robustness to uncertainty through nested optimization. The design implications of this robust-satisfying approach were demonstrated with a three-span six-floor steel frame design example. It is shown that design preferences depend upon the performance requirements considering the trade-off between robustness to uncertainty. Also, the result reveals that the proposed method provides a novel tool for the performance-based seismic reliability design under the lack of knowledge.
Key words:Info-Gap theory; uncertainty; robust; seismic design
结构抗震设计中涉及到很多不确定的因素,如中国现行规范中的设计反应谱便是通过对大量实际地震记录的反应谱进行统计分析,并结合工程经验判断后得到的平均谱,以地震影响系数的形式给出.建筑结构的地震影响系数应根据烈度、场地类别、设计地震动分组和结构的自振周期以及阻尼比等确定.而对于给定的结构,其自振周期和阻尼比通常是确定的,进而可直接由抗震设防烈度和场地特征周期来确定地震影响系数的取值[1].由此可知,规范中的反应谱主要取决于反映地面运动强度的地震影响系数最大值αmax和场地的特征周期Tg.而地震影响系数最大值αmax和场地特征周期Tg会因震源机制、传播途径特性及局部地质土质条件等不同而存在着一定幅度的变化,并不是一个确定的值.再者由于规范反应谱的统计值会受到统计分析所用资料的完备性、计算回归过程中数据的离散性以及各种人为的主观性的影响,使得αmax和Tg的取值都是不确定的.
目前不确定性的结构优化设计主要采用的概率和模糊方法都依赖于大量的统计数据,并需要对概率分布或隶属度进行主观假定.研究表明概率模型参数的小偏差可导致结构可靠性计算出现较大误差[2-4].然而,很多结构工程统计样本的采集相对比较困难,难以得到不确定参量的足够信息来确定其概率密度分布,只能得到其幅度或界限.因此,以概率方法为代表的不确定优化方法并不完全适用于结构工程领域[5].
20世纪90年代,Ben-Haim[2]和Elishakoff等人[6]提出并倡导应用凸集合模型描述区间不确定性.凸集合模型仅需要少量不确定性参数的统计信息,特别适用于严重不确定的优化设计.Ben-Haim在文献[7]中基于凸集合理论,提出了非概率可靠性的思想:若系统能容许不确定参量在一定范围内的波动,则认为系统是可靠的,并指出结构可靠性可以用结构在失效前能够承受的不确定性总量来度量.在结构设计方面,文献[8-9]基于凸模型将非概率可靠性理论应用于结构设计.苏永华等[10]基于区间数学理论,建立了深部工程围岩力学参数及其对开挖响应的区间非概率分析模型.但是当不确定性参数采用区间数或凸集合描述时,由于复杂结构情形的可靠性问题通常所呈现的非凸特性给此类方法带来了分析计算上的困难,而且区间算法可能引起扩张,从而使该方法的应用受到较大限制.
在凸集合理论研究的基础上,Ben-Haim提出了“严重不确定性”的概念,即仅能获知不确定性参数假定的名义值,但无法获得不确定性参数其他信息的情况;并针对这类问题创立了Info-Gap决策理论(Info-Gap Decision Theory, IGDT)[11].IGDT作为一种考虑严重不确定性的非概率优化方法,已经成功地应用于各个领域,包括神经网络[12]、生物保护[13- 14]、金融经济[15]等.一些学者也尝试将IGDT应用于结构工程领域中[5, 16],但这些研究都仅限于结构的稳健性函数解析求解简单问题,对复杂的嵌套优化问题则鲜有涉及.鉴于此,本文提出了一种将IGDT与自然计算方法相结合的优化方法,应用人工智能算法来处理IGDT的嵌套优化问题,并将该方法应用于基于性能的结构抗震优化中.最后通过一例钢框架结构的抗震性能优化设计,验证该方法处理基于性能的抗震稳健优化设计的有效性.
1 Info-Gap不确定稳健性优化模型
基于非概率Info-Gap不确定模型的结构稳健性设计是一种满足性能的优化设计,其目的是设计出满足所有约束条件及临界性能的稳健性最优的结构.其基本思想为:首先选择一个合适的临界性能作为约束,然后在保证结构系统正常工作的前提下,最大化结构系统抵抗不确定变量波动的能力,该模型主要由以下几部分组成.
1)设计变量:在结构优化设计中,首先是确定设计变量以达到理想设计的结构性能或其他目标.可以表示为:
q = [ q1, q2, …, qn ]T , qmin ≤q≤qmax . (1)
式中:n为设计变量的个数;qmin, qmax分别为设计变量的下限与上限.在结构优化设计中,设计变量包括几何尺寸、形状或结构拓扑等结构设计参数.
2)不确定变量:在结构设计中,除设计变量外,还存在一些不确定变量.这些不确定变量u来源于许多方面,如外荷载、边界条件、几何参数以及材料参数等.图1为一简单的Info-Gap模型,假定不确定变量的名义值为,而其真实值u未知,这两者之间存在的差距以α来表示,且这种差距的程度是未知的.Info-Gap不确定模型将α称为不确定性水平.
3)约束条件:通常结构设计问题还必须考虑约束条件,以满足设计变量空间的可行域要求.约束条件的表达式为:
gi(q)≤0,i=1,2,…,I. (3)
式中:I为约束条件的个数.结构设计中,约束条件通常需要考虑应力约束和位移约束等.
4)性能函数:性能函数R(q, u) 是设计变量q和不确定变量u的函数,代表结构性能指标或响应.性能函数可以是结构造价、材料体积或结构质量,也可以是结构柔度、节点位移、应力、自振频率或屈曲荷载等结构性能.临界性能rc为性能函数R(q, u)必须满足的前提条件.这两者构成了非概率Info-Gap稳健性设计过程时必须满足的临界性能条件(假设性能函数必须小于临界性能rc):
R(q,u)≤rc. (4)
通常情况下,性能函数是设计变量与不确定变量的隐函数,需要通过结构分析(如有限元分析)来计算.
5)稳健性函数:传统的优化设计是将性能函数R(q, u)作为目标函数,以实现性能最优化的结构设计.而基于Info-Gap的结构稳健性优化设计的目的是在满足临界性能条件下最大化不确定性水平αi.数学表达式如下:
i(q,rc)=max {αi:(max R(q,u)≤rc)},
i=1,2,…,I.(5)
式中:I为设计中所需考虑的不确定性水平的个数,当存在多个不确定性水平时,基于Info-Gap模型的结构稳健性设计转变为多目标设计.稳健性i是第i个不确定性水平αi的最大值,即结构在满足约束条件及临界性能条件下所能承受的不确定变量实际值偏离其名义值的最大极限.
2基于Info-Gap理论的结构抗震性能稳健
性优化设计
传统的性能优化设计将结构的性能指标作为优化目标,例如得到造价最小的结构设计.在不确定性结构设计中,以概率方法为代表的性能优化设计需要足够充分的统计样本,或对不确定性参数进行经验假设,难以建立不确定性参数信息严重缺失的结构设计模型.为解决此类问题,本文基于Info-Gap模型[11]以稳健性函数来表示结构系统的最大非概率不确定性水平,建立最大化稳健性函数的结构稳健性设计策略及优化方法,将稳健性函数的最大化问题转化为考虑约束条件的嵌套优化问题,并采用人工智能算法处理稳健性函数的嵌套优化问题.
如上所述,基于Info-Gap理论的结构抗震性能稳健性优化设计的过程就是通过公式(5)的嵌套优化来求解稳健性函数.该优化过程包括外优化和内优化两个部分,外优化的目标是求解稳健性函数,内优化的目标是求解满足临界性能条件的最不利性能函数.嵌套优化的复杂程度远大于单一的优化过程,这使得精确计算结构稳健性函数变得非常困难.因此,很多学者转而研究可行的数值优化问题.在Info-Gap模型的发展过程中,也是将不确定性问题假定为满足凸集合条件下的不确定性问题,并针对稳健性函数和其他部分提出了相应的计算方法.但是在结构优化中,结构不确定性参数采用区间数或凸集合描述时,结构响应值域通常是非凸的,且具有不止一个局部极值点[17].因此,实际结构的不确定性优化问题相对于单一的优化问题来说更需要采用全局优化方法.
遗传算法(GA)[18]是模拟生物自然进化机制的随机优化方法,它借用了仿真生物遗传学和自然选择机理,通过自然选择、遗传、变异等作用机制,实现个体的适应性的提高,末代适应性最高的个体作为近似最优解.GA对设计变量特殊编码,其寻优搜索由适应度值为引导,对不可微以至不连续的函数优化,GA能以较大概率求得全局解;具有较强的鲁棒性、全局收敛性、隐含并行性及广泛的适应性;并且能处理不同类型的优化变量(离散的、连续的和混合型的);直接搜索法不需要任何辅助信息,对目标函数和约束函数也没有任何要求.由于上述优点,GA在众多学者的努力下已经发展成为一种自组织、自适应启发式概率性搜索优化技术,能有效地求解属于NPC(不可计算的)类型的组合优化问题及非线性多模型、多目标的函数优化问题,从而得到了多学科的广泛重视.GA开始渗透到自适应行为、人工智能、神经网络[19]、机器人、运筹学等学科[20-21],并逐渐扩展到工程技术、计算机科学、管理科学和社会科学等领域[22].基于上述优点,本文采用GA来实现基于Info-Gap的结构抗震性能稳健性优化的计算.
2.1 Info-Gap结构抗震性能稳健性设计步骤
基于Info-Gap结构抗震性能稳健性设计的GA算法主要步骤如下.
1) 开始外优化:设置GA算法参数,确定临界性能rc,在可行空间内初始化设计变量q;
2) 开始内优化:初始化不确定变量u;
3) 以设计变量q和不确定性变量u进行结构分析,求解性能函数R(q, u);
4) 更新不确定性变量u;
5) 返回3),直至达到内优化最大迭代代数;
6) 输出当前满足临界性能条件的最不利性能R(q, u)及相应的不确定变量u;
7) 更新设计变量q;
8) 返回2),直至达到外优化最大迭代代数;
9) 输出当前稳健性函数及相应最优设计变量.
结构稳健性设计过程中,嵌套内优化和外优化分别需要计算性能函数R(q, u)与不确定性水平αi的极值,极值的求解通过GA来实现.在本文中定义不确定性水平u为抗震设计反应谱中的水平地震影响系数最大值αmax和场地特征周期Tg.定义内优化性能函数为结构的最大层间位移角θi,max(q, u).
2.2 抗震性能优化设计中性能函数的求解
本文采用基于文献[23]中μ-ξy-T关系的延性需求谱法而开发求解钢框架地震性能指标的程序,求解结构性能点的位移和层间位移角,求解步骤如下.
1) 求解结构的动力特性:周期T以及振型Φ,其中振型以顶点幅值为1进行标准化.
2) 对第一阶模态,建立结构的pushover曲线.将pushover曲线等效为二折线型,并求得等效单自由度(ESDOF)的周期Te与屈服位移Δy.
3) 根据弹性加速度与位移之间关系求解等效单自由度体系的需求位移Sde并与Δy相对比:①若Sde< Δy则说明单自由度体系尚处于弹性状态,即Sde就是等效单自由度体系的最大响应位移Δu;②若Sde>Δy则说明单自由度体系在该水准下已处于弹塑性状态,利用文献[23]中μ-ξy-T关系求解延性系数μ,进而求解单自由度体系最大响应位移Δu.
4) 利用Δu=φTMφφTMΔu求解结构顶部最大位移,再根据标准化振型Φ求解各楼层最大位移Δi,max,计算楼层最大位移角θi,max.
通过上述介绍,基于Info-Gap理论的结构抗震性能稳健性优化设计流程如图2所示.
3算例分析
3.1模型及算法描述
本文算例为一个6层3跨钢框架结构的抗震稳健性优化设计.设计资料如下:跨度7.5 m,首层层高4.5 m,其余层高3.9 m,抗震设防烈度7度,场地类别一组三类场地.在本文优化中首先对梁柱进行编组,柱子分组为C1~C12,梁分组为B1~B6,单榀框架模型如图3所示.
采用本文算法在满足最大层间位移角小于2.0%前提下,实现钢框架总质量最小并且抵抗的地震影响系数最大.本文优化部分采用MATLAB嵌套DRAIN编程进行结构抗震性能优化设计,在设计中将3D3S的H型钢库截面尺寸定义为设计变量并对其进行编码以便在优化设计中调用.GA算法参数选取如下:群体规模pop=50;最大迭代进化代数gen=150;因为搜索空间是离散变量,所以采用正整数编码,模拟二进制编码;选择方法采用轮盘赌法;交叉方法采用多点交叉,交叉概率pc=50%;变异方法采用非均匀变异,变异概率pm=10%.约束采用限定搜索空间与罚函数相结合的方法,首先限定解搜索空间为柱选用宽翼缘H型钢,梁选用窄翼缘H型钢.分析程序的参数如下:以位移控制,每次位移增加push step=2.5 cm;材料参数:屈服后的强度比SHR=0.03;屈服强度Fy=398 MPa;考虑P-Δ效应.
3.2考虑αmax不确定的稳健性抗震优化设计
将αmax作为不确定变量,性能函数R(X,u)为结构层间最大位移角θi,max.将水平地震影响系数最大值αmax对于名义值max 所增大的百分比定义为模型的稳健性,数学表达式如下:
Πα,max =αmax :αmax -max max ≤α,α≥0.(6)
对应地将式(6)中α定义为稳健性指标,框架总质量随αmax稳健性指标变化,如图4所示.
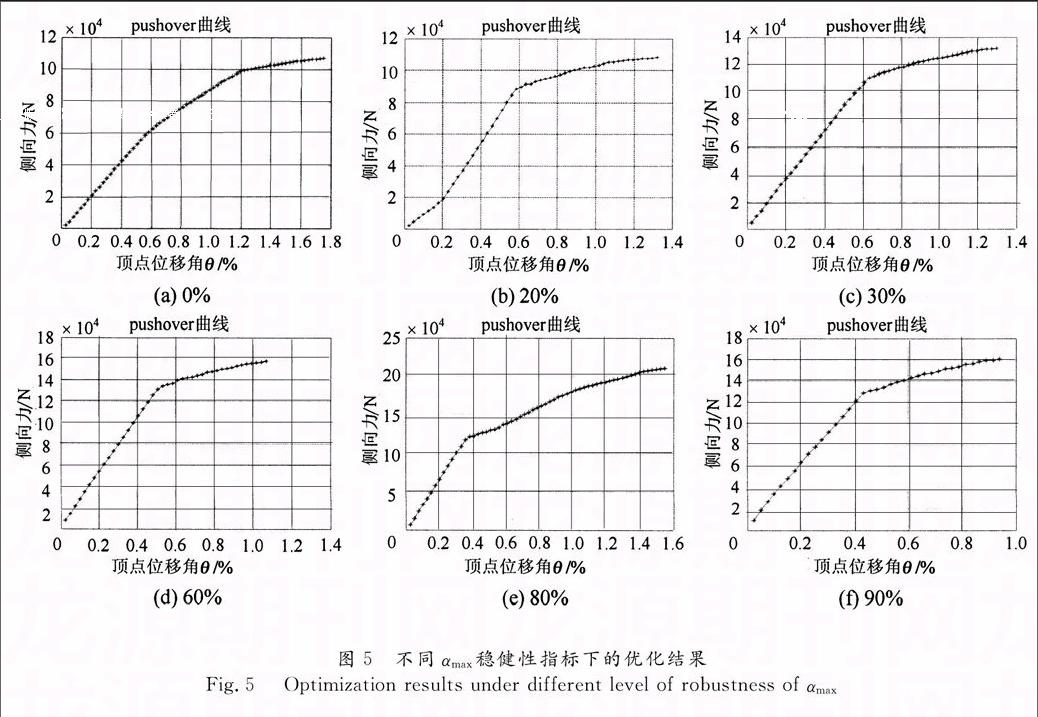
将图4对应①~⑥不同稳健性指标的反映顶点位移角和侧向力关系的pushover曲线列于图5(a)~5(f) 中,并将对应的框架整体特性列于表1中(其中T为结构的自振周期,M为结构的质量,θi,max为pushover分析中结构最大层间位移值).
由表1可知,反映αmax稳健性指标越高所需要钢材质量越大,稳健性指标为30%时,需要的钢材质量要增加17.68%,稳健性指标为80%时,需要增加的钢材质量为40.05%;结构自振周期随αmax稳健性的增高而减小,这也说明随着αmax的增大可通过增大结构的刚度抵抗地震作用.
3.3考虑Tg不确定的稳健性抗震优化设计
将Tg作为不确定变量,性能函数定义与3.2节中相同.将Tg对于名义值g波动幅度值(百分比)定义为稳健性指标α,数学表达式为:
Πα,g=Tg:Tg-gg≤α,α≥0. (7)
框架总质量随Tg稳健性指标变化,如图6所示.
将图6中对应①~⑥不同稳性指标的反映顶点位移角和侧向力关系的pushover曲线列于图7(a)~7(f) 中,并将对应的框架整体特性列于表2中(其中T为结构的自振周期,M为结构的质量,θi,max为pushover分析中结构最大层间位移值).
由表2可知,场地周期不确定性的稳健性指标越大,需要的结构质量越大,说明要抵抗场地周期不确定需要更大的结构质量,如稳健性指标为40%时,需要增大6.29%的结构质量,而当稳健性指标为80%时,则需要增大12.49%的结构质量.
3.4两种不确定性稳健性优化对比分析
图8为两种稳健性优化结果对比图.由图8可知,同等地震作用条件下稳健性指标为0时,两点基本重合,随稳健性指标的增大两条曲线逐渐分离开来,其中地震影响系数的稳健性指标增大引起优化质量增加得更快;从图8中还可以看出,地震影响系数不确定对结构质量的影响相对于场地周期不确定性对结构质量的影响要大得多.
4结论
本文将Info-Gap 决策理论引入基于性能的结构抗震优化设计中,建立了基于Info-Gap 决策的结构稳健设计优化模型,采用GA实现该模型的嵌套优化问题.分别就考虑水平地震影响系数最大值αmax和场地周期Tg不确定性进行了钢框架稳健优化设计分析,通过对6层3跨框架分析表明:反映水平地震影响系数最大值αmax和场地周期Tg不确定性的稳健性指标越大所需要的钢材质量越大.结构设计师和业主可根据自己的要求选择合适的构件组合,付出的代价就是要通过增加结构的质量抵抗αmax不确定和Tg不确定性.通过两种稳健性设计的对比可以看出,αmax不确定对结构质量的影响相对于Tg不确定性对结构质量的影响要大得多.
参考文献
[1]GB 50011—2010建筑抗震设计规范[S]. 北京:中国建筑工业出版社,2010:33-35.
GB 50011—2010Code for seismic design of building[S]. Beijing: China Architecture & Building Press, 2010:33-35. (In Chinese)
[2]BEN-HAIM Y, ELISHAKOFF I. Convex models of uncertainty in applied mechanics [M]. Amsterdam: Elsevier, 1990:325-330.
[3]BEN-HAIM Y. Convex models of uncertainty: applications and implications[J]. Erkenntnis, 1994, 41(2): 139-156.
[4]MOENS D, VANDEPITTE D. A survey of non-probabilistic uncertainty treatment in finite element analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(12): 1527-1555.
[5]TAKEWAKI I, BEN-HAIM Y. Info-Gap robust design with load and model uncertainties[J]. Journal of Sound and Vibration, 2005, 288(3): 551-570.
[6]ELISHAKOFF I, ELISSEEFF P, GLEGG S A. Nonprobabilistic, convex-theoretic modeling of scatter in material properties[J]. AIAA Journal, 1994, 32(4): 843-849.
[7]BEN-HAIM Y. A non-probabilistic concept of reliability[J]. Structural Safety, 1994, 14(4):227-245.
[8]亢战,罗阳军. 基于凸模型的结构非概率可靠性优化[J]. 力学学报, 2006, 38(6): 807-815.
KANG Zhan, LUO Yang-jun. On structural optimization for non-probabilistic reliability based on convex models [J]. Acta Mechanica Sinica:Chinese Edition, 2006, 38(6): 807-815. (In Chinese)
[9]罗阳军,亢战. 超椭球模型下结构非概率可靠性指标的迭代算法[J]. 计算力学学报, 2009, 25(6): 747-752.
LUO Yang-jun, KANG Zhan. An iteration approach for structural non-probabilistic reliability analysis based on hyper-ellipsoidal models[J]. Chinese Journal of Computational Mechanics, 2009,25(6):747-752. (In Chinese)
[10]苏永华, 常伟涛, 赵明华. 深部巷道围岩稳定的区间非概率指标分析[J]. 湖南大学学报:自然科学版, 2007, 34(7): 17-21.
SU Yong-hua, CHANG Wei-tao, ZHAO Ming-hua. Non-probabilistic index analysis method of the stability of deep rock around roadway based on interval variable[J]. Journal of Hunan University:Natural Sciences, 2007, 34(7): 17-21. (In Chinese)
[11]BEN-HAIM Y. Info-Gap decision theory: decisions under severe uncertainty[M]. 2nd ed. London: Academic Press, 2006: 260.
[12]PIERCE S G, WORDEN K, MANSON G. A novel information-Gap technique to assess reliability of neural network-based damage detection[J]. Journal of Sound and Vibration, 2006, 293(1): 96-111.
[13]MOILANMEN A, WINTE B A. Uncertainty analysis favours selection of spatially aggregated reserve networks[J]. Biological Conservation, 2006, 129(3): 427-434.
[14]DUNCAN S J, BRAS B, PAREDIS C J. An approach to robust decision making under severe uncertainty in life cycle design[J]. International Journal of Sustainable Design, 2008, 1(1): 45-59.
[15]BEN-HAIM Y. Value-at-risk with info-Gap uncertainty[J]. Journal of Risk Finance, 2005, 6(5): 388-403.
[16]BEN-HAIM Y. Uncertainty, probability and information-Gaps[J]. Reliability Engineering & System Safety, 2004, 85(1): 249-266.
[17]RAO S S, BERKE L. Analysis of uncertain structural systems using interval analysis[J]. AIAA Journal, 1997, 35(4): 727-735.
[18]DAVIS L. Handbook of genetic algorithms[M].New York:Van Nostrand Reinhold, 1991: 325-330.
[19]刘思思,赵明华,杨明辉, 等. 基于自组织神经网络与遗传算法的边坡稳定性分析方法[J]. 湖南大学学报:自然科学版, 2008, 35 (12): 7-12.
LIU Si-si, ZHAO Ming-hua, YANG Ming-hui,et al. Slope stability analysis method based on self-organizing neural network and genetic algorithm[J]. Journal of Hunan University:Natural Sciences, 2008, 35(12): 7-12. (In Chinese)
[20]LEITE J P, TOPPING B H. Improved genetic operators for structural engineering optimization[J]. Advances in Engineering Software, 1998, 29(7): 529-562.
[21]AABEK O, DION C M, YEDDER A B H. Evolutionary algorithms for the optimal laser control of molecular orientation[J]. Journal of Physics B: Atomic, Molecular and Optical Physics, 2003, 36(23): 4667.
[22]BRAMLTTE M F, CUSIC R. A comparative evaluation of search methods applied to parametric design of aircraft[C]//Proceedings of 3th International Conference on Genetic Algorithms. Burlington,Massachusetts: Morgan Kaufmann Publishers Inc,1989: 213-218.
[23]吕西林,周定松. 考虑场地类别与设计分组的延性需求谱和弹塑性位移反应谱[J]. 地震工程与工程振动, 2004, 24(1): 39-48.
LV Xi-lin, ZHOU Ding-song. Ductility demand spectra and inelastic displacement spectra considering soil conditions and design characteristic periods[J]. Earthquake Engineering and Engineering Vibration, 2004, 24(1): 39-48. (In Chinese)

