柔性翻边成形工艺参数研究

尤舒曼， 李 杰， 赵亦希， 胡逸辉

(1. 上海交通大学 上海市复杂薄板结构数字化制造重点实验室，上海 200240；2. 首都航天机械有限公司，北京 100076)

多品种小批量的钣金结构件在航空领域应用广泛.目前，此类产品主要借助型胎并利用人工锤击法进行翻边成形[1].随着钣金结构件种类日益丰富，产品的开发周期逐渐缩短，而现有人工锤击翻边制造技术存在劳动强度大和成形效率低等局限，难以满足需求.此外，目前我国钣金成形技术正由传统的“设备粗成形+手工精校准”向“设备高效精确成形”转变[2].机器人柔性翻边成形工艺通过机器人引导滚轮，对薄板边缘进行多道次滚压使之形成翻边件，具有效率高和劳动强度低等特点，有望在钣金成形技术中得到推广应用.

多数航空钣金结构件的翻边长度值和高度值均较大，并且部分装配要求不允许在整条翻边上开工艺缺口，因此容易产生翻边缺陷.同时，机器人柔性翻边成形工艺是一种局部加载的连续成形工艺，成形时直接从平面薄板开始进行局部翻折，从而导致加载区与自由变形区之间、不同加载工步之间的强耦合和变形协调问题突出.此外，成形系统中的材料、滚轮、机器人和工艺路径等各环节对成形质量均有较大影响.对此，国内外学者通过仿真和试验研究以滚轮为成形工具的滚弯和滚压包边等工艺的成形质量问题，并重点关注滚轮形状尺寸、工作参数和毛坯尺寸等因素.研究结果表明：在滚弯成形时，道次数的增加可以减小回弹，有效提高成形质量[3-4]，但道次数过大会增加相邻道次之间互相影响的程度从而增加缺陷累积[5]；道次数与各道次翻折角度增量互相影响，单道次翻折角度增量的减小有利于滚弯中单道次边波的产生[5]；适当增加滚轮直径可以显著减小滚压板料所受应力[6]，但滚弯后的回弹半径也会相应增大[7].可知，道次数和滚压速度是影响成形效率的主要因素.而型材尺寸等因素在航空钣金件的翻边成形中可变范围较小，影响有限，不予考虑.因此，探索柔性翻边新工艺的变形规律，研究各种工艺参数对成形质量的影响是推广应用该工艺的重要突破口.

本文设计了外曲翻边缩比件，通过研究柔性翻边的三维有限元模型的建模方法，模拟特征件的翻边成形过程，分析其在局部加载下的翻边变形特点.探讨翻边道次数、各道次角度分配、滚轮直径和滚压速度等关键工艺参数对特征件成形质量的影响，优化工艺参数以提高翻边件的成形质量，建立柔性翻边试验系统并进行验证.

1 特征件的柔性翻边工艺

以常见航空薄壁钣金件为参考，设计带弧度的外曲翻边零件作为特征翻边件，其包括平面、过渡圆角和翻边共3部分，沿翻边线等距选取从左到右的5个测点A、D、B、E和C，如图1所示.特征翻边件的尺寸设计为翻边开角110°，翻边部分高25 mm、长224 mm，圆弧半径14 dm，过渡圆角半径3 mm，板厚2 mm.质量要求为翻边部分与模具之间的间隙，即贴模间隙d≤2.7 mm，且不允许开工艺缺口.

图1 特征翻边件示意图Fig.1 Diagram of a feature flanging part

机器人柔性翻边工艺的基本过程为将待成形薄板固定于胎模上，胎模的形状尺寸与目标零件一致.本文所研究的特征件，其翻边角度值和高度值均较大，一次翻折成形易硬化而发生断裂，且单道次的翻折角度过大会增大成形力，增加机器人负荷，因此翻边过程分为多道次进行(见图2).将成形过程按照恒定角度分为5个道次，每道次的进给角度，即翻边角度(翻边开角的补角)θ=14°，则依次为θ=14°，28°，42°，56°，70°.通过机器人示教，滚轮按照设置好的翻边路径轨迹，沿零件翻边线将薄板逐步弯曲，最终使得零件形成一定的翻边开角.

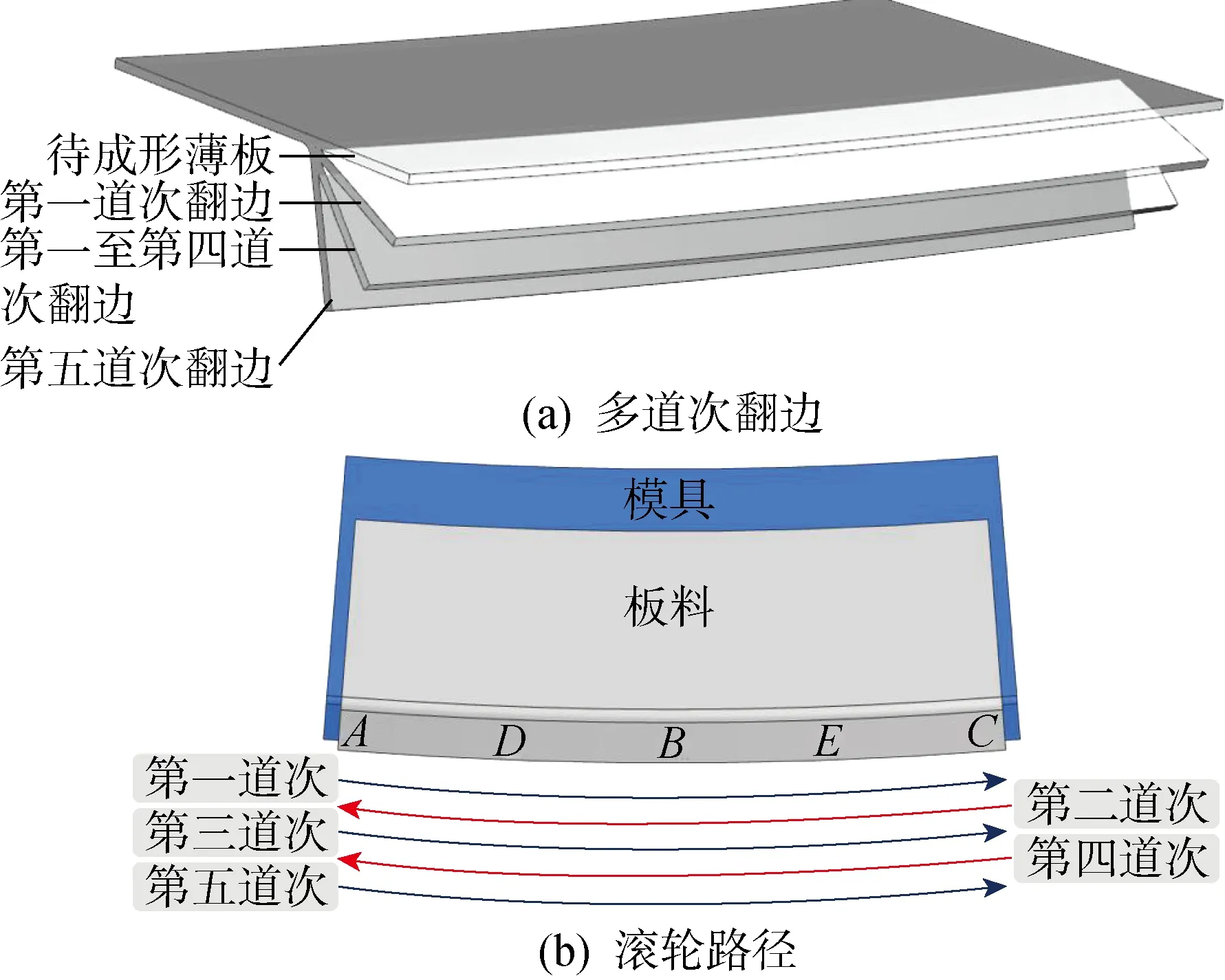
图2 多道次翻边路径示意图Fig.2 Rolling path of multi pass flanging

2 柔性翻边仿真

2.1 柔性翻边模型

选择Abaqus平台进行柔性翻边仿真分析.试验材料为5A06-O态铝合金，通过单拉试验得到材料的各基本参数为密度 2 640 kg/m3，弹性模量 70 GPa，屈服强度158.8 MPa，泊松比0.33.真应力-真应变(σT-εT)曲线如图3所示，通过拟合得到以下Hollomon方程：

图3 5A06-O态铝合金σT-εT及其拟合曲线Fig.3 σT-εT and fitting curves of 5A06-O aluminum alloy

有限元模型选用实体单元，厚度方向的网格数量设置为5个，尺寸为0.4 mm.同一块板料中不同区域的变形程度不同，因此将翻边件分为3个区域进行网格划分(见图4)：平面部分在滚压过程中不发生塑性变形，粗化网格尺寸，设置为(5～8) mm×1 mm；翻边部分因滚轮的局部连续加载而仅在周向和径向发生变形，网格尺寸设置为(2～3) mm×1 mm；过渡圆角部分被折弯而发生剧烈变形，应力情况较为复杂，为重点分析部分，需要细化网格尺寸，设置为1 mm×1 mm.

图4 板料不同区域的网格划分Fig.4 Grid division of sheet in different areas

柔性翻边仿真模型装配如图5所示，压板将板料固定在模具上.板料为可变形体，其他部件均为刚体.根据柔性制造的特点，选择圆柱型直滚轮[8]，滚轮直径l=50 mm，滚轮高度为34 mm(大于特征件的翻边高度).为提高仿真效率，减少相邻两道次之间滚轮因调整位姿角度而消耗的时间，将各道次不同倾角的滚轮导入仿真模型，当第一道次的滚压结束时，设置第一道次的滚轮与板料无接触，同时进行第二道次的滚轮与板料接触，并开始第二道次的滚压，依此类推.

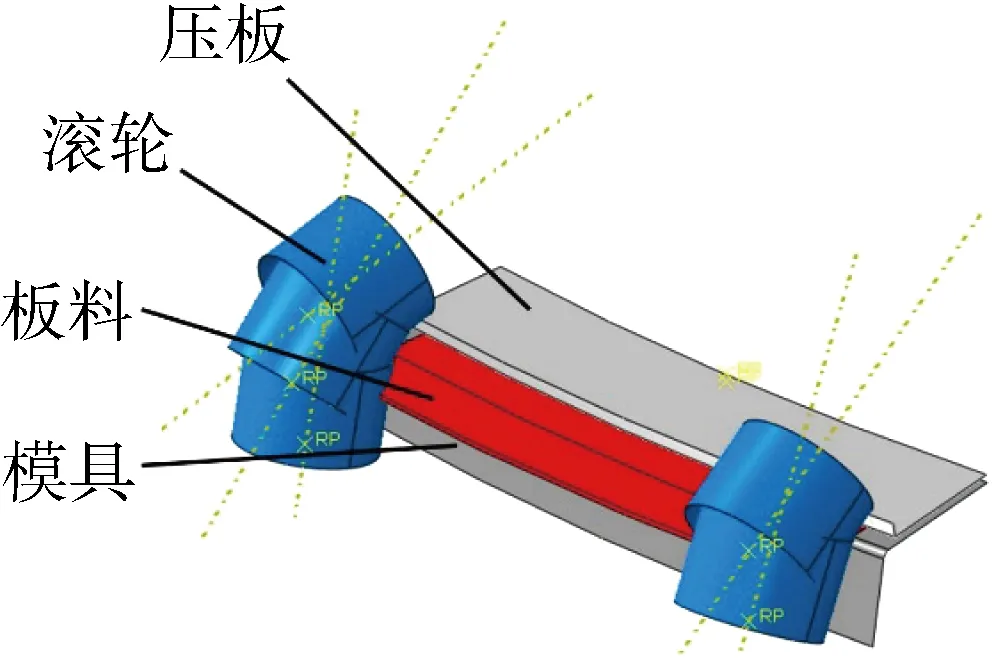
图5 仿真模型装配图Fig.5 Assembly diagram of simulation model

2.2 翻边成形过程模拟

滚轮的运动路径主要包括两种：① 切入运动，滚轮从初始状态逐步与板料接触，最终到达每道次滚压的起始位置；② 滚压运动，滚轮沿翻边线做周向的进给运动.滚压速度设置为v=50 mm/s.具体路径如图6所示.

图6 滚轮运动路径Fig.6 Motion path of roller

2.3 仿真结果分析

对根据上述设置得到的仿真建模参数和滚轮运动路径进行仿真分析，结果如图7所示.可知，特征翻边件无开裂和起皱等缺陷，表明柔性翻边能够完成特征翻边件的成形.过渡圆角处和翻边部分的平均板料厚度分别为1.999 mm和1.994 mm，板料厚度变化量分别小于3%和4%，即板料厚度变化可以忽略不计.

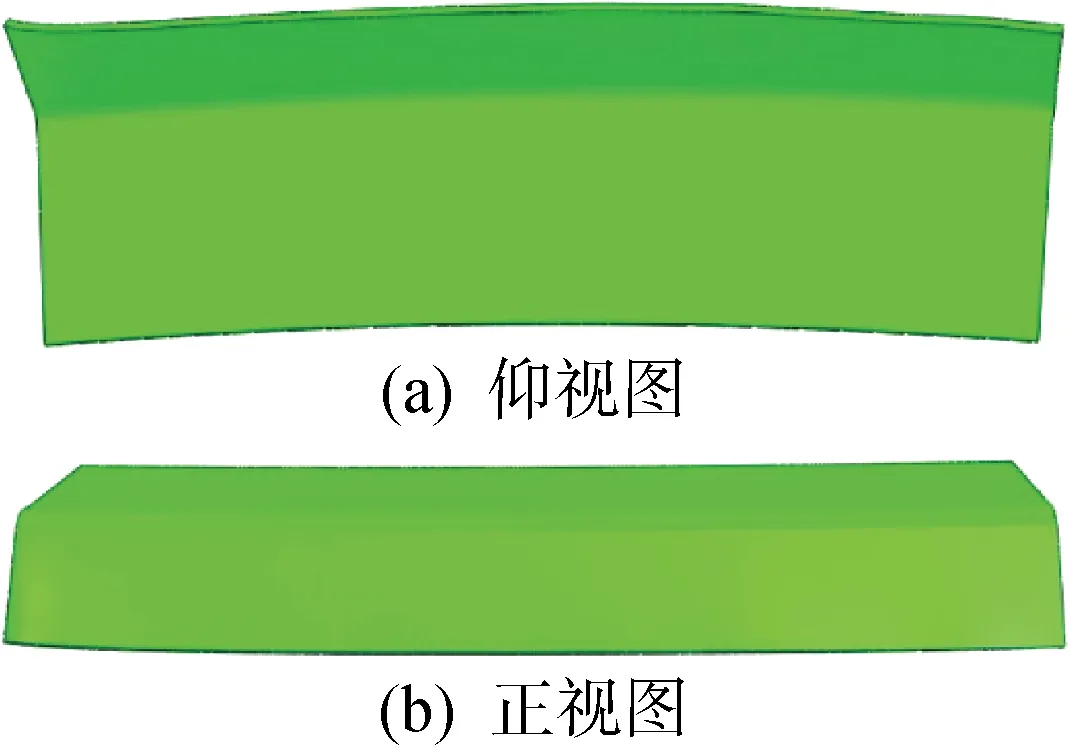
图7 仿真得到的特征翻边件Fig.7 Feature flanging part obtained by simulation

2.3.1应力应变分析 翻边完成后，翻边件上的等效塑性应变(PEEQ)分布如图8所示.过渡圆角处的等效塑性应变最大，翻边部分次之，平面部分最小(可忽略不计)，且左右两自由端的等效塑性应变相对较小.分析翻边件在点B横截面处的过渡圆角和翻边部分的等效塑性应变分布，发现等效塑性应变主要集中分布在板料内外表面 ，且在过渡圆角的外表面处取得最大值.

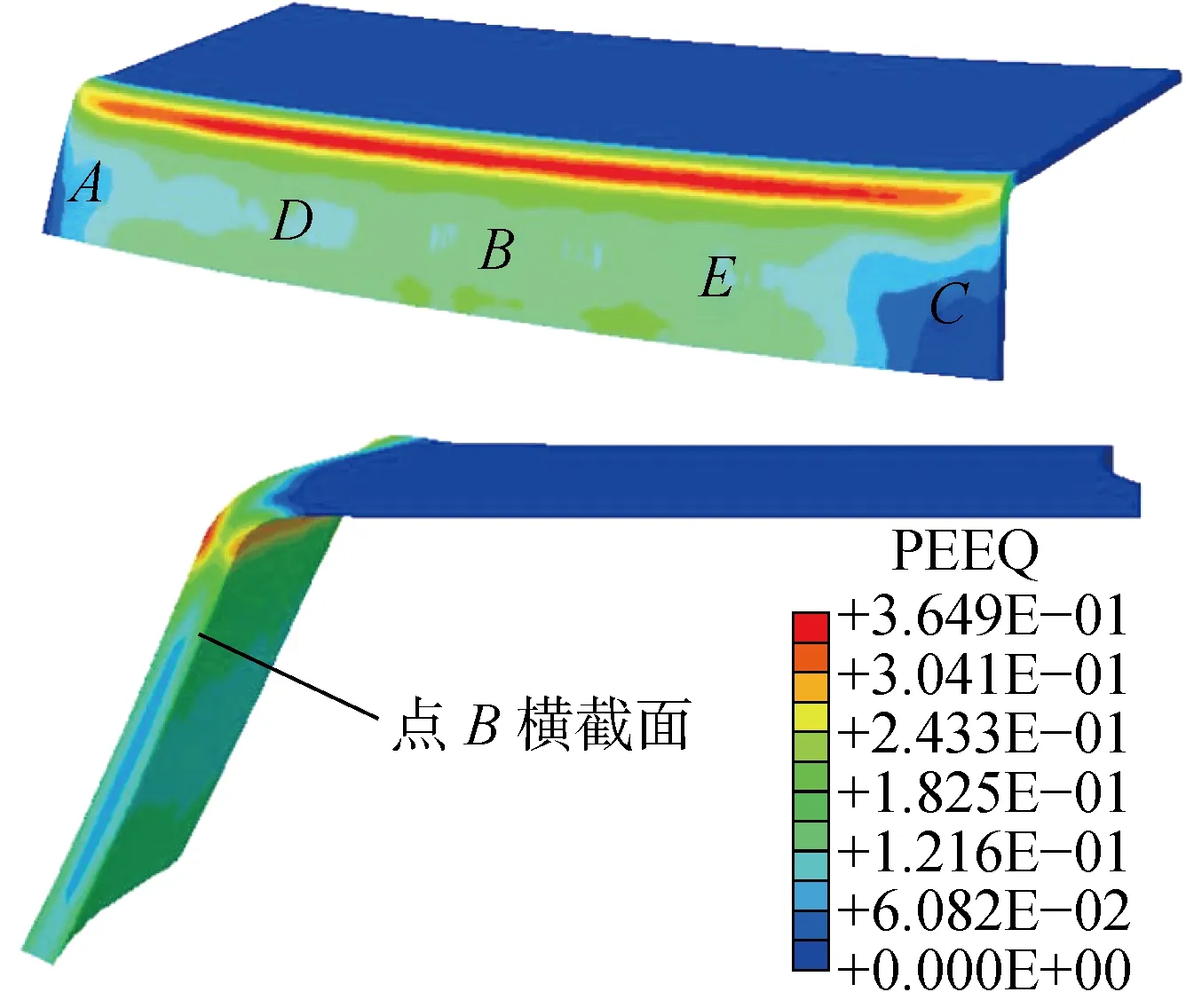
图8 翻边完成后的等效塑性应变分布云图Fig.8 Cloud diagram of equivalent plastic strain after flanging

翻边件在点B处各部分外表面的Mises应力(τ)变化曲线如图9所示.板料上的应力随滚压道次数的增加而逐渐增大，且过渡圆角处的应力值最大，翻边部分次之，平面部分最小(可忽略不计).

图9 各部分在B点处的Mises应力变化曲线Fig.9 Mises stress of each part at point B

翻边件的Mises应力分布云图(见图10)进一步验证了以上结论， 且发现板料上的应力主要集中分布在过渡圆角处，并在点A的过渡圆角处取得最大值403.8 MPa.此外，翻边件左右两自由端的应力分布不同：奇数道次滚压(滚压方向从左向右)结束后，翻边件在点A处的应力偏大，而偶数道次则相反.结合仿真模型的对称性分析可知，翻边完成后，翻边件两自由端的应力差异由最终道次的滚压方向决定.

图10 翻边件上的Mises应力分布云图Fig.10 Cloud chart of Mises stress distribution on flanging part

在滚压过程中，对最终道次翻边部分板料的变形特点进行分析，如图11所示.随着滚轮从左向右做滚压运动，板料在点A、D、B和E处的外表面应力状态变化为拉应力-压应力-拉应力，内表面则相反.而点C为滚压终点且为自由端，因此该处不受双边约束，最终应力状态与其他点不同：外表面应力状态变化为拉应力-压应力，内表面则相反.

图11 翻边件变形区应力状态Fig.11 Stress of flanging part in deformation zone

利用翻边件外边缘最大主应力(τmax)云图进行验证，结果如图12所示.当最终道次滚轮滚压至点B时，该点的内、外表面应力状态为压应力和拉应力.而滚压路径前后方各点的应力状态相反.综上可知，翻边件两自由端的应力状态差异由最终道次的滚压方向决定.

图12 翻边件外边缘的最大主应力分布云图Fig.12 Cloud chart of maximum principal stress distribution on outer edge of flanging part

2.3.2贴模间隙 贴模间隙是零件内表面与模具之间的贴合间隙，能够描述零件表面精度[9]，是考察航空钣金翻边件成形质量的重要指标.以点A为例计算特征件贴模间隙，如图13所示.

图13 翻边件的贴模间隙Fig.13 Die clearance of flanging part

提取翻边成形后点A处外边缘内表面的节点坐标xA、yA和zA，其中z表示高度方向.由于贴模间隙远小于翻边件的圆弧半径，所以翻边件外边缘可以近似为与胎模模面圆心相同的圆弧.胎模模面方程为

(1)

式中：R为圆弧半径.

计算点A和胎模上相同高度圆弧上的任意点A*(zA*=zA)到圆心的距离：

(2)

(3)

点A*与圆心在同一条水平直线上，因此两点之间的水平距离

Δx=rA-rA*

贴模间隙与水平距离的关系如图14所示，可表示为

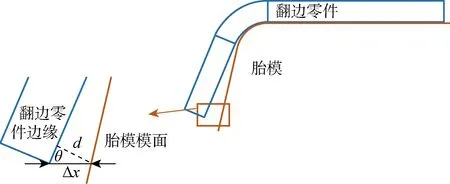
图14 贴模间隙的计算示意图Fig.14 Calculation of die clearance

d=Δxsinθ

将式(2)和(3)代入，得到贴模间隙的计算公式：

根据上述方法，得到所有待测点的贴模间隙，并形成特征件的贴模间隙曲线，如图15所示.其中，点A、D和B处的贴模间隙以及整体的贴模平均值(2.77 mm)均超过翻边零件质量要求的2.7 mm，且波动范围(极差)高达1.19 mm，不满足质量要求.因此，需要进一步减小翻边贴模间隙，提高贴模间隙一致性，以优化成形质量.

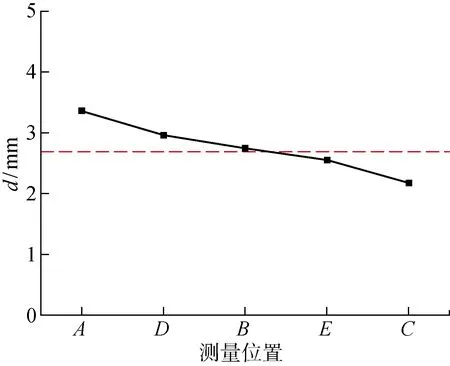
图15 翻边特征件的仿真贴模间隙分布Fig.15 Simulation of die clearance distribution on feature part

3 工艺参数对翻边成形质量的影响

3.1 正交试验设计

利用正交试验对各因素各水平进行试验方案设计，并综合分析试验结果，探究各因素水平的最佳组合，得到最优或较优的试验方案.

对影响柔性翻边成形质量的翻边道次数、各道次角度分配、滚轮直径和滚压速度共4个因素进行研究.各因素取3个水平进行设计，具体取值如表3所示.各道次角度分配方案因翻边道次数不同而有所区别，因此仅以逐渐增大、逐渐减小和保持不变区分.例如，当翻边道次数为7时，若各道次角度分配保持不变，则有θ=10°，20°，30°，40°，50°，60°，70°，即每道次的进给角度为10°.

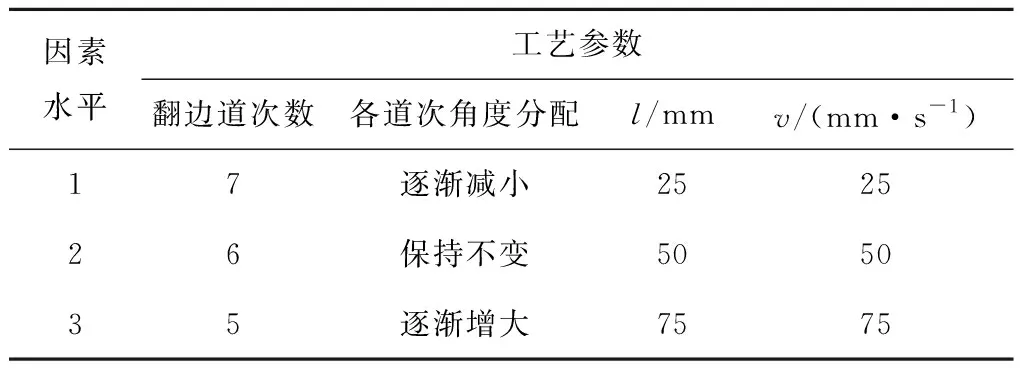
表3 各因素水平取值Tab.3 Selected values of factors

柔性翻边工艺参数设计的正交表为L9(34)，即正交试验为4因素3水平，共9组试验，具体设计如表4所示.

表4 柔性翻边工艺参数研究正交试验设计Tab.4 Orthogonal text design of flexible flanging process

对上述正交试验设计的试验条件进行仿真分析，处理结果如表5所示.

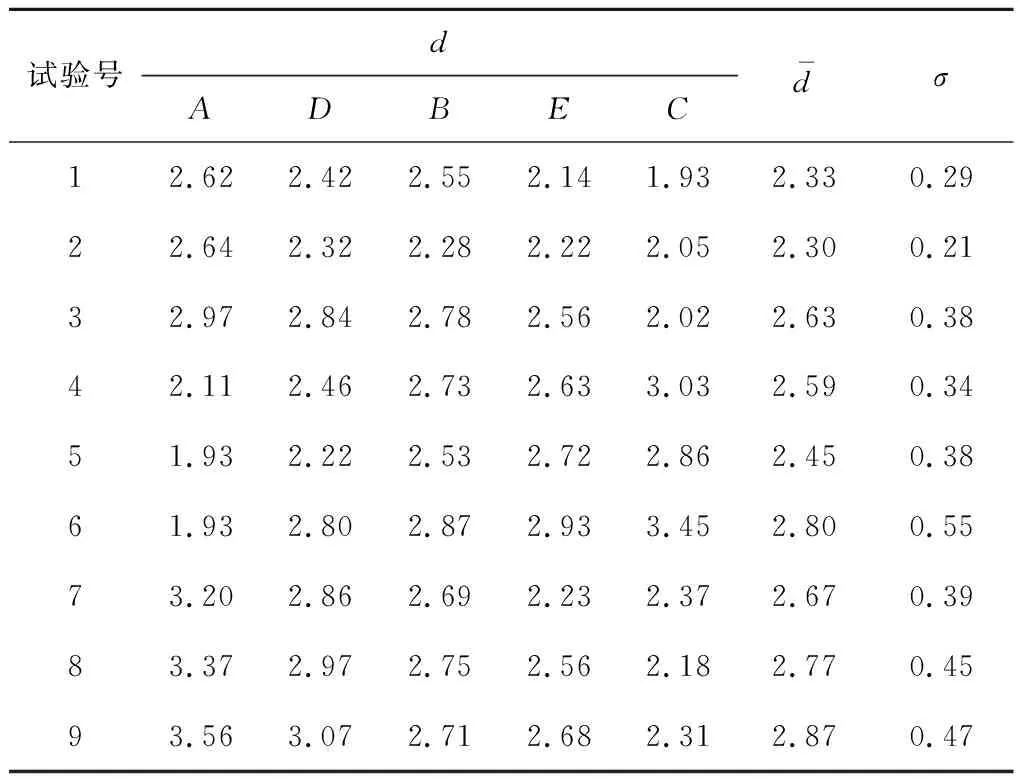
表5 各试验条件仿真的贴模间隙

3.2 工艺参数对贴模间隙的影响

根据上述仿真数据计算贴模间隙平均值，利用极差分析法进一步分析数据，结果见表6.根据极差大小，可以比较各工艺参数指标对贴模间隙平均值影响的敏感性：翻边道次数最大，各道次角度分配次之，滚压速度再次之，滚轮直径最小(可忽略不计).

表6 正交试验计算贴模间隙平均值Tab.6 Average value of die clearance by orthogonal test

敏感性较强的3个指标与贴模间隙平均值之间的关系如图16所示.可知， 当翻边道次数越大或滚压速度越小时，贴模间隙平均值越小；而当各道次角度分配保持不变时，贴模间隙平均值最小.

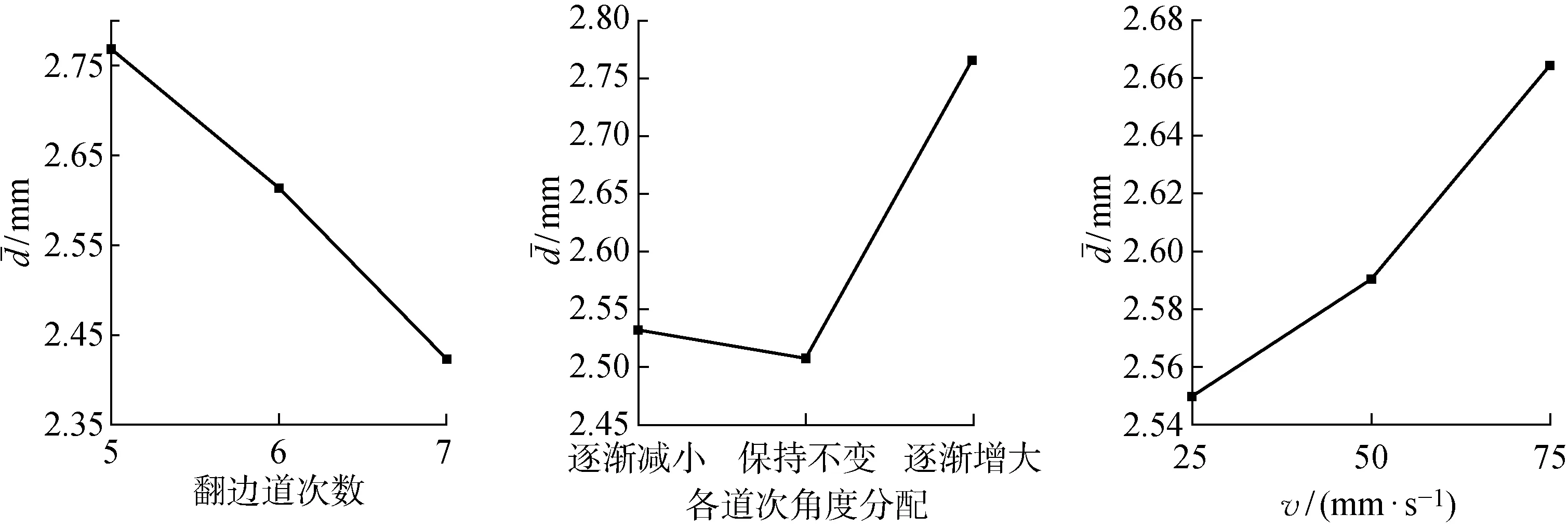
图16 各工艺参数指标对贴模间隙平均值的影响Fig.16 Average value of die clearance versus different process parameters

3.3 工艺参数对贴模间隙一致性的影响

利用极差分析法对贴模间隙标准差进行分析，结果如表7所示.根据极差大小，可以比较各工艺参数指标对贴模间隙标准差影响的敏感性：翻边道次数最大，各道次角度分配次之，滚轮直径再次之，滚压速度最小(可忽略不计).

表7 正交试验计算贴模间隙标准差

敏感性较强的3个指标与贴模间隙标准差间的关系见图17.可知，翻边道次数越大，贴模间隙标准差越小，一致性越好；而当各道次角度分配逐渐减小或l=50 mm时，贴模间隙标准差最小，一致性最好.

图17 各工艺参数指标对贴模间隙标准差的影响Fig.17 Standard deviation of die clearance versus different process parameters

3.4 工艺参数优化设计

综合分析正交试验设计的仿真结果，得到各工艺参数对成形质量的影响如下：

(1) 翻边道次数对翻边成形质量的影响最显著.随翻边道次数增加，翻边件的贴模间隙减小且一致性变好，成形质量得到改善.

(2) 各道次角度分配对翻边成形质量的影响较显著.当各道次角度分配保持不变时，翻边件整体贴模情况最好；当其逐渐减小时，贴模间隙一致性最好.且其保持不变与逐渐减小时的贴模间隙一致性差异较小(见图18).因此，当各道次角度分配保持不变时更有利于改善成形质量.

(3) 滚轮直径和滚压速度对翻边成形质量的影响较小.当l=50 mm时，贴模间隙一致性较好；滚压速度越小，则整体贴模情况越好.但是，当v=25 mm/s 和v=50 mm/s时，整体贴模情况相差很小，而成形效率相差较大(约1倍)，因此选择v=50 mm/s.

综合考虑翻边件的整体贴模情况、不同位置的贴模间隙一致性和成形效率等因素，得到本特征件工艺参数的最优组合：7道次、各道次角度分配保持不变、l=50 mm和v=25 mm/s.并与5道次、各道次角度分配逐渐增大、l=50 mm和v=25 mm/s的仿真贴模数据进行比较，结果如图18所示.可知，经工艺参数优化设计后，贴模间隙平均值减小了19.9%，满足了翻边零件质量要求；贴模间隙平均值的波动范围减小了52.8%，贴模间隙一致性得到改善.

图18 工艺参数优化结果Fig.18 Optimization results of process parameters

4 机器人柔性翻边试验验证

4.1 试验系统搭建

搭建包括机器人、工作台支架、模具、滚轮和滚轮支座等的机器人柔性翻边试验系统，如图19所示.利用工业六轴机器人控制直径为50 mm的圆柱直滚轮对板料进行翻边成形.将待成形薄板放置在工作台支架上，根据模具上的3个限位销钉进行定位，并利用压板和肘夹对翻边件的平面部分施加压边力使得板料固定在模具上.

图19 机器人柔性翻边试验系统Fig.19 Test system of robot flexible flanging

同图1所示在翻边试验件上等距离选择5个测点，并利用塞尺测量翻边件翻边部分的贴模间隙，如图20所示.

图20 贴模间隙测量量规Fig.20 Gauge for measuring die clearance

4.2 试验结果分析

在7道次、各道次角度分配逐渐减小、l=25 mm 和v=25 mm/s的条件下，对比试验与仿真结果.可知，翻边试验件无开裂和起皱等缺陷(见图20)，同仿真结果一致.在成形前，板料厚度平均值为2.014 mm；在成形后，试验件的过渡圆角和翻边部分处的板料厚度平均值分别为2.086 mm和 2.022 mm，即板料厚度变化小于5%.

翻边件贴模间隙的试验和仿真数据如表8所示，对比曲线如图21所示.可知，试验件同样存在贴模间隙较大且一致性较差的问题；除了点B处的试验与仿真数据偏差略大于0.10，其余各点处的偏差均小于0.10；随着测量点位置的变化，试验和仿真中贴模间隙的变化趋势相同，即翻边件在点A处的贴模间隙最大.

表8 试验与仿真的贴模间隙Tab.8 Die clearance of text and simulation

图21 试验与仿真贴模间隙对比曲线Fig.21 Die clearance curves of text and simulation

综上可知：仿真计算结果在允许误差范围内，仿真模型的有效性得到验证，4个工艺参数对翻边件成形质量影响规律的研究结果具有较高的可信度.

5 结论

机器人柔性翻边新工艺具有生产柔性强的特点，适用于多品种、小批量航空钣金结构件的翻边成形，是一种精确高效的成形方法.利用仿真和试验进行该方法的工艺规律研究，经仿真得到优化的工艺参数，并进行试验验证，得到符合要求的翻边成形件.主要结论如下：

(1) 机器人柔性翻边成形工艺能够完成航空钣金翻边件的成形，且翻边件无开裂和起皱等缺陷.

(2) 翻边件的应力主要集中在过渡圆角处，且最终道次的滚压方向决定了翻边件左右两端的应力差异；成形质量缺陷主要由翻边部分的贴模间隙未达到设计要求造成.

(3) 翻边道次数对成形质量的影响最大，各道次角度分配次之，滚轮直径或滚压速度最小.

(4) 在对不同翻边件进行工艺参数设计时，建议尽可能增加道次数以提高成形质量，并令各道次角度分配保持不变；适当增大滚压速度以提高成形效率；在无空间限制的情况下，优先选择大直径滚轮以增大翻边件的贴模间隙一致性.

在后续研究中，将进一步对各工艺参数之间的耦合关系展开研究，并对材料和工艺路径等对翻边成形质量的影响进行讨论，以得到更全面的规划方案.