超高速磁浮轨道梁体系的跨平台耦合振动分析

蔡文涛， 王春江， 滕念管， 文 泉

(上海交通大学 船舶海洋与建筑工程学院， 上海 200240)

近年来，我国在高速铁路建设方面取得了突飞猛进的发展，并彻底改变了人们的出行方式，大大促进了我国社会和经济的发展.轮轨式高速铁路依靠轮轨之间的黏着力获得驱动力，黏着力随着速度的增加而快速减小，因此，轮轨式列车很难实现超过400 km/h的运营速度.相较于传统的轮轨列车来说，磁浮列车的优势在于与轨道进行非接触式运行，线路损耗小，速度快，噪声小.除此之外，磁浮列车的爬坡能力强，转弯半径也小，更适用于狭窄的地域.2002年12月建成通车的上海龙阳路-浦东机场的磁浮运营试验线采用了德国的TR型常导高速磁浮系统，最高运营时速达到了430 km，经过十多年的示范运营，效果良好.随着我国经济和社会的快速发展，我国科技部于2017年适时启动了时速600 km以上超高速磁浮轨道技术的研发项目.超高速磁浮系统主要由线路、车辆、供电及磁浮控制系统4个主要部分组成.与超高速磁浮系统相匹配的轨道梁体系在结构振动响应方面比一般的高速磁浮系统有更高更苛刻的要求，因此必须研制与之相匹配的轨道体系结构.基于此目标，研究超高速条件下磁浮列车-轨导梁体系的耦合动力学模型和分析方法是非常关键的，这也是对超高速磁浮线路在各种复杂形势的路线和工况条件下进行安全和舒适性分析的基础.本文在耦合系统的搭建方面进行了有意义的探索和实践，基于Simpack、ANSYS及Simulink这3个软件搭建了跨平台的耦合分析软件系统，并针对超高速磁浮系统进行了初步的参数分析，讨论了3节编组磁浮列车在不同速度、有无桥墩的情况下对磁浮-轨道梁体系竖向耦合系统的动态性能和影响规律，从而为超高速磁浮线路和车桥耦合响应等的关键参数研究提供技术参考.

1 磁浮列车-桥耦合分析现状

国内外学者对磁浮-轨道梁耦合振动做了大量的研究.鲍佳等[1]提出基于加速度-速度-位置的状态反馈，并在多刚体动力学软件中通过仿真验证了控制方法的可行性.滕延锋[2]基于PD控制(比例-微分)建立了10自由度车辆模型并对磁浮上海线已有梁型进行了振动分析，并与现场实测进行对比.Talukda等[3-4]在Simulink框架下搭建了磁浮-轨道梁模型，将车辆理想化为一系列的运动力，车体简化为二系弹簧阻尼系统，并借助Simulink框架对磁浮列车通过两跨连续梁进行了舒适度研究分析.文献[5]对中低速磁浮列车和大跨度连续梁进行了仿真模拟，对中低速磁浮的舒适度进行了分析计算.文献[6]将5模块中低速磁浮列车按照实际布置简化为离散的质量块，分析了两种典型轨道梁与中低速磁浮列车的耦合动力特性.文献[7]采用有限元法建立导轨梁，并用实测数据对其进行了修正，将车体模拟成为一个10自由度的模型，以上海高速磁浮商业运营线和同济大学高速磁浮试验线为例，对模型进行了验证.文献[8]基于UM多体软件建立了磁浮列车和轨道梁的耦合模型，并验证了程序的可行性.以上研究对磁浮列车-轨道梁耦合振动进行了诸多细致的分析，也得出了很多具有工程实际意义的结论.

当磁浮列车速度达到600 km/h以上时，原有的研究模型和轨道梁参数就需要做出调整，特别是针对超高速运行工况下的磁浮-轨道梁体系的耦合动力响应特征和规律，需要进行更细致的研究.目前国内外大部分有关磁浮的研究中对于超高速磁浮的研究较少，也没有考虑到桥梁桥墩的参振对超高速磁浮列车-桥耦合的影响，为研究此类运行工况下超高速磁浮-轨道梁体系的动力响应，并评估控制系统的动态性能，本文基于多体动力学软件Simpack建立了磁浮列车-控制器-轨道梁的耦合振动分析系统，将整个系统划分为车辆主系统、控制器子系统、轨道梁及桥墩子系统.其中，三维梁柱单元采用大型有限元软件ANSYS的BEAM188，磁浮控制模块采用MATLAB/Simulink，实现了PID控制器对整个磁浮控制系统进行主动控制.

2 磁浮列车模型

本文车辆模型采用上海线磁浮列车的模型参数[9].磁浮列车的动力学模型采用6自由度空间刚体模型，每列车通过弹簧与阻尼器与4个具有6自由度空间刚性体的转向架连接，磁浮列车-轨道桥系统如图1所示，各模块的动力自由度数如表1所示.

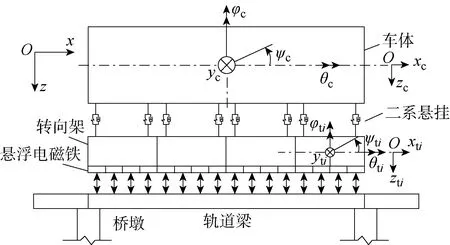
图1 磁浮系统模型Fig.1 Model of maglev system

表1 磁浮列车动力学模型自由度Tab.1 Degrees of freedom of dynamic model of maglev train

磁浮列车转向架由前后2个C型框、左右悬浮电磁铁及导向电磁铁等级部分构成，车厢和转向架间用空气弹簧连接，转向架的三维构造示意图如图2所示.

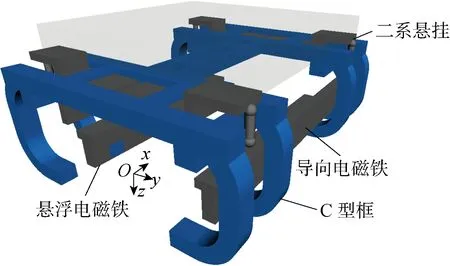
图2 转向架示意图Fig.2 Diagram of bogie

磁浮列车-轨道桥耦合系统中，车体、转向架、轨道梁的动力方程分列为

(3)

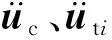
3 磁浮控制器原理和实现

3.1 电磁铁模型

电磁铁系统包括安装在轨道梁上的定子、铁芯、恒流线圈、控制线圈以及电磁回路.当忽略绕组漏磁通，并忽略铁芯和导轨中的磁阻时，根据安培环流定律，磁间隙处的磁场强度Bm为

(4)

式中：μ0为空气磁导率；c为磁间隙大小；Nconst为恒流线圈匝数；Iconst为恒流源电流；Nc为控制线圈匝数；Ic为控制电流.

磁场在磁间隙处产生的电磁吸引力f为

(5)

式中：Am为磁极面积.将式(4)代入式(5)得电磁力的表达式为

(6)

3.2 控制器原理

磁浮列车的悬浮系统是先天开环不稳定的系统，要实现磁浮列车的稳定悬浮，必须加控制系统进行闭环的反馈控制，闭环控制能够依靠反馈环节进行调节，一旦磁浮间隙过大，线圈电流随之增大，悬浮电磁力进而增强以抑制磁浮间隙的增加；反之磁浮间隙过小，线圈电流变小，从而抑制间隙的减小.PID控制器是目前较为主流的控制方法，它将磁浮间隙偏差的比例(P)、积分(I)及微分(D)进行线性组合成为控制量，并对磁浮间隙进行控制，其数学方程可表示为

(7)

式中：U(t)为电压随时间变化的函数；t为时间；Kpu为比例常数；e(t)为磁浮间隙随时间变化的函数；Ti为时间积分常数；Td为微分常数.

基于加速度、速度及位移的控制器进行反馈调节，控制电流可以表示为1个关于磁浮间隙的二阶微分方程[1]：

ΔI(t)=KpΔc(t)+KvΔv(t)+KaΔa(t)

(8)

式中：Kp、Kv及Ka分别为位移、速度以及加速度的反馈系数；Δc(t)、v(t)及a(t)分别为磁浮间隙增量、速度增量以及加速度增量.系统流程如图3所示，图中：T1a、Th及T2为滤波器时间常数；ω0、ξ0为观测器特征频率和阻尼；c0为额定的磁浮间隙；s表示拉氏变换；ξ0为观测器的阻尼；kf为电磁力比例系数.将测得的电磁铁与轨道面的加速度a输入至带通滤波器，将Δc输入低通滤波器，通过状态观测器将所测得的间隙信号和加速度信号进行重构来获取速度信号.然后把Δc、a以及重构的速度状态量与Ka、Kv以及Kp相乘得到电流变化量ΔI，与平衡位置的额定电流I0相加得到总的电磁铁电流，最后由控制器产生电磁吸力F.

图3 控制器流程Fig.3 Flowchart of controller

4 轨道梁有限元模型

4.1 梁单元模型

轨道梁模型采用Timoshenko梁单元，相较于Euler-Bernoulli的梁模型，Timoshenko梁单元模型只假定梁变形前垂直梁轴线的横截面，变形后仍为平面(刚性截面假定)，引入了剪切变形的影响.

对于本文所研究对象，采用有限元软件ANSYS中的Beam188单元进行模拟，Beam188单元是考虑横向剪切变形和截面转动惯量影响的Timoshenko梁单元.该单元是三维的双节点单元.Beam188单元在每个节点上有7个自由度，包括x，y，z方向的平动、围绕x，y，z方向的转动和截面翘曲自由度.

4.2 轨道梁体系截面参数

为了研究磁浮列车在桥梁上运动时的系统动力特性，磁浮轨道梁采用与时速600 km/h配套的24.768 m的简支梁为原型[10]，轨道布置为单线形式，轨道梁和墩型截面如图4所示, 参数见表2.

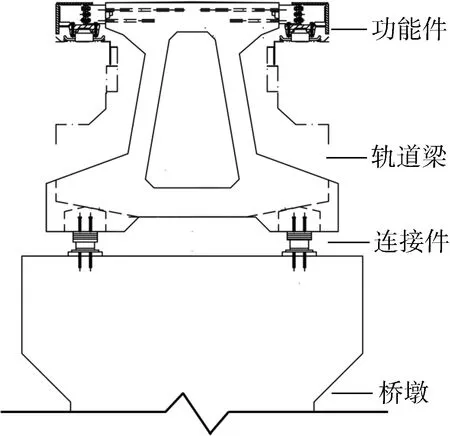
图4 轨道梁和桥墩截面Fig.4 Cross-section of track beam and pier

表2 轨道梁和桥墩参数Tab.2 Parameters of track beam and pier

注：表中Eb为轨道梁的弹性模量；Iy和Iz为轨道梁沿坐标轴方向的惯性矩.

采用Beam188单元对上述模型有限元化，为了保证模拟磁浮作用力的连续性，单元划分尺寸取为单个电磁铁长度的1/8.针对考虑桥墩参振的轨道梁和不考虑桥墩参振的轨道梁分别进行模态分析，分析结果如表3所示.

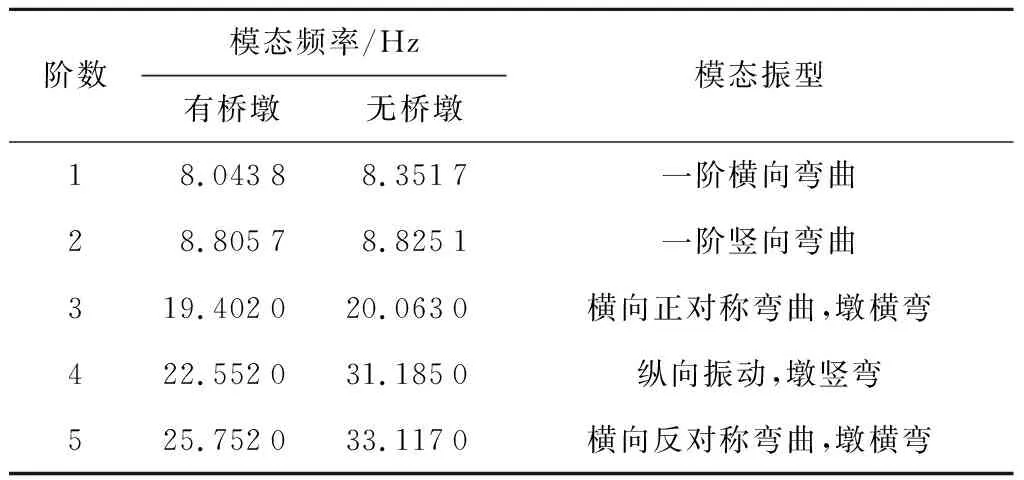
表3 模态分析结果Tab.3 Results of modal analysis

5 跨平台车桥耦合方法的实现

整个磁浮列车-轨道耦合系统由列车子系统、轨道梁-桥墩子系统和悬浮控制子系统3个部分组成，轨道梁和悬浮控制子系统分别作为耦合系统模型的子模型在不同的软件平台上建立.

通过ANSYS将轨道梁模型的模态分析结果以子结构形式输出到3个文件，分别为超单元矩阵信息文件(*.sub)、几何信息文件(*.cdb)以及应力信息文件(*.tcms)，这3个文件通过Simpack自带的柔性体模块生成可供多体动力学分析程序识别的模态信息文件(*.fbi)，实现ANSYS和Simpack之间的模型信息转换.

Simpack中可实现的控制器子模型主要有3种建立方法[11]：① Simpack自带的控制模块，通过对Simpack本身自带的控制模块进行参数设置和控制子系统的建模；② 通过MATLAB的SIMAT接口，与Simpack实现实时的控制数据的交互；③ 利用在MATLAB中的MATSIM模块，通过把设计好的控制器导出到动态链接库文件文件(*.DLL)，将该控制程序输入到Simpack的控制模块来实现控制系统的应用.从计算效率和便捷性方面综合考虑，本文采用了第3种控制器建模方法.

整个磁浮列车-轨道桥耦合系统分析功能的具体实现流程如图5所示.

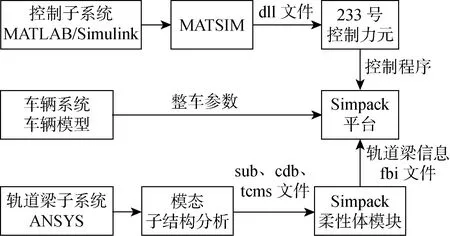
图5 模型仿真流程图Fig.5 Flowchart of model simulation

6 车桥耦合系统的动力响应

6.1 模型参数设置

本节采用上述仿真分析框架模拟了3节编组磁浮列车通过6跨简支梁的动力响应，具体数据参照文献[9]中磁浮列车的参数，额定磁浮间隙设定为10 mm，具体的磁浮列车参数如表4所示.

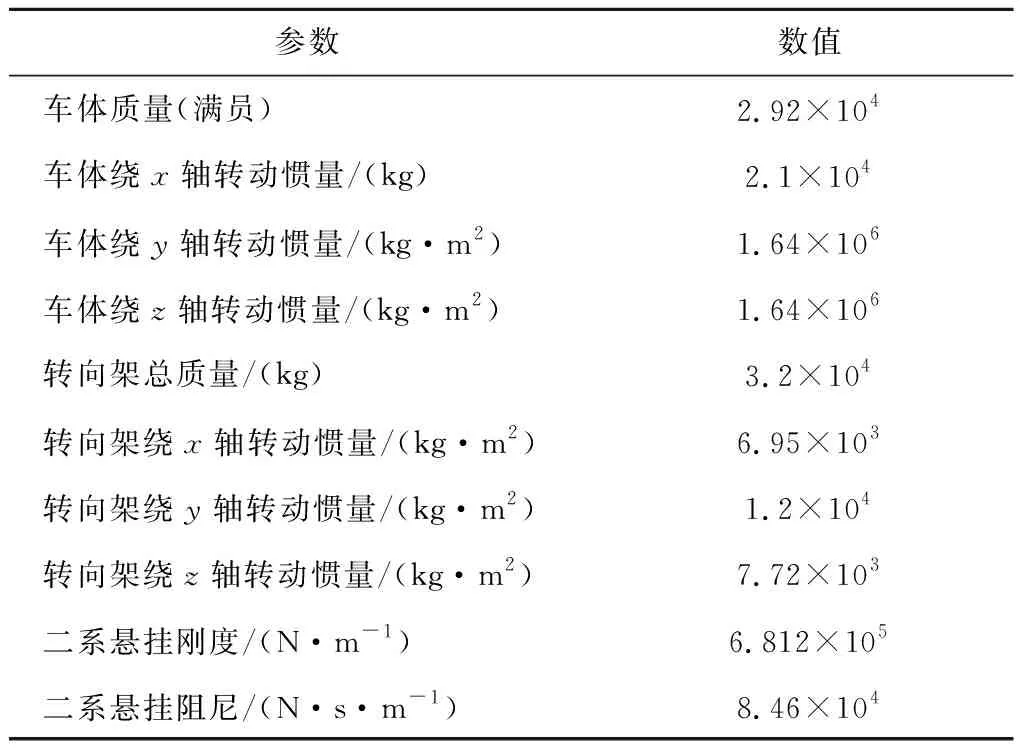
表4 磁浮列车参数Tab.4 Parameters of maglev train

轨道梁为预应力混凝土梁，轨道梁截面形式如图4所示.仿真时分析采用了不同磁浮列车时速工况下进行动力耦合计算，为精细模拟超高速列车的动力时程响应过程，仿真输出采样频率取500 Hz；仿真积分类数值分析方法采用SODASRT-2积分方法，该积分方法计算效率高，并可进行刚性模型和柔性模型代数微分方程(OAE)和常微分方程(ODE)的动力计算，该算法允许通过最大步长控制，算法稳定性高，适用于超高速车-轨道桥耦合系统的动力响应分析计算.

6.2 模型验证

为了验证提出的磁浮列车-轨道桥耦合机理分析方法的正确性以及模型的可靠性，将本文耦合模型所得的仿真结果与上海线在车速为300 km/h时的测试数据进行了对比[2]，结果如图6所示，图中：yb为轨道梁跨中竖向位移.

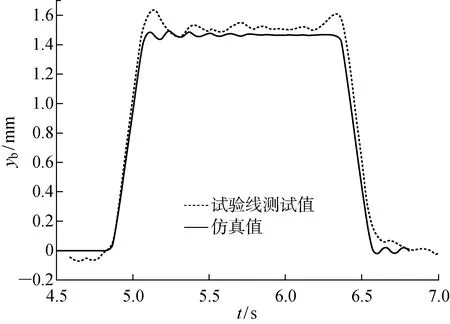
图6 实测结果与仿真结果对比Fig.6 Measured results versus simulation results

从图6可看出，仿真计算的分析结果与实测结果较为吻合，在300 km/h的车速下跨中竖向位移的理论值和实测值相差很小，最大为0.2 mm.通过比较磁浮列车上桥、桥面行进及下桥3个过程的数据发现，仿真数据与实测数据相比较，在车头抵达右支座和在车尾刚刚开始离开轨道梁时的起伏和偏差都稍大，这与轨道梁的刚度分布规律和变形转角变化规律是一致的.基于上述的模型比较验证，可以认为本文提出的磁浮列车-轨道桥耦合模型的计算分析方法和计算平台是可靠的，具体的时间积分步长根据不同的车速做适当调整，满足数值计算的精度和收敛性的要求.

6.3 桥梁动力响应分析

在磁浮列车时速达到600 km/h时，轨道梁跨中竖向位移时程曲线模拟结果如图7所示.取第1、3、6跨的跨中竖向位移进行跟踪分析，三跨的轨道梁变形规律基本一致，轨道梁竖向位移最大值为1.48 mm，磁浮轨道梁竖向动位移一般要求是不超过设计磁浮间隙±2 mm限值.

图7 轨道梁跨中竖向位移时程曲线Fig.7 Vertical displacement-time history curves at mid-span point

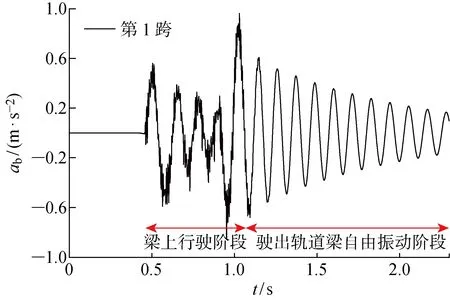
图8 轨道梁跨中竖向加速度时程曲线Fig.8 Vertical acceleration-time history curves at mid-span point

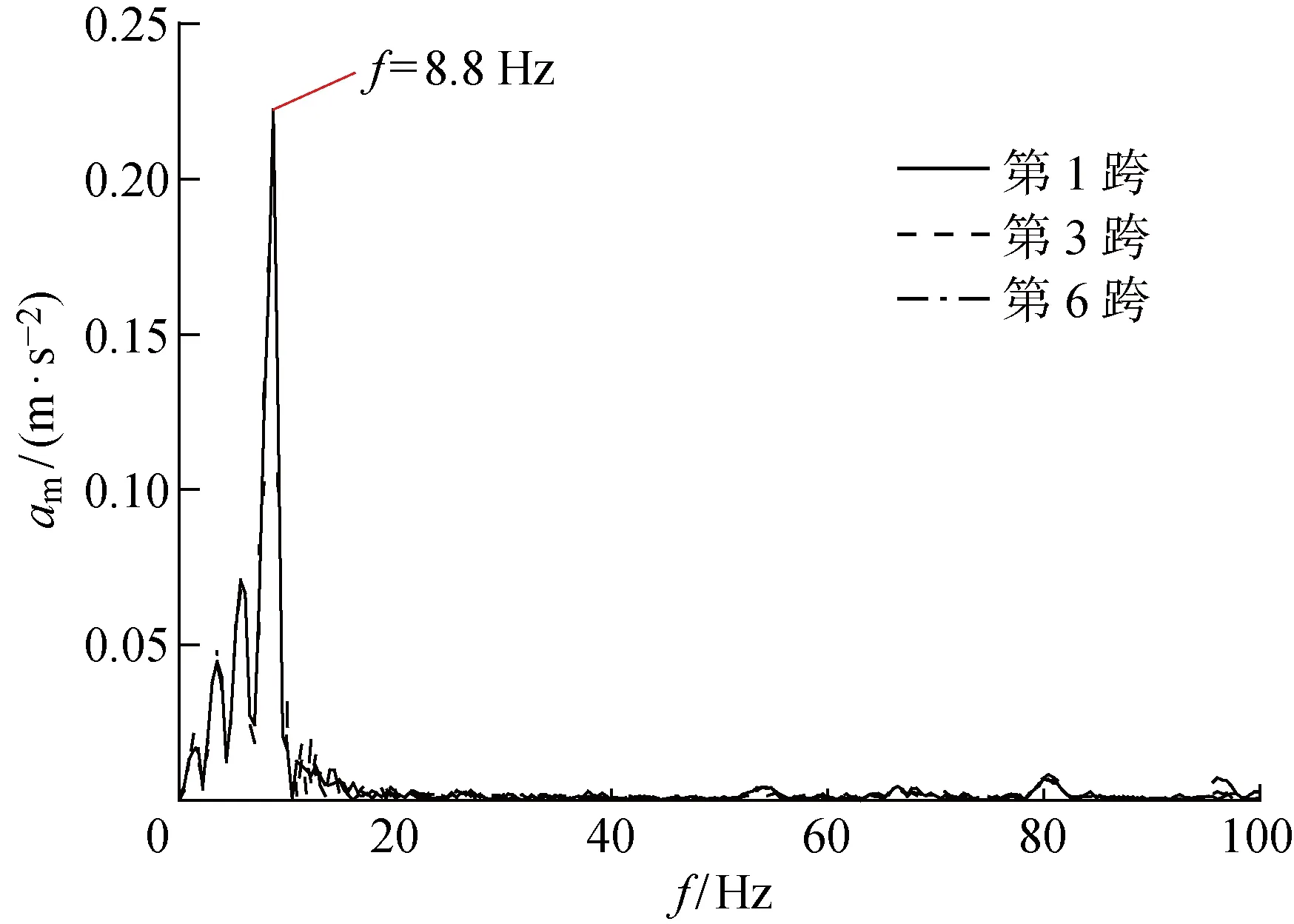
图9 轨道梁跨中竖向加速度频谱Fig.9 Vertical acceleration spectrum at mid-span point

第1跨桥梁跨中竖向加速度时程曲线(ab-t)以及第1、3、6跨相应的加速度频谱图(am-f)分别如图8、9所示.通过结果分析发现，轨道梁跨中加速度最大值约为1 m/s2，并且发生在磁浮列车入桥和出桥的时间点.通过分析第1、3、6跨相应的三跨桥加速度频谱，这3条曲线基本一致，且都有一个8.8 Hz对应的频谱峰值.结合之前对梁的模态分析结果(表3)，该值接近于梁的一阶竖向基频.对于连续简支桥梁而言，一阶竖向弯曲模态对桥梁的振动贡献最大.

6.4 车体动力响应分析

在磁浮列车-轨道桥耦合分析过程中，取车体几何中心点、悬浮架中心点及第1节电磁铁中心3个观测点，用于监测车辆系统的动力响应.图10所示为电磁铁磁浮间隙的时程曲线(d-t图)，图中悬浮间隙随着跨数的增加进行有规律的波动，波动区间的最大值为10.05 mm，最小值为9.90 mm，满足磁浮列车对于额定间隙在8～12 mm间悬浮控制要求.通过对比图7和10，结合位移时程曲线可以看出，电磁铁运动在经过轨道梁的交界处时，悬浮间隙会产生一定程度的突变，在轨道梁跨中位置又会出现一定程度的小的平台段，这与磁浮力的变化规律是一致的，也反映了轨道梁的刚度沿着跨度方向的梯度变化规律.

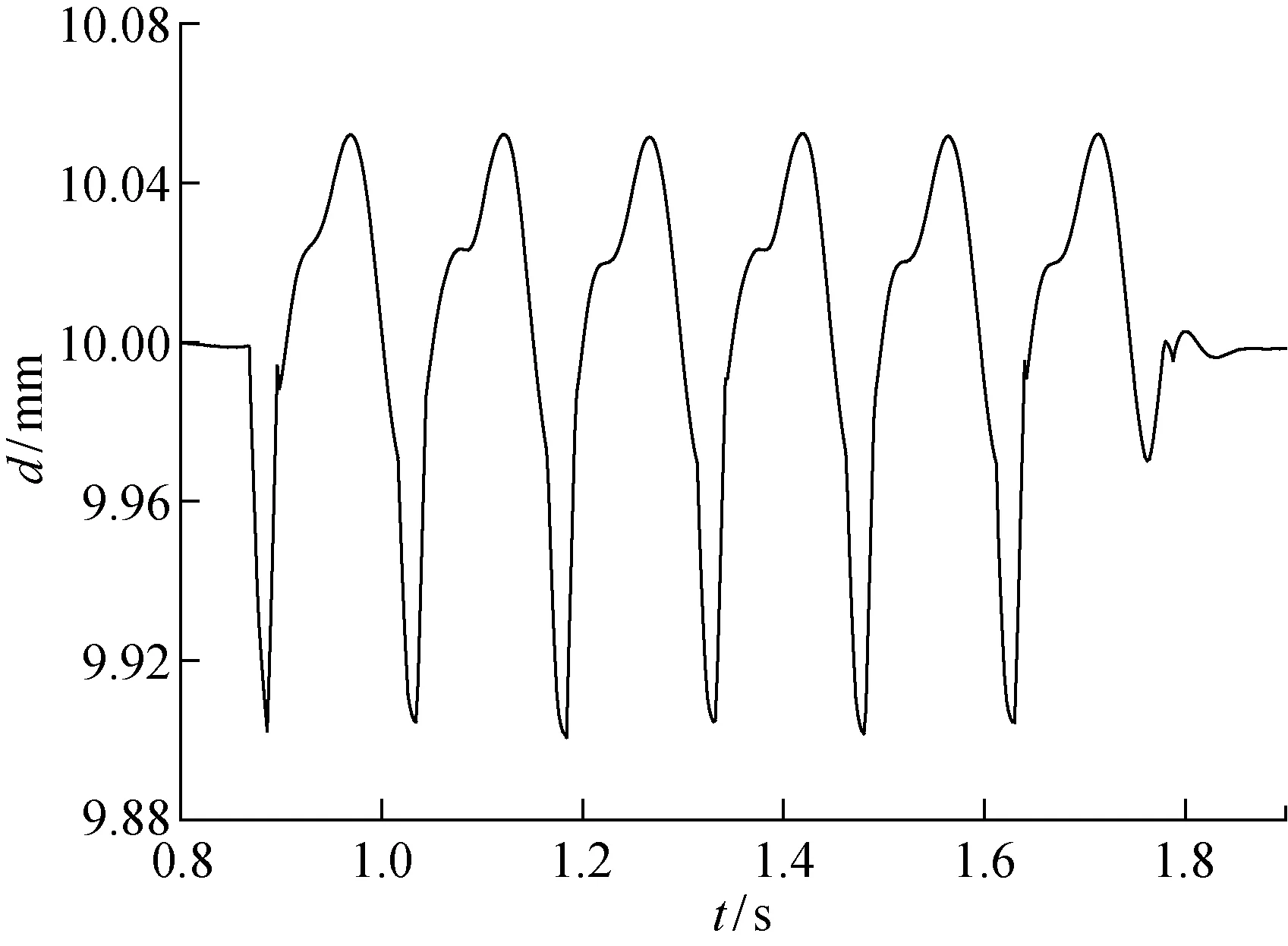
图10 电磁铁悬浮间隙时程曲线Fig.10 Time history curves of suspension gap of electromagnet

第1节转向架的加速度时程曲线(at-t图)和第1节车厢的加速度时程曲线(ac-t图)分别如图11、12所示.转向架竖向加速度变化在 -1～1.4 m/s2区间内波动，同电磁铁波动规律类似，磁浮转向架的加速度也是在轨道梁交界处波动较大.车厢的加速度波动区间为 -0.14～0.08 m/s2.对比图11、12可发现，车厢的竖向加速度峰值明显降低，这说明二系悬挂起到了很好的隔振效果.对于高速磁浮，磁浮列车竖向加速度限值一般取为0.4 m/s2[12-13].

图11 第1节转向架竖向加速度时程曲线 Fig.11 Time history curves of vertical acceleration for the first bogie

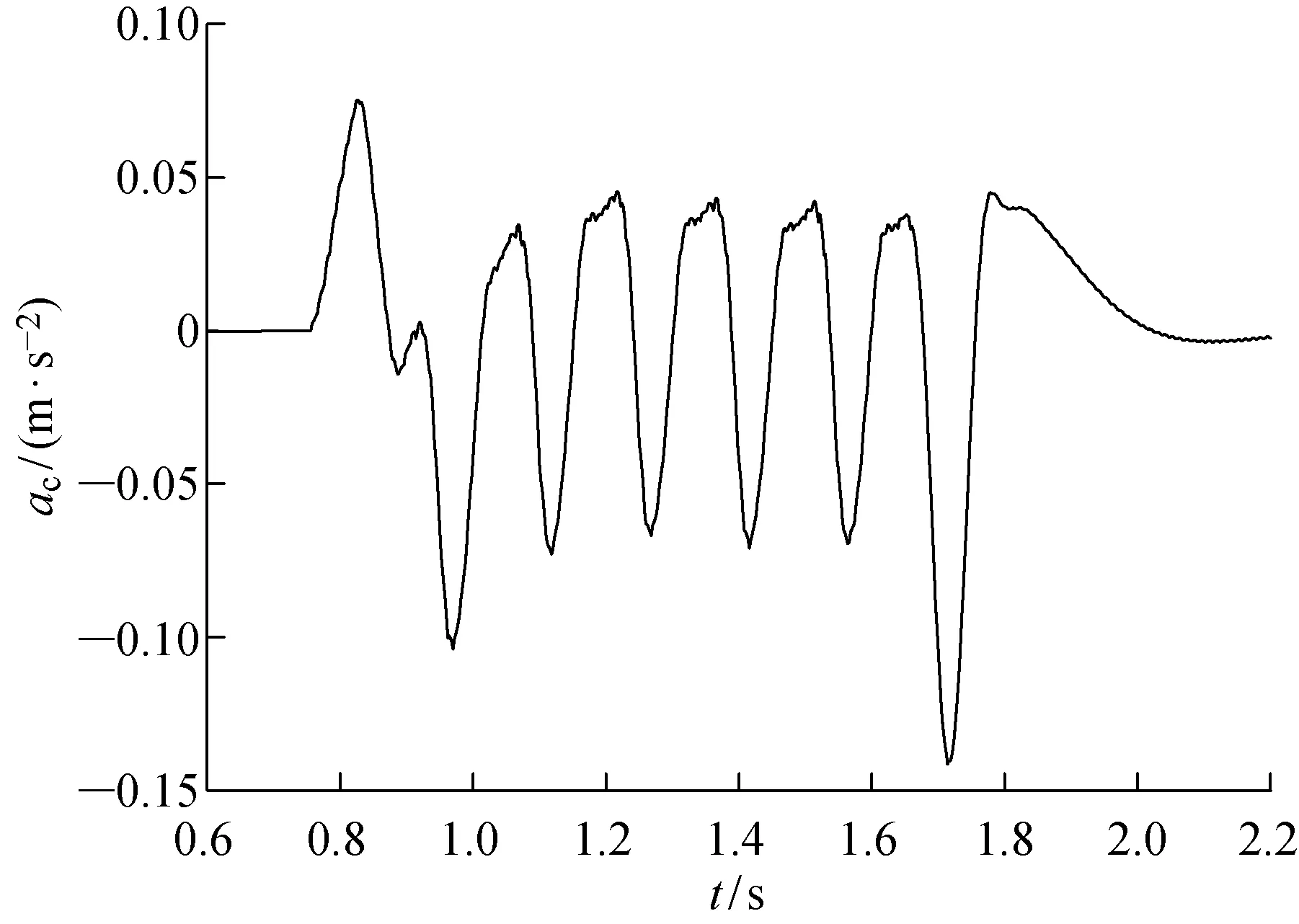
图12 第1节车厢竖向加速度时程曲线Fig.12 Time history curves of vertical acceleration for the first carbody

6.5 不同速度下仿真结果

本节通过计算和对比时速200～800 km/h磁浮列车和桥梁的动态响应，探究桥梁跨中位移和加速度峰值的变化规律、车体竖向加速度随列车速度的变化规律以及桥墩参振对动力耦合分析结果的影响.由图7可知，对于简支梁型多跨轨道梁而言，不同跨间的桥梁动力响应基本一致，所以可选取其中任意一跨进行分析研究，车辆方面主要考虑首车+中车+尾车的列车布置.

6.5.1轨道梁跨中位移 桥墩参振影响下的轨道梁跨中位移峰值随速度变化曲线(yb-v图)及其比较结果如图13所示，桥墩的参振作用对桥梁跨中动位移的影响较小.考虑桥墩的作用下，竖向刚度略小于不计入桥墩的情况，跨中位移峰值会增大，但增加幅度不明显；另一方面，随着车速的增大，桥梁跨中位移峰值对于速度的变化不敏感，在400 km/h左右轨道梁位移峰值会有一个小幅度的增大.总体而言，车速小于500 km/h时，跨中位移峰值处于一个较为平稳的状态，变化较小，车速大于500 km/h时，桥梁跨中动位移峰值会随着车速的增大有微小的增加.

图13 跨中位移随速度变化曲线Fig.13 Mid-span displacement versus speed

6.5.2轨道梁跨中加速度 轨道梁跨中竖向加速度峰值随磁浮列车运行速度的变化规律曲线(ab-v图)如图14所示.轨道梁跨中竖向加速度基本随速度的增大而增大，考虑桥墩参振的作用下，桥梁的刚度有所削弱，计算桥墩参振的跨中竖向加速度比不计入桥墩的跨中加速度峰值要偏大.在时速为600 km/h，考虑桥墩的情况下，跨中竖向加速度峰值增大了约13%，比较显著.通过对比表3轨道梁各阶模态频率的结果可以发现，桥墩对于低阶模态的影响非常微小，但是，对于高阶模态的影响比较显著，反映在轨道梁跨中竖向加速度峰值上有比较明显的变化.目前，磁浮轨道梁主要通过控制基频和跨中竖向位移峰值来实现刚度控制.从本节计算结果可以发现，考虑桥墩参振作用对于桥梁加速度动力响应的影响是比较明显的.

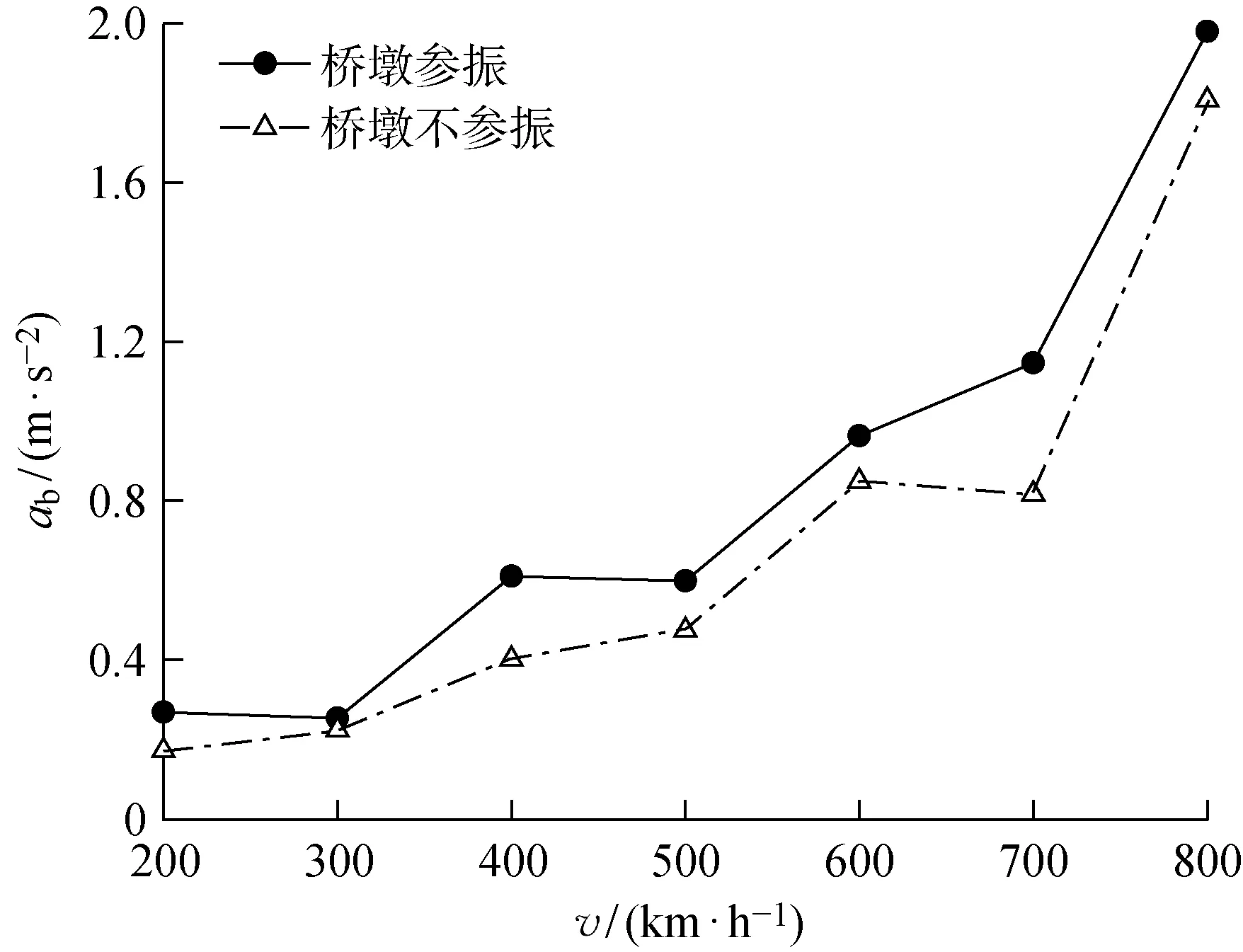
图14 不同时速下轨道梁跨中加速度峰值Fig.14 Peak acceleration at mid-span point at different speeds

6.5.3车体竖向加速度 取中车车体作为分析对象，中车车体竖向加速度峰值随磁浮列车运行速度的变化规律曲线(ac-v图)如图15所示.对于车体而言，车体的竖向加速度峰值基本随速度呈单调递增关系，且时速不超过800 km/h范围内，车体竖向加速度峰值均没有出现显著的陡升.计入桥墩的情况与不计入桥墩的情况比较，车体加速度峰值没有显著的变化，桥墩参振对车体加速度峰值的影响较小，几乎可以忽略.通过简支梁跨时，中车的加速度相较首车和尾车更小，且在时速不超过600 km/h时中车车体竖向加速度均小于0.4 m/s2；车厢的竖向加速度峰值出现在车辆入桥和出桥阶段，主要是由于在该位置由于桥墩的作用，竖向刚度变化明显，轨道梁截面的相对转角比较大.

图15 不同时速下中车的车体加速度峰值Fig.15 Peak acceleration of mid carbody at different speeds

7 结论

本文基于Simpack、ANSYS及Simulink这3个软件搭建了跨平台的耦合分析软件系统，并以与时速600 km/h高速磁浮配套的24.768 m轨道梁为仿真对象，针对超高速磁浮系统进行车桥耦合系统进行动力响应分析，得到如下主要结论：

(1) 磁浮列车的运行速度小于500 km/h的速度区间，轨道梁竖向位移峰值变化不明显.当时速超过500 km/h时，轨道梁的竖向位移峰值会随着车速的增大而显著增大；

(2) 考虑振动过程中的桥墩弹性变形对整体桥梁结构体系的刚度的影响，轨道梁的跨中位移峰值随车速变化很小，但是对轨道梁跨中加速度峰值的影响比较明显，在600 km/h时速大概有13%的差别.是否考虑墩柱作用对于车体加速度峰值影响较小，几乎可以忽略；

(3) 本文提出的基于多平台联合仿真计算方法，针对超高速磁浮-控制器-轨道梁耦合分析是可行的，可用于获取列车和轨道梁的动力学响应，具有良好的通用性和可扩展性.