基于数学建模的高中数学教学策略探究

张芝悦

[摘  要] 数学建模是深化数学概念、原理、定理等知识的理解和应用数学知识解决实际情境问题的基本手段. 文章在分析基于数学建模的高中数学教学原则的基础上，以《三角函数的应用》为例探究了基于数学建模的高中数学教学策略.

[关键词] 数学建模;高中数学;策略

高中数学教学不仅要注重相关概念和数学方法的深度理解，培养学生从日常生活中发现问题、分析问题的意识，而且也要理论联系实际，有效提高学生应用所学知识解决实际问题的能力. 而作为高中学生必备的数学核心素养之一，数学建模素养不仅能够培养学生应用数学语言表达实际问题的能力，而且也能反过来利用模型思想巩固所学知识，深化相关概念、原理、定理等知识的理解. 因此，以提高数学建模素养为核心，探究高中数学教学方式具有重要的意义.

[?]基于数学建模的高中数学教学原则

1. 激发兴趣原则

在高中数学建模素养培养中，教师應最大限度地让学生了解数学建模的魅力，使学生具有强烈的意愿自主地开展探究性学习. 例如，在教学《三角函数的应用》时，教师请学生扮演船长，并询问“船长”面对如下问题时该如何处理：“当货船航行到九江港时，你最想获得哪方面信息”“如何调查港口水深与日期时间的关系”“面对货船被搁浅的风险，如何选择合理的港口进出时间”，由此激发学生探究的兴趣，促使学生尝试解决实际问题中所蕴含的数学信息.

2. 联系实际原则

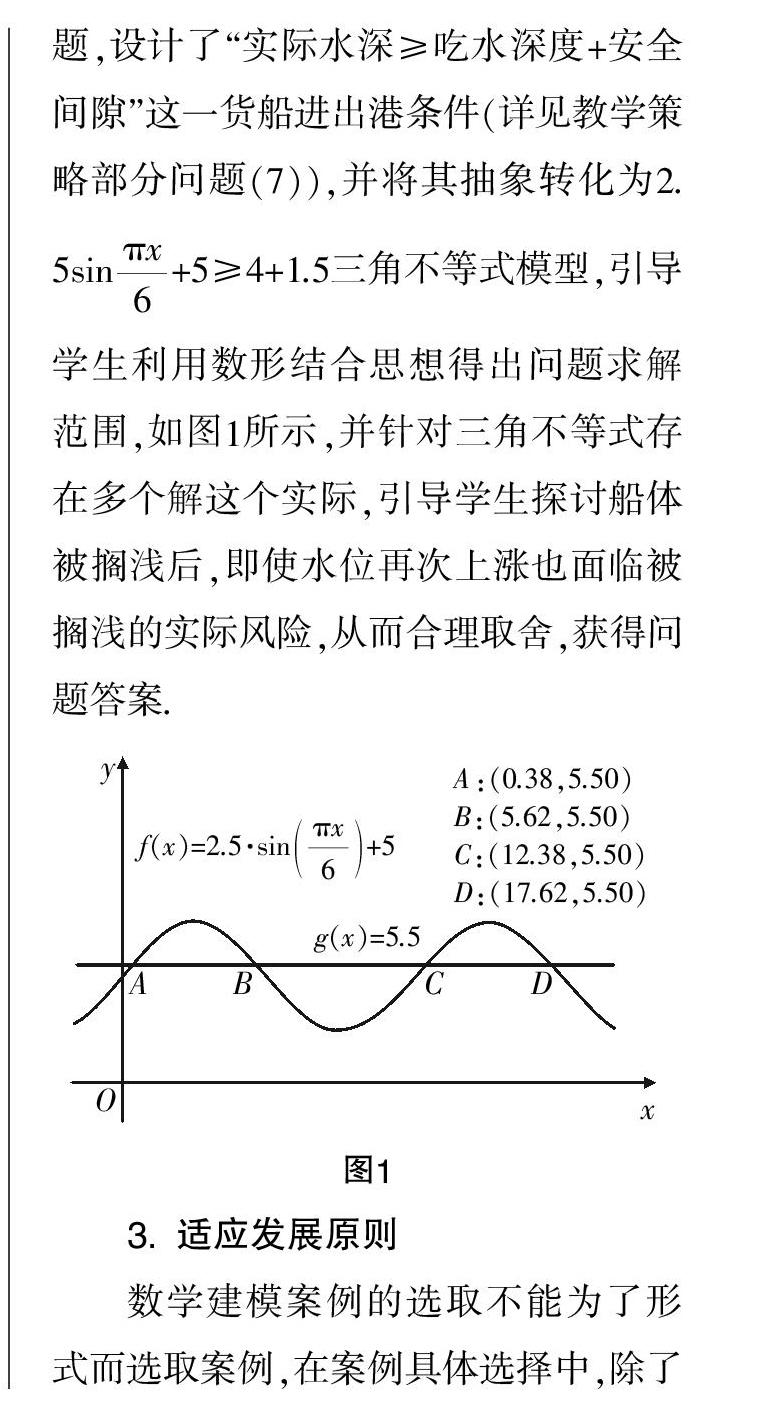
为了更加真实地刻画现实世界是高中数学建模的核心，因此，在设计和选择数学建模主题时，教师应从学生熟悉的日常生活场景着手，有效促使学生感受数学建模的真实性. 同时，教师还应及时引导学生发现问题，求解和验证所建立的数学模型，从而将教学中所学习到的知识与实际生活相联系. 例如，货船吃水深度是实际生活中经常所听到的概念，因此，教师应结合航行安全问题，设计了“实际水深≥吃水深度+安全间隙”这一货船进出港条件（详见教学策略部分问题（7）），并将其抽象转化为2.5sin+5≥4+1.5三角不等式模型，引导学生利用数形结合思想得出问题求解范围，如图1所示，并针对三角不等式存在多个解这个实际，引导学生探讨船体被搁浅后，即使水位再次上涨也面临被搁浅的实际风险，从而合理取舍，获得问题答案.

3. 适应发展原则

数学建模案例的选取不能为了形式而选取案例，在案例具体选择中，除了要满足学生的心理发展特征和智力发展水平外，还应遵循因人而异、适时发展的原则，在合理的教学阶段选择适当的现实问题. 例如，对于初次接触数学建模思想的学生，教师应重点培养学生应用数学知识描述现实问题的能力，注重将教材中的例题或习题进行改编;对于已经具备数学建模意识的学生，教师应将教学的重点放置在真实情景中抽象出数学概念和数学模型的能力;对于已经熟悉建模过程的较高阶段的学生，教师应选择较为完整的实际问题，及时引导学生经历数据收集、模型建立、模型验证、模型对比等过程，不断提升学生的数学建模素养.

[?]基于数学建模的高中数学教学策略

1. 创设问题情境，培养数学化能力

数学核心素养的提高必须借助数学化过程，并且缺乏问题情境的教学是空洞的，因此，教师应从学生实际生活出发，结合教学目标和所授内容，创设学生感兴趣的问题情境，促使学生找出现实情境与数学知识之间的规律与联系，并从数学的视角出发，应用数学知识和方法将其转化为数学问题加以分析.

例如，在组织学生学习完三角函数知识时，教师应根据所授内容，利用视频播放九江港码头涨潮时货船驶入航道停靠码头进行装卸，落潮时及时返回的生活场景. 在此基础上，设计如下问题串要求学生应用已学知识发现问题情境中所蕴藏的数学规律.

（1）货船为什么在涨潮时驶入航道，为什么在落潮时返回？

（2）假如你就是船长，你最想了解该港口哪方面的信息？

（3）如果让你调查港口水深与日期时间的关系，你会采用哪些方式？

（4）假如表1所反馈的是某一日九江港时间与水深之间关系，你能从中获取哪些有用信息？

2. 渗透建模思想，促进实践应用能力

思维品质与关键能力是数学核心素养的本质，而模型思想可以有效帮助学生理解数学概念、原理的本质与规律，解决现实生活中的某一类问题，并且，数学的实践应用能力正好体现了数学建模素养的关键能力，因此，教师应按照“生活问题—建立模型—求解模型—解释结果”的思路，不断渗透建模思想和方法，促使学生有效体验完整的数学建模过程. 值得强调的是，由于课时的有限性，教师应将数据的收集等过程最大限度地留置在课外交流合作中完成.

例如，在上述问题情境创设和实际问题数学化之后，教师应及时通过如下教学方式渗透建模思想与方法.

（5）我们学习过的函数模型有哪些，能否应用相关数学模型描述九江港水深与时间的变化关系？

（6）在直角坐标系中画出以上数据的散点图，并计算相关函数模型.

3. 注重回顾反思，提升创造迁移能力

数学的学习是理解与反思的过程，学生有了疑惑才能主动深入地探究和思考，并且数学建模还是一个循序渐进的过程，因此，教师应及时引导学生反思建模过程，鼓励学生大胆地提出自己的猜想和疑惑，启发学生提出新的问题.  同时，教师还应帮助学生通过思维导图等方式组织学生及时进行归纳总结，有效培养学生的知识迁移能力. 仍以上述案例教学为例，在上述相关函数模型获得之后，为了研究的深入，教师还应设计如下问题及时引导学生不断回顾反思，促进学生数学建模素养的提高.

（7）由于每艘货船的吃水深度是不同的，并且根据安全规定船只航行时其船底与河道之间的距离必须大于1.5米，若有一艘吃水为4米的货船，试问该船什么时间才能驶入港口，在港口最多能停留多长时间才能不被搁浅？

（8）已知某一货船14：00开始装卸货物，若吃水深度以0.3 m/h的速度下降，并且其他条件同上述问题（7），为了防止该船被搁浅，试问这艘货船必须在何时之前停止装卸驶向更深水域？

4. 多元化过程性评价，提高合作探究能力

简单的应用题测试无法激发学生数学建模探究的兴趣，也无法在数学建模教学中起到良好的教学效果，并且，学生对同一问题的理解是不同的，因此，教师应摒弃以成绩为唯一标准的评价体系，实施多元化和多样化教学评价，注重学生自评、互评、开放题的测试、小论文等形式，有效掌握数学建模中学生思维品质、关键能力以及存在的不足. 特别是对于学生数学建模过程中暂时找不到问题解决思路和方法的学生教师应及时给予鼓励和指导，帮助其树立信心;对于学生数学建模过程中呈现出的创造性建议教师应及时给予肯定.

例如，在上述案例中，教师可以从以下几个方面进行多元化的过程性评价：

①学生讨论发言、结果汇报中的表现;②数据收集、分析的方法是否合理;③模型的建立是否符合案例实际;④建模过程中解决困难的机制和办法;⑤模型反思，或提出新的探究问题;⑥小组合作和计算过程中学生的状态.

总之，教学活动中，教师应充分发挥学生这一数学建模活动的主体作用，通过创设问题情境、引导学生建立和求解数学模型、贯穿过程性评价、注重回顾反思等策略，有效提升学生的数学化、合作探究、实践应用等能力.