用问题驱动学生探究学习数学

庄秀英

摘 要：驱动学生探究学习数学，是数学教师的主要职责。问题是驱动学生探究学习数学的“工具”，在实施初中数学教学的时候，根据教学内容设计问题，根据教学过程提出问题，使学生们在有效问题的驱动下，自主、合作地进行探究，不仅可以理解数学内容，还可以锻炼学习能力。文章具体介绍设计数学问题和应用数学问题的策略，以为其他一线的初中数学教师提供驱动学生探究学习数学的经验。

关键词：初中数学;问题驱动;设计问题;应用问题;探究学习

在新一轮课程改革实施过程中，数学课程发生了显著的变化，“问题性”是具体的变化表现。这一变化表明，数学教学注重“问题”教学。《义务教育数学课程标准（2011年版）》中明文要求教师：善于设计、提出问题，用问题驱动学生探究学习。此要求是契合数学课程的“问题性”的。所以，在实施数学教学的时候，教师要将“问题”作为工具，有效地开展创设教学活动。问题驱动式教学是實现这一目标的主要方式。

所谓的问题驱动式教学是指联系教学内容，有效地设计问题;根据教学进度，有针对性地提出问题，用问题点燃学生思维积极性，驱动学生多样探究数学，使学生通过思考解决问题，理解数学内容，锻炼学习能力的教学方式。

立足数学课程特点和课程标准要求，在组织初中数学教学的时候，笔者对问题驱动式教学法进行了应用。笔者将从问题驱动式教学法的特点入手，从设计数学问题和应用数学问题这两方面入手，具体阐述应用问题驱动式教学法实施数学教学的策略。

一、 设计数学问题，做好驱动学生探究学习准备

有效地设计数学问题，是问题驱动式教学法的重要组成部分，也是引导学生们探究学习数学的基础。在实施数学教学之前，笔者会先分析教学内容和学生学情，有针对性地设计出不同的数学问题。

（一）有目的地设计数学问题

设计、应用数学问题，是为实现数学教学目的服务的。所以，教学目的是教师设计数学问题的依据。有目的地设计数学问题，教师需要紧扣教学目标和教学内容，使学生们通过解决问题，实现不同的目的，由此提高数学教学效果。

以“多边形及其内角和”为例，本节课的教学目的之一是引导学生们把握新旧知识联系，将多边形转化为三角形，借此总结出多边形的内角和。立足此目的，在组织课堂教学之前，笔者先行设计了如下问题：

问题一：三角形和四边形的内角和各是多少？

问题二：我们在学习三角形和四边形的时候，是如何探究出它们各自的内角和的？

问题三：是否可以使用此类方法探究出五边形的内角和呢？

问题四：在将五边形转为三角形的过程中，可以得到多少个三角形呢？如果对六边形、七边形，乃至n边形进行转化，可以获得多少个三角形呢？

问题五：根据操作情况，说一说多边形的内角和、获得的三角形以及多边形自身的边数之间有何关系？

问题六：根据获得的关系，是否有更为简单的方法对多边形进行转化呢？有哪些方法呢？

由此可见，这些问题是以多边形转化为三角形为过程，以探究多边形的内角和为目的的。在课堂上，教师根据学生们的问题思考情况，一个个地提出问题，可以驱动他们一步步地深入探究，通过迁移知识，获取探究数学新知的方法，提高课堂学习效果。

（二）有探究地设计数学问题

引导学生探究学习数学，是设计数学问题的依据。当设计出的数学问题缺少探究性的时候，很难获得预期的教学效果。所以，要想有效地发挥数学问题的价值，在课前，教师要根据教学内容，设计出具有探究性的问题，引发学生思考。

以“角的平分线的性质”为例，探究作角平分线的方法是学生们在课堂上要完成的一项任务。此项任务本身是具有探究性的，为教师提供了设计探究性问题的便利。在实施课堂教学之前，笔者根据此项探究任务，设计如下问题：

问题一：你有什么方法绘制出一个角的角平分线呢？（引导学生初步探究，增强探究兴趣）

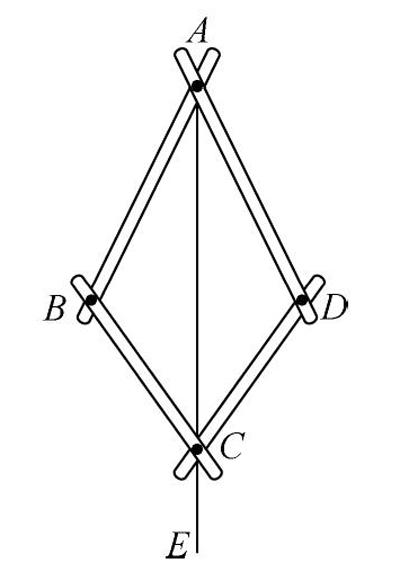
问题二：有这样一个平分角的仪器，如下图所示：

已知AB=AD，BC=DC。点A是角的顶点。连接AE，此时∠BAE=∠DAE，这表明AE是∠DAB的角平分线。你是否能证明AE是∠DAB的角平分线呢？

问题三：通过探究以上两个问题，你获得了哪些发现呢？能否自主地利用尺规作图来展现已知角的角平分线呢？如何作图呢？

如此设计的问题，是以探究角的平分线为主要目的的，具有探究性。受到问题的驱动，学生们有针对性地进行探究，可以逐步地探究到角平分线的做法，完成学习任务，达到预期的课堂探究效果。

（三）有层次地设计数学问题

学生探究学习数学，是指全体学生探究学习数学。在传统的数学教学中，部分教师忽视学生的探究水平，机械地提出数学问题，使得数学问题成为部分学生探究学习数学的“工具”，导致另外一部分学生难以有效地探究学习数学，不仅影响了课堂教学效果，还拉大了学生们之间的差距。如此做法，有违素质教育理念。要想引导全体学生探究学习数学，教师需要根据不同学生的探究学习情况，有针对性地设计问题。有层次地设计问题是实现这一点的主要途径。

以“等腰三角形”为例，在学生们理解了新知内容后，教师需要提出问题，引导学生们对所学进行应用，通过解决问题巩固所学。联系教学经验和学生们的学情，在实施教学之前，笔者先有层次地设计了不同难度的问题。

问题一：已知一个等腰三角形的底边长是5，腰长是2，请问这个等腰三角形的边长和是多少？

问题二：已知一个等腰三角形的两条边的长度分别是25和22，请问剩下的一条边的长度会是多少呢？

问题三：已知一个等腰三角形的两条边分别是6和8，请问它的周长是多少呢？

如此设计出的问题，是先易后难的。在课堂上提出问题，可以使学生们根据自身的学习情况，选择不同难度水平的问题。学生通过解决问题，实现对的等腰三角形基础内容的有效掌握。尤其，一些学习水平不高的学生，因为解决了三个问题，会获得学习满足感，提高数学学习积极性。另外一些学习水平高的学生，会受到其他水平学生的激励，端正学习态度，深入探究数学，实现数学学习发展。不同水平学生的数学学习发展，将促进数学教学效果的提高。