Caputo 型分数阶三维自治系统在相空间中的动力学行为
张宏杰,芮伟国
(重庆师范大学 数学科学学院,重庆 401331)
分数阶微积分的概念与经典的整数阶微积分的概念几乎诞生于同一个时代,即Leibniz 时代,然而分数阶微积分由于长期缺乏应用背景和相应的数学运算方法,其发展历程异常艰辛且非常缓慢,但随着几代科研人员和数学家们的不断投入研究,该境况得到了极大的改善. 特别是近几十年以来,随着分数阶微积分在反常扩散研究领域,信号和图像处理领域、控制理论、粘弹性力学、流变学以及生物科学等众多领域和学科之中得到了非常广泛的应用,人们对分数阶微分系统的研究越来越感兴趣,而且这类研究倍受国内外学者的关切,从文献[1~16]以及这些文献中所引用的其他大量文献可窥其一斑. 从另外一个层面来讲,由于自然界和工程中存在大量的分数维现象,经典整数维理论已经不再适用于这些问题的描述和解决,故人们只好引入分数阶微积分理论取而代之,使之不再受整数维度的限制,这也是分数阶微分系统越来越受到人们重视的主要原因. 但是,相对于经典的整数阶微分方程而言,分数阶微分方程的求解研究工作却变得十分困难,目前大多数关于分数阶微分方程的研究工作主要集中在正解的研究[17-18]以及解的存在性、稳定性和数值模拟等方面. 本文的工作将立足于分数阶动力系统在相空间内的动力学行为研究,即在相空间内平衡点随参数变化而变化的情况以及在平衡点邻域内系统的相轨线的动力学性态研究,这些研究与上述文献中的研究内容大不相同.
本文拟通过非奇异的线性变换和Laplace 变换,并借助于Mittag-Leffler 函数的敛散性,较为全面和深入地探讨下列Caputo 型分数阶三维自治系统


1 非奇异线性变换下系统(1)的标准型约化

即

类似地,可求得:

下,系统(1)被约化成标准型

综上所述,三维分数阶自治系统的线性变换相较于二维分数阶线性变换复杂了许多,我们不禁思考,在三维分数阶系统平衡点的类型以及相应的动力学行为较二维系统而言又有哪些异同之处呢?平衡点邻域内轨线的动力学性态又会发生怎样的改变呢?详情请参见第2 节的讨论.
2 系统的平衡点类别及其邻域内轨线的动力学性态和空间图貌
由于线性变换不改变系统的动力学性质和动力学行为,因此系统(1)及其对应的标准型系统的动力学性质和动力学行为是一样的. 为此,本节中我们仅讨论第1 节提供的标准型系统的平衡点的类别以及平衡点邻域内轨线的动力学性态.

以图1(a)为例,将其分别投影到3 个坐标平面 ξoη, ξoδ, ηoδ 上,得到图2(a),(b),(c)(图2 中 ξ的坐标单位长取1×1010). 不难发现二维平面图图2 中(a),(b),(c)中的原点均是稳定的,且是渐近稳定的,其平衡点类型为稳定结点. 同样地,我们可以类似地分析图1(b)的坐标投影(这里省略),也可以得到平衡点类型是不稳定的结点的结论. 因此,当 λi<0 (i=1,2,3) 时,我们称原点 ( 0,0,0) 为三维空间中的稳定结点;当λi>0 (i=1,2,3) 时,我们称原点 ( 0,0,0) 为三维空间中的不稳定结点.

图1 同号相异实特征根情形下系统(25)的空间相图Fig. 1 The phase portraits of the system (25) under different real characteristic roots with same sign
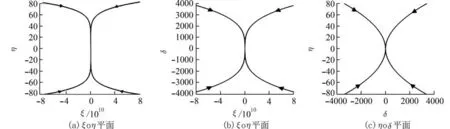
图2 同号相异实特征根情形下系统(25)的空间相图投影图Fig. 2 The map of phase portraits of system (25) under different real characteristic roots with same sign
情形2 当 λ1,λ2,λ3为异号相异实根时,系统(1)的线性变换与标准型及其解的表达式与情形1 完全一样,只不过其中 λ1,λ2,λ3的符号不尽相同罢了.
例如 当 λ1<0 <λ2<λ3时,则有 ξ (t)→0,η(t)→+∞,δ(t)→∞(t→+∞), 因而在此种情形下自治系统的零解是不稳定的;当 λ1>0 >λ2>λ3时,有 ξ (t)→∞,η(t)→0,δ(t)→0(t→+∞),从而该系统的零解仍是不稳定的. 因此,可以得到在该情形下系统(1)的零解都不稳定这一结论,现绘制出系统(26)的空间相图,见图3(a)与(b).
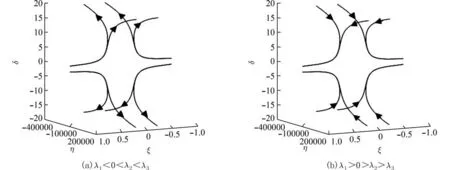
图3 异号相异实特征根情形下系统(25)的空间相图Fig. 3 The phase portraits of system (25) under different real characteristic roots with different sign
以图3(a)为例,将其分别投影到 ξ oη, ξoδ, ηoδ 平面上,得到其二维平面相图,见图4(a),(b),(c).
结合二维平面中奇点的性质与轨线走势,不难看出图4 中(a)和(b)图在二维平面中的平衡点类型为鞍点,具有不稳定性质(从图3 也可以直观地看出这一性质),而图4(c)图在其二维平面中平衡点的类型为结点. 因此,在三维空间中,我们将这样类型的平衡点( 0,0,0) 称为鞍-鞍-结型奇点,其具有部分稳定的特性.
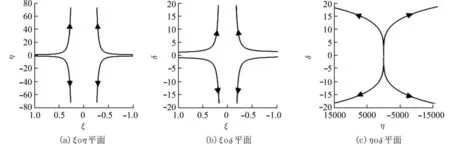
图4 异号相异实特征根情形下系统(25)的空间相图投影图Fig. 4 The map of phase portraits of system (25) under different real characteristic roots with different sign
情形3 当特征根 λ2=λ3为二重实根时,系统(1)经线性变换(21)化成下列标准型

通过Laplace 变换求得系统(28)的解为

以图5(a)为例,将其投影到三个坐标平面上,得到图6(a),(b),(c).
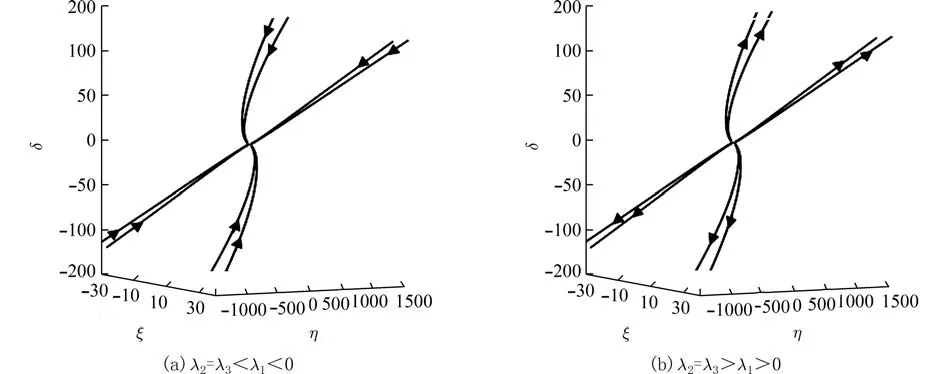
图5 特征根为二重实根的情形下系统(28)的空间相图Fig. 5 The phase portraits of the system (28) under double real characteristic roots
从图6 以看出在3 个二维投影平面上零解均是渐近稳定的,这一结论也可以通过解(27)式的渐近性质得到验证,且在此投影下,图6(a)和(b)平衡点的类型为结点,图6(c)的平衡点类型为退化结点. 同样地,在图5(b)下也可以获得相应的投影,且得到的图形会与图6(a),(b),(c)形状相一致,只是轨线走向刚好相反,即平衡点类型不发生改变,但其稳定性相反.
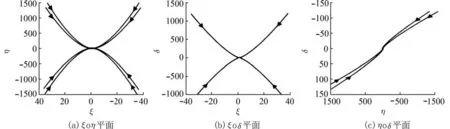
图6 特征根为二重实根的情形下系统(28)的空间相图投影图Fig. 6 The map of phase portraits of system (28) under triple real characteristic roots
情形4 当特征根 λ1=λ2=λ3=λ 为三重实根时,可分为以下2 种情况:
(1) λ 为三重实根,且a2,a3,b3≠0,微分方程组在其线性变换(23)下的标准型为

对(30)式施行Laplace 变换求得其解:
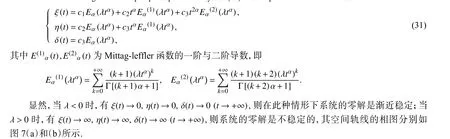
同样地,以图7(a)为例,将其分别投影到坐标平面 ξoη,ξoδ,ηoδ 上,得图8(a),(b),(c). 不难看出,图8(a),(b),(c)在二维平面上平衡点的类型均是退化结点,且具有渐近稳定的性质. 反之,若将图7(b)分别投影到3 个坐标平面,图形形状不发生改变,但是轨线走势与之相反,即平衡点类型仍为退化结点,但是不再具有稳定性这一性质,这也可以由 ξ (t)→+∞, η(t)→+∞, δ(t)→+∞(t→+∞) 看出.
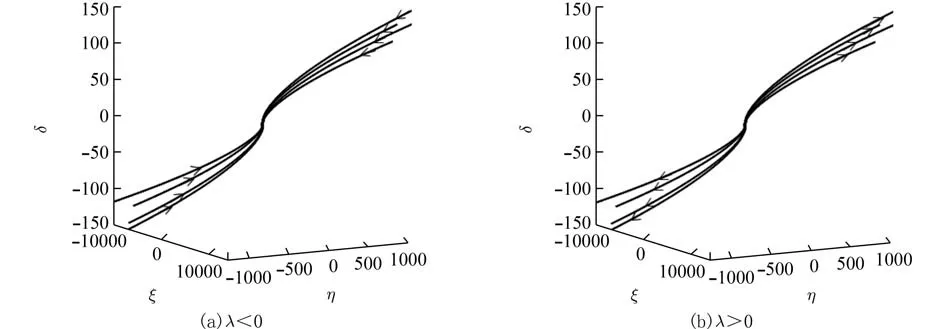
图7 三重实特征根情形下系统(30)的空间相图Fig. 7 The phase portraits of system (30) under triple real characteristic roots
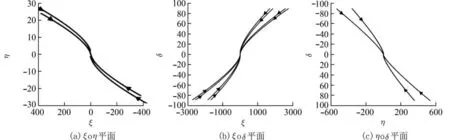
图8 三重实特征根情形下系统(30)的空间相图投影图Fig. 8 The map of phase portraits of system (30) under triple real characteristic roots
(2) λ 是三重实根,且a2,a3,b1,b3,c1,c2均为零时,系统(1)本身就是标准型:
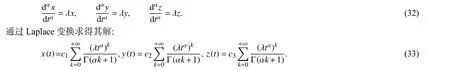
当 λ >0 时,显然有x(t)→∞,y(t)→∞,z(t)→∞(t→+∞), 故平衡点 ( 0,0,0) 是不稳定的;而当 λ <0 时,由于x(t)→0,y(t)→0,z(t)→0 (t→+∞), 则平衡点 ( 0,0,0) 是稳定的. 其空间轨线性态如图9(a),(b)(图9中 ξ, η, δ的 坐标单位长为1×1021). 此时,我们称平衡点 ( 0,0,0) 为空间的临界结点,当 λ >0 时,为不稳定结点;当 λ <0 时,为稳定结点.
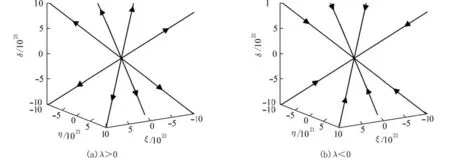
图9 三重实特征根情形下系统(32)的空间相图Fig. 9 The phase portraits of system (32) under triple real characteristic roots
——如何培养学生的创新思维

