幂级数收敛半径和收敛域的求解探讨
——如何培养学生的创新思维
2020-03-07 13:04:02刘洋
数理化解题研究 2020年6期
刘 洋
(广东省佛山市广州工商学院三水校区 510850)
一、幂级数的收敛半径
关于此幂级数的收敛半径的求法可直接利用下面的定理.

二、不同类型的幂级数收敛半径和收敛域的求法
本文对标准型幂级数求它们的收敛半径和收敛域的求解进行研究.幂级数的形式多样,不同类型幂级数的求解方法各异,但本文主要把不同类型幂级数通过换元的方法化为标准型幂级数后,再进行求解.
(2)求收敛域(即考察端点x=±R的敛散性).


2.“一般型”化为“标准型”的求法
通过换元将“一般型”化为“标准型”,利用标准型求解.

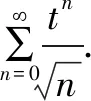
综上,原级数的收敛域为[4,6),收敛半径R=1.
3.“有缺型”化为“标准型”的求法
通过逐项积分或逐项求导或换元将“有缺型”化为“标准型”,利用标准型求解.


三、归纳总结一般规律


(3)求收敛域(即考察端点x=±R的敛散性).由于求收敛域和收敛半径题目类型多样,为更好更快地解决问题,需要按“标准型”、“一般型”和“有缺项”三种类型求解.在上述过程中我们以“标准型”、“一般型”和“有缺项”三种类型的三个例题通过换元化为“标准型”来具体说明求收敛域和收敛半径的求解方法,最后总结出一般的规律.
本文利用现有的有用信息定理1,举例讲解例1,让学生自己去理解体会标准型幂级数求解收敛半径和收敛域的步骤,进一步探索和想出可供选择的信息进行考虑不同类型的幂级数的求解方法.本文中幂级数收敛半径和收敛域的求解方法按不同的类型化归同一种类型求解的对分课堂,不仅激发了学生学习数学的兴趣,而且还培养了学生的创新思维.
猜你喜欢
高校应用数学学报A辑(2020年2期)2020-07-07 02:38:46
中国药房(2019年9期)2019-09-10 07:22:44
天水师范学院学报(2018年2期)2018-06-19 06:28:44
现代职业教育·高职高专(2018年5期)2018-05-14 16:20:39
课程教育研究·新教师教学(2015年9期)2017-09-26 22:36:47
中国校外教育(中旬)(2017年2期)2017-04-10 02:22:41
课程教育研究·学法教法研究(2016年33期)2017-03-30 21:05:28
哈尔滨理工大学学报(2016年2期)2016-09-12 18:46:35
考试周刊(2016年54期)2016-07-18 08:03:33
艺术评鉴(2015年8期)2015-05-11 01:25:48

