如何在高中数学教学中培养学生的思维能力
吴潘钰
(江苏省海门市四甲中学 226100)
思维能力涉及的范围较为宽泛,平时所说的分析、概括,比较等都属于思维能力的范畴,其关系着学生学习成绩的提升,因此授课中应充分认识到思维能力的重要性,认真回顾以往教学实践,积极总结相关的培养策略,不断提高培养质量与水平,为学生更好地学习数学知识奠定坚实基础.
一、讲解例题,做好解题思维引导
培养学生思维能力的方法多种多样.对高中数学科目而言,做好例题讲解,积极引导学生的解题思维,是一条不错的途径,因此授课中,一方面,做好授课内容分析,结合以往经验,用心筛选例题,确保例题在巩固所学的同时,能够给其思维带来启发,打破定势思维带来的影响,提高其思维的灵活性,真正做到灵活运用所学,具体问题具体分析.另一方面,讲解例题前,先留下充足的思考时间,鼓励学生尝试着进行解答,而后引导其回顾所学,认识解题中的思维漏洞,及时完善解题过程,启发其思维的同时,能够使其在分析问题时更为严谨.
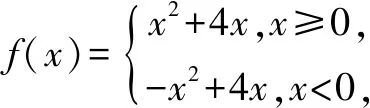
A.恒为正 B.恒为负
C.恒为0 D.无法确定
该例题以函数为背景,较为抽象,可很好地锻炼学生的抽象以及推理思维.认真审题,充分挖掘题目中的隐含条件是解题的关键.认真回顾所学,并结合解题经验,解题时需要判断函数f(x)的奇偶性和单调性.根据所学知识不难判断出f(x)在R上是单调递增的奇函数.由a+b>0,b+c>0,c+a>0可知,a>-b,b>-c,c>-a,即f(a)>f(-b),f(b)>f(-c),f(c)>f(-a),所以f(a)+f(b)>0,f(b)+f(c)>0,f(a)+f(c)>0,即f(a)+f(b)+f(c)>0,正确选项为A.
通过该例题的讲解,使学生意识到解答函数试题时,为提高解题效率,应牢固掌握有关函数的基础知识,注重自身抽象思维以及推理思维的训练,以实现高效解题.
二、创设情景,加强思维能力训练
提升学生思维能力时,应注重创设相关问题情景,对学习者的思维进行训练.授课中,使其充分把握每次训练机会,能够及时认识到训练中的不足,积累相关的思维技巧,在解答相关高中数学问题时,能够少走弯路,实现解题效率的提高.一方面.保证创设问题情景的质量.高中数学试题情景灵活多变,应结合学生不易理解的知识点设计相关问题.保证设计的问题具有较强代表性,又能很好的锻炼学生的思维能力.另一方面,训练中做好点拨.要求学习者认真分析解题过程,思考能否从另外的角度解答问题,提高解题效率与思维的灵活性.
例2已知当x∈[1,3]时,不等式|2a-x|≥a-1恒成立,求a的取值范围.

授课中讲解该题目的目的在于,针对常规高中数学题型既要掌握通法通解,又要不满足于得出正确结果,注重运用创新思维寻找最佳的解题思路,进一步提高解题效率.
三、优选习题,注重思维能力拓展
高中数学授课中,仅仅要求学习者做一些基础试题,不利于学生思维的有效提升,应结合授课的重点与难点,优选习题,积极拓展学生思维,使其能够灵活运用所学分析、解答各种数学问题.一方面,鼓励学生在学习中做一个有心之人,注重常见习题类型的归纳,明确不同题型的解题思路,理顺解题思维,解题中能够及时找到突破口.另一方面,选择较为新颖且具有一定难度的习题,要求学生进行分析解答.在锻炼学生提取信息、转化信息能力的同时,使其更好地把握数学知识的外延,深化理解的同时,实现思维能力的进一步拓展.



通过该题目的讲解,使学生认识到转化思维是一种重要的数学思维,在日常的学习与解题中认真总结转化方法与技巧,注重将新颖的、陌生的问题转化为熟悉的、易于解答的问题,以实现成功求解的目的.
总之,高中数学授课中,培养学生的思维能力具有重要的现实意义.良好的思维能够使学生在最短的时间内找到解决问题的有效方法,因此授课中,应充分认识到自己的重要性,做好合理的教学安排,认真落实思维能力培养工作,不仅是学生牢固掌握所学,而且能够积极动脑,实现所学知识的灵活应用.

