核心素养下的高中数学教学探究

王志伟

(江苏省常州市金坛区金沙高级中学 213200)

数学核心素养是数学课程目标的集中体现，对数学课堂教学具有指导和引领作用，数学核心素养反映了数学的本质，数学思维和数学思想方法，通过数学的学习和应用过程，逐步形成学生的思维品质，关键能力，体现数学学科的育人价值.这就要求我们的课堂教学必须围绕核心素养而展开，为素养而教，用学科育人.那么，如何在课堂教学中培养学生的学科素养呢？结合“函数的和，差，积，商的导数”一课的课堂教学实录，就数学核心素养在课堂教学中的渗透作了一些尝试和思考.

一、课前思考

“函数的和，差，积，商的导数”的重点在于让学生掌握求导法则，并能灵活运用，因此在以前的教学中，我们往往采用如下教学方法：首先由教材例题求y=x2+x的导数的讲评分析，归纳出函数的和的求导法则，然后直接列出其他求导法则，分析其结构特征，并要求学生记忆，然后通过大量的练习，着重讲授求导法则的应用.这样的课堂教学，教师讲得非常轻松，效果也不错.但仔细想想，这种课堂虽然看上去非常流畅，但缺少数学的“灵气”，有点要把学生训练为“数学操作工”的意味，学生的数学思维，数学思想方法等得不到锻炼，体现不了数学的内涵，核心素养的渗透更是无从谈起.课堂教学还是要遵循新课程理念，从长远考虑，不能急功近利，要切实提高学生的数学能力.因此，本节课准备改变教学策略，侧重求导法则的探究，在探究过程中穿插求导法则的运用.在知识的生成过程中，培养学生发现问题，分析问题，解决问题的能力，锻炼学生的数学思维.

二、教学过程片段

师：问题1，y=x2+x的导数是什么？

生1：y′=2x+1.

师：你是怎么得到的？

生1：利用导数的定义.

师：很好，这个结论是正确的，再来观察一下，这个函数的导数与函数的各项之间有什么关系？

生2：(x2)′=2x,x′=1,故(x2+x)′=2x+1.

师：很好，你能不能推广到一般形式呢？

生2：应该是两个函数的和的导数，等于这两个函数的导数的和.

师：我们知道，猜想到的不一定正确，需要严格的证明，你能证明吗？

生2：利用定义证明(略).

师：这样我们得到求导

法则1：

[f(x)+g(x)]′=f′(x)+g′(x)(板书).

师：问题2，如何求y=3x2的导数.

生3：利用导数的定义，可以求出y′=6x.

师：很好，你能不能借助法则1来求出它的导数？

生3：将y=3x2看成y=x2+x2+x2，(x2)′=2x,(3x2)′=2x+2x+2x=6x.

师：推广成一般形式呢？

生3：c·f(x)就是c个f(x)相加，所以[cf(x)]′=cf′(x).

师：这样得到求导

法则2：

[cf(x)]′=cf′(x)(板书).

师：问题3，你能不能利用法则1和法则2，推导出[f(x)-g(x)]′=？

生4：[f(x)-g(x)]′=[f(x)+(-g(x))]′=f′(x)+(-g(x)′)=f′(x)-g′(x).

师：可以看出：两个函数的差的导数，等于这两个函数的导数的差，即

[f(x)-g(x)]′=f′(x)-g′(x)(板书).

师：问题4，函数的积的导数是否也等于导数的积呢？

(有同学认为是对的，有同学略作思考后认为是错的)

生5：我认为是错误的，可以找一个特例：如：函数y=cf(x)，把常数c看成函数g(x)，这样y=cf(x)可以看成y=f(x)·g(x)，如果函数的积的导数等于导数的积，那么[cf(x)]′=c′·f′(x)=0·f′(x)=0，与[cf(x)]′=cf′(x)矛盾.

师：很好，这个结论是错误的.能不能猜想出函数的积的导数的求导法则吗？

(学生陷入沉思，部分同学在讨论，验证)

师：(点拨)是否可以利用刚才同学的思路，从两个函数的形式上考虑？

生6：把常数c看成函数g(x)，这样y=cf(x)可以看成y=f(x)·g(x)，由[cf(x)]′=cf′(x)，故[f(x)·g(x)]′=f′(x)·g(x)，但我利用特例x3=x·x2来验证，这个结论不正确，应该少了什么？

师：生6讲得很有道理，哪位同学帮他解决这个疑惑呢？

生7：从对称的角度看，f(x)与g(x)的地位相同，应该还有f(x)·g′(x)项，但由于常数的导数等于0，即g′(x)=0，所以才有[cf(x)]′=cf′(x)，因此可以猜想[f(x)·g(x)]′=f′(x)·g(x)+f(x)·g′(x).

师：请同学们找几个特例来验证一下，看看结论是否正确.

(学生尝试后，点头认同)

师：生7讲得非常好，他从两个函数的地位完全相同的角度考虑，得到求导后的形式也应该是一样的结论，合情合理，这样我们得到

法则3：[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)(板书).

这个结论的证明我们留在课后完成.

师：问题5，你能否根据函数积的求导法则，猜想一下函数的商的求导法则呢？.

(大家在思考讨论，大概5分钟后，有一位同学站了起来)

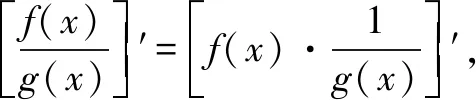
令g(x)=x，

因为x′=1，所以可以猜想：

我找了几个特例验证了一下，都是正确的.

师：生8的思路非常清晰，猜想有理有据，而且他最大的闪光点在于，不是两个函数都用特例来处理，而是一个用特例，一个用抽象函数f(x)表示，这样在猜想商的求导法则时，比较容易找到特征形式.

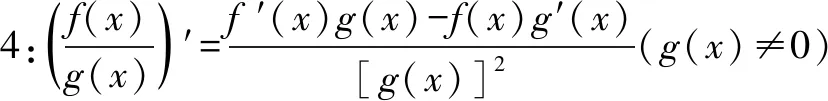
有了这些求导法则后，我们将基本初等函数的求导推广到由基本函数的四则运算构成的函数的求导公式，简化了我们的运算，可谓意义深远啊！(略)

三、教学反思

这节课通过具体的，学生非常熟悉的函数实例，引导学生一步一步探究函数的和差积商的导数的求导法则，学生的思维在逐步向深度和广度扩散，通过有目的的猜想与验证，激发了学生的学习兴趣，又让学生体会了数学结论的发现过程——先猜再证，培养学生发现问题，解决问题的能力，在探究的过程中，蕴含着从特殊到一般的归纳推理，由此及彼的类比推理，学生的学科素养在潜移默化中得到培养.这节课表面看起来主要是在进行法则的推理论证，缺少法则的应用，但其实在四个求导法则的演变过程中，求导法则的运用一直穿插在其中.可以看出，数学核心素养中的直观想象，数学抽象，逻辑推理和数学运算等多个部分渗透于整节课中，这样的课堂可能更受学生的喜爱，更符合新课程的标准，也是核心素养教学所倡导的.