“翻棋”
毛传林
摘要:众所周知,所有的整数能够被分成奇数和偶数两大类,我们也经常选0作为偶整数这一类的代表,选1作为奇整数这一类的代表。我们对自然界中存在的各种物体,看到的各种现象都在进行着分类,并选出一类中的某个典型代表作为这一类的标准型。
关键词:翻棋 数学 转化 分类 标准型
整数分为奇数和偶数,二次曲线分为椭圆和双曲线。给定一个二次曲线方程,怎么判断其是椭圆还是双曲线?常见的做法是将曲线方程化为标准型,然后再加以判别。实际上,此方程中蕴涵着转化、分类,并从每一个类中选出一种最为简单、最能够反映性质的元素,作为这一类元素代表的逻辑过程。此外,每一个类中的元素,由于都能够转化为标准型元素,所以同一类中的元素之间实际上是可以相互转化的。本文以“翻棋”游戏作为研究对象,简单浅析说明转化、分类、确定标准型这一深刻的数学思想。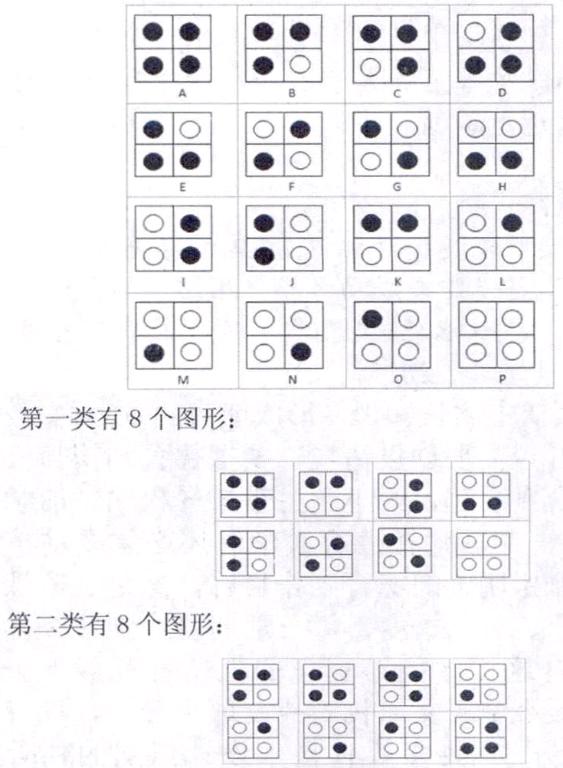
“翻棋”游戏常常被描述如下:在3× 3方格中有9颗棋子(棋子的正面是黑色,反面是白色)。每次任选一行或者一列,把所选行或列的全部棋子正反面翻转叫做一次T操作。请问:能否经过有限次T操作,将某个图形下的棋子全都变成黑色朝上?
一、1× 1方格和2× 2方格
3× 3方格里面9个棋子,每个棋子正反面又分别有黑白两种颜色,这样对应的图形将会产生29(=512)种可能情况,似乎太多了点。我们先来考虑1× 1方格和方格2× 2方格两种较为简单的情况吧。
很容易看到1× 1方格只有一个格子,里面棋子如果是正面黑色朝上,那么不用操作,或者说经过0次T操作,就把全部棋子变成黑色朝上了;如果是反面白色朝上,那么只需要经过1次T操作,就可以把全部棋子变成黑色。所以,可以得到结论:对于1×× 方格,不论棋子怎么摆放,我们都可以经过有限次T操作,将棋子全部变为黑色。
現在,来讨论2× 2方格的情况。在2× 2方格中放上棋子,将会产生16种可能情况,不算太多,我们可以把他们全部画出来,如下:
为了方便叙述,我们给上述16种情况给出ABCD……的编号,并写在图形下方。注意到每经过一次T操作,从一个旧的图形出发,我们可以得到一个新的图形,如选图形A的第2行进行T操作,我们会得到图形K;当然,选图形K的第2行进行T操作,我们会重新得到图形A。这使得我们意识到,假如两个图形可以经过有限次T操作相互转化,那么他们中只要有一个最终可以通过有限次T操作变成全部黑面朝上,则另外一个图形也可以通过有限次T操作变成全部黑面朝上了。这种转化,驱使我们想知道,看哪些图形之间可以相互转化,而哪些图形之间不能相互转化。我们把可以相互转化的图形看作是一类的。这样,问题来了:所有图形能够分成多少类呢?
命题1:我们规定,如果两个图形,可以经过有限次T操作相互转化,那么这两个图形被说成是同为T类的;否则,被说成不是同为T类的。
问题:2× 2方格下棋子的图形,经过有限次T操作,可以分为多少个不同的T类?
在2× 2方格的情况下,我们可以将全部16种图形分成下述两类。请读者自行验证,上述同一类的图形如何通过T操作相互转化。
由上述分类可以看出,对于2× 2方格,如果正面黑色朝上的棋子个数是偶数的时候,相应的图形可以经过是可以经过有限次T操作变成图形A,也就是全部黑色朝上的;否则,正面黑色朝上的棋子个数是奇数个的时候,相应的图形是不可能经过有限次T操作变成图形A的,但是我们发现它们总可以变成图形B。实际上,这时,我们就把图形A当成了第一类中所有图形的代表,图形B当成了第二类中所有图形的代表,图形A和图形B也被称为标准型。
二、3× 3方格
3× 3方格中棋子对应的图形的情况有29(=512)种之多,不可能像2× 2方格时那样一一罗列出来,该怎么办呢?我们发现,在处理2× 2方格时,通过图形间的转化,分类,并确定标准型的想法还是可以使用的。 最后,我们得到的图形,第1行3个格子和第1列3个格子里面的棋子一定都是黑面朝上。这样的一个图形我们称之为标准型。综合上面的分析,我们可以得到下述命题:
命题2:令X是一个3× 3方格棋子的图形,那么可以经过有限次T操作,将图形X变成一个第1行3个格子和第1列3个格子里面的棋子都是黑面朝上的标准型。
对于一个3× 3方格下棋子的图形,它可以转变到两个或者多个标准型吗?下面的命题告诉我们,这是不可能的,它只可能转变成一个标准型。
命题3:令X是一个3× 3格下棋子的图形,经过有限次T操作将X转化为标准形,那么X只有唯一的一个标准形。 证明:设图形X可以经过有限次T操作化为标准型Y,也可以化为标准型Z。假设Y和Z在某个格子里的
棋子颜色不一样。不妨,在这个格子里,Y图形的棋子是黑色,Z图形的棋子是白色。可以看到,需要对Z图形里,这个白色棋子所在的行或者列,一共进行奇数次T操作,才能将这个棋子的颜色变成黑色。但是,这将导致,Z图形中,和这个白色棋子位于同一行或同一列的第1个棋子的颜色变为白色。 所以图形Y和Z是不能通过有限次T操作相互转化的。这与他们都可以通过X经过有限次T操作转化而来矛盾。我们得到结论,Y和Z必须完全相同,也就是X只有唯一的一个标准型。
三、结论
在各种数学理论或者专著中常用的术语“等价关系”和“等价类”,大众读者往往只能记住这两个术语的数学描述,而不知其到底为什么要给出这样的描述,于是就有了数学抽象、深奥,但却不切实际的感觉。实际上,所谓“等价关系”就是对元素可以相互转化的抽象描述,“等价类”也就是在讲可以相互转化的所有元素被视为一类。所以,数学理论中,一般只要出现这两个术语的地方,对应的就是在对研究对象进行分类。
通过“翻棋”这一简单而有趣的游戏,在游戏过程中,首先对图形变化有了朴素的感性认识。然后,利用分类的基本方法论,能够使学生在数学上对怎样分类,如何分类,怎么确定标准型,有个理性认识,从而慢慢理解“等价关系”和“等价类”内涵,最终掌握分类的基本方法论。
参考文献:
[1]张远南.使人聪明的数学智力游戏[M].上海科学普及出版社,1993.
[2]Brina Bolt著.黄启明译.数学乐园[M].浙江科学技术出版社,1997.
——如何培养学生的创新思维

