基于二阶滑模算法的双电机后驱车辆差速系统设计

华星淇，何 锋

（贵州大学机械工程学院，贵州 贵阳550025）

1 引言

随着经济快速发展以及人们对环境问题越来越视重视，使得人们对电动汽车的需求逐渐旺盛［1］。但电动汽车的安全性令人担忧，尤其是侧向稳定性，它是影响电动汽车安全性的主要因素之一［2］，已经成为汽车动力学领域的热门课题。高速转向时，车辆内外轮行驶路径不同，微小的速度偏差将会引起车辆侧向不稳定问题，甚至引起交通事故。而差速系统利用对驱动力的分配，确保转向时内外轮速跟随路径同步变化，从而实现了车辆的稳定转向［3］。

在差速系统设计过程中，为了提升车辆侧向稳定性，通常选取横摆角速度和质心侧偏角共同对车辆进行控制［4］。因此，这是一个多目标控制问题。此外，普遍认可的是滑模控制应用在多目标控制上有很多优点，例如，它能够克服系统的不确定性，对外界噪声干扰和参数摄动具有很强的鲁棒性，尤其是对非线性系统的控制具有良好的控制效果［5］。文献［6］设计了基于滑模控制器的直接横摆力矩控制，结合主动转向系统，有效提升了车辆在高速转向时的侧向稳定性，并且在对抗外界干扰时具有鲁棒性。但是，它仍然有不足之处。例如，滑模控制算法中含有符号函数，使得系统在运行过程中多次穿过切换面，容易引起严重的系统抖振。按照文献［7］的描述，这些抖振会严重影响系统控制精度，甚至引起控制系统崩溃。

为了解决上述问题，本研究拟采用二阶滑模算法，通过导数的定义将穿越滑模面的非连续控制函数变为连续控制函数，以减少穿越滑模面的次数，进而降低系统抖振。首先，建立车辆二自由度模型，获得控制变量与车辆运动状态关系。其次，建立7自由度车辆模型，解析横摆力矩与车辆动力学行为关系。在此基础上，根据所建模型和滑模理论推导出二阶滑模控制算法，并基于双电机后驱车辆进行差速系统的设计。最后，设计双移线工况，利用计算机仿真软件Carsim与Simulink联合仿真进行验证。

2 模型搭建

2.1 车辆2自由度模型

为了简化控制器的设计，假设车辆质心处的纵向速度为常数，且车轮侧偏角足够小，则可以建立如图1所示的线性2自由度车辆模型。2自由度模型包括车辆的侧向运动与横摆运动两个自由度，从理论上描述了车辆转向角、质心侧偏角和横摆角速度的关系。此外，考虑车辆轮胎侧向力对车辆运动的影响［8］，利用牛顿第二定律，二自由度模型可以用平衡方程表述为：

图1 车辆线性二自由度模型Fig.1 Linear 2-DOF Model for Vehicle

式中：m—车辆质量，vx—车辆纵向速度，δ—前轮转角，β—车辆质心侧偏角，γ—车辆横摆角速度，Cf Cr—前轮轮胎侧偏刚度和后轮轮胎侧偏刚度，lf lr—车辆质心到前后轴的距离，Iz—车辆横摆转动惯量。

考虑到当车辆在稳定状态下运行时，车辆质心侧偏角和横摆角速度为常数。则质心侧偏角速度β˙和横摆角加速度γ˙恒为0，则式（1）化为：

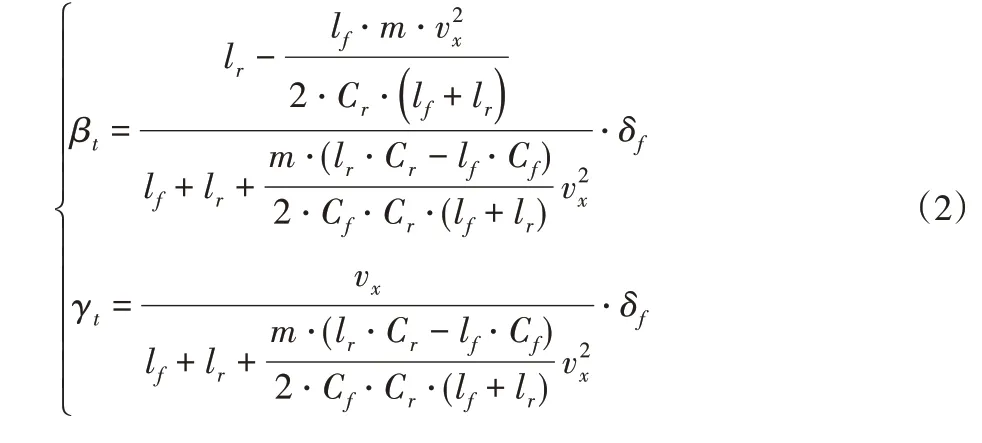
同时，为了防止车辆侧向力在大的侧向加速度下达到极限，考虑轮胎道路附着系数μ，对横摆角速度和质心侧偏角设置如下边界［9］。

综上所述，可以得到理想的质心侧偏角和横摆角速度表达式，

2.2 七自由度车辆模型

七自由度车辆模型是为了分析车辆运动而建立的。如图2所示，忽略俯仰、侧倾运动，建立了一个包括纵向运动、侧向运动、横摆运动以及四个车轮转动的7自由度非线性车辆模型。相关的方程表示如下：

图2 七自由度车辆模型Fig.2 7-DOF Vehicle Model

纵向运动方程为：

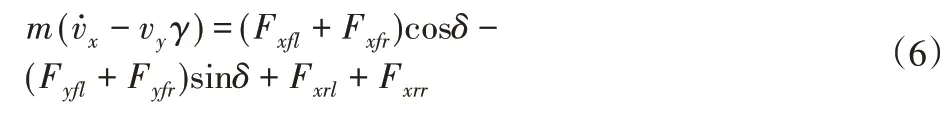
侧向运动方程为：

横摆运动方程为：

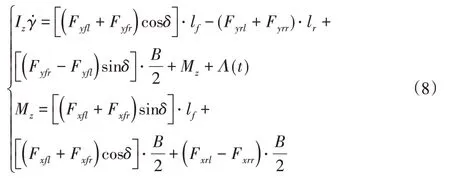
式中：Fxij和Fyij—车轮的纵向力和侧向力，B—轮距，Mz—横摆力矩，Λ(t)—一个有界块扰动，包含系统的不确定性和外部干扰，它的值由系统误差决定。

3 控制系统设计

设计如图3所示的双层控制器控制结构，其中，上层控制器用以计算总的修正力矩，下层控制器根据总修正力矩以及车轮垂直载荷对驱动轮驱动力矩进行重新分配。

图3 控制系统结构图Fig.3 Structure Diagram of Control System

3.1 上层控制器

本节中，将会设计一种二阶滑模控制器，用以降低系统抖振并提高控制精度。

二阶滑模控制是目前应用最广泛的高阶滑模控制方法［10］，因为它的控制器结构简单且所需要的信息不多。根据Levant的理论［11］，二阶滑模是将控制输入x的导数˙看作新的控制变量，设计不连续的控制使得滑模变量使得s→0，并保持二阶滑模动态，即s=s˙=0。而控制输入x是通过对x˙的积分得到的，故是连续的，从而抑制了系统的抖振。

此外，有限时间到达的二阶滑模在具有零阶保持器的离散控制下，它的精度是采样时间的二阶无穷小，即O(τ2)，由于采样步长τ往往小于1，所以它比传统滑模具有更高的控制精度。

在设计滑模控制器过程中，首先应建立滑模系统的切换面［12］，因此，考虑使横摆角速度和质心侧偏角误差最小的原则，设计切换面为：

式中：ξ＞0—权重系数，反映了质心侧偏角偏差的比例。S的导数为：

则横摆运动方程（8）可重新表述为：

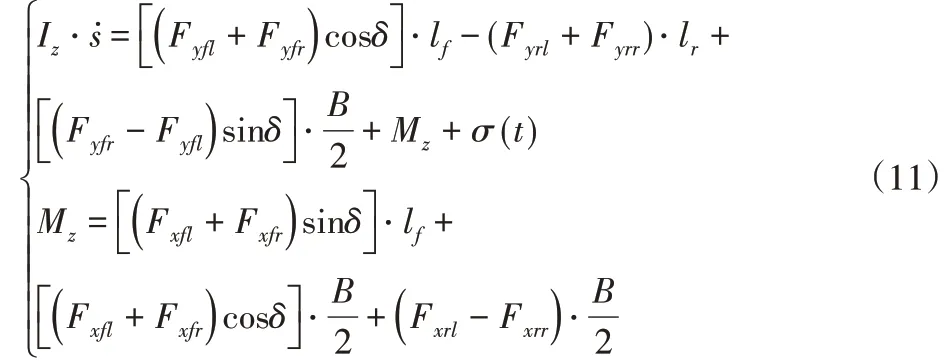
对s进行二次积分可得：

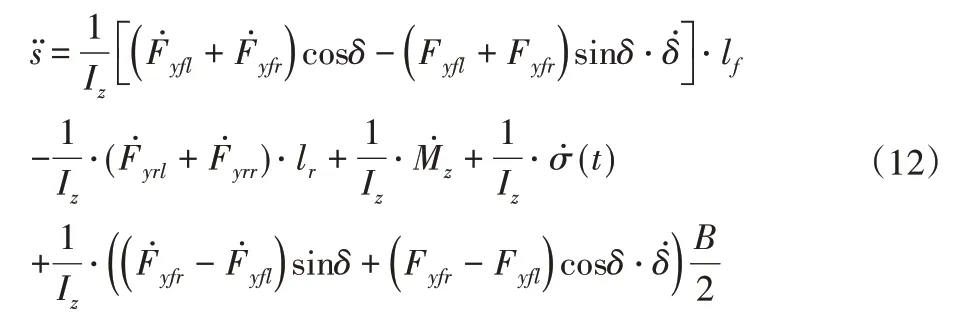
将公式（12）写成如下形式：

式中：φ(t,γ)可以表达为：

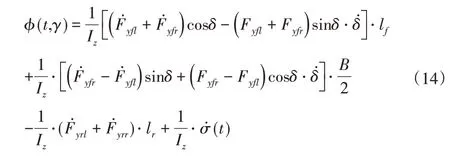
在实际应用中Fyij(i=f,r;j=l,r)总是有界的，且(i=f,r;j=l,r)总是变化缓慢，所以，式（14）也总是有界的，至少局部有界。因此，总可以找到一个使得 ||φ(t,γ)≤。

采用等速趋近律，则可以设计如下控制器：

式中：˙=-εsgn(s)-k·s，则式（4）可以重新描述为：

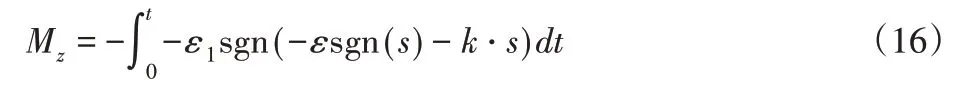
（1）当s＞0时，左侧恒有：

右侧恒有：

所以此时，可得到：

（2）当s＜0时，左侧恒有：

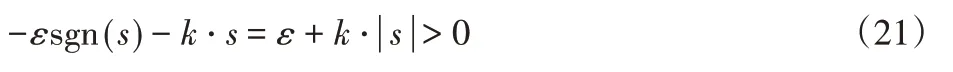
右侧有：

因此，二阶滑模控制器为：

3.2 下层控制器设计

下层控制器的核心是力矩分配策略设计，研究所用的双电机电子差速车辆的结构如图4所示，它比单发动机具有更多优势。比如取消了分动器、液力变矩器等传统机构，降低了整车质量。此外，每个驱动轮可独立控制，使得力矩的控制范围更大［14］。

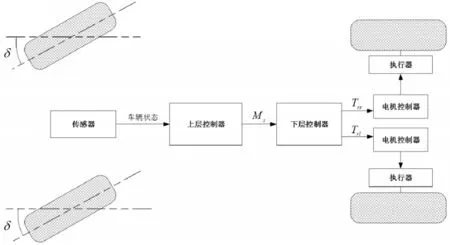
图4 双电机后驱车辆结构示意图Fig.4 Schematic Diagram of Dual Motor Rear Drive Vehicle

首先，车轮纵向力和驱动力矩的关系可以表达如下：

其次，从图2的7自由度车辆模型中分析可得：

式中：Fzij和Tij—车轮的垂直载荷以及车轮的驱动力矩。

4 实验验证

为了验证3.1节提出的驾驶员模型，利用Simulink和carsim进行双移线工况的联合仿真。仿真参数见表1。

表1 仿真参数Tab.1 Simulation Parameters

双移线工况是模拟汽车避障或超车时的行驶工况［15］，在汽车性能测试中经常使用。由于存在两个方向相反的紧急弯道，可以通过道路变化验证所设计差速系统的有效性。双移线仿真实验的道路轨迹参数如图5所示。

图5 双移线测试路径参数Fig.5 Double Lane Change Path Parameters

在图5中，E点为车辆驾驶入口，S0=50m，S1=15m，S2=30m，S3=S4=25m，S5=15m，S6=50m，变道宽度S7=3.5m。在carsim软件中建立双移线仿真实验的道路轨迹，如图6所示。仿真结果如下图所示：

图6 Carsim中建立的双移线路径示意图Fig.6 Schematic Diagram of Double Lane Change Established in Carsim

从图7路径分析可知，利用一阶滑模控制器和二阶滑模控制器的仿真结果差别很小，即首先证明了二阶滑模控制器的有效性，保证了车辆按期望路径行驶。

图7 路径仿真结果Fig.7 Path Simulation Results

从图8质心侧偏角仿真结果可以得出，二阶滑模控制器在时间3.5s、4.5s、6.5s、7.5s位置的结果比一阶滑模控制器的结果要小，其余时刻基本一致，这反映了二阶滑模控制器在双移线转向段路径的控制效果要优于一阶滑模控制器。

图8 质心侧偏角仿真结果Fig.8 Simulation Results of Mass Side Slip Angle

从图9横摆角速度和图10侧向加速度的对比图可以得知，使用了二阶滑模控制器的结果比一阶滑模控制器的结果更为清晰，整体振幅均有所下降，即二阶滑模控制器明显降低了一阶滑模控制器表现的抖振现象。

图9 横摆角速度仿真结果Fig.9 Simulation Results of Yaw Rate

图10 侧向加速度仿真结果Fig.10 Simulation Results of Lateral Acceleration

从图11总修正力矩的仿真结果中可以看到，二阶滑模控制器明显降低了一阶滑模控制器总修正力矩的幅值，即滑模控制器的抖振问题得到解决。

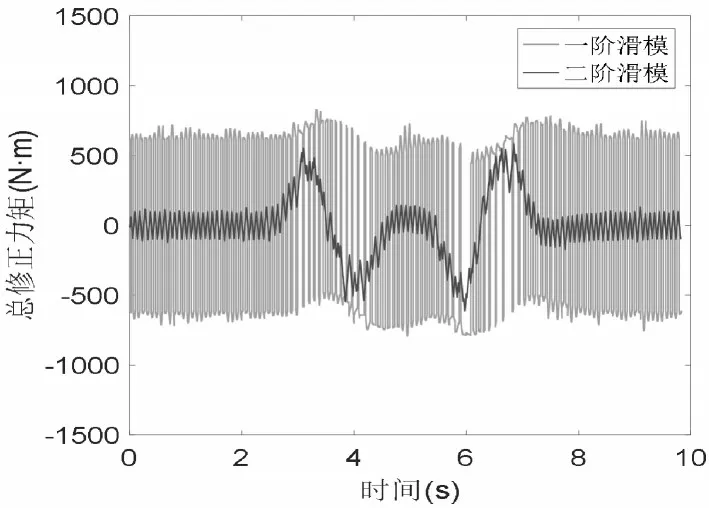
图11 总驱动力矩仿真结果Fig.11 Simulation Results of Total Driving Torque

从图12差速驱动力矩仿真结果可以得出，驱动轮力矩分配策略有效，左右轮分别承担了不同的驱动力矩分配。

图12 差速驱动力矩仿真结果Fig.12 Simulation Results of Differential Driving Torque

5 结论

在本研究中，结合质心侧偏角和横摆角速度等车辆侧向稳定性参数设计了一个双层结构控制器，使得能够实现双电机后驱车辆提升侧向稳定性的差速力矩分配。总的分配力矩在上层控制器中计算，下层控制器则利用转向时车轮垂直载荷不同将总分配力矩分配给左右驱动轮。仿真结果表明，差速系统在路径控制上利用二阶滑模算法比一阶滑模效果更好，不仅如此，基于二阶滑模算法设计的控制系统明显降低了一阶滑模出现的抖振。综上，基于二阶滑模算法设计的差速系统可以有效提升双电机后驱车辆的侧向稳定性，并能有效抑制滑模算法的抖振。