一种新型滚动集电环的设计研究
胡 扬,戴恒震
(大连理工大学机械工程学院,辽宁 大连116024)
1 引言
旋转连接器是实现两个相对旋转部件间360°无限制传输功率和信号的输电装置,广泛应用于风电、军事雷达、航空航天等领域[1]。传统滑环由于其滑动接触的特性,在工作过程中易出现摩擦磨损,严重影响了滑环的工作性能和使用寿命。而滚动集电环(滚环)使用滚动接触代替滑动接触,滚动电接触摩擦副理论上是一种纯滚动,不会产生磨损,与传统滑动集电环装置相比,滚环具有工作寿命长,性能可靠及免维护等优点,适合应用在需长时间工作,现场维护困难的场合中[2-3]。
滚环由球轴承和电传输技术演变而来。在此基础上,美国人Peter Jacobson于20世纪80年代发明了具有实用价值的滚环,并成功应用于国际空间站α驱动机构(SARJ)中。滚环相关技术已在国外发展40余年,经过不断改进和优化,其技术日趋成熟,并已投入商业使用[4-5]。国内对滚环的研究还处于摸索阶段,主要以理论分析和测试样机为主,尚未得到实际推广与应用。
滚环中的核心部件—柔性环,其状如戒指,半径小,壁厚仅0.3~0.5mm,普通加工手段难以满足;且滚环一般安装多个柔性环以提高传输功率,如何使其保持同轴、同心及共面也是一项技术难题[6]。研究人员为此提出多种改进方案,比如Jacobson等人于2004年提出了一种柔性联结器,替代内外导电环之间的柔性环,有效降低了加工难度[7]。
目前已有的改进均是关于柔性行星环的,尚未有人提出基于导电外环的改进方案。将导电外环作为柔性环,既能保持滚环原有性能,又可以有效降低加工和装配难度。针对这种滚环装置,利用材料力学、电接触理论和ANSYS软件,构建其工作寿命和接触电阻的计算模型,并结合设计实例计算,最后进行有限元仿真验证。
2 新型滚环的结构设计
新型滚环由内部导电环、凹槽滚轮、保持支架、柔性外环、悬臂柔性支撑及绝缘外壳等零件构成。柔性外环、凹槽滚轮和内部导电环组成了滚动电接触副,如图1所示。

图1 新型滚环爆炸示意图Fig.1 Explosion Diagram of the New Rolling Collecting Ring
柔性外环受径向挤压而产生弯曲预紧力,使柔性外环、凹槽滚轮及内部导电环之间紧密接触,使得导电内环转动时,带动凹槽滚轮在柔性外环及导电内环之间滚动,完成内外环之间的电传输。保持支架将滚轮隔开,限制其周向距离,防止在滚轮滚动过程中相互之间发生碰撞或运动干涉。
在滚环工作过程中,柔性外环和导电内环卡在滚轮的凹
形槽中纯滚动。若传输力矩带动内轮顺时针旋转,柔性外环保持固定,则凹槽滚轮随之逆时针自转,并绕着滚环的轴线作顺时针公转,如图2所示。

图2 柔性环运动示意图Fig.2 Motion Diagram of Rolling Collecting Ring
如图3所示,由于柔性外环在工作过程中受到挤压不断发生弯曲变形,需合适的导电通道将电流和信号从柔性外环导出。本装置采用柔性导电悬臂支撑作为导电通道,其核心为弹性支撑,不仅支撑柔性外环,还使柔性环与悬臂梁紧密接触,保证电流和信号的稳定传输。

图3 柔性外环变形示意图Fig.3 Deformation Diagram of Rolling Collecting Ring
以导电外环作为柔性环的设计方案,使滚环的加工难度下降,结构也更加紧凑可靠;同时降低了装配难度,加工成本减少。
3 疲劳寿命计算模型
3.1 弯曲应力分析模型
图3中,因柔性外环的半径R小于导电内环半径R1与滚轮直径D2之和,柔性环将受到挤压变形而产生电接触预紧力F,柔性外环的变形量为:

将预紧力F中使柔性环变形的部分以F1表示,使悬臂支撑弯曲变形的部分以F2表示。经力学分析可知,柔性外环的弯曲形变和弯曲应力由δ决定,即F1的大小与外部的柔性支撑架无关。滚环的简化力学模型,如图4所示(三滚轮为例)。

图4 滚环受力变形示意图Fig.4 Force Diagram of Rolling Collecting Ring
图4-(a)中,在F1的作用下,柔性外环产生了径向弯曲变形,如图3虚线所示。同一时刻,柔性外环的不同位置产生了不同的弯曲变形。滚环是对称结构,其受力状态在任意时刻均是对称的,可以只取一段(1/6)出来研究,如图4-(b)所示。
由材料力学的知识可知,此为三次超静定问题,可以得到圆弧GAD上的任一截面的弯矩表达式:

由卡氏第二定理,可以得到径向位移Δ与F1之间的关系表达式,其中Δ在A处取得最大值:

弯曲应力计算公式为:

式中:y—计算应力点到截面中性轴的距离,I—柔性外环的横截面对中性轴的惯性矩。

式中:w、t—柔性外环的宽度和壁厚,t近似等于2y,联系式(2),(4)和(5),得到Mmax与F1之间的关系表达式:

联系式(1)和(3),(6)可以得到最大弯曲应力与径向压缩量之间的关系表达式:

图4(c)中悬臂梁的长度为l,宽度为w1,厚度为t1,根据材料力学,可以得到悬臂梁的最大弯曲应力表达式:

利用滚环的对称性,绘制其弯曲应力分布图,如图5所示。滚环运动时,其上各点会受到周期性的弯曲应力。
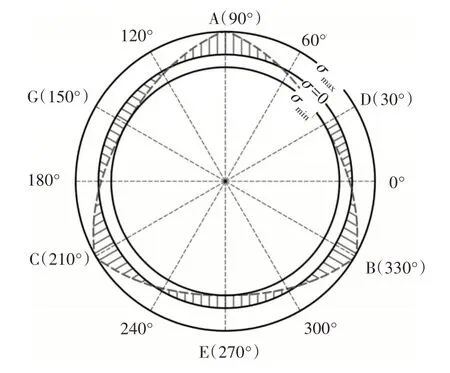
图5 滚环的整体弯曲应力示意图Fig.5 Diagram of the Bending Stress of Rolling Collecting Ring
当滚轮数量(n=2、3、4、5)增加时,柔性外环所受最大弯曲应力σmax也随之增加,其表达式,如表1所示。

表1 柔性外环的最大弯曲应力表达式Tab.1 Maximum Bending Stress Expression
3.2 工作寿命计算模型
滚环工作是纯滚动,无摩擦磨损,其主要失效形式是柔性外环的疲劳破坏,因此滚环的工作寿命取决于柔性外环的疲劳寿命。柔性外环所受的交变应力为弯曲应力,根据弯曲应力的计算公式和柔性环材料的S-N图,便可以得到柔性外环的疲劳寿命。铍青铜具有高弹性、高硬度、耐磨及高导电性等特点,是制造柔性外环的理想材料。查阅文献[8],可以得到代号为QBe2.0的铍青铜的弯曲疲劳强度与循环次数的关系。
已知柔性外环的疲劳寿命为No,滚轮的数目为n,利用滚环的运动关系,得到导电内环的额定转动次数Ni的表达式为:

由表1内的公式求出柔性外环所受的最大弯曲应力,结合S-N图和式(9),便可以得到导电内环的额定转动次数Ni。
4 接触电阻计算模型
4.1 接触电阻理论
由文献可知[9],金属导体之间实际发生机械接触的点称为接触斑点,接触斑点中实际传导电流的部分则称为导电斑点,实际接触面积Ar只是名义接触面积Aa的一小部分。承载接触面一般覆盖着污染膜,不是可靠的电流传输通道,因此导电接触面积也只是计算的实际接触面积Ar的一小部分,通常认为远小于1%。两个互相接触的粗糙表面,电流线在导电斑点附近发生收缩,使电流流过的路径增长,将产生局部附加电阻,称为收缩电阻Rs,如图6(a)所示。当电流通过导电斑点时,还会经过接触表面上的污染膜(氧化物、硫化物和反应生成物等),这种因污染物而产生的附加电阻称为膜电阻Rf。R.Holm将这些导电斑点假设为半径为a的圆形,图6(b)是单个半径为a的圆形导电斑点的收缩电阻示意图。

图6 收缩电阻形成示意图Fig.6 Schematic Diagram of Constriction Resistance
对于两个电阻率分别为ρ1和ρ2的接触元件,R.Holm给出了单个半径为a的圆形导电斑点的收缩电阻Rs的计算公式:

若ρ1=ρ2,则:

膜电阻Rf的计算公式为:

式中:σ—膜层单位面积的电阻。
单个导电斑点的接触电阻是由Rs和Rf串联而成,两者相加便得到接触电阻Rc:

假设滚环各部件之间的接触均为弹性Hertz接触,建立滚环的接触模型,如图7所示。图7(a)是柔性外环、滚轮与导电内环之间的接触,图7(b)是柔性外环与悬臂支撑之间的接触。

图7 滚环的接触模型示意图Fig.7 Diagram of Contact Model of Rolling Collecting Ring
其中a为接触面的半宽,根据弹性接触(Hertz接触理论)[10],得到接触面半宽a的表达式:
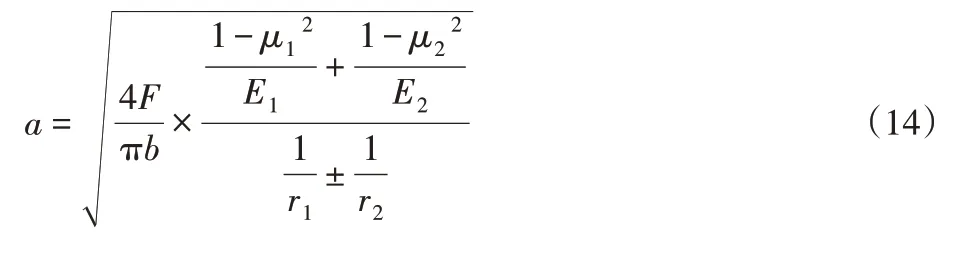
根据上式可以依次求出各个接触面的半宽a1,a2,a3。已知接触面是长为b、宽为2a的矩形,则滚环中滚轮与导电内环
之间的接触面积Ac为2ab。接触表面是不均匀的,上述得到的接触面积都是名义接触面积Aa,不是真正的实际接触面积Ar,而且获得导电斑点的面积和数目是非常困难的。因此为方便计算,本文将整个名义接触面积作为整个导电斑点,近似计算其收缩电阻,并用式(10)可推出此近似值为最小值:

矩形导电斑点的表达式根据Aichi和Tahara的研究[11]可知:

式中:当收缩形状比(b/2a)是10以上时,S—矩形收缩的面积,k—一个参数,它取决于收缩部分的宽度,当收缩部分的宽度从1增加大10mm时,它从0.36增加到1。
滚环上的接触面为防止腐蚀,一般都作镀层处理,加上滚环常应用于大电流环境,氧化膜及其它无机膜将会在高温下熔融破解,此时膜电阻便可以忽略不计,因此可以认为滚环工作时的接触电阻近似等于收缩电阻。
4.2 滚环分路电阻计算模型
滚环的导体电阻值一般很小,为简化分路总电阻计算,假设其值为零。得到滚环分路电阻示意图,如图8所示。
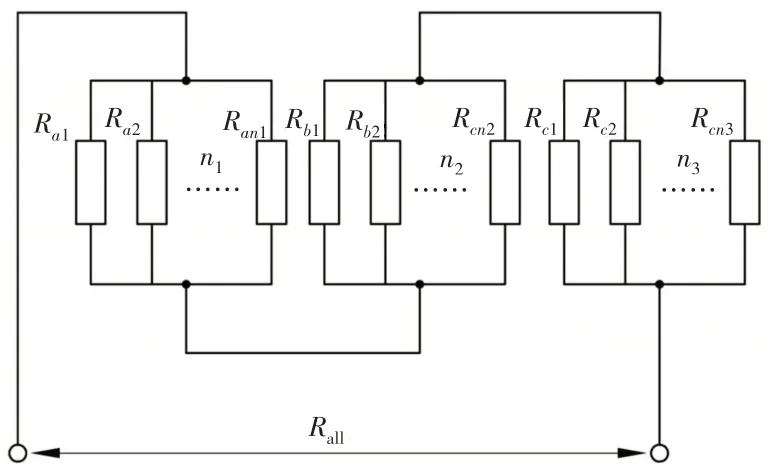
图8 滚环的分路电阻示意图Fig.8 Diagram of Distributed Resistance of the Rolling Collecting Ring
图中,Ra—悬臂支撑与柔性外环之间的接触电阻,n1—悬臂支撑的数量;Rb—柔性外环与滚轮之间的接触电阻,n2—滚轮的数量;Rc—滚轮与导电内环之间的接触电阻,n2等于n3;Rall—总接触电阻。则总接触电阻的表达式为:

5 分析与计算
5.1 滚环的工作寿命影响因素分析
滚动集电环工作寿命取决于柔性外环的最大弯曲应力值σmax。由式(7)和表1可知,σmax与柔性外环的径向压缩量σ、弹性模量E、壁厚t,数量n正相关,与R2负相关。柔性外环的材料和半径已知,因此可以排除E和R2。改变滚环零件的尺寸,柔性外环的径向压缩量δ也会随之改变。考虑到柔性外环的摩擦力矩、加工难度和形变难度,结合资料,给出的δ取值范围为[0.2,0.8]mm,t的取值范围为[0.3,0.6]mm,以δ和t为自变量,最大弯曲应力σmax因变量,示意图,如图9所示。

图9 最大弯曲应力的影响因素示意图Fig.9 Diagram of the Factors Affecting the Maximum Bending Stress σmax
由图9和表1,可以得出:随着柔性外环径向压缩量δ、壁厚t和滚轮数量n的增加,σmax增加,疲劳寿命降低。
5.2 滚环的接触电阻的影响因素
由式(14)和(16)推导出滚环的单个接触电阻表达式为:

结合式(17)和(18),可以得出结论:随着预紧力F和滚轮数量n增加,接触电阻降低。
5.3 实例计算
表2和表3给出了滚环各零件的材料参数和零件尺寸。

表2 材料参数Tab.2 The Material Parameter

表3 新型滚动集电环设计实例数据Tab.3 The Design Data of New Rolling Collecting Ring
已知某滚环的设计工作寿命Ni为107转,接触电阻Rs为100uΩ。结合上文及式(9)和(17),计算得出滚动集电环(n=3)的疲劳寿命为4.86×107转,总电阻Rall为15.8uΩ。根据以上计算结果,可知新型滚环的工作寿命和接触电阻均达到了设计标准与使用要求。
6 弯曲应力仿真分析
根据表2和表3中的滚环设计参数,应用ANSYS仿真软件对滚环所受应力进行仿真校核,除去保持支架、导电接口等零件以简化有限元网格模型:
(1)划分网格时,单元尺寸限制为1.0mm,整体采用自适应网格划分技术,接触部分采用局部尺寸控制,最后得到16735个单元。单元平均质量为0.76,大于0.7,满足使用要求;
(2)悬臂支撑—柔性外环接触、柔性外环—滚轮接触均是凸面为接触面,凹面或平面为目标面。因此接触形式均采用rough面对面接触,自动非对称接触(Asymmetric)行为,界面处理中offset值为0;
(3)用位移(Displacement)方式对滚轮施加径向方向0.5mm的压缩量,悬臂支撑和柔性外环均只有径向自由度,悬臂支撑的底座为固定约束;
(4)后处理,将等效应力(Equivalent stress)作为输出结果。仿真结果,如图10所示。

图10 滚环弯曲应力仿真结果Fig.10 Bending Stress Simulation Results of Rolling Collecting Ring
如图10(a)所示,弯曲应力最大值σmax出现在滚轮与柔性外环的接触处,此时柔性外环外表面受拉,内表面受压,σmax为151.6Mpa;在外表面受压,内表面受拉的环段,σmax位于中点处,为84.2Mpa;如图10(b)所示,悬臂支撑的弯曲应力最大值达到59.6Mpa,位于悬臂支撑固定处。由式(7)和(8)计算出柔性外环弯曲应力值最大值为158.3Mpa,悬臂支撑的最大弯曲应力值为55.67Mpa,与仿真计算的结果误差在5%左右。
将柔性外环边缘上沿环一周的应力数据提取出来,并与式(2)和式(4)计算的数据进行对比以进一步研究,如图11所示,柔性外环沿环一周的弯曲应力值呈现出显著的周期变化,可知周期长度与两相邻滚轮之间的弧长相等,周期数与滚轮数量一样,这是因为滚环是旋转对称结构,受力状态也呈对称性;弯曲应力的变化曲线有两个峰顶,较大的峰顶对应滚轮与柔性外环的接触点,较小的峰顶对应两相邻滚轮之间的弧段中点;两峰值之间的零点,则代表着柔性外环表面应力状态开始发生由受拉向受压或由受压向受拉的转变。

图11 柔性外环的弯曲应力理论计算与仿真结果对比Fig.11 Comparison of Calculation and Simulation
由理论计算与有限元仿真对比可知,理论计算的应力变化曲线与仿真计算的结果具有高度的一致性,周期基本相同,峰值相对误差在5%左右。相对误差主要源于两个方面:一是因为理论计算中公式(6)中的y取的是近似值;二则是受限于有限元仿真的计算精度。为使研究更加准确,后续可以引入修正系数加以修正。
7 结论
通过对一种新型的滚动集电环的结构设计和理论研究,并结合仿真分析,得到如下结论:
(1)提出了一种新型滚环的设计方案,给出了详尽的结构介绍,并分析了设计的可行性;(2)滚环中柔性外环的弯曲应力影响了滚环的疲劳寿命和接触电阻,壁厚和压缩量越大,弯曲应力和接触面积越大,接触电阻就越小,可通过的电流也越大;弯曲应力越大,滚环的疲劳寿命就越短。此外,随着滚轮数量的增加,弯曲应力增大,接触电阻变小,疲劳寿命变短;(3)建立了滚环的弯曲应力和接触电阻计算模型,能够为滚环的参数设计提供重要参考;(4)经过理论研究及仿真验证,证明了用外环作为柔性环的设计思路是合理的,实例设计数据(结构尺寸、材料、径向压缩量)是可靠的,保证了滚环运动稳定及性能达标。

