纵横向运动耦合时车辆状态估计算法研究

周兴林，袁琛琦，盛中华

（武汉科技大学汽车与交通工程学院，湖北 武汉430065）

1 引言

随着车辆底盘稳定性电控系统的不断发展，车辆行驶状态信息的测量与获取显得尤为重要。车辆的主动安全性能可以通过系统识别运动过程中的动力学状态和参数来调整相应的控制策略而得以提高。

作为车辆状态估计的基本方法，经典卡尔曼滤波估计方法［1］在车辆状态参数估计的问题上应用广泛，但是该方法的应用针对线性系统。而后为了解决非线性系统的状态参数估计问题，在经典的线性卡尔曼滤波基础上扩展卡尔曼滤波（extended kalman filter，EKF）估计算法被提出，它通过对非线性函数进行线性化来消除高阶分量。文献［2］建立了整车动力学模型，并应用卡尔曼滤波观测器对汽车的质心侧偏角和横摆角速度进行了估计。文献［3-4］相继应用扩展卡尔曼滤波算法在车辆状态参数估计领域做出了突出贡献，但以上研究都是从纵向、侧向和垂向三个层面独立展开，而在实际行驶状态下，车辆的各项运动响应存在耦合作用的特征。文献［5］较早针对车辆纵横向动力学耦合问题和轮胎力耦合问题进行了研究，然而，目前我国对于车辆耦合动力学控制的研究还较少。

另一方面，国内外对车辆状态参数的估计大都针对开环系统，车辆的操纵性评价是十分复杂的问题，研究驾驶员在环仿真系统更接近车辆在实际行车条件下的情况，实用价值更高［6］。文献［7］对驾驶员转向特性的分类和在线辨识进行了实验研究。20世纪中期以来，多种不同种类的驾驶员模型被提出，预瞄控制方式相对于其它控制方式而言，更符合实际驾驶经验，能够获得更好的期望路径跟踪效果，且能够体现驾驶员实际操控车辆时的预瞄作用［8］。因此，本文基于预瞄最优曲率驾驶员模型，建立驾驶员-车辆闭环仿真系统，并结合扩展卡尔曼滤波理论对车辆的纵向速度、横向速度和横摆角速度进行测量。

2 车辆动力学模型

2.1 车辆纵横向动力学耦合模型

结合车辆纵向受力简图和车辆单轨模型横向受力俯视图，得到车辆纵横向受力俯视图［9］，如图1所示，oxy为固定于车身的车辆坐标系，车辆重心c.g.所在点o为坐标原点，x坐标轴沿车辆纵轴方向，y轴垂直于车辆纵轴方向，OXY为一个固定于地面的惯性坐标系。

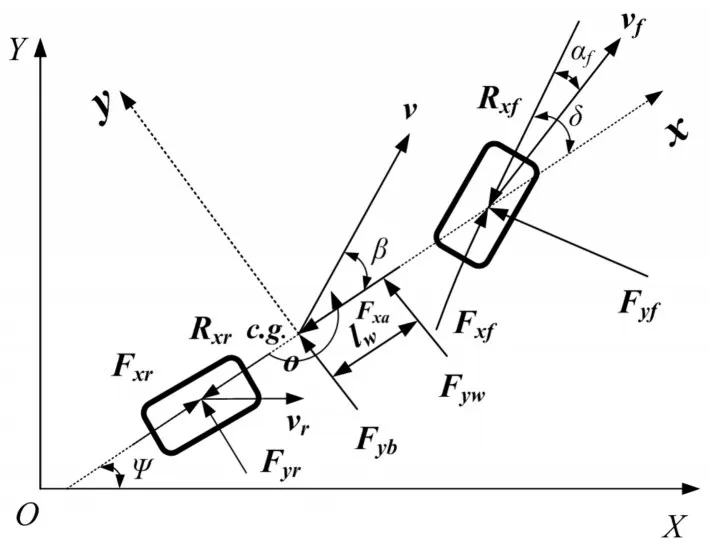
图1 车辆纵横向受力俯视图Fig.1 Top View of the Longitudinal and Lateral Forces of the Vehicle

根据牛顿运动定律，作用在车辆上的外力之和等于线动量变化率；作用在车辆上的外力矩之和等于角动量变化率。所以：

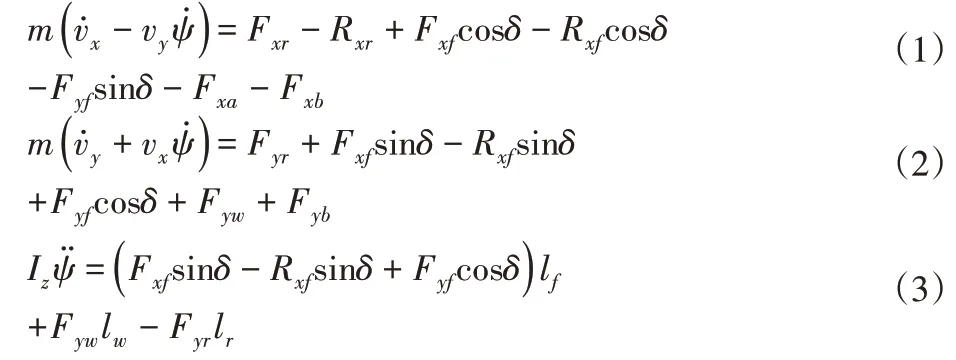
假设路面没有侧倾和俯仰，车辆不受横向滚动阻力的影响，且相对风速在纵向和横向上为零，假设δ较小，前、后轮的附着率相等，则简化后的模型公式为：

式中：vx、vy、车辆的纵向车速、侧向车速和横摆角速度；m、Iz—车辆质量和绕z轴转动时的转动惯量；a、b、k1、k2—质心到前轮的距离、质心到后轮的距离、前轮轮胎的侧偏刚度和后轮轮胎的侧偏刚度；g、fR、cx/cz—重力加速度、滚动阻力系数和比例系数；Fyw、Fyb、Fxf、Fxr、Fyf、Fyr、Ryf、Ryr、δf—侧向风力、重力沿侧向分量、地面作用在前轮上的纵向力、地面作用在后轮上的纵向力、地面作用在前轮上的横向力、地面作用在后轮上的横向力、地面作用在前轮上的滚动阻力、地面作用在后轮上的滚动阻力和前轮转向角。

2.2 轮胎模型的选择

采用Dugoff轮胎模型能够用于纵滑侧偏联合工况下的纵向力和侧向力的求解，忽略回正力矩的作用，Dugoff轮胎模型中的轮胎牵引力Fxi和轮胎侧向力Fyi可表示为：

滑移率在制动和驱动下计算公式：

车辆的垂直载荷计算公式：

式中：λ—轮胎动态参数；μ—名义路面附着系数；εr—路面附着缩减系数；cs和cα—轮胎的纵向刚度和侧向刚度；Fzi—轮胎垂向载荷；sij—纵向滑移率；i、j—轮胎位置，i—前轮或后轮，j—左轮或右轮；hg—质心高度；ax和ay—纵向加速度和侧向加速度；l—轮距；bf和br—前轮轮距和后轮轮距。

2.3 基于加速度反馈的预瞄最优曲率驾驶员模型

建立一个能反映车辆各种行驶工况的驾驶员模型是闭环控制系统中的一个关键问题。大角度单点预瞄最优曲率模型，如图2所示。经过T时间：y(t+T)=y(t)+Ty˙(t)+0.5T2y¨(t)，根据“最小误差原则”，驾驶员选择最优轨迹曲率1R*（R*为最优转弯半径），车辆在经过预瞄距离ld之后，横向位置y（t+T）与预期轨迹f（t+T）接近一致［10］。

图2 大角度单点预瞄最优曲率模型Fig.2 Large Angle Single Point Preview Optimal Curvature Model

根据离心运动状态以及最小误差轨迹跟踪原则，得到最优横向加速度：

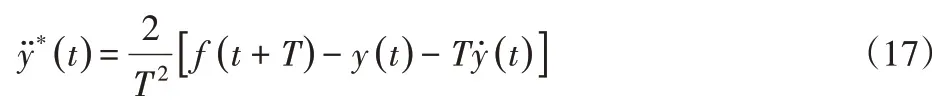
最优曲率为：

在实际道路上行驶时，Gay—车辆的横向加速度对方向盘转角的稳态增益，y¨*（t）—最优横向加速度，达到最优横向加速度应该施加的理想方向盘转角为：

对最优方向盘转角进行修正来计算实际的方向盘转角，即：

式中：δ0—考虑驾驶员生理限制后的方向盘转角，1+ths和—车辆转向盘惯性滞后环节和驾驶员神经系统反应滞后环节，th和td—转向盘惯性滞后时间常数和神经系统反应滞后时间常数。运用δ0进行方向控制时，车辆实际和理想侧向加速度之间存在偏差，此时对转向盘转角进行修正，修正量为：

式中：Δδ—车轮转角增量；δ0和修正量Δδ的和等于驾驶员模型最后决策出的方向盘转角δ。

基于加速度反馈的预瞄最优曲率驾驶员模型图，f（t+T）—预瞄时间为T的道路输入，道路输入结合侧向位移y（t）和实际侧向速度y˙（t）两个反馈信号可以得到理想的侧向加速度，经过校正环节、神经系统反应滞后和转向盘惯性滞后环节获得实际的方向盘转角作为车辆模型输入，如图3所示。

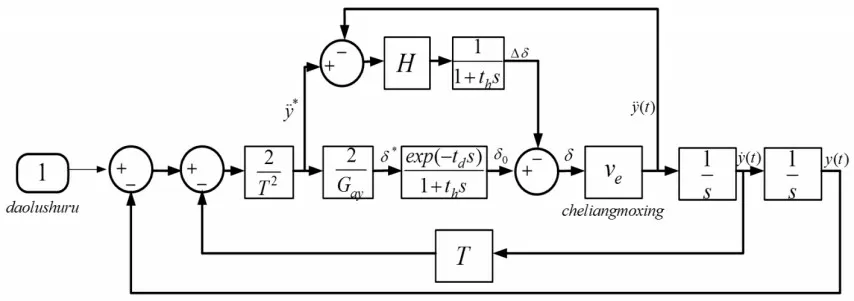
图3 基于加速度反馈的预瞄最优曲率驾驶员模型Fig.3 Pre-pumped Optimal Curvature Driver Model Based on Acceleration Feedback

为实现车辆在复杂工况下纵横向运动耦合时车辆的状态参数估计，在车辆动力学仿真软件MATLAB/Simulink环境下建立驾驶员-车辆闭环整车系统，整车系统包括车身模型和轮胎模型。其中车身模型由纵向和横向运动耦合模块组成，轮胎模型由侧偏角模块、车轮旋转运动模块、滑移率模块等模块组成。

3 基于扩展卡尔曼滤波的车辆状态估计

扩展卡尔曼滤波（EKF）是非线性系统的一种无偏最小方差估计方法。非线性系统的状态空间方程可表示为：

状态方程：

观测方程：

而在实际应用中，由于测量噪声vk和过程噪声wk不能在每个时刻以特定步长确定，所以非线性系统可以近似表示为：

状态方程：

测量方程：

扩展卡尔曼滤波估计方程推导公式如下：

初始化滤波器：

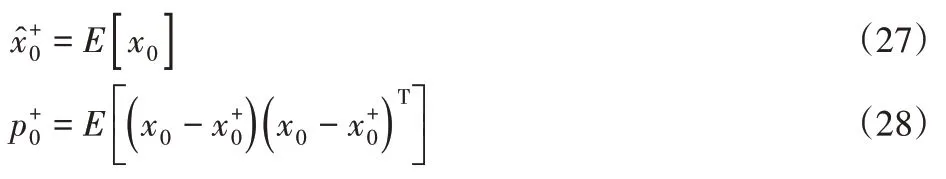
雅克比矩阵：

算法可以分为预测和校正两个阶段：

状态估计和估计误差协方差的时间更新方程（预测）为：

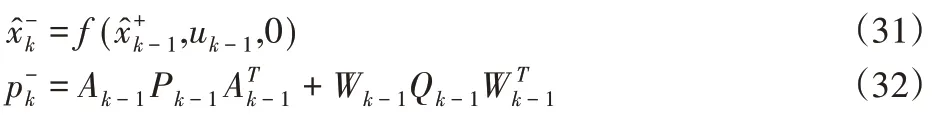
状态估计的测量更新和估计误差协方差的更新（校正）为：

Kk为卡尔曼滤波器增益，选择车辆的纵向速度、横向速度和横摆角速度作为估计器的状态变量。

状态方程表达式：

观测方程表达式：

式中：x（t）、u（t）、w（t）和v（t）—状态变量、控制变量、过程噪声和测量噪声，噪声为相互独立的高斯白噪声；Qk和Rk—w（t）和v（t）的协方差矩阵。

根据上述分析，在MATLAB/Simulink中建立如图4所示的车辆状态参数估计模型。

图4 车辆状态参数估计模型Fig.4 Vehicle State Parameter Estimation Model

4 仿真实验验证

在Matlab/Simulink软件下对所提算法进行仿真验证，所采用的车辆主要参数为m=2100kg，车轮半径R=0.31m，绕z轴的转动惯量Iz=2549kg·m2，轮胎转动惯量Iw=2.1kg·m2，前轴到质心的距离a=1.256m，后轴到质心的距离b=1.368m，质心高度hg=0.7m，空气阻力系数C=0.34，滚动阻力系数fR=0.02，控制校正增益C0=0.2282，稳态增益Gay=4.3821。仿真中，路面附着系数设为0.5，预瞄时间T和驾驶员模型参数在仿真过程中被多次调整，在纵向车速为30m/s时，预瞄时间T为0.3s。估计器协方差p0=eye（3）*1，过程噪声协方差Q=eye（3）*0.00001，测量噪声协方差R=eye（3）*100000，估算初值赋值x1=（30，0，0）。为模拟汽车的蛇形路径行驶工况，按照穿杆试验的要求，设定相应频率和振幅的正弦道路作为系统输入。

图5中估计结果存在一定的误差，误差主要集中在波峰和波谷处，但估计值与仿真值的变化趋势具有较高的吻合度，估计值稳定性较好且最大误差不超过5%，结果表明，基于扩展卡尔曼滤波的估计模型可以更好地估计蛇形行驶条件下车辆的行驶状态。在蛇形工况开始时，车辆和驾驶员存在响应滞后，而道路突然过渡到正弦形式，此时车辆行驶轨迹与预期轨迹有较大的差异，随着车速趋于稳定，误差也越变越小。

图5 蛇形工况下车辆的行驶状态Fig.5 Driving State of the Vehicle Under Serpentine Conditions

导致误差的原因为加速度方向变化对模型精度有影响，而在纵横向耦合运动条件下，车辆轮胎垂直载荷的变化也受诸多因素影响，为使问题简化载荷分配计算并不精确；另一方面，并未考虑车身的俯仰和侧倾运动。

5 结论

本文基于纵向和横向运动耦合模型，建立了驾驶员-车辆闭环仿真系统，应用扩展卡尔曼滤波技术对车辆的行驶状态参数进行了估计。在数据处理软件MATLAB/Simulink下，得到如下研究结论：

（1）驾驶员-车辆闭环仿真模型考虑了车辆纵横向耦合运动作用特征，将道路模型输入转换为车辆前轮转角作为闭环模型的初始输入，对研究“人-车”闭环控制动力学仿真具有重要意义。

（2）通过对比估计模型结果和车辆动力学模型的仿真结果，表明该算法可以较准确地估计车辆在纵横向耦合运动条件下的状态变量，可以准确地反映车辆实际状态的发展趋势。