一种仿真数据驱动的小型无人机旋翼优化设计框架
郝佳瑞,吕利叶,孙 伟,宋学官
(大连理工大学机械工程学院,辽宁 大连116024)
1 引言
无人机应用日益广泛,故提升其的续航时间和负载能力具有重要工程意义。目前,计算流体力学(Computational Fluid Dynamics,CFD)被广泛应用于无人机旋翼优化问题的仿真计算中。文献[1]基于CFD对不同外形的无人机旋翼在悬停状态下的推力进行了对比,结论是弧型的旋翼投影形状可以得到更大的推力。文献[2]结合CFD仿真和遗传算法(Genetic Algorithm,GA)确定了无人机叶片的弦长和安装角的最佳分布。文献[3]提出了CFD仿真驱动的序列二次规划(Sequential Quadratic Programming)算法来优化亚音速机翼的结构参数,取得了较高效的翼型。但是由于叶片参数化模型的限制,上述工作没有将翼型参数和结构参数的结合,因此设计自由度不够大。
为了解决上述问题,具有较强翼型描述性能的Class/shape Function Transformation(CST)[4]被应用于描述沿翼展方向的二维翼型变化,并结合结构参数实现对三维无人机旋翼叶片的外形控制。同时,构建基于CFD仿真数据的代理模型作为无人机旋翼的真实物理模型的替代能够大大减少计算量,被广泛应用[5]。文献[6]提出的一种高保真扩展自适应混合代理模型(Extended Adaptive Hybrid Functions,E-AHF),对参数量大的工程黑盒问题具有更高的拟合精度,适用于无人机旋翼的复杂几何外形优化。
综上,建立了如图1的一种新的快速优化框架:首先,建立了基于翼型E387原无人机旋翼的高精度CFD模型,在所有工作转速下误差在4.8%以内;然后,基于CST函数对叶片三维外形进行了参数化,参数共22个,使用拉丁超立方采样[7]进行实验设计并建立了上述[6]中的扩展自适应混合代理模型;最终,在悬停状态下,应用GA遗传算法进行了以旋翼推力为约束,以最小化旋翼扭矩为目标的优化,并对优化结果进行了流固耦合分析,保证了其可行性。

图1 基于E-AHF混和代理模型的叶片优化设计框架Fig.1 E-AHF Model-Based Optimization Framework of Rotor Blades
2 理论基础
2.1 计算流体力学(CFD)
旋翼的空气动力学模型假设为忽略重力三维可压缩粘性流动,其控制方程组(Reynolds Average Navier Stokes Equations)写作:

式中:i,j=1,2,3—x,y,z三个方向;ν—速度;ρf—流体密度;p—流体微元体上的压力;E—流体的能量;τij—因分子粘性作用而产生的作用在微元体表面上的粘性应力的分量;δij—克罗内尔符号(Kronecker delta);qi—流体热通量的分量。
2.2 CST翼型参数化
CST方法[8]是由Kulfan提出的一种描述翼型上下表面坐标点的参数化方法,对翼型的拟合精度较高,且能产生连续光滑的几何外形。该参数化方法分为类函数(Class function)和形状函数(Shape function)两个部分,其拟合公式为:

式中:c—弦长,x、z—翼型沿弦长方向的坐标及其垂向坐标,ψ、ζ—x、z坐标的无因次表达;ζU、ζL—翼型上下表面的无因次坐标;公式最后一项ψ·ΔζU、ψ·ΔζL定义了翼型上下表面的尾缘厚度—描述一行基本轮廓的类函数。
2.3 扩展自适应混和代理模型(E-AHF)
通过对单一代理模型进行误差分析,扩展自适应混和代理模型将不同的代理模型赋予不同的权重进行融合,权重系数和各模型的内置参数由数据集训练得到,最终获得高于任何子代理模型的精度。首先,采用高斯随机过程进行误差估计:

设均值函数为0,协方差由贝叶斯线性回归求得:

其次进行模型评估,引入核函数作为输出响应的函数:
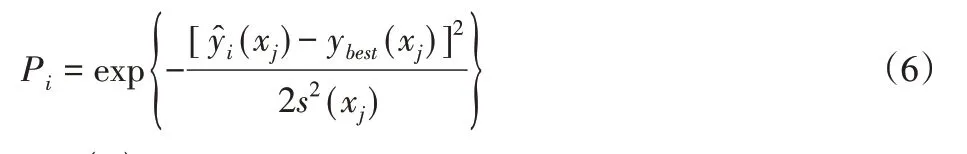
式中:ybest(xj)—组分代理函数在输入变量xj处的最好预测响应,通过基准函数获得。
最终计算局部权重:

模型评估采用决定系数R2以及均方根误差RMSE:

式中:yi—测试点xi处的真值,测试点xi处的代理模型所预测响应为—所有测试点的真值的平均,Ntest—测试点个数。
3 无人机旋翼参数化与仿真
原旋翼采用E387翼型工作参数如表1,实物以及3D模型,如图2所示。

图2 原模型实物(左)及其三维模型示意(右)Fig.2 Baseline Rotor and 3-D Model

表1 无人机旋翼工作参数Tab.1 Parameters of UAV Operating
3.1 旋翼几何参数化
由于旋翼叶片几何外形的复杂性,其参数化过程分为两个部分:首先是对旋翼叶片结构(Platform)参数化,即确定弦长、安装角的分布,前掠或后掠,尖梢比等参数;其次是对二维翼型(Airfoil)的参数化描述,方法诸如B样条插值,PARSEC参数化,Hick-Henne参数化,CST参数化等等。如图3结合旋翼结构参数化,三阶CST翼型参数化方法能够用较少的变量去描述尽可能大的设计空间,实现对旋翼的快速优化设计。

图3 旋翼几何参数化示意Fig.3 Platform Parameters
旋翼半径R=45mm,叶尖、最大弦长处的位置固定,运用6个参数描述旋翼叶片的结构。φtip、ctip为叶尖处的安装角和弦长;φmid、cmid为叶片最大弦长处的安装角和弦长;dmt表征了最大弦长处的位置;ο表示二维翼型几何扭转中心,参数ε描述:当ε=0时,ο位于翼型前缘,前掠为0。原模型结构参数如下表2。
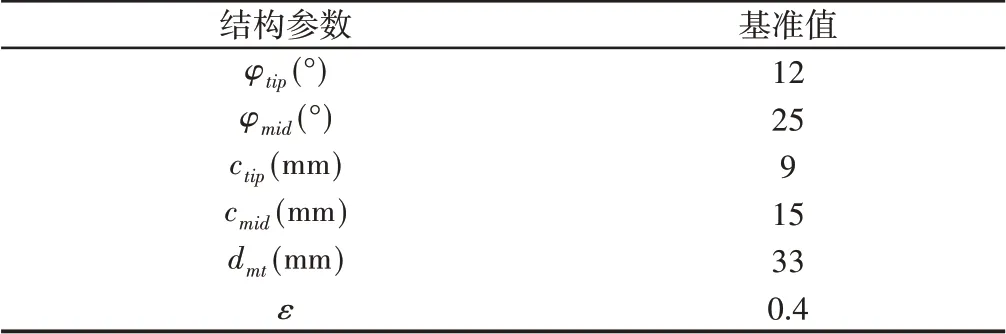
表2 原旋翼结构参数Tab.2 Values of the Baseline Platform Parameters
对原模型二维翼型E387的描述采用三阶CST参数化方法,通过Matlab R2018b优化工具箱中的fmincon函数最小化几何描述误差,确定了上下翼型表面的CST参数。最终,控制悬疑叶片结构的参数6个,叶尖翼型和最大弦长处翼型参数各8个,参数总计22个(详见章节4.1与优化结果一并列出)。
3.2 旋翼流场CFD仿真与实验验证
基于ANSYS ICEM进行网格绘制,应用ANSYS CFX进行CFD仿真计算。流域网格为混合网格,外流域采用结构网格尺寸如图4a所示;内流域采用非结构网格。边界条件设置如图4b,外流域上下表面以及圆柱面为Open;侧面为交界面(Interface),根据转速设置周期旋转边界条件(Rotational Periodicity);桨毂部分、叶片表面设置为Wall。湍流模型采用SST(Shear Stress Transport)模型[9]。

图4 流域网格划分以及边界条件示意Fig.4 CFD Meshing and Boundary Conditions

图6 仿真-实验验证结果Fig.6 Comparison of Thrust between CFD Results and Experimental Data
为了验证CFD仿真结果的准确性,建立旋翼运动的高保真模型,搭建了实验平台,如图5所示,对原旋翼的工作转速范围内的6个转速下的推力进行测量,并与仿真结果进行对比如图4b,其最大误差不超过5%。

图5 实验台展示Fig.5 Experimental Device
4 基于代理模型的优化设计
依照2.1章节中的参数化可以得到有关旋翼三维几何形状的22个设计参数,包括:6个结构参数(记为Pairfoil)和16个叶尖和最大弦长处翼型的CST翼型控制参数(记为Pplatform)。随后进行拉丁超立方实验设计,并进行章节2.2中的叙述的CFD仿真得到训练集和测试集数据建立悬疑扭矩TQ和推力TH的扩展自适应混合代理模型,得到精度如表3。并根据所建立的代理模型进行如方程组(10)下定义的单目标优化以提升旋翼的悬停效率。

表3 E-AHF代理模型精度Tab.3 R2 and RMSE of E-AHF Model
除了旋翼推力TH的约束之外,还将旋翼叶片安装角的负扭作为优化问题的约束之一,这样做有利于提高悬停效率,节省优化算法的搜索时间;另外,还考虑了CST二维翼型参数化以及翼型最小厚度tmax的约束,以保证能够产生真实有效的旋翼外形。

优化算法采用Matlab R2018b内置GA遗传算法[10]。
5 优化结果讨论与流固耦合验证
5.1 优化结果与讨论
优化前后参数对比,如表4所示。

表4 优化前后的参数比较Tab.4 Parameter Values of Optimized Model and Baseline Model
经优化后的叶片正投影形状以及压力分布如图7所示,其中CT、CQ和FM分别为旋翼的推力系数、功率(扭矩)系数和悬停效率。如图8a对比了Y=0.3R、0.7R、0.9R处的截面翼型轮廓并展示了元模型和优化后模型的3D效果图,图8b则比较了二者沿翼展方向的弦长和安装角的分布。

图7 旋翼叶片压力云图Fig.7 Pressure Contour of Baseline Blade and Optimization Blade

图8 原模型与优化模型的对比Fig.8 Comparison between the Optimized and Baseline Model
可见,优化后的旋翼叶片低压面压力分布更加均匀且低压分布面积较广,叶片的有效面积更小,由叶根到叶尖的安装角负扭更大;且相对于原旋翼翼型E387,优化后的旋翼翼型具有较大的弯度。优化后的旋翼叶片的扭矩减少12.5%,悬停效率提高了8.32%,总重相对减少24.23%。
为了检测优化结果是否在不同的飞行状态也表现出良好性能,对优化后旋翼进行了不同转速下的CFD仿真,得到了不同状态下的优化旋翼的工作性能参数,并与原模型比较结果,如图8所示。
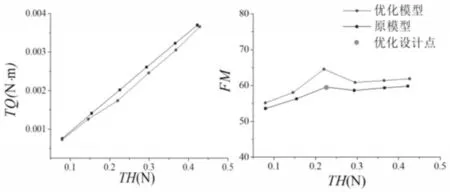
图9 非优化转速下原模型与优化模型性能对比Fig.9 Performance of Optimized Rotor in Off-design Conditions
显然,优化后的旋翼不仅在悬停状态下表现出良好性能,在其他非优化设计点也能减小无人机旋翼扭矩从而提高效率。
5.2 流固耦合验证
为了确保优化旋翼在极限工作状态(17000RPM)下的结构安全性,基于ANSYS WORKBENCH执行了其单向流固耦合分析,结合高保真CFD分析和FEM(Finite Element Method)有限元静力学分析确定其最大应力以及最大变形,判断其是否失效。旋翼叶片主要受到由于自身质量产生的离心力以及在旋转过程中受到的空气作用力(此处忽略叶片重力),叶片的运动与受力分析图,如图10所示。单向流固耦合的网格信息以及结果如表5,可见,优化后的旋翼仍然能保证极限工作状态下的结构安全性。

图10 旋翼叶片受力分析Fig.10 Loads on UAV Rotor Blade

表5 E-AHF代理模型精度Tab.5 Data for FSI of Baseline Model and Optimized Model
6 结论
针对小型无人机旋翼外形提出了一种基于扩展自适应混合代理模型(E-AHF)的快速高保真优化设计框架,并且验证了其可行性。基于CST方法提出了一种简洁的旋翼参数化方法,设计变量共计22个,进行了经过实验验证的高精度CFD仿真计算,得到其悬停状态下的旋翼拉力和扭矩,分别建立E-AHF代理模型,并执行以旋翼拉力、叶片负扭、翼型厚度等为约束,以旋翼扭矩为目标的GA遗传算法,得到的优化后的旋翼叶片的扭矩减少12.5%,悬停效率提高了8.32%,总重相对减少24.23%。最终,我们验证了在不同转速下优化后旋翼的良好性能,并进行单向流固耦合应力分析,验证了其在极限工作转速下的结构安全性。通过比较原旋翼和优化后旋翼的几何外形可见,在低雷诺数下,适当的增加翼型弯度和叶片安装角的负扭能够提高小型无人机旋翼的效率。

