全矢RNN的轴承故障诊断研究

谢远东，雷文平，韩 捷，陈 磊

（郑州大学振动工程研究所，河南 郑州450001）

1 引言

滚动轴承作为旋转机械以至于机械系统领域中关键性的部位，以支持旋转轴正常稳定的工作状态。任何轴承的意外故障可能导致一些负面影响，例如停机时间增加，生产力降低，甚至造成人员安全等重大问题。随着大数据以及深度学习的发展，依靠算力的智能型诊断方法将会逐渐在智能诊断领域中占主导地位。对于模式识别问题［1］，目前可以分为两种应用场景：（1）用于对轴承剩余寿命进行评估预测；（2）对于轴承的故障类型进行分类。对于RUL（可用剩余寿命）预测，可以分为数据采集、指标系统建立、剩余寿命预测。对于轴承故障分类，即原始信号采集以及数据集预处理、信号特征的提取和选取故障类型。

对于轴承寿命预测来说，近几年，合成的健康指标通常是通过一些数据融合技术构建的，其中多维统计特性均方根（RMS）、方差、峰值被转化成一维特征［2］，取得不错的效果。但是还存在以下缺点：（1）不同的传统的静态特征是从时域和频域中获得，其度量和范围是不一致的；（2）很难确定一个故障阈值（FT）不同机器的故障时间（HI）值有一个很大的变化范围。

对于轴承故障分类来说，传统的方法如文献［3］中对信号降噪，使用EMD和LSTA以及SVM进行分类；文献［4］使用小波进行特征的提取进行了对比以验证传统特征提取方法只适用于一些特定的信号，故方法的通用性不强。设计专用网络［5］成为了传统手工提取故障特征不可忽视的缺点，从而影响进一步发展。

深度学习由科研人员提出，通过大量的数据进行非线性拟合的方式，得到数据不同维度的特征。科研人员使用卷积神经网络针对旋转机械中的轴承故障特征进行提取［6］；科研人员利用相空间重构与SVD结合深度置信网络对滚动轴承的故障诊断［7］；科研人员使用深度神经网络结合全矢谱理论对轴承故障中的特征进行提取［8］。

以上均采集的是单通道信号，故提取的故障特征是不完善的，无法准确的表征信号的原始信息，而全矢谱［9］技术结合双通道信息，使数据更加的完备。本文将全矢谱与循环神经网络算法结合并提出基于全矢RNN模型，通过试验对比CEEMD算法以及单通道LSTM算法从而验证了该方法的有效性和优越性。

2 循环神经网络算法

2.1 RNN原理

RNN结构类似于链条，这样的链条结构对于处理序列和列表数据十分有效。例如对于语句进行识别，Xi就是相对应的词语的one-hot向量，A为网络记忆单元，一般有非线性激活函数如tanh或Relu，同时将处理结果作为输入到下一个记忆单元，ℎi为相对应的输出，一般有激活函数softmax处理。

2.2 LSTM向前传播

LSTM（长短时记忆）是相对于循环神经网络的改良版本，由Hochreiter和Schmidhuber（1997）提出以克服RNN难以训练和梯度消失问题［10］，能够学习长期依赖关系。对于每一个单元结点相对于简单RNN，添加了遗忘门、更新门和输出门对于元数据的连接进行更多的非线性的控制。LSTM网络的基础向前传递结构，如图1所示。

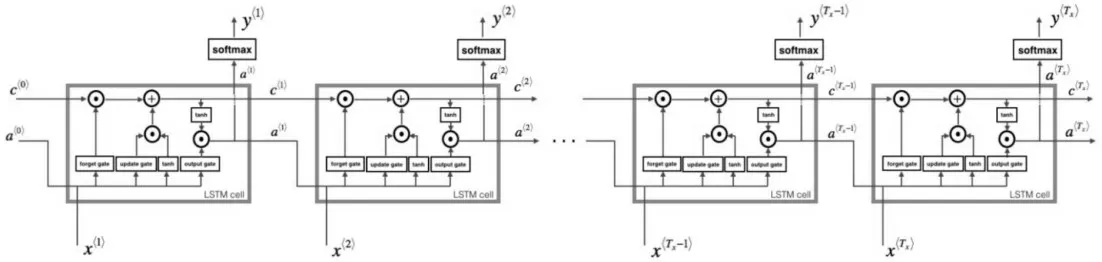
图1 LSTM（长短时记忆）网络向前传播结构图Fig.1 Structure of Long and Short Time Memory Forward

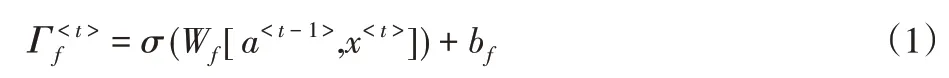
一旦我们遗忘了了所讨论的主题是单一的，我们需要找到一种方法来更新它以反映新主题是复数。以下是更新门的公式：

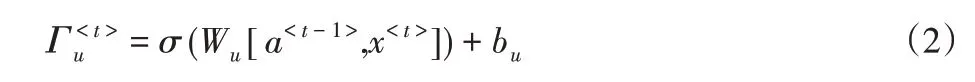
要确定我们将使用哪些输出，我们需要输出门：

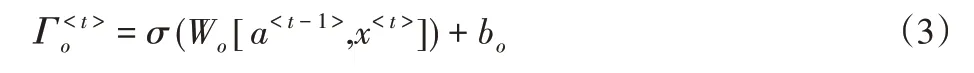
式中：Wf、Wu、Wo和bf、bu、bo—控制遗忘门、更新门、输出门输出的参数矩阵和偏置向量，σ—激活函数，这里通过Logistic Sigmoid激活函数来控制门的开关程度以控制信息的流动，a＜t-1＞—上一个节点的输出。这里的[a＜t-1＞,x＜t＞]是将上一节点的输出和该节点的输入进行合并矩阵操作，式中a＜t-1＞和x＜t＞做如下操作：

要更新新状态，我们需要创建一个新的数字向量，我们可以将其添加到之前的单元格状态。我们使用的等式是：

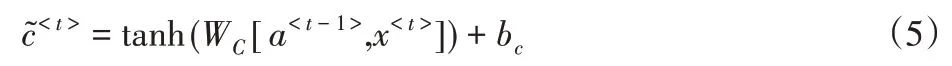
最终新节点状态为：

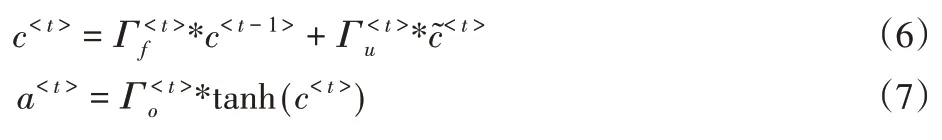
2.3 LSTM向后传递

节点进行向前传递后，需要向后传递获取梯度从而进行优化，基础RNN网络的基础向后传递结构，如图2所示。

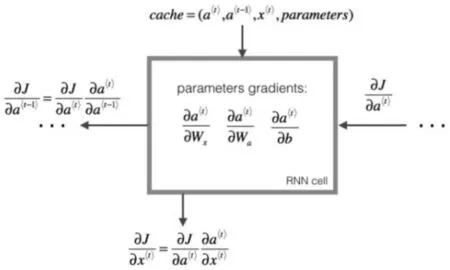
图2 基础RNN网络向后内传播结构图Fig.2 Structure of Base RNN Backpropagation

我们对于基础RNNa＜t＞进行求导，如下：

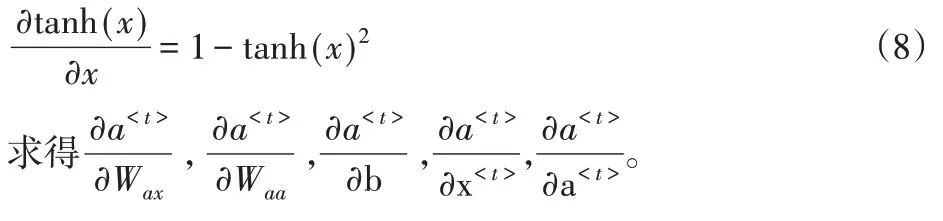
在Base RNN的基础上，使用通过时间的反向传播（Back Propagation Through Time，BPTT）算 法［11］，求 得

最后将计算相对于之前隐藏状态，之前的记忆状态以及输入：

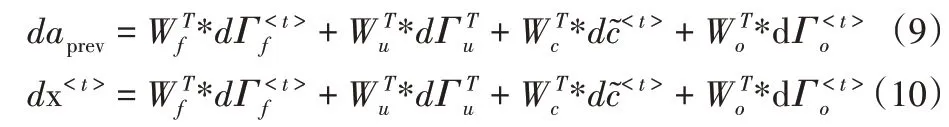
2.4 Adam优化器

这里使用Adam［12］作为优化算法进行参数优化，它计算过去梯度的指数加权平均值v以及指数加权平方值s，并将其存储在变量（偏差校正前）和（偏差校正）中。t代表adam的步数，L是层数，β1和β2是控制指数加权平均值的超参数，α是学习率，是一个很小的数保证分母不为0。

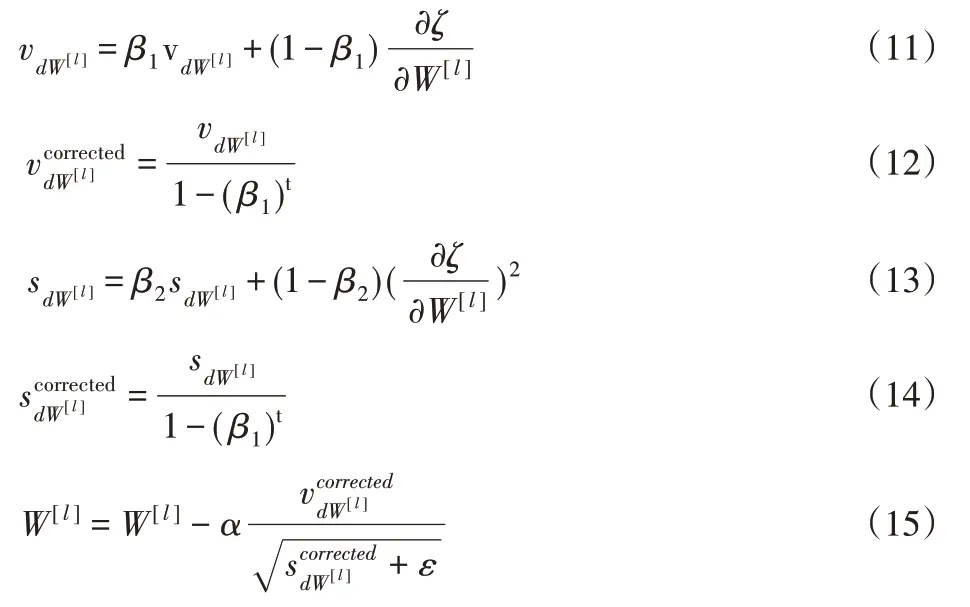
3 全矢谱理论

全矢谱简单理解就是转子的涡流现象是谐波频率的组合，其涡旋轨迹是一系列椭圆。定义椭圆的长半轴是振动强度评估的主要振动矢量，短半轴是振动强度的子振动矢量。而转子在不同谐波频率下的强度是对故障判别的基本依据［13］。

双通道数据{xn}和{yn}（n=0,1,2,…,N-1），傅里叶变换{Xk}和{Yk}（k=0,1,2,…,N-1），令复序列{zk}={xk}+i{yk}，式中i=，通过傅里叶变换得到{Zk}，并结合正反进动得到以下公式：

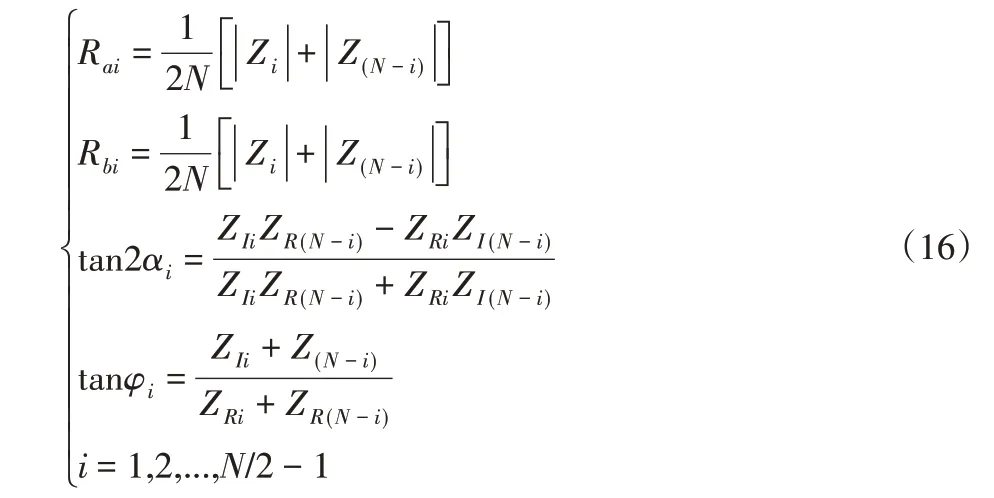
式中：Rai主振矢，Rbi—副振矢，αi—主振矢和x轴的夹角，φi—初相位角。

4 全矢循环神经网络方法

使用全矢谱对同源信号进行融合得到主振矢，使用得到主振矢训练集对LSTM模型进行训练，经过验证集验证并进行参数微调，通过Layer Normalization在通道方向做CHW归一化避免数据分布不一致带来长尾特征提取不到问题，使用Adam作为优化器进行优化，最后在测试集上验证LSTM模型的有效性。如图3所示。

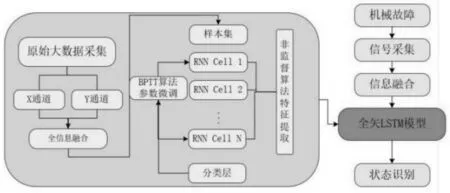
图3 全矢LSTM方法故障诊断流程图Fig.3 Flow Chart of Full-vector LSTM Fault Diagnosis

具体步骤如下：

（1）确定LSTM模型结构，我们选择双向LSTM，相对于LSTM更关注上下文信息的传递性；对样本采样信息中的双通道数据进行全矢融合并得到主振矢谱，作为训练的训练集；

（2）确定训练的超参数训练学习率、确定目标函数θ，确定epoch、batch-size、学习率、节点数、输出节点数、激活函数类型等；

（3）计算全矢LSTM模型每一层的节点状态a＜t＞，通过增加BatchNormalization在通道方向上做归一化，解决输入分布不一致问题，解决梯度消失问题，提高收敛速度即训练时间。

（4）使用Adam算法计算输出结果与标签的损失函数φFV-LSTM，根据BPTT算法fine-tune模型，更新W和b。

（5）将全矢LSTM输出层与使用测试集标签数据做对比，统计正确率，召回率等评价指标。

5 实验研究

使用Center for Intelligent Maintenance at Sinatra University的滚动轴承全生命周期故障数据［14］进行实验。四个Rexnord ZA-2115滚动轴承在的位置，如图4所示。每列包含16个滚动体，节圆直径为71.5mm，滚子直径为8.4mm，接触角为15.17°。通过摩擦带将转速连接到轴上的转速保持恒定在约2000r/min。通过弹簧机构，轴和轴承承受6000磅的径向载荷。所有轴承都是强制润滑的。对于数据集每个轴承上安装了两个PCB 353B33高灵敏度石英ICP加速度传感器（分别装在X轴和与之垂直的Y轴）。所有故障均发生在轴承超过设计寿命1亿转以上的情况下。ICP传感器的采样频率为20 kHz，每次采集了20480个点。信号样本采集间隔为10 min，于2003年10月22号至2003年12月25号持续采集信号保存在2156个文件中，其中前43个文件中的数据的采集间隔是5 min，轴承3、4分别为内圈和滚动体故障。

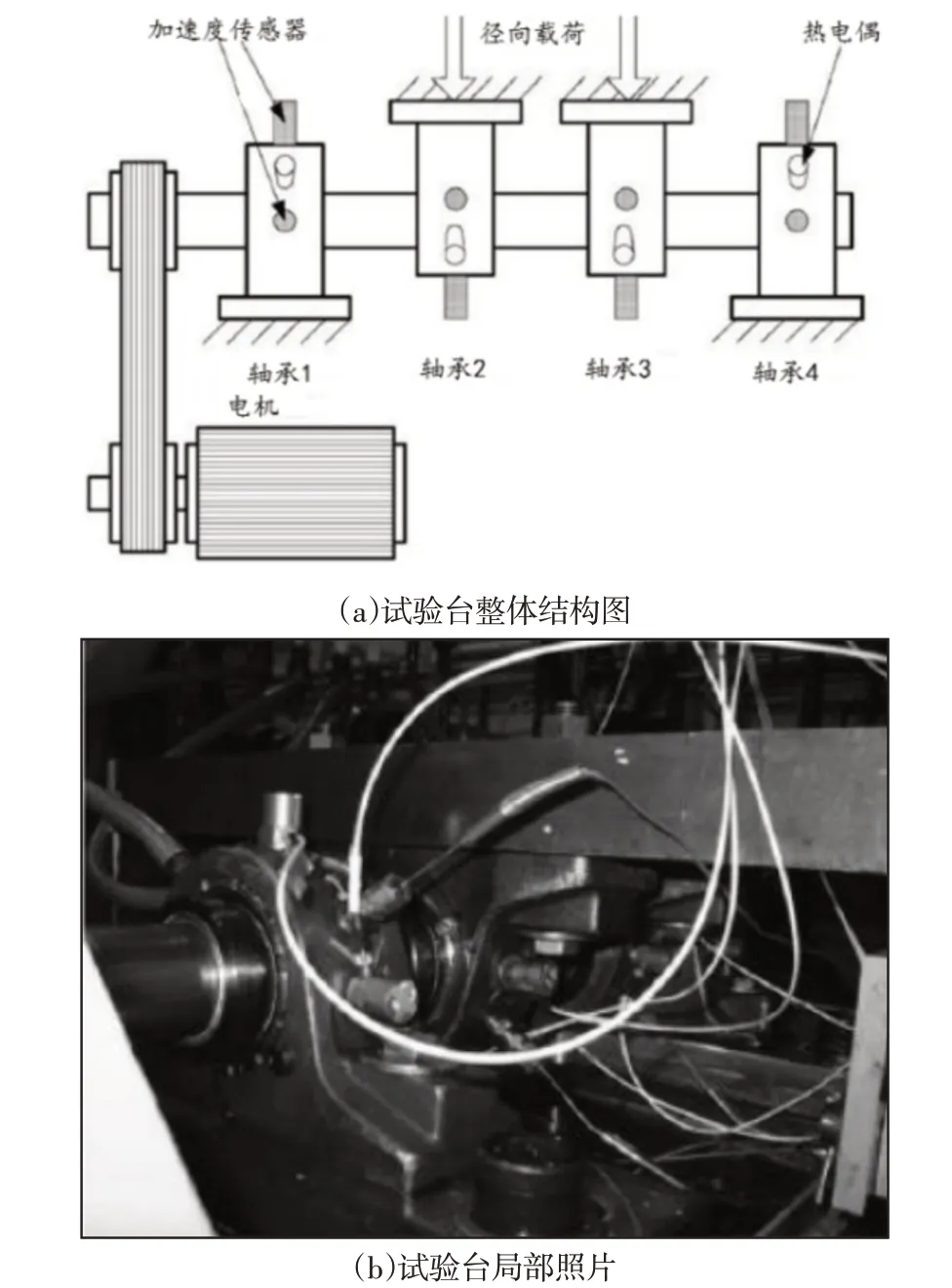
图4 轴承及传感器布置图Fig.4 Bearing and Sensor Placement Illustration

选择test1中的双通道数据进行处理，因为对于三种轴承来说并不是在一开始的情况下就处于故障的阶段，所以在对于三种轴承的数据进行标定标签的时候不能简单的全部标定。我们选择轴承2的全部2156组数据为正常数据。轴承3最终出现了内圈故障，我们对于轴承3的前1800组数据标定为正常数据，在1800到2156组数据标定为内圈故障。轴承4最终出现了滚动体故障，我们对于轴承4的前1600组数据标定为正常的轴承数据，在1600到2156组数据中标定为滚动体故障。由于每一组数据的维度都是20480，在经过全矢谱融合后得到的主振矢的维度为10240，考虑到LSTM节点数太多会导致计算量急剧增加，并且可能会导致梯度在传递过程中出现消失的现象，确定输入节点数为1024，得到试验样本集。最终数据集的长度为64680x1024，虽然其中的每个故障类型的数量不一致，但是是符合现实情况的。训练集和测试集按照8：2的比例分配，试验数据集，如表1所示。

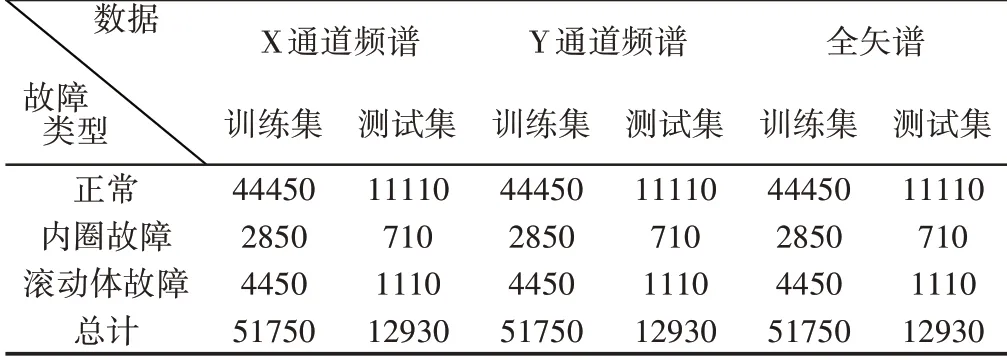
表1 滚动轴承故障类型数据集Tab.1 Rolling Bearing Fault Type Data Sets

由经验［15］设置全矢LSTM网络，设定激活函数为tanh函数，lr为0.05，epoch为400，batchsize为64。考虑到一般的轴承信号中噪声，为了使提取的特征更加的泛化，特征的方差更小，我们采用去噪技术［16］重构输入，其中噪声比率为12%。根据故障结果为正常、内圈故障、滚动体故障确定输出层为3，分别对于全矢LSTM、X通道LSTM、Y通道LSTM的模型的识别效果进行比较。

为了使实验结果更加严谨，我们每次从64680组样本中随机抽取划分训练集和测试集，一共完成了20次重复试验，这里取的是在400epoch中各模型的最高的测试集上的准确率，消除偶然性的影响，全矢LSTM和X通道LSTM测试集以及Y通道LSTM准确率对比，如图5所示。

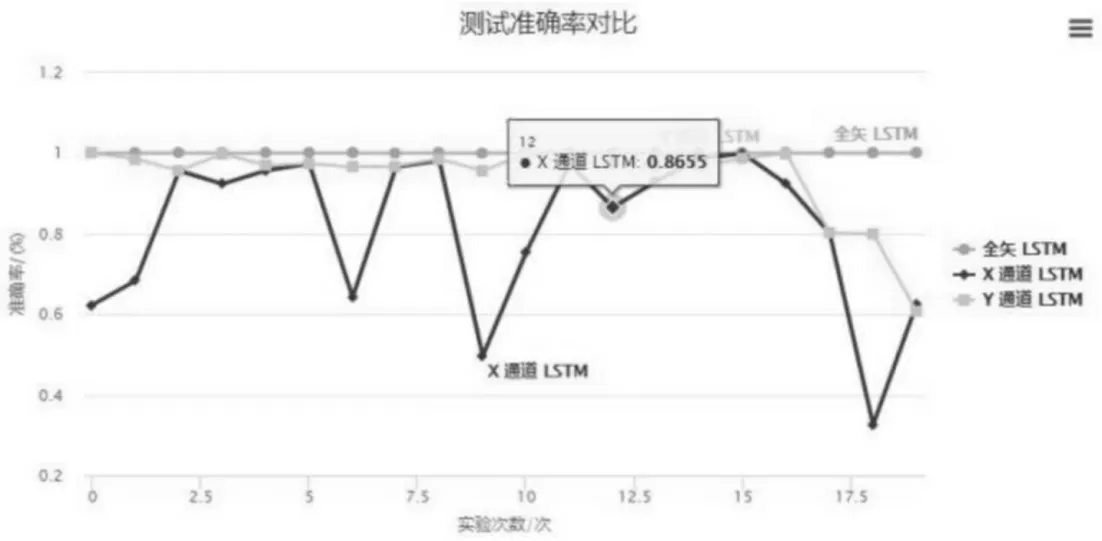
图5 全矢LSTM和单通道LSTM测试集准确率对比Fig.5 Accuracy Comparison between Full-vector LSTM and Single-channel LSTM on Test Set

Epoch=400，验证集上验证的结果，如表2所示。

表2 试验结果比较（平均准确率±标准差）Tab.2 Results Trials（Average Accuracy±Standard Deviation）

从图7和表2可以看出，Y通道LSTM的轴承识别故障准确率要高于X通道LSTM，而全矢LSTM方法在模型的准确率和模型的泛化性上都优于单通道LSTM，证明了全矢LSTM方法是有效的。

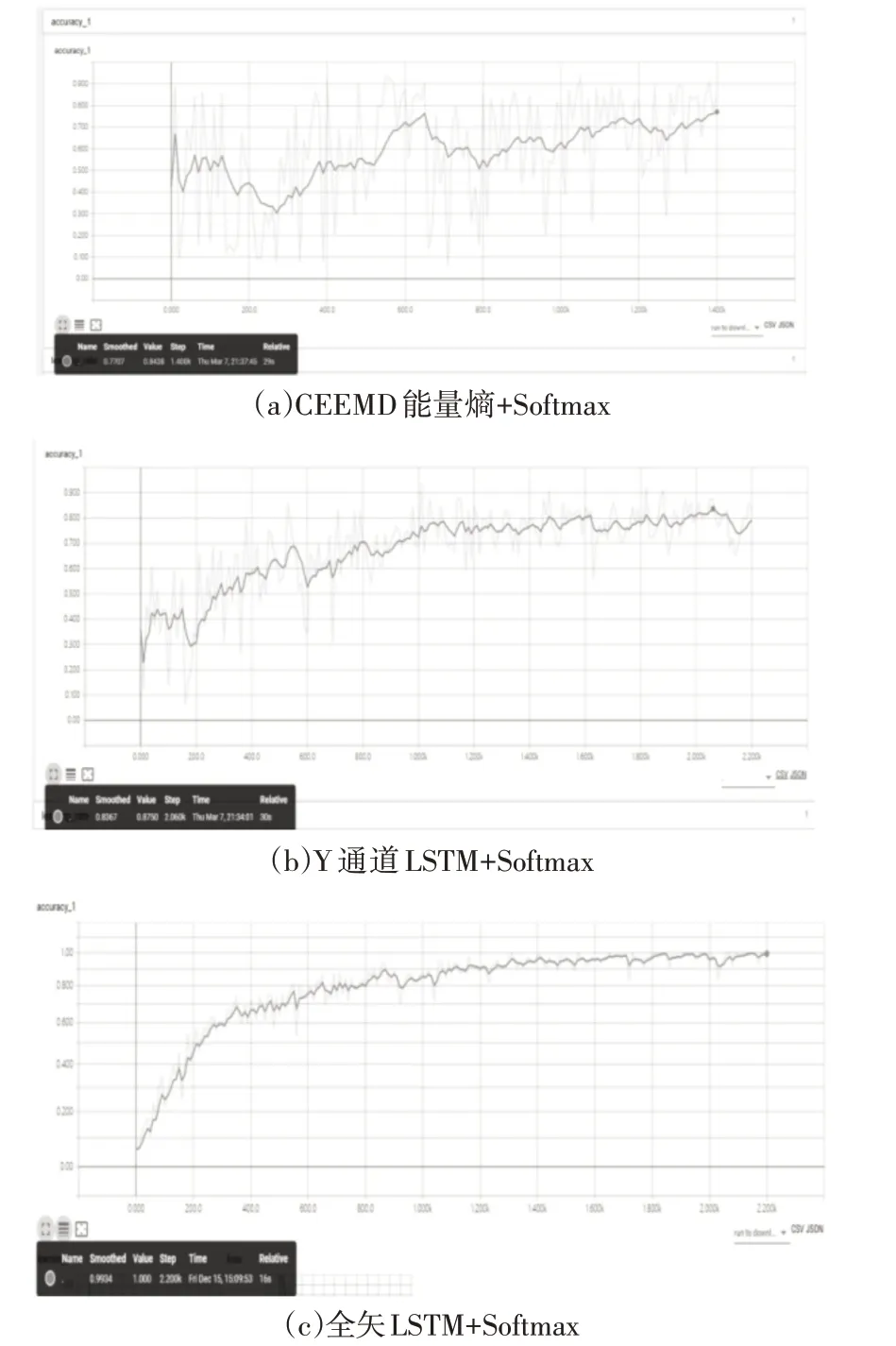
图7 三种方法准确率对比Fig.7 Comparison of Accuracy of the Three Methods

我们分别采集全矢LSTM，X通道LSTM和Y通道LSTM提取的特征向量，用T-SNE非线性降维算法对提取到的特征向量进行降维，得到T-SNE的特征维度图。如图6所示，三种颜色蓝色、绿色、橙黄色分别代表正常状态、内圈故障和滚动体故障的特征分量。从图中可见全矢LSTM方法提取的特征对于故障分类能力特别强，几乎没有误判，而单通道LSTM提取的特征都误判现象，并且对于特征的拟合并不完善，故全信息融合技术是有效以及必要的。

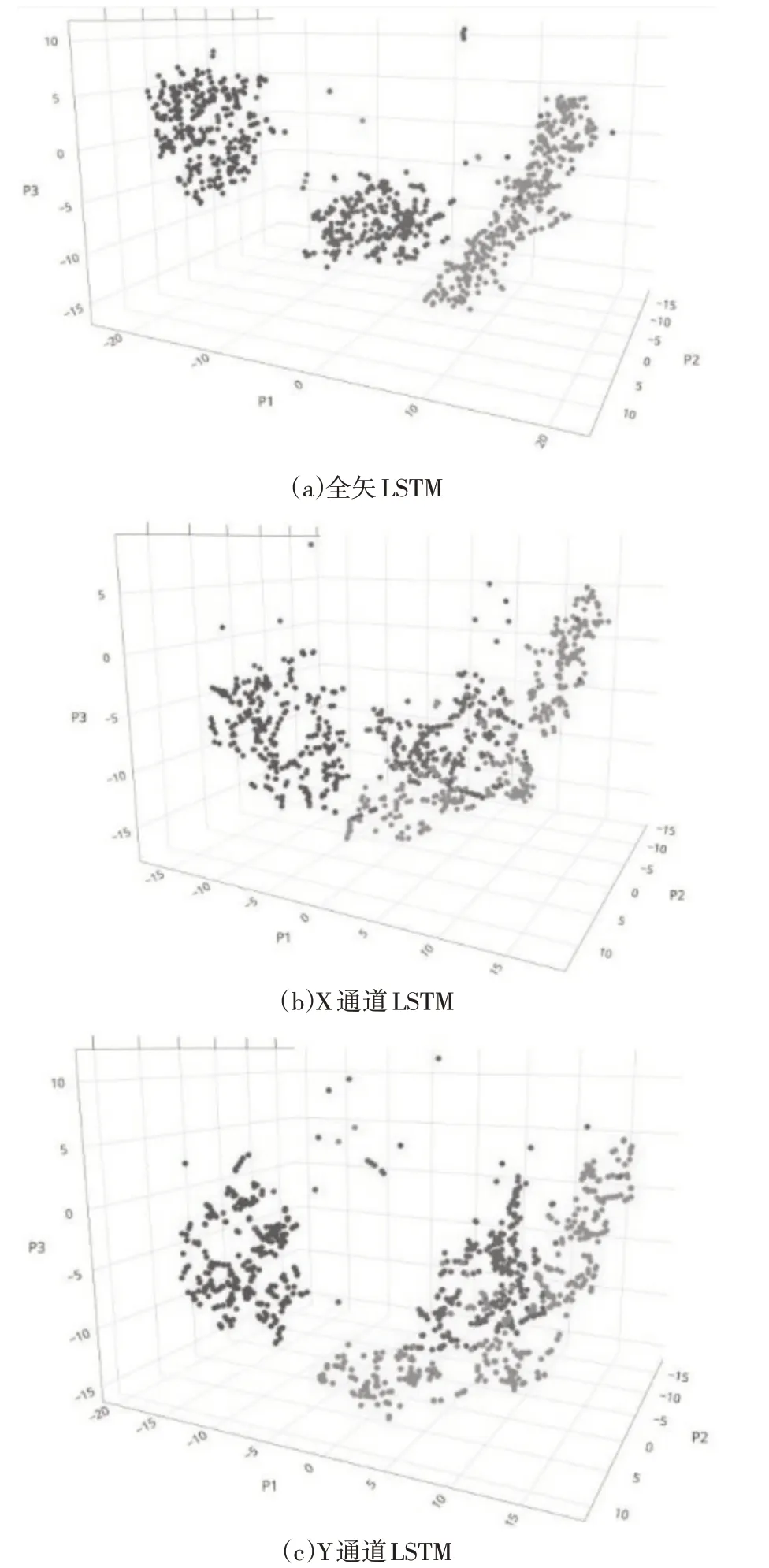
图6 测试集分类结果PCA特征对比Fig.6 Test Set Classification Results

为了验证LSTM相对于手工提取有效特征的优越性，我们选择CEEMD能量熵作为手工特征提取方法的典型代表与Y通道LSTM以及全矢LSTM的特征向量作比较，最后都使用softmax多分类器中，结果，如表3所示。

表3 特征提取方法与softmax结合测试集诊断准确率对比Tab.3 Comparison of Diagnostic Accuracy Between Different FeatureExtraction Methods Combined with Softmax in Test Dataset

由于softmax对于多分类的优化，Y通道DNN和Y通道LSTM都取得比较好的分类效果。由表3和图7所示，CEEMD作为手工特征提取准确率较低，并且出现的波动比较大；而单通道LSTM的准确率有所提升达到83.67%，并且波动变小，表示其泛化性较强；而全矢LSTM的准确率达到99.34%，并且在准确率提升的同时不存在波动，可以进一步验证了全矢LSTM相对于手工提取轴承故障特征，判断轴承故障类型具有很大的优势。

6 结论

经过IMS数据集的验证，全矢谱融合双通道信息，对于数据增强以及模型对于数据的拟合都有明显的作用。通过全矢谱和循环神经网络中的LSTM模型结合得到全矢LSTM模型提高了对于轴承故障诊断分类的准确率以及模型泛化性的全面提升。