加工时间不确定的作业车间滚动窗口动态调度

杨培培，李 明，袁逸萍，李晓娟

（新疆大学机械工程学院，新疆 乌鲁木齐830047）

1 引言

在确定性环境中建立的模型用于实际作业车间生产中时，由于不确定因素存在会直接或间接受到影响，这种影响最终体现在加工时间波动上［1］。动态调度对于加工时间波动多是采用概率论、模糊方法等，处理结果得到的是经验预估值，与实时数值有着较大差距，由此制定的重调度策略便不具备其应有之义［5］［9］。鉴于此，选择将不确定的加工时间作为车间动态调度问题的切入点，具有重要的理论价值和现实意义。

文献［2］将加工时间用区间数表示，对作业车间进行单目标建模并改进交叉策略求解，结果证明此方法可获得较优全局解。文献［3］紧扣关键工序集，设计相应遗传算法，结合滚动时域对相应部分重调度。杨宏安［4］创新采用区间数对提前和拖期区间加以预测，确定待加工工序的开始加工时间。文献［6］选取三种扰动事件，采用事件驱动，实验验证结合滚动窗口建立动态模型的可行性和改进模拟退火遗传算法的有效性。文献［7］混合了滚动策略和布谷鸟算法解决生产车间混流实施的预-反应式调度问题。文献［8］根据划分的扰动类别在混合驱动重调度策略上结合预测控制，采用并行粒子群算法求解验证。文献［10］以柔性作业车间为研究对象，设计相应遗传算法，并予以验证。

本文针对加工时间的不确定，提出加工时间偏差容忍度并设计滚动策略，建立作业车间的调度模型，改进蚁群算法的状态转移规则求解计算。经实验仿真，获得所需的滚动调度策略参数，实验结果显示算法的计算时间较短，计算所得结果质量较优。

2 问题描述与模型建立

首先对作业车间作如下假设：Ⅰ预调度加工时间在排程中受扰动影响而波动；Ⅱ工件按需选取可用资源组合，符合所选资源数量限制；Ⅲ同一资源组合同一时间只能由同一进程使用；Ⅳ工件的加工过程持续不发生中断；Ⅴ紧急工件插入拥有最高的优先级。

符号定义：I为待分配的工件集合；C为单位时间成本；J为工序类别集合，j∈J；R为资源组合的集合，r∈R，rn为资源组合r中的第n类资源集合，n∈N，N为工件所需的资源种类；为工件i在资源组合r的作用下，需要第c类资源的数量，K为资源组合r可以操作的工件数量；为工件i使用资源组合r，倒数第k个位置开始加工的所需时间。

为在s情景下的加工时间，为所有可能的情景；Ω为所有的可行调度集合，X∈Ω。决策变量：工件i属于工序类别j则=1，否则=0；资源组合r可以对工序类别j进行操作则=1，否则=0。对于X∈Ω在情景s∈S下的加工成本：

情景s∈S下的最优调度所对应的加工成本用表示：

定义1调度X的最大遗憾值为：

要使得最坏情景最好，即最大遗憾值最小：

将上述数学模型转换成混合整数线性模型：

由假设Ⅱ可知，需满足：

根据假设Ⅲ，需满足以下关系：

为确保工件和资源组合的匹配性，需遵从以下不等式：

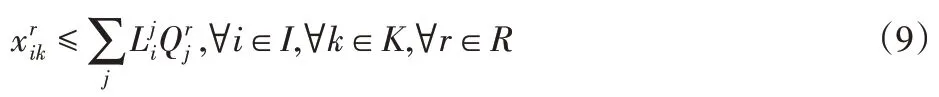
3 滚动调度策略

3.1 加工时间偏差容忍度

不同调度方案总加工时间不相同，不同调度方案对加工时间偏离的稳定能力不同，因此提出加工时间偏差容忍度的概念，对加工时间波动进行定量化控制，表达式为：

式中：max()、max(Ti)—计划完工时间和实际完工时间。根据计算得到δmax，将工件加工时间偏差率与偏差容忍度作比较，大于偏差容忍度时才开启重调度。

3.2 自动触发滚动调度策略

图1 以时间为窗口的滚动过程图Fig.1 Diagram of Rolling Horizon Time-based Windows

当超过加工时间偏差容忍度时需要进行重调度，将已加工完成工件从滚动窗口移除，与此同时，选取数量适宜的待加工工件，进入其中。重调度的启动不影响当前时刻的车间进程。不断进行滚动，直到车间任务全部完工。

其中，ΔT代表时间窗口长度，ΔTp代表预测窗口长度，w(l)表示预测窗口，Ps(l)表示完工窗口，Fs(l)表示等待窗口。

4 改进蚁群算法的状态转移规则

编号为k的蚂蚁，假设它现在处于节点r，下一步将会转移，在众多的节点中，节点s被选中的概率为：

式中：Nu—蚂蚁数量，N—截止目前的迭代次数，经过路径(i,j)的蚂蚁不止一个，其数量用mij表示。信息素在算法局部趋于最优时会不断增加，同时x会随路径上蚂蚁的增多而减少，使得状态转移概率因信息素增长受到的影响得到抑制，进而提高算法全局搜索能力。由mij≤NuN，ηij/max(ηij)≤1得到1≥xij≥xmin=1/( 1+δ)。x强度大小用δ加以控制，xmin随δ减小而增大，蚂蚁爬经路径数在状态转移规则中的权值也随之减小。节点r到节点s的信息素；—节点r到节点s的可见度；选用字母α—信息素，β—可见度偏重系数，分别体现着和在转移概率中的重要程度。由公式（13）计算可见度：

式中：工件进入加工窗口前需要等待，时间用twait表示。在算法实现时取b=2。计算后，重新选择一个节点，使用轮盘赌随机从待加工工件集选取，记录下节点的起始时间，进而计算等待加工时间和加工完成的时间。

5 实验仿真分析

5.1 参数设定

5.2 动态调度参数试验

偏差容忍度值和最佳窗口步长无法依据专家经验等获取，且目前无法根据作业车间生产实际案例采集实时生产数据，故用4阶爱尔朗分布方法予以模拟。对相同规模的同一个算例，分别进行10次实验，{I,J,C,R}分别取值{3 0,350,2,4}，变量设为10个偏差容忍值。记录下最大完工时间，滚动次数，目标函数值以及资源利用率。得到对比结果如表1所示：当大于0.25后，自始至终都没有启动重调度，显然此种情形车间无法应对扰动，当取值降低两个量级，滚动次数急速增大，即局部重调度频繁地进行，不但浪费资源，多数情况下还会扰乱整个生产进程。分析可知，在满足最大完工时间最小前提下，取值为0.1时，滚动次数较少的同时满足调度要求。

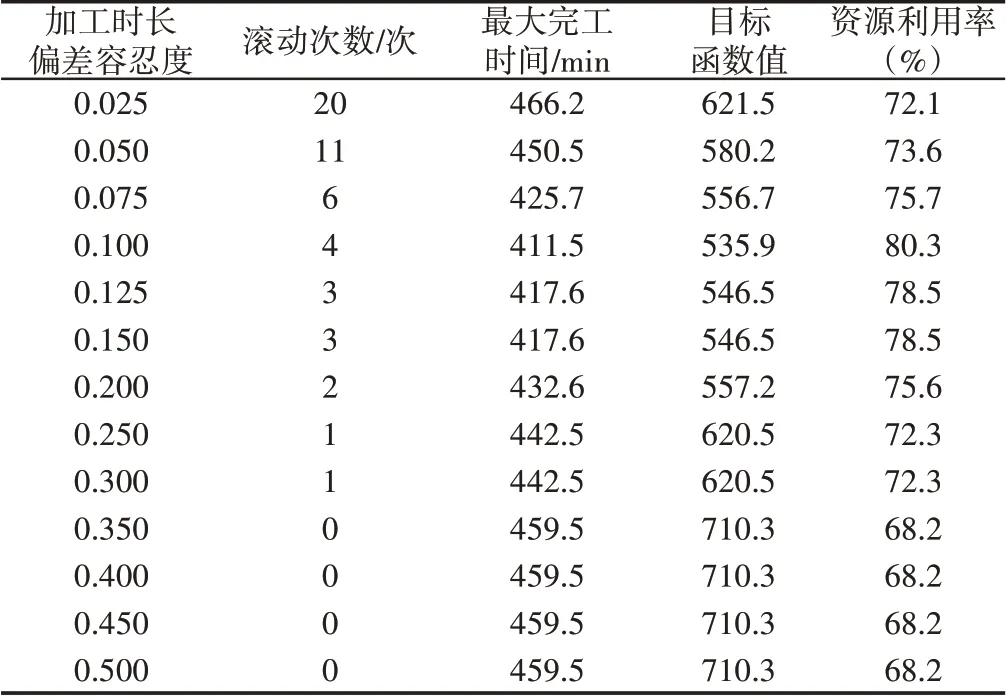
表1 不同加工时长偏差容忍度试验结果Tab.1 Comparison of Different LDT Scheduling Results

将事件驱动应用在紧急工件到达的情况下，其余使用周期驱动。针对同一规模的算例，分别设置不同的步长进行试验，如表2所示：当ΔT=90～100，滚动次数为4～5次时，可取得全局最优得调度方案。

表2 窗口步长不同的重调度结果对比Tab.2 Comparison of Rescheduling Results with Different Size Rolling Windows

5.3 动态调度策略可行性分析

采用回归分析的方法，确定重调度时刻与调度目标最大遗憾值之间的相关关系。拟采用多项式回归模型，假设如下：

式中：xt—重调度的时刻，yt—最大遗憾值，且β1＞0，β2＞0，…，βk＞0。令多元一次线性方程为：

由最小二乘法原理可知，回归曲线就是当残差平方和εt～N(0,σ2)达到最小的曲线，令…-bkxtk)2，要使sse最小，则有：

求解并整理可得：

在进行了50次仿真后得到一些点值，采用散点作图得到回归曲线，如图2所示。根据最小二乘法由式（17）、（18）求得α1=715.3，β1=-1.535，β2=0.003026，回 归 方 程 为yt=715.3-1.535xt+0.003026。

图2 最大遗憾值的回归曲线Fig.2 Maximum Regret Value Regression Curve

分析总结，当加工时间的偏差发生预调度前期，一般不启动重调度，因为在后续生产过程中的时间缓冲可将其吸收；如果发生在后期，也多维持原调度，这时任务大多已经完成加工，预调度鲁棒性能也已发挥，此时调整得不偿失。

5.4 动态调度算法性能试验

将基本蚁群算法（Ant colony optimization，ACO）、标准遗传算法(GA)与设计的改进的蚁群算法（Improved ant colony optimization，IACO）分别进行验证。GA采用实数编码，种群大小为100，个体为a维的向量，其中a为工件数量，每个基因表示工件i，i=1,2,···，I表示被采用的资源组合的编号。为有效评价算法的性能以平均计算时间Tavg、目标函数值Z(X)作为算法评价指标。

如表3所示：分析可知对于不同规模算例，GA计算效率高于ACO，而ACO解的质量高于GA。IACO比ACO求得的解的质量更高，求解速度也更快；当I，J，R相同时，Z()X随C的增大而增大；当I，J，R相同时，Z()X随R的增大而减小，可见解的质量会随着可以利用资源组合数量增加而改善；当I，C，R不变而J增大时，目标函数值变大；当J，R和C相同时，目标函数值随I的增大而增大，而解的质量变差是由于问题规模的增大。

表3 规模不同的算例问题结果对比Tab.3 Comparisons of the Results of Different Scales Examples

6 结论

针对加工时间不确定的作业车间动态调度问题，提出一种基于滚动技术的混合驱动重调度策略。只有紧急工件到达时，采用事件驱动机制。提出加工时间偏差容忍度来过滤掉不必要的重调度。改进状态转移规则，提高蚂蚁算法全局收敛性能。通过实验仿真，对滚动调度策略参数进行分析并对动态调度算法性能进行比较验证，得出较优参数并验证了算法在计算时间和计算结果上均较优。