广义二项指数和的四次幂均值

王婷婷

(西北农林科技大学 理学院， 陕西 杨凌 712100)

设整数k>h≥1及整数m,n,如果q≥3是一个整数,则二项指数和G(m,n,k,h,χ;q)定义为

其中:e(y)=e2πiy;χ表示模q的一个狄利克雷特征。

这些二项指数和在解析数论研究中占有非常重要的位置，特别当q=p为奇素数时, 它们与有限域上的傅里叶分析密切相关。正因为如此，许多学者研究了G(m,n,k,h,χ;q)的各种性质, 并得到了一系列重要的结果[1-10]。例如,文献[9]证明了恒等式

其中p表示满足(n,p)=1的奇素数。

最近,文献[11]研究了一般化的二项指数和的四次均值，并证明了以下结论:

如果p是满足(3,p-1)=1的奇素数,n为满足(n,p)=1的任意整数,则对任意狄利克雷特征λmodp,有恒等式

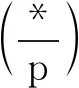
由文献[11]可知，此问题的难度较大,研究进展非常缓慢。

显然，文献[11]只考虑了特殊情况(p-1,3)=1，对于p≡1 mod 3，目前未见相关研究。但是这种情况(p≡1 mod 3)非常重要, 因为它与广义Kloosterman和密切相关。事实上文献[7]证明了对于任意整数m满足(m,p)=1,有恒等式

此外，还有一些相关的研究工作可参考文献[12-14],这里不再一一列举。

本文受到文献[11]研究的启发, 同时也想弥补其中的不足，于是提出：对于p≡1 mod 3,是否存在广义二项指数和四次均值

(1)

的一个确切的计算公式？

本文利用初等和解析方法研究了(1)式的计算,并得到了一些确切的计算公式,即证明了如下结论。

定理1设p为奇素数且满足p≡1 mod 3,n为任意整数且满足(n,p)=1，则对任意狄利克雷特征λmodp,有恒等式

其中：d由d≡1 mod 3和4p=d2+27b2唯一确定；χ表示模p的任意非实特征；ψ为模p的三阶特征；M(χ,ψ)定义为

定理2设p为满足p≡1 mod 3的素数。若特征χmodp满足χ3≠χ0，则有恒等式

推论1设p为满足p≡1 mod 3的素数，χ为模p的任意非实特征，则有渐近公式

其中E(p)满足估计式|E(p)|≤29p2。

1 几个简单引理

本节给出几个定理证明中必要的引理。下文将用到经典高斯和的一些性质和基本理论,这些内容可参考文献[15-16]。经典高斯和τ(χ)表示为

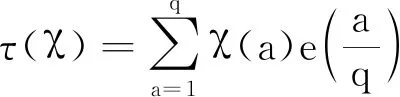
引理1设p为奇素数且满足p≡1 mod 3。对任意整数n满足(n,p)=1,若λ为模p的任意狄利克雷特征,则有

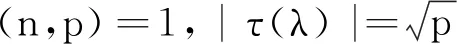
(2)

可得

(3)

因为p≡1 mod 3,则同余方程x3≡1 modp有3个解,即x≡1、α、α2modp。若存在特征χmodp满足λ=χ3，则有λ(1)=1,λ(α)=1和λ(α2)=1，由(2)式和(3)式可得

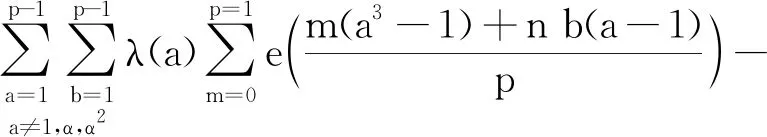
p(p-1)-pλ(α)-pλ(α2)-p=

p(p-1)-2p-p=p(p-4)。

(4)

若λ=χ0为模p的主特征，由(2)式可得

利用(4)式的证明方法可得

p(p-1)-2p-1=p2-3p-1。

(5)

若λ≠χ0、χ3,则1+λ(α)+λ(α2)=0，由(2)式和(3)式可得

λ(α)p-λ(α2)p-p=p(p-1)。

(6)

结合(4)—(6)式可得引理1。

引理2设p为奇素数且满足p≡1 mod 3。若λ表示模p的任意给定的特征, 则对任意非主特征χmodp和任意整数n满足(n,p)=1,有

证明由经典高斯和及模p简化剩余系的性质,可得

(7)

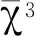
引理3设p为奇素数且满足p≡1 mod 3,ψ表示模p的任意三阶特征,则对任意特征χmodp且χ3≠χ0，有恒等式

证明注意到ψ(-1)=1,由高斯和及模p三阶特征的性质,可得

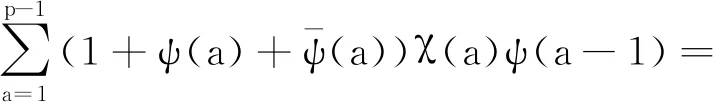
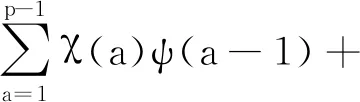
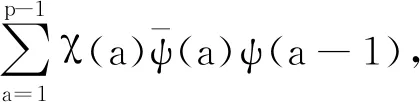
(8)

(9)

同理可得

(10)

(11)

结合(8)—(11)式可得

(12)

对任意特征χmodp，高斯和的三项乘积公式表明

(13)

由(12)式和(13)式可得

(14)

即证引理3。

引理4设p为奇素数且满足p≡1 mod 3,则对任意三阶特征ψmodp,有恒等式

其中d是由d≡1 mod 3和4p=d2+27b2唯一确定的整数。

证明由模p的三阶特征ψ的性质可得

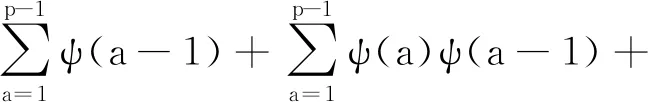
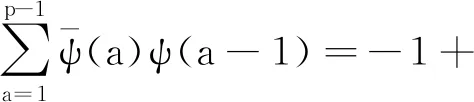
(15)

由文献[10]和[12]可知

(16)

结合(15)式和(16)式可得

p+4-2d。

即证引理4。

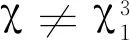
证明因为p≡1 mod 3，令θ≠1为同余方程x3≡1 modp的一个解,即θ3≡1 modp且(p,θ-1)=1。由模p简化剩余系的性质可得

(17)

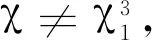
即证引理 5。

2 定理的证明

对任意奇素数p满足p≡1 mod 3及任意整数n满足(n,p)=1,由特征χmodp的正交性可得

(18)

对于η≠χ0modp，若λ=η3，则由引理1、引理2及引理3可得

p2(p-4)2+

p2(p-4)2-9p2-

p2(p2-8p+7)-

p2(p-1)(p-2)+

p2(p2-8p+7)-

(19)

其中用到了恒等式

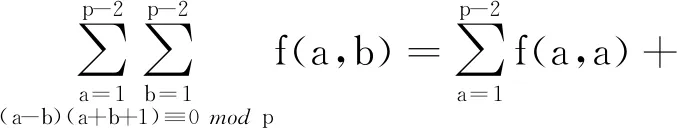
再利用模p简化剩余系的性质可得

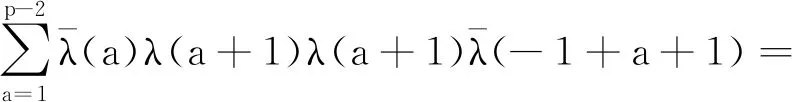
(20)

(21)

结合(19)—(21)式可得

(22)

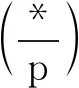
若λ=χ0，由模p特征的正交性，结合引理1、引理2、引理4以及(22)式的证明方法可得

(p2-3p-1)2-p2(p-4)2-

2p2(p-1)(p-2)-p2(p-1)+

(p2-3p-1)2-p2(p-4)2-

2p(p-1)(p+4-2d)=

(p-1)(2p3-5p2-15p+4dp-1)。

(23)

对于其他的λ，由引理1、引理2和引理5可得

(p2-p)2=

(p2-p)2=

p2(p-1)(p-2)-2p2(p-1)+(p2-p)2=

p2(p-1)(2p-5)。

(24)

结合(18)、(22)、(23)和(12)式可得

其中：d是由4p=d2+27b2和d≡1 mod 3唯一确定的常数；ψ为模p的三阶特征；M(χ,ψ)定义为

即定理1得证。

定理2的证明由引理3可直接推出。

3 总结

本文证明了两个主要定理，针对奇素数p≡1 mod 3，分别获得了两个恒等式，得到的结果与广义Kloosterman和的混合幂均值密切相关，为进一步研究此类问题提供了一些新的思路和方法。