一般化的D.H.Lehmer问题及其证明
王婧哲
(内蒙古财经大学 统计与数学学院, 内蒙古 呼和浩特 010070)

文献[2]对这一问题进行了首次研究,并证明了渐近公式:
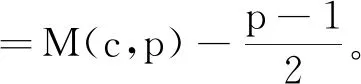
其中exp(y)=ey。
本文的主要目的是将D.H.Lehmer问题进行一般化,即研究N(h,k;q)的渐近性质。我们将利用初等方法以及三角和的估计给出N(h,k;q)的一个较强的渐近公式,即证明以下定理。
定理设q>2为整数,1 其中:φ(q)表示Euler函数;d(q)表示Dirichlet除数函数。 特别当q=p,k=2且h=1时,有以下推论。 推论对任意奇素数p,有渐近公式 注本文使用的初等证明方法虽然非常简洁,但是也有其缺陷, 即不能建立其误差项与DirichletL-函数加权均值间的密切联系,因而利用这种方法很难给出类似文献[5]中误差项均值的一个渐近公式。如何建立这种一般化渐近公式中的误差项与DitichletL-函数加权均值间的密切联系也是一个很有趣的数论问题。 本节利用初等方法以及三角和的估计给出定理的直接证明。文中需要初等数论以及三角和估计的有关内容,这些均可以参阅文献[9-10], 此处不再重复。 对任意正整数q>1以及整数n,有三角恒等式 (1) 其中e(y)=e2πiy。 应用(1)式,有恒等式 N(h,k;q)= W1+W2+W3+W4。 (2) 现在分别估计(2)式中的Wi(i=1,2,3,4)。首先,估计主项W4。注意到 以及 h+1+k-1-(h+1)+1=k, 并考虑到k为给定的正整数,所以有渐近式 (3) 为估计(2)式中的其他和式,需要用到解析数论中关于Kloosterman和的上界估计,有关内容可参阅文献[11-13],相关工作也可以参考文献[14-15],此处不再重复。 (4) 其中:d(q)表示Dirichlet除数函数;(m,n,q)表示m、n及q的最大公约数。 对任意正整数1 可得估计式 (5) 当(k,q)=1时,结合(4)、(5)式及W1的定义可得 (6) (7) 同理,可得估计式 (8) 及 (9) 现在结合公式(2)以及估计式(3)—(9),即可推出渐近公式 于是完成了定理的证明。 本文的主要结果是将D.H.Lehmer提出的一个问题进行了进一步的推广, 并利用初等方法以及三角和估计对其计数函数给出了一个较强的渐近公式。这一工作是对已有工作的进一步丰富和完善,其中的研究方法对相关问题的研究有借鉴作用。1 定理的直接证明

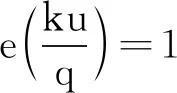
2 结语

