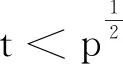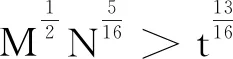一类指数和的加权均值

秦珍珍，张天平

(陕西师范大学 数学与统计学院， 陕西 西安 710119)

近年来, 很多学者研究了指数函数gx在剩余系中的分布问题, 它不仅是数论研究的重要问题,还可以应用在密码学以及伪随机序列生成器中。

给定素数p,设g满足(g,p)=1且模p的乘法阶为t,定义指数和

集合S取连续整数集[1,X)时，Korobov[1]得到了

(1)

其中X≤t。其证明过程需用如下重要结果:

(2)

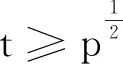
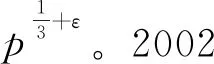
(3)

成立,但对于较小的t没有得到其非平凡的结果。文献[3]进一步得到了当t≥pε时,对于充分大的Q,p∈[Q,2Q]时,至多除了Q5/6+ε个素数p外(3) 式都成立。

此外,对于经典的Kloosterman和

Estermann[4]于1961年给出

目前认为这一估计是最好的。因此,很多学者尝试通过对Kloosterman和加权求均值来进一步研究是否存在相消性。例如,Kuznetsov[5]利用固定m、n,对模q求和的加权均值来研究Linnik猜想。与此相对应,文献[6-11]通过固定模q,对系数m、n分别求和来研究Kloosterman和的加权均值,相关结果都有重要应用[10-14]。

注意到对p不加限制时, 对于较小的t很难得到(2)式的非平凡上界估计。本文借鉴研究Kloosterman和的思路,利用文献[9]的方法来研究(2)式的加权均值,寻求当t取较小值时的非平凡上界估计。

给定集合I={K+1,…,K+M},J={L+1,…,L+N},并且M≤p,N≤t，复数序列A={αm}m∈I，B={βn}n∈J，定义以下两种加权和

(4)

以及

(5)

利用(2)式容易得到其平凡上界

(6)

和

(7)

利用文献[9]中的方法可以得到(4)式的非平凡上界。而(5)式的情形更为一般,其估计较(4)式也更为复杂一些。另外,作为(4)式的应用,可以估计(1)式的如下均值：

本文主要证明(4)、(5)式中两个和式的非平凡上界, 证明过程中需用到以下范数。

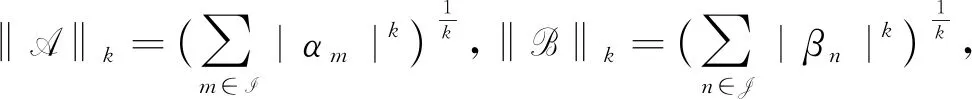
为了方便与所得新结果进行比较,将(6)、(7)式改写为

(8)

(9)

1 预备知识

引理1对于固定的整数m≥1,有

证明见参考文献[15]中定理8.1。

引理2设q为正整数,u、L和N为任意的整数且N≥1,则有

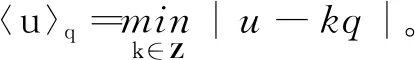
证明见参考文献[16]中的式(8.6)。

为得到加权指数和的上界估计还需引入同余方程

gx1+gx2≡gx3+gx4(modp),

K

其中X≤p。设I是上述同余方程的解数。

证明见参考文献[17]中的定理6。

2 主要结果

定理1设p是素数，t是g模p的乘法阶，且N≤t，则

S(A;I,J)≪(‖A‖1‖A‖2)1/2p1/4t5/8N3/8。

证明交换求和次序并利用引理2,可以得到

其中

(10)

±x>ei-1t/N},i=1,2,…,H。

(11)

由此可得

其中

固定整数r≥2，应用Hölder不等式，则

将内层和展开并交换求和顺序, 可得

其中利用了引理1(三角和的正交性)。

|γx|≪e-iN。

现在应用引理3并且令r=2,则

以及当i>0时有

因此

定理1得证。

注记1若将定理1结果用无穷范数表示为

(12)

注记2当M=p时,由定理1的证明可知并不会改变定理的结果,即

(13)

推论1设p是素数，t是g模p的乘法阶，且X≤t，则

(‖A‖1‖A‖2)1/2p1/4X5/8。

证明由三角和的正交性可得

其中

ej-1t/X},j=1,2,…,T。

由此利用定理1可得

(‖A‖1‖A‖2)1/2p1/4X5/8。

注记3若将推论1的结果用无穷范数表示为

定理2设p是素数,t是g模p的乘法阶, 且N≤t,则

S(A,B;I,J)≪(‖A‖2‖B‖2)p1/2t13/16N3/16。

证明应用Cauchy不等式可得

|S(A,B;I,J)|2≤(‖A‖2‖B‖2)2

mgy)et(nx-ny)=

(mgy+z-mgy)et(nz)。

交换求和顺序并应用引理2得

|S(A,B;I,J)|2≤(‖A‖2‖B‖2)2·

(‖A‖2‖B‖2)2·

其中

对于每一个固定的y,类似定理1的证明可得

由此可得

S(A,B;I,J)≪‖A‖2‖B‖2p1/2t13/16N3/16。

定理2得证。

注记4若将定理2结果用无穷范数表示为

(14)

注记5当βn≡1时，有

S(A,{1}n∈J;I,J)=S(A;I,J)。

可知当βn≡1时定理2的结果比定理1的结果较弱,但定理2的适用范围更为广泛。