旋转析问题本质 相似显以静制动
——以“旋转构造相似三角形”专题复习为例
曹火强 (江苏省南通市通州区二甲中学 226321)
通过旋转变换,求点的运动轨迹或线段的最值问题,一直是全国各地中考的热点和难点,这类问题中常常涉及线段的旋转变换,甚至是动态图形的旋转.仔细分析问题本质,会发现这些题型具有一定的共性:所给图形大多线条简单,在问题的解决上,需理顺点、线、形的“主从”关系,充分挖掘隐藏的条件或图形,进而通过旋转变换构造相应的辅助线来解决.基于此,笔者拟以“旋转构造相似三角形”专题为例,通过对“题源”的拓展与延伸,不断提升中考复习专题的空间与品质.
1 “题源”——旋转全等形
在旋转构造相似的专题复习中,首先从一道经典的题目入手,因其可塑性强,我们将它作为“题源”可以改编出很多题目,其中隐含着一个常见的几何模型——旋转全等形.

图1
例1如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为BC边上一动点(不与点B,C重合),连结AD,将线段AD绕点A逆时针旋转90°,点D的对应点为E,连结CE.则线段BD和线段CE的数量关系为,位置关系为.
简析 易证得△ABD≌△ACE,那么就有BD=CE,∠ACE=∠ABD=45°,所以EC⊥BC.
说明 引导学生理解将线段AD绕定点A旋转,其实就是将线段AD所在的△ABD绕定点A旋转90°至△ACE,并进一步得到结论:点D在边BC上运动时,点D旋转后的对应点E就在过点C且垂直于BC的垂线上运动,由此确定动点E的轨迹为一条定线段,从“动”中发现“定”的本质.
为了让学生灵活运用旋转构造全等三角形,笔者带领学生进行变式训练.
变式1如图2,在Rt△ABC中,∠BAC=90°,AB=AC,D为△ABC形内一点,若∠ADC=135°,BD=3,CD=1,请直接写出线段AD的长.

图2 图3

由条件的等价性,也可如图3,将△ACD绕定点A顺时针旋转90°至△ABE,同样能求得AD的长为2.
若将△ABC形内一点D移到三角形外,还能不能快速求出线段AD的长呢?
变式2如图4,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=3,CD=1,请直接写出线段AD的长.

图4 图5
简析 将△ABD绕定点A逆时针旋转90°至△ACE,可求得AD的长仍为2.或如图5,将△ACD绕定点A顺时针旋转90°至△ABE,同样可得AD的长为2,不过这种方法需先证明点C,D,E在同一直线上.
说明 虽然将点D从形内移至形外,但解题方法仍然与变式1相同,这就是“形”变而“理”不变.通过以上变式的训练,使学生在举一反三中洞查各题的本质,通过绕定点旋转,构造出全等桥梁,在动态过程中找出不变的量,掌握以静制动的解题策略,提升学生的思变能力.
2 拓展至“旋转相似形”
全等与相似是一对“好兄弟”,常常形影不离,那么我们不禁会想,在绕定点旋转时是不是需要拓展至构造“相似”这一桥梁呢?我们还是从特殊直角三角形的旋转入手进行探究.

图6
例2如图6,在△ABC和△ADE中,∠BAC=∠DAE=90°,点D在BC边上(不与点B,C重合),且∠ABC=∠ADE=60°,连结CE.则线段BD和线段CE的数量关系为,位置关系为.


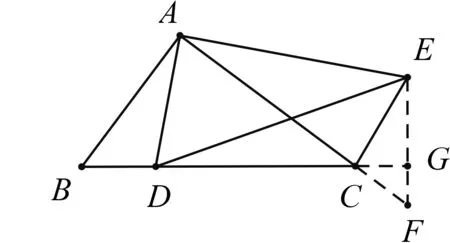
图7
拓展1如图7,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,D为BC边上一动点,连结AD,以点A为直角顶点作Rt△ADE,并且使∠ADE=60°,连结CE.求线段CE长的最小值.



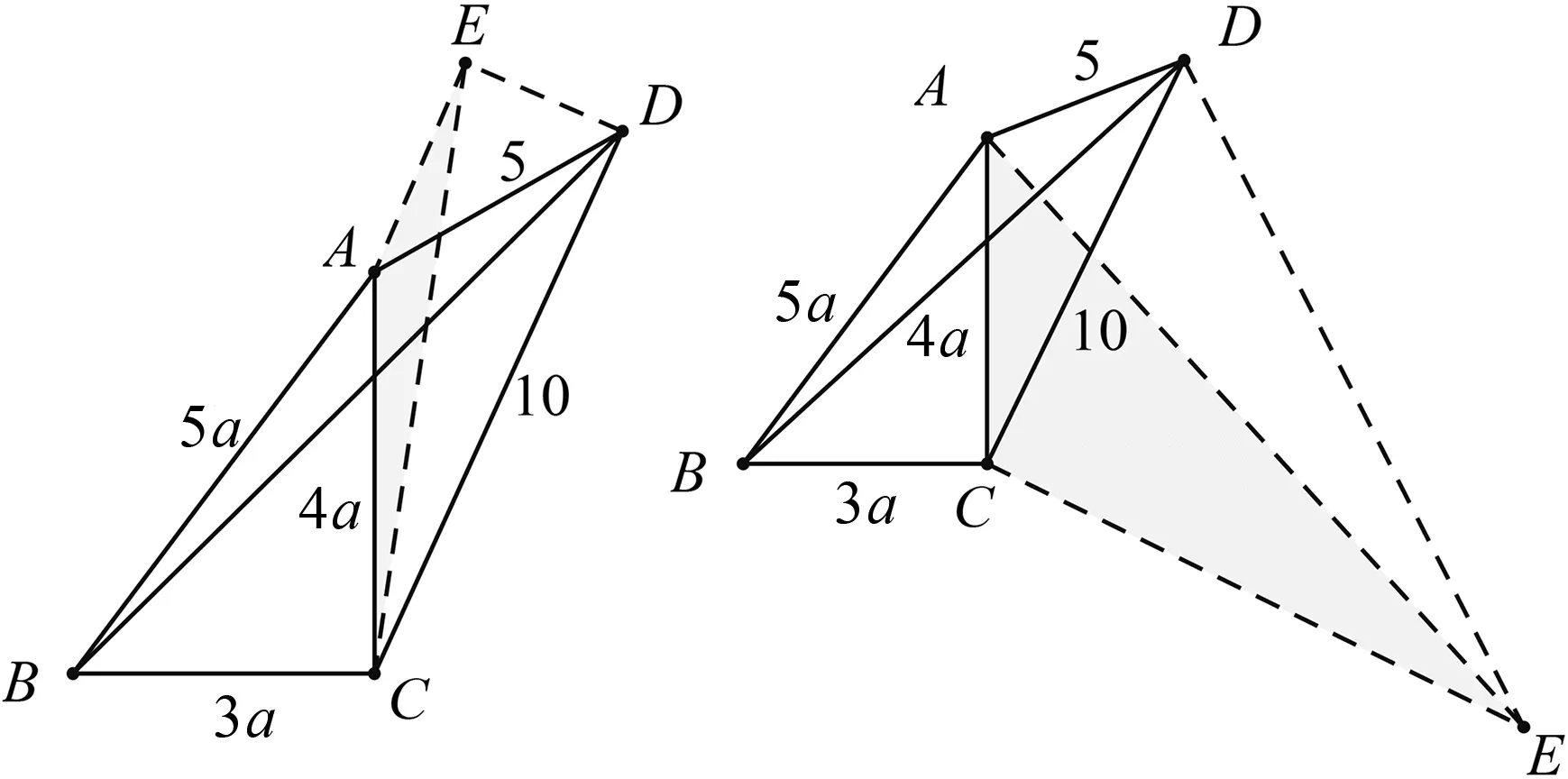
图8 图9

说明 由于已知的两条线段与待求的线段BD是共端点D的三条线段,类比上面的变式2,通过旋转构造三角形相似后,这三条线段的对应线段在同一个直角三角形上,再通过勾股定理进行计算,进而解决问题.通过以上题目的不断演变、层层递进,让学生体会解决此类问题的核心方法没有变:绕定点旋转构造相似形.
3 延伸于“对圆的旋转”
对于点的运动轨迹的问题,直线形运动和弧形运动时常是需要加以区分与辨别的.弧形运动这类题型较新颖,难度相对大一点,但其解题思路与之前两类问题相较还是“万变不离其宗”.为些,笔者以“弧形运动”为载体设置问题,不断延伸,通过图形的变化让学生感悟问题本质未变,进一步优化动态问题如何静态地解题的策略.
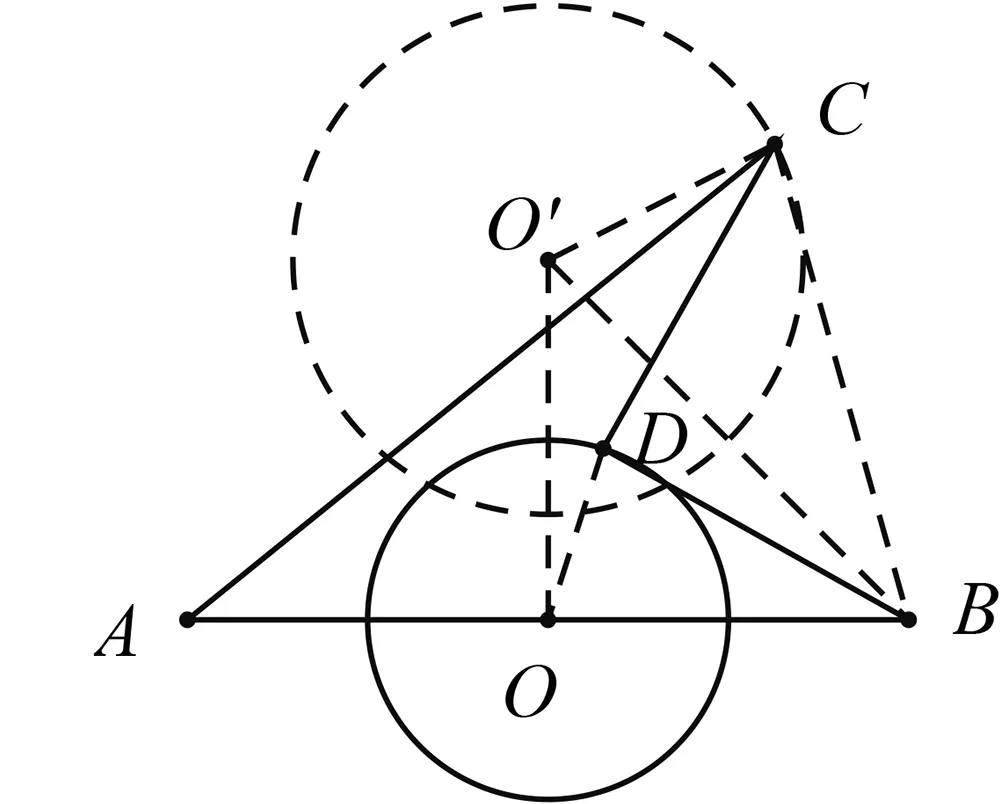
图10
例3如图10,AB=4,O为AB的中点,☉O的半径为1,点D是☉O上一动点,连结BD,将线段BD绕点D逆时针旋转90°,点B的对应点为C,连结AC.则线段AC的长的取值范围为.
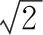
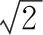

图11 图12
延伸1如图11,已知点P是正方形ABCD外一点,点O为正方形ABCD的中心,且PA=3,PB=4,则PC的最大值为,PD的最小值为,PO长的取值范围为.

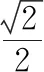
将正方形变为正六边形,还能不能通过旋转相似找到解决问题的方法呢?
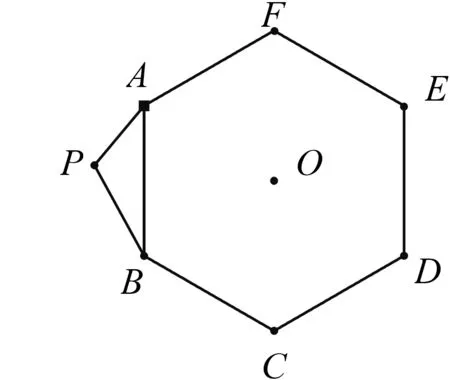
图13
延伸2如图13,已知点O是正六边形ABCDEF的中心,点P是正六边形外一点,且PA=3,PB=4,则PC的最大值为,PD的最小值为,PO长的取值范围为.
说明 延伸2虽然改变了载体,但其核心思路没有改变,可简洁归纳为:理清图中有哪些定点、动点所在的圆以及待求线段间的位置关系,通过观察、联系,确定是绕哪个定点进行旋转构造相似三角形,挖掘出新图形与特定条件之间隐藏的位置与数量关系(这里的旋转角、缩放比例很关键),进而找出新动点所在的定圆.设置这样的延伸题能让学生在进一步理清解题思路的同时,感悟出在动态的过程中始终抓“定”的数学思维.
观察上述几类题目的演变进程,我们发现解决几何问题的过程其实就是一系列的转化过程,在拓展与延伸中,通过展示数学知识发生、发展过程,有意识、有目的地引导学生从“动”中发现“定”的本质,利用其规律,进一步从“定”的本质中探究出“变”的规律,引领学生从过程中提炼方法,从方法中感悟思想,真正提高数学思维的灵活性和创造性.这样的初三专题复习正是我们日常教学中数学核心素养的落实与物化.

