面向经编机产能的预测算法设计

刘诗敬， 郗欣甫， 侯 曦， 孙以泽

(1.东华大学 机械工程学院，上海 201620; 2.中国纺织机械协会，北京 100028)

纺织企业是典型的面向订单生产的流程型制造企业，所以针对订单的预先排产是非常重要的[1]。经编机作为生产效率最高的织造机械，是国家“数控一代”项目重点发展的纺织装备之一[2]。目前，传统经编车间对织造工序的排产是由管理人员根据经验安排生产的，而不是根据科学的算法进行调度安排的，这导致生产过程出现织造时间过长、生产效率低、资源利用率低和生产成本高等问题。构建经编数字化车间是解决这些问题的有效途径，而在经编数字化车间实现科学调度属于无关并行机调度问题[3]。Garey等[4]证实这种调度问题是NP-hard完全问题。解决此类问题的前提和关键在于准确预测经编机的产能，可靠的产能预测可有效缩短加工时间，实现物料流、资金流和能量流平衡。但是，实际经编车间的经编机的构造和剩余使用寿命等均不同，操作工人在处理断纱、换针和急停等停机事件时的水平不同，这造成了经编机的异构性，以及存在各种非计划停机等模糊的影响因素，因此经编机产能的预测具有高度非线性和不确定性等特点。

虽然目前应用神经网络实现预测的相关研究已经相对成熟，但是国内外鲜有针对纺织行业产能预测的相关研究。Tedesco-Oliveira等[5]使用卷积神经网络预测棉田的产量，平均相对误差仅为8.84%，有效提高了棉花机械化收割的质量。Huynh[6]使用BP(back propogation)神经网络对纺织产品的缺陷进行有效预测，从而减少材料浪费。查刘根等[7]提出了具有双隐层的四层BP神经网络预测棉纱成纱质量，结果显示，相较于纱线断裂强力目标值，其预测值下降了8%左右。王晓晖等[8]采用遗传算法优化BP神经网络准确预测了3D增材印花产品的质量。王柳艳等[9]使用RBF(radial basis function)神经网络可靠预测了非线性的绞吸挖泥船的施工产量。么大锁等[10]基于RBF神经网络和遗传算法对注塑成型质量进行控制和预测。本文主要采用BP和RBF神经网络预测经编机产能。其中RBF神经网络能够逼近任意非线性函数并且不会陷入局部极小值，其预测能力高，适用于对高度非线性问题的求解。

1 数学建模

经编机产能预测问题是指根据可采集到的机器运转时间、故障率和机台型号等生产数据预测出经编机产能。由于输入参数和输出目标之间不存在明确的函数关系，往往需要借助神经网络算法实现对此类非线性函数的线性拟合。但是，原始的神经网络预测往往达不到精度要求，需要借助优化算法优化神经网络的输入影响参数，常用的优化算法有粒子群优化(particle swarm optimization， PSO)算法和遗传算法(genetic algorithm， GA)。此类问题可以归结为数学中的非线性函数的极值寻优问题[8]，将其抽象为数学模型如下：

(1) 设Qk=(x1，x2， …，xn)是影响经编机产能的n(n≥1)个参数，作为预测算法的输入向量。

(2) 设Tk是对应输入向量的预测产能。

(3) 设Ak为对应输入向量的实际产能。

(4) 设网络性能评价目标函数如式(1)所示。

(1)

式中：ε为迭代终止精度；m为输入样本的数目；k∈[1，m]。

(5) 设BP神经网络需要优化的权值向量和阈值向量如式(2)所示。

(2)

式中：Wi和Bi分别为BP神经网络的权值向量和阈值向量。

(6) 设RBF神经网络需要优化的中心向量、基宽向量和连接权值分别为c、σ和w。

经编机产能预测问题的数学模型网络拓扑结构图如图1所示。

2 经编机产能预测算法设计

2.1 PSO-BP算法设计

目前，BP神经网络被广泛运用于预测类问题的求解，它是根据误差反向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络[11]。BP神经网络需要借助优化算法求解权值和阈值以实现较好的预测性能。边少聪等[12]使用PSO算法优化BP神经网络，有效提高对绝缘栅双极型晶体管老化问题的预测精度。其中，PSO算法是鸟群捕食的仿生进化算法，通过群体中个体之间的协作和信息共享来寻找最优解。因此，采用PSO算法优化双隐层BP神经网络以获得高性能BP神经网络模型，其算法流程图如图2所示。

PSO-BP算法主要包括以下5个过程：

(1) 粒子种群初始化。设定粒子种群规模为20，粒子维数为2，迭代次数为500。

(2) 确定参数。设Qk为输入向量，Tk为输出向量，Ak为期望输出向量，各层之间的连接权值向量为Wi，阈值向量为Bi。

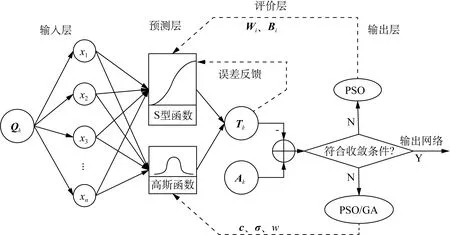
图1 经编机产能预测问题的数学模型结构拓扑图Fig.1 Mathematical model structure topology of warp knitting machine productivity prediction problem

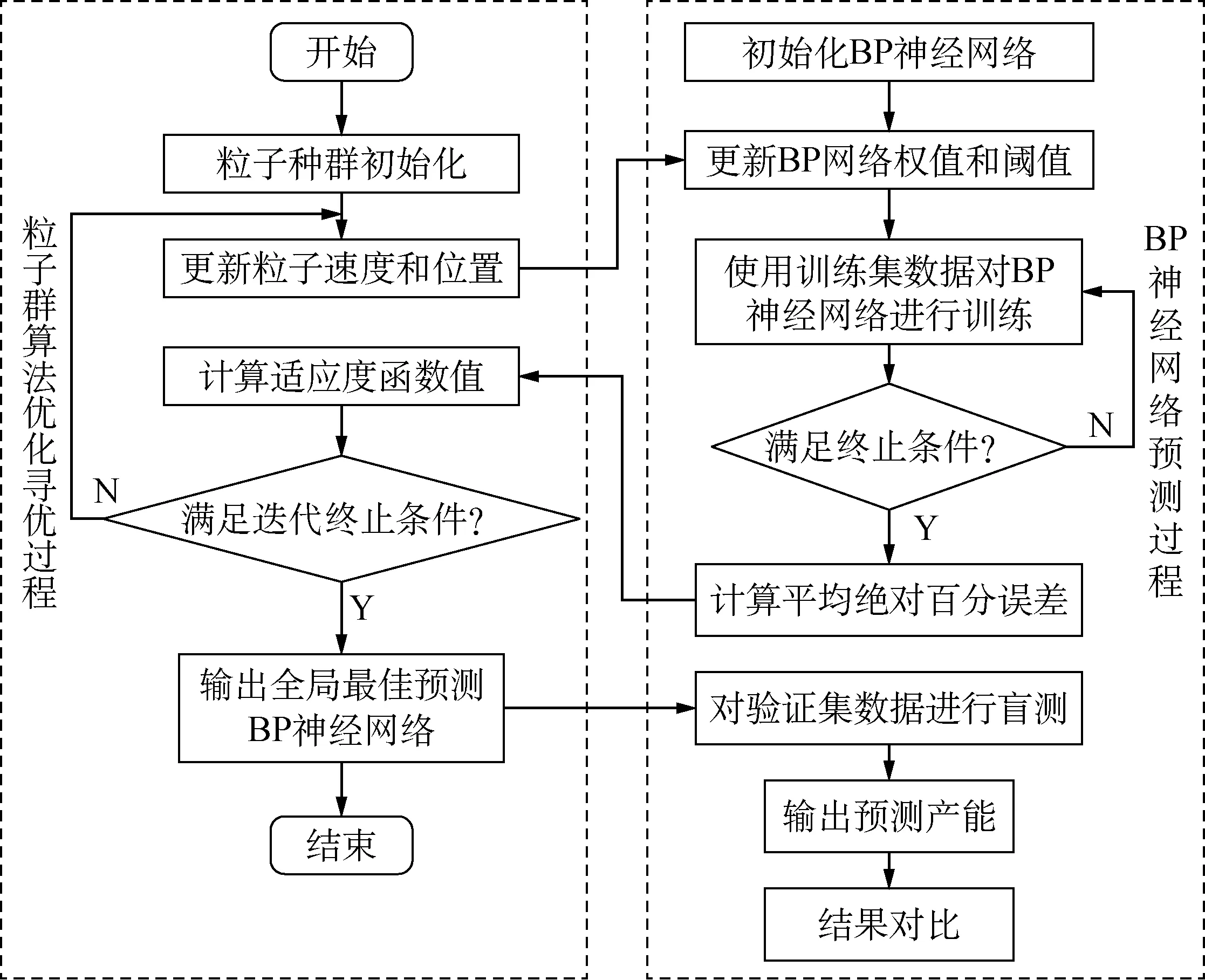
图2 PSO-BP算法流程图Fig.2 Flowchart of PSO-BP algorithm

(3) 数据归一化。为减小不同系列数据的权重影响，将数据集的各项数据归一化至[0， 1]区间。

(4) 设定激活函数。BP神经网络模型设置为双隐层，各层之间的激活函数使用对数S型函数logsig，其表达式如式(3)所示。

(3)

(5) 设定网络评价函数。网络评价函数值为训练样本的平均绝对百分误差(mean absolute percentage error， MAPE)值，表达式如式(4)所示。

(4)

PSO算法优化后得到的BP神经网络结构如图3所示。

但是，经编机产能预测问题的特殊性在于经编机的异构性导致其具有高度非线性和不确定性。BP神经网络的不足之处在于容易陷入局部极小值，且收敛速度慢。

2.2 GA-RBF算法设计

RBF神经网络是一种具有单隐层的三层前馈网络，其基本原理是将低维模式的输入数据变换到高维空间中，使得低维空间内的线性不可分问题在高维空间内线性可分。RBF神经网络能够逼近任意非线性函数，收敛速度快，且不会陷入局部极小值，相较于BP神经网络，其更适用于经编机产能预测问题的解决。但是，求解RBF网络隐节点的中心向量c、基宽向量σ和连接权值w是一个困难的问题，这导致此网络不能被广泛应用。李婧等[13]使用GA对RBF神经网络的3个关键参数进行求解，结果显示，相比较原始网络，优化后的RBF神经网络的电力系统短期预测负荷误差降低了4.7%。GA是由生物界的进化规律演化而来的随机优化搜索算法，基于适者生存进化原理，并将此原理由优化参数形成的编码串联种群中，选择一种最佳适应度函数，通过选择、交叉、变异筛选所有个体，筛选出适应能力最强的个体[14]。采用MATLAB的newrb函数生成RBF神经网络，因此对这3个参数(c、σ和w)的优化等价于优化扩散速度参数和各神经元的最大隐含节点参数。采用GA-RBF算法对经编机产能预测问题进行求解，其算法流程图如图4所示。

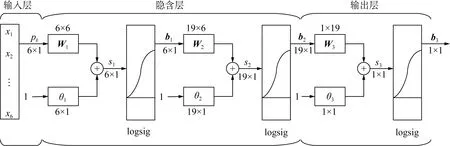
图3 双隐层BP神经网络结构图Fig.3 Structure of double hidden layer BP neural network

图4 GA-RBF算法流程图Fig.4 Flowchart of GA-RBF algorithm

GA-RBF算法设计主要包括以下7个部分：

(1) 种群初始化。根据问题的非线性程度，设初始群体规模为50，根据神经网络的输入参数有6个，设串长l为6。

(2) 染色体编码。采用浮点数编码的方式对染色体进行编码，能够更接近实际。

(3) 适应度函数设计。以网络评价目标函数MAPE值的倒数为目标函数，计算每个个体的适应度函数值，如式(5)所示。

(5)

(4) 选择运算设计。将选择算子作用于群体，把优化的个体直接遗传到下一代或者配对交叉产生新的个体遗传到下一代，选用赌轮选择法，个体被选择的概率ps(i)根据其适应度值来确定，概率函数如式(6)所示。

(6)

式中：g(i)为第i个体适应度函数值；n为种群规模。

(5) 交叉运算设计。交叉概率pc控制着交叉算子的使用频率，最佳取值区间为[0.6， 10.0]，交叉算子选用二点交叉，交叉算子设计如式(7)所示。

(7)

式中：amj和anj分别表示第m和n个染色体的第j位基因；pc取值为0.8。

(6) 变异运算设计。变异概率pm是群体保持多样性的保障，最佳取值区间为[0.005， 0.050]的pm设置为0.050，将变异算子作用于群体，对个体串的基因座上的基因值进行变动。

(7) 终止条件判断。当适应度函数值达到1×105，或者迭代次数达到了500次，则输出当前的最优解，终止计算。

使用GA优化RBF神经网络获得的最佳扩散速度为86.452，隐含层节点数为83，迭代收敛次数为240，优化时间为4.8 h。但是，GA存在局部搜索能力差和“早熟”等缺陷，不能保证算法收敛，收敛速度慢，其稳定性有待提高。

2.3 PSO-RBF算法设计

PSO算法在进化过程中同时记忆位置信息和速度信息，整个搜索更新过程是跟随当前最优解的，所以PSO算法中的粒子比GA中的进化个体以更快速度收敛于最优解。基于前两种算法提出了一种改进的混合算法，主要采用PSO算法优化RBF神经网络的中心向量c、基宽向量σ和连接权值w参数，以获得拟合能力强、收敛速度快和无局部极小值缺陷的预测算法。用优化后的RBF神经网络对验证集的数据集进行预测，以证明网络的可靠性。该预测算法主要包括PSO算法优化参数部分和RBF神经网络数据拟合部分，其算法流程图如图5所示。

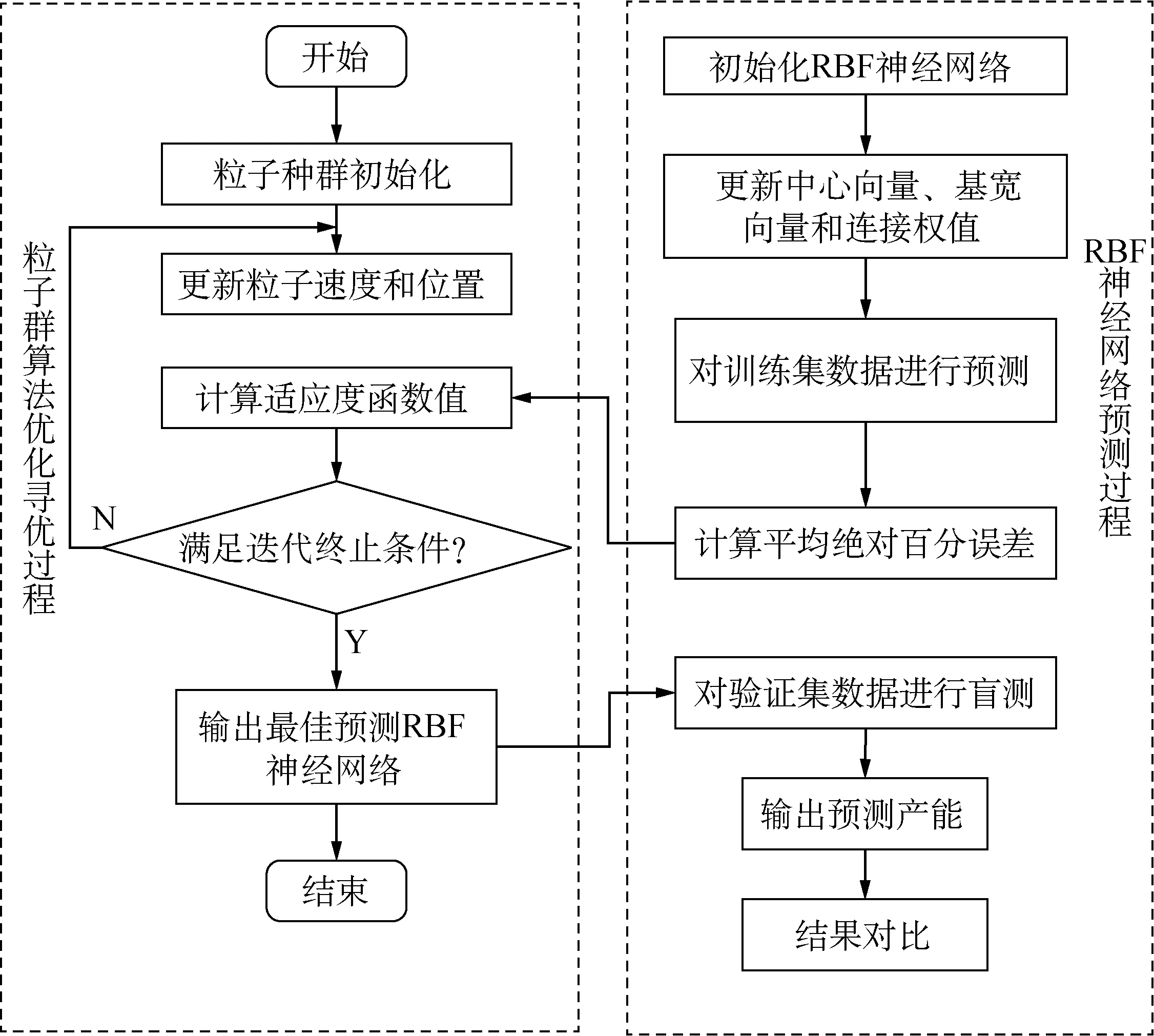
图5 PSO-RBF算法流程图Fig.5 Flowchart of PSO-RBF algorithm

首先，假设粒子群中的第i个粒子在n维空间中的位置表示为一个n维向量，该粒子的位置向量为Xi=(xi1，xi2， …，xij， …，xin)，速度向量为Vi=(vi1，vi2， …，vij， …，vin)。PSO算法优化主要包括以下5个过程：

(1) 粒子群初始化。初始粒子种群大小为20，粒子维数为2，迭代次数为500。

(2) 计算粒子适应度值。将预测产能和实际产能之间的MAPE值作为个体适应度值e。

(3) 更新个体最优位置。第i个粒子目前的最优位置记为Pbest=(pi1，pi2， …，pij， …，pin)，对每个粒子进行比较，如果其适应度值epcur优于历史最优适应度值Pbest，则用该粒子替换Pbest。

(4) 更新全局最优位置。粒子种群目前的最优位置记为Qbest=(q1，q2， …，qj， …，qn)。对每个粒子比较，如果其适应度值eqcur优于群体最优位置Qbest，则用该粒子替换Qbest。

(5) 更新粒子速度和位置。在每一次迭代过程中，粒子通过个体最优位置和群体最优位置由式(8)更新自身速度和位置。

(8)

式中：ω为惯性因子；c1和c2为学习因子；rand()为0和1之间的随机数。

RBF神经网络预测主要包括以下6个过程：

(1) 选择学习算法。在RBF神经网络学习的过程中，可以采用多种不同的学习算法，如梯度下降法、随机选取中心法、自组织学习法、K-均值聚类算法及最近邻聚类算法等[9]，通过学习可以获得决定RBF神经网络预测精度的3大参数。这里采用无监督学习中的K-均值聚类算法。

(2) 确定激活函数。采用最常用的高斯函数，因为其具有结构简单、径向对称、连续可导且解析性好的特点，其表达式如式(9)所示。

(9)

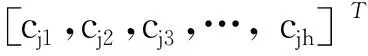
(3) 确定收敛边界条件。避免程序陷入死循环，需要设置收敛边界条件。设定迭代终止精度为1×10-5，最大迭代次数为500次，如果预测模型超过此边界条件还未收敛，则结束程序，导出当前最佳网络。

(4) 导入输入向量Qk。影响经编机产能的6维向量作为RBF神经网络的输入向量。

(5) 计算输出向量Tk。RBF神经网络学习速度极快且不需要训练，可实时输出预测产能，有效提高预测效率。

(6) 验证网络。将优化后的网络对验证集数据进行盲测，测验模型网络的可靠性。

使用PSO算法优化RBF神经网络获得的最佳扩散速度为85.217，隐含层节点数为90，迭代收敛次数为200，优化时间为3 h。

相比PSO-BP算法，PSO-RBF算法对于高度非线性曲线的拟合能力更强，而且不会陷入极小值；在大多数情况下，PSO-RBF算法相比GA-RBF算法的收敛速度更快，能够在短时间内以较大概率收敛于全局最优解。同时，PSO算法除了可以找到问题的最优解外，还会得到若干较好的次优解，因此其在调度和决策问题上可以给出多种有意义的方案。

3 试验验证

3.1 数据集选取

研究的数据集是从福建某纺织企业的经编生产数据库中提取出来的，该数据集包括10台经编机近1个月内的生产数据，每条数据记录为1个班次内单台经编机的实际产能，单条记录主要包括机台编号、故障率、运转时间和实际产能，原始数据集共有553条数据。原始数据集如表1所示。

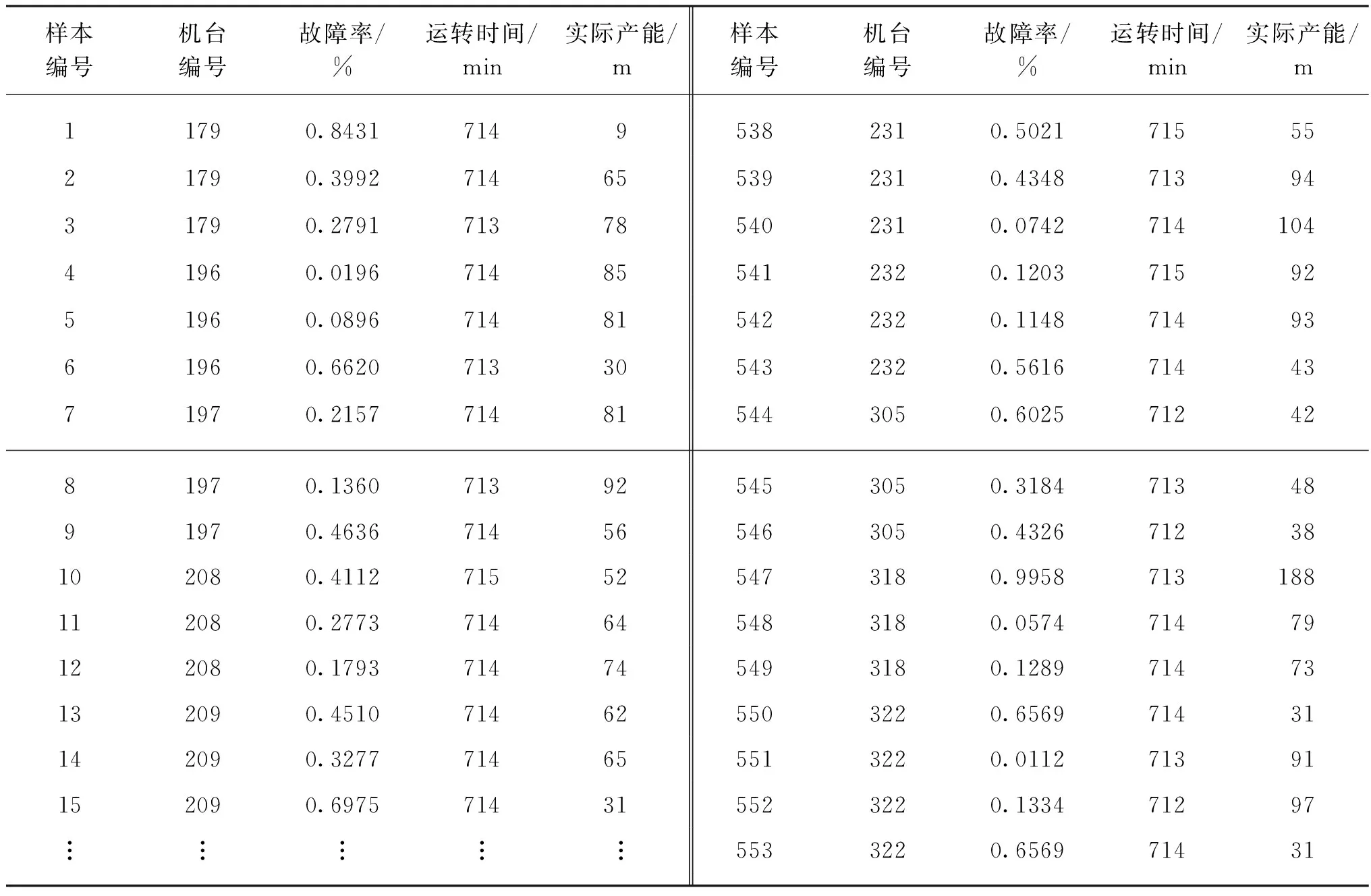
表1 经编原始产能数据Table 1 The raw productivity of wrap knitting machines

3.2 数据预处理

机台编号属于无序离散特征数据，针对此类数据，采用二进制编码方式，10台经编机共需要4位二进制数来表示，相比于独热编码值方式能够减少输入变量6个维度，可有效提升运算效率。绘制经编机产能-时间关系图如图6所示。

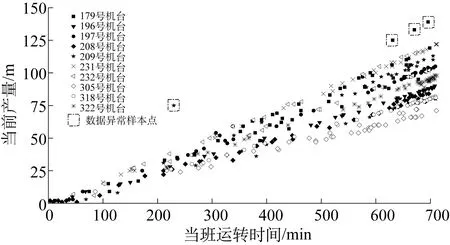
图6 经编机产能-时间关系图Fig.6 The relation between yield and runtime of wrap knitting machines

采集数据中存在一些大误差数据，需要进行数据清理，这是提高试验结果预测精度的必要措施。通过关系图6可以剔除异常的数据样本点。经过数据清理，共产生460组数据作为训练集，其中50组数据作为验证集。

3.3 试验预测与结果比较

预测的环境为2.4 GHz主频的CPU，使用MATLAB 2018a软件进行编程。使用PSO-RBF算法、GA-RBF算法和PSO-BP算法对训练数据集进行训练，并对验证数据进行盲测，预测结果对比如图7和表2所示。为了评价各模型的性能，采用MAPE值和均方根误差(root mean square error， RMSE)对预测结果进行精度评价，MAPE值可以评价一个模型的预测结果准确性，RMSE值可以评价预测值与真值之间的偏差，其表达式如式(10)所示。

(10)

式中：Yi为第i个预测值；Di为第i个真值。

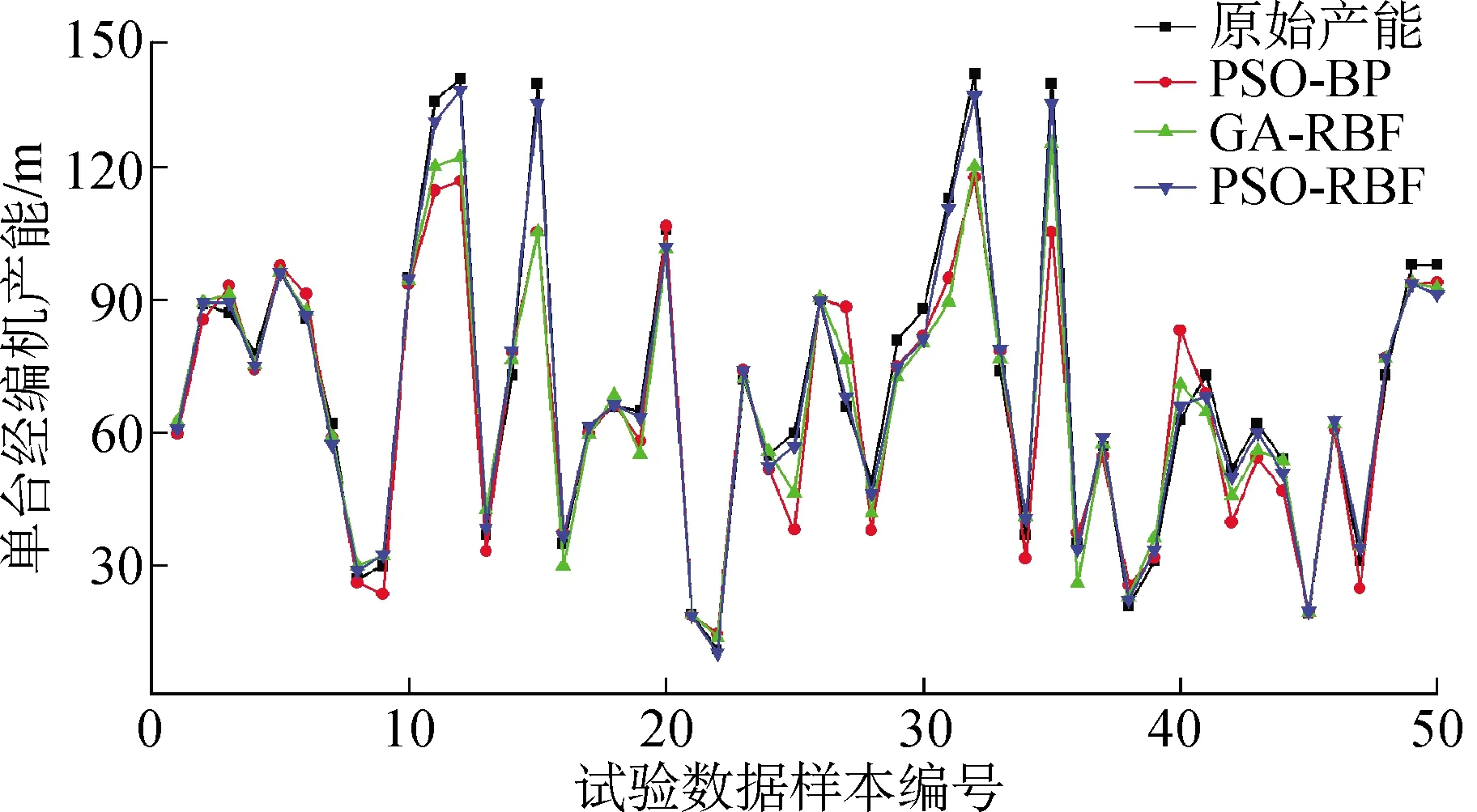
图7 3种算法的数据预测结果对比图Fig.7 Comparison of data prediction results of three algorithms

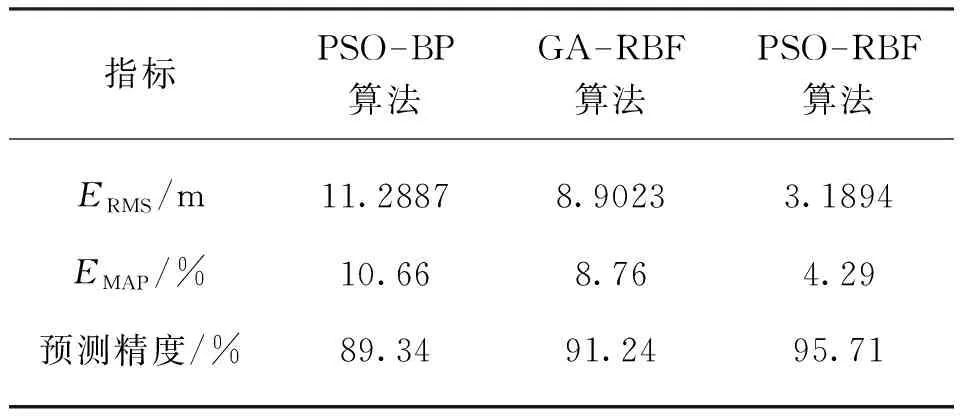
表2 3种模型预测结果对比表Table 2 The comparison of prediction results of three algorithms

由图7和表2可知：对于此类非线性及不确定性因素较多的预测类问题，RBF神经网络比BP神经网络的预测精度更高，数据拟合能力更强；PSO算法和GA都能有效提高预测精度，但是PSO算法具有较好的全局精度和更快的收敛速度，而GA的预测较为不稳定；PSO-RBF算法的预测精度达到了95.71%，同时其RMSE值和MAPE值是3种预测算法中最小的。

4 结 语

针对具有高度非线性和不确定性的经编机产能预测问题，本文设计了PSO-BP、 GA-RBF和PSO-RBF 3种算法，其中PSO-RBF算法性能显著，具有全局预测能力强、收敛速度快和单体预测能力稳定等优点。试验结果表明，PSO-RBF算法对经编机的产能预测精准，全局预测精度达到了95.71%。该结果对实际生产具有指导意义，能够有效推进纺织数字化车间生产的科学调度，同时证明了PSO算法在优化RBF神经网络的方面具有可行性和可靠性，对RBF神经网络的推广具有一定意义。本文不足之处在于PSO算法优化RBF神经网络仍然需要花费较多时间，因此，减少优化时间将是进一步研究的内容。