柔性三角梁约束微纳测头的变刚度特性分析

李保坤， 程新华， 韩迎鸽

(安徽理工大学a.机械工程学院；b.电气与信息工程学院，安徽 淮南232001)

随着微纳米加工技术的不断发展，工件制造日趋微型化和精密化，各种微电子机械系统(micro electro mechanical system， MEMS)器件相继出现，这些微工件制造成本低廉，同时具有集成化和多功能化等优点，制造产品被广泛应用于航空航天、精密机械、生物医学等领域[1-3]。在MEMS器件的制造过程中，需要测量这些微工件的表面几何参数，然而传统精密测量仪器的测量精度仅有微米级，难以实现纳米级别的分辨率，亟需研究具有优良性能的微纳坐标测量机以保证工件表面质量[4-6]。测头是测量机的核心部件[7]，其性能是否优良直接决定测量机的整体性能优劣，因此，国内外许多研究机构相继开始研究新型微纳测头。

刚度是微纳测头的重要属性，目前多数接触式测头约束支撑机构的刚度不可调。若微纳测头刚度过大，在测量时极易划伤工件表面；若测头刚度过小，容易造成测头动态响应性能差、谐振频率低和误触发等。因此，研究具有变刚度性能的约束支撑机构以适应测量过程和被测工件的改变，对优化测头的测量力、稳健性、工艺性、测量精度和动态特性等具有重要意义[8-9]。

鉴于测头约束支撑机构刚度固定的诸多不利影响，Bonello等[10]提出通过改变约束梁的有效长度改变测头的支撑刚度。文献[11-13]基于应力刚化原理，通过对支撑梁约束端施加轴向载荷来改变约束支撑梁的横向刚度。Kim等[14]提出通过施加额外载荷放大载荷作用位移来调节刚度。Alblalaihid等[15]通过施加预应力的方式提出一种基于三根梁约束支撑的变刚度微纳测头，但未能给出精确的理论刚度模型。

本文利用梁轴向受载以改变约束梁支撑刚度这一基本原理，构造出一种三角梁结构型式的变刚度微纳测头。在测量过程中，通过控制压电驱动力大小进而改变测头约束支撑机构的整体刚度，以满足不同的测量过程和测量对象。当测头接触被测工件时，要求测头约束支撑机构具有较小的刚度，避免划伤被测工件表面，此时压电叠堆驱动器输出压电驱动力减小，约束支撑机构整体刚度减小，即将压电叠堆器输出力通过柔顺机构传递至约束支撑梁末端，测头约束支撑机构的横向刚度随支撑梁轴向压力增大而减小，因此测头约束支撑机构的整体刚度减小。当测头趋近或远离被测工件时，要求测头约束支撑机构具有较大的刚度避免误触发，此时压电叠堆驱动器停止输出压电驱动力，测头恢复初始刚度。因此，测头约束支撑机构可通过控制压电驱动力大小完成变刚度过程。应用最小势能原理建立测头约束支撑机构的刚度模型，利用有限元分析工具验证了理论刚度模型的正确性和该类型测头约束支撑机构变刚度调节的可行性。

1 变刚度约束微纳测头构造

压电驱动三角梁结构变刚度微纳测头整体构型如图1所示，其由测球、测杆、中心体、约束支撑梁、H型柔性机构、压电叠堆驱动器和柔性铰链等部分组成。

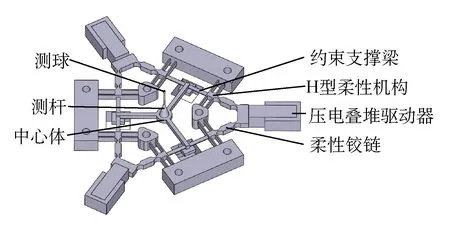
图1 微纳测头结构Fig.1 Structure of micro-nano probe

微纳测头变刚度原理如图2所示，当需要减小约束机构的支撑刚度时，压电驱动器输出驱动力。图2中：Ai及Bi(i=1， 2，...，6)处为柔性铰链，易知铰链两端受力为一对平衡力；由伪刚体模型[16]可知，压电驱动器在驱动过程中，可将AiBi段视为二力杆，压电驱动力将沿AiBi连线的方向并通过H型梁作用于约束支撑梁末端，并始终沿支撑梁轴线方向，使得在3个相同压电驱动力作用下，中心体受约束支撑梁作用力均匀。此时，在轴向力的挤压下，约束支撑梁横向刚度减小，进而减小整个约束支撑机构的支撑刚度。若压电驱动器停止输出驱动力，约束支撑梁及整体支撑机构的刚度恢复初始状态。因此，测头在使用过程中可通过控制压电驱动器输出作用力大小实现约束支撑机构的变刚度过程。

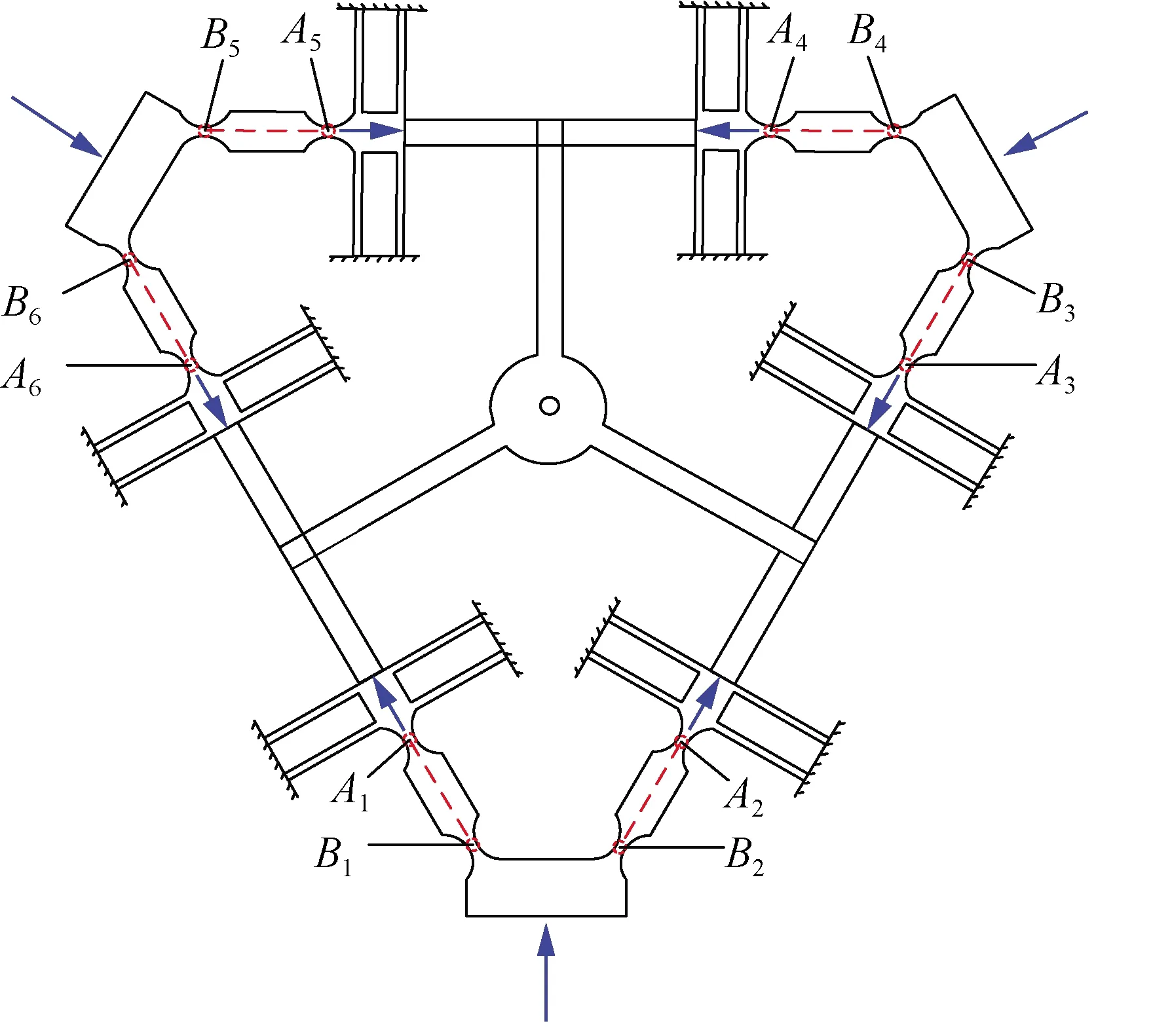
图2 微纳测头变刚度原理Fig.2 Variable stiffness theory of micro-nano probe

测球选用红宝石，测杆选用碳化钨，中心体选用钛合金，约束支撑梁选用铍青铜，柔性铰链选择弹簧钢作为结构材料。微纳测头材料属性[17-18]如表1所示。

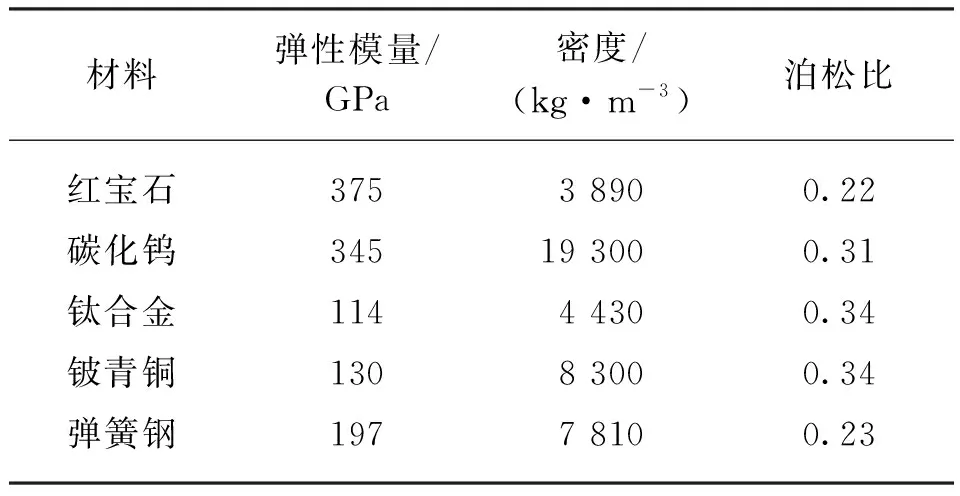
表1 微纳测头材料属性Table 1 Material property of the micro-nano probe

测头的测量工作过程见图3，主要分为3个阶段[19]：(1)测头快速趋近工件；(2)测头与工件相接触，完成工件表面位置信号的采集；(3)测量完成，测头与工件相互分离，测头恢复初始位置。

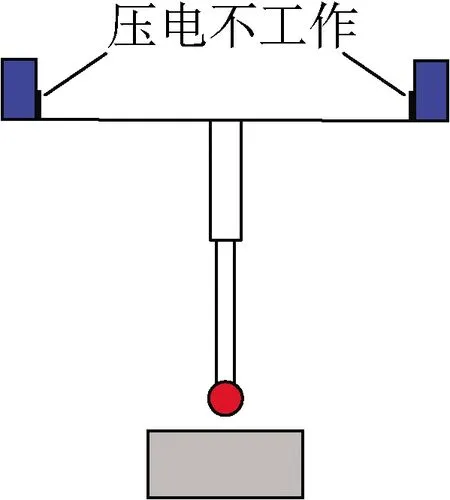
(a) 测头趋近

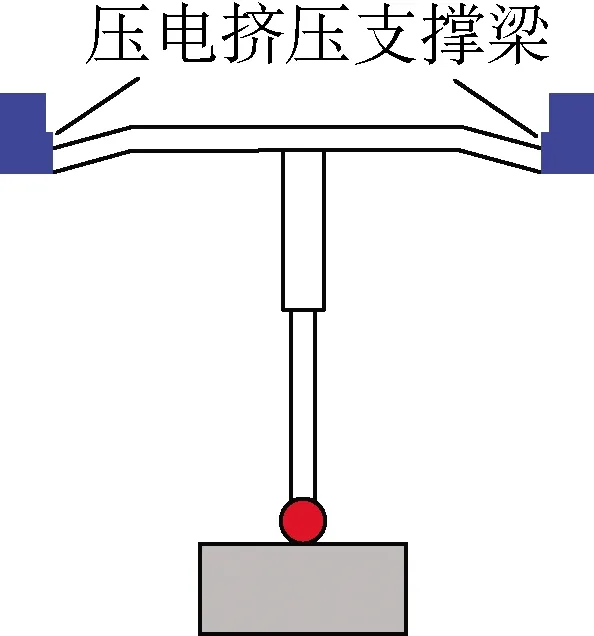
(b) 触碰工作

(c) 测头远离

基于上述测头的测量工作过程：当测头快速趋近工件时，为保证测头系统的稳定性，避免测头因惯性力产生误触发，提高测头的动态响应特性，此时无压电驱动力，测头约束支撑机构具有较高的刚度[20]；当测头与工件接触时，由于工件尺寸较小，为避免测头对工件表面造成划伤或者破坏，压电驱动器输出作用力，测头约束支撑机构具有较低的刚度；当测头完成测量工作离开工件表面时，为克服工件之间的范德华力[21]，此时压电驱动器停止输出作用力，测头约束支撑机构需要具有较高的刚度。

2 微纳测头理论刚度模型

测头约束支撑机构(即悬挂机构)的刚度大小计算方法主要有数值解法和理论建模法。其中，数值解法的相关计算方法也较为成熟，例如，利用有限元方法，根据支撑机构的结构参数和材料特性，可精确得到其支撑刚度。然而，数值解法难以得到支撑机构的刚度计算解析表达式，使得在实际使用过程中，由于测量过程及测量对象的改变，较难以实时预测压电驱动力大小并对支撑机构的刚度大小进行实时控制。理论建模法则通过相关数学及物理模型构建约束支撑机构的刚度解析表达式，可对约束支撑机构的刚度值随压电驱动力大小改变情况进行实时预测，从而对约束支撑机构的变刚度控制提供可能。

根据上述测量原理，微纳测头的刚度主要由测头约束支撑机构整体刚度决定，因此需要构建该类型微纳测头约束支撑机构的理论刚度模型，为实现其变刚度控制奠定理论基础。由于约束支撑梁长度远大于梁厚度，即为细长梁，可忽略剪切变形影响，故可基于欧拉-伯努利梁模型对其刚度进行建模[22]。假设约束支撑梁变形在线弹性变形范围内，利用最小势能原理进行求解。

2.1 垂直刚度建模

微纳测头约束支撑机构结构参数如图4所示。为便于分析，建立全局固定坐标系，坐标原点与中心体中心层圆心初始位置重合，x轴正向沿中心体其中一根连接轴的轴向方向，z轴正向竖直向下，y轴方向由右手法则确定。其中：中心体几何中心到约束梁中心线距离为wi，中心体宽度为wd；约束支撑梁长度为l，宽度为wb，厚度(z向)为tb；测杆末端至坐标系原点距离为ls。

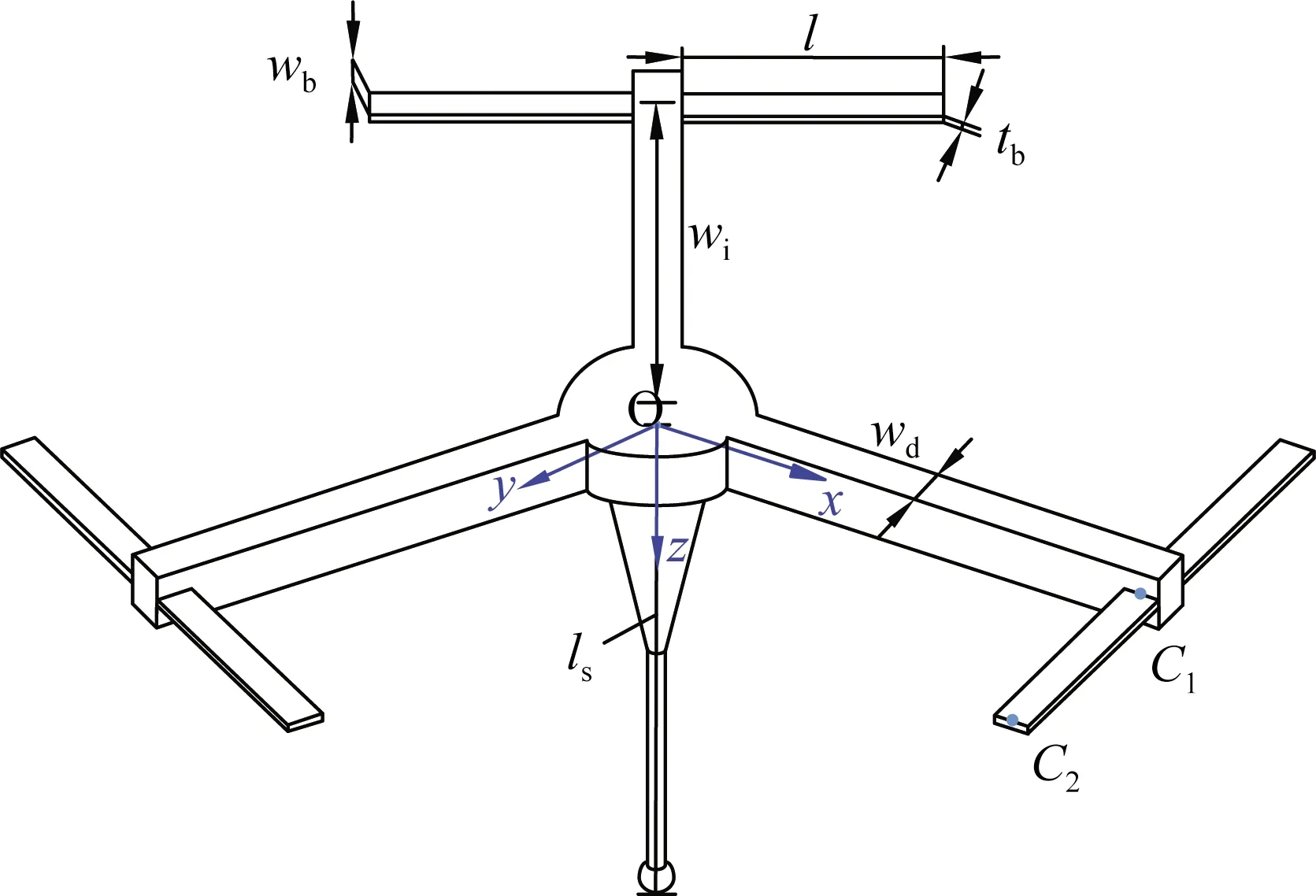
图4 微纳测头约束支撑机构结构参数Fig.4 Structure parameters of supporting mechanism of the micro-nano probe

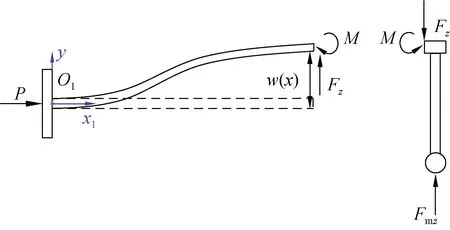
图5 单根约束支撑梁及测头受z轴向测量力力学分析Fig.5 Force analysis of one supporting beam and the probe applied by z-directional force

选取C1-C2段约束支撑梁进行受力分析并进行刚度建模，由于结构对称性，其他约束支撑梁应具有相同的垂直刚度(z轴向刚度)。建立如图5所示的局部坐标系，当微纳测头受到垂直方向(z轴向)测量力Fmz作用时，每根约束支撑梁受相同的z轴向测量分力Fz，即Fmz=6Fz。约束支撑梁与柔顺机构和中心体之间的连接均可分别视为对支撑梁的固定约束。

约束支撑梁的变刚度过程主要发生弯曲变形和轴向挤压变形，因此建立约束支撑梁弯曲试函数[23]，如式(1)所示。

w(x)=a1x2+a2x3

(1)

式中：a1、a2为待定系数，其值可根据约束支撑梁边界条件和总势能泛函求得。

应用最小势能原理，梁的位移边界条件为

(2)

计算边界条件得：

(3)

约束支撑梁的总势能泛函为

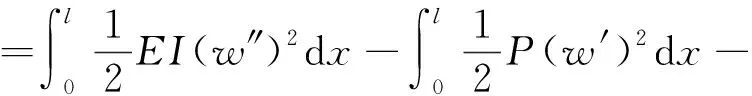
Fzw(l)-Mw′(l)

(4)

式中：E为约束支撑梁弹性模量；M为中心体对约束支撑梁作用弯矩；P为支撑梁约束端所受轴向压力；I为截面惯性矩，其大小如式(5)所示。

(5)

联立式(1)～(5)得：

(6)

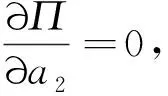
(7)

2.2 横向刚度建模

微纳测头横向受力如图6所示，每根约束支撑梁两端均为固定约束。当微纳测头受到横向测量力作用时，测头约束支撑机构主要发生弯曲和扭转变形，设测头弯曲角度和扭转角度分别为θ和α。测头约束支撑机构的横向刚度Ky可由柔性梁弯曲变形对测头及中心体造成的转动刚度(简称弯曲刚度，记为Kb，下同)和柔性梁扭转变形对测头及中心体造成的转动刚度(简称扭转刚度，记为Kt，下同)相加得到，即有：

Ky=Kb+Kt

(8)

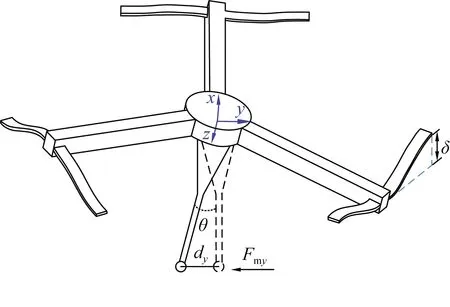
图6 微纳测头横向受力图Fig.6 Lateral force diagram of the micro-nano probe

2.2.1 弯曲刚度计算

微纳测头横向弯矩示意如图7所示。由于结构对称性，以发生弯曲变形的C3-C4段约束支撑梁为例，计算约束支撑梁对中心体的弯矩，如图8所示。

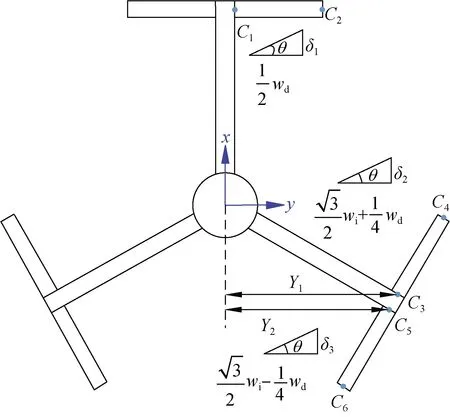
图7 微纳测头横向弯矩示意图Fig.7 Lateral moment diagram of the micro-nano probe

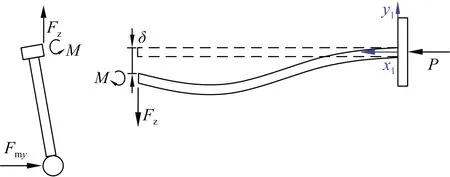
图8 约束支撑梁在横向测量力作用下的弯曲变形图Fig.8 Bending deformation diagram when the supporting beam is applied by the lateral force

由于测头受横向测量力时，约束支撑梁均为细长梁，且梁受载荷情况与边界条件一致，由式(7)得到单根梁受轴压和弯矩作用下的刚度Kbe如式(9)所示。

(9)

约束支撑机构弯矩平衡示意图如图9所示，其中Fbi(i=1， 2， 3)为约束支撑梁对中心体的反馈力。

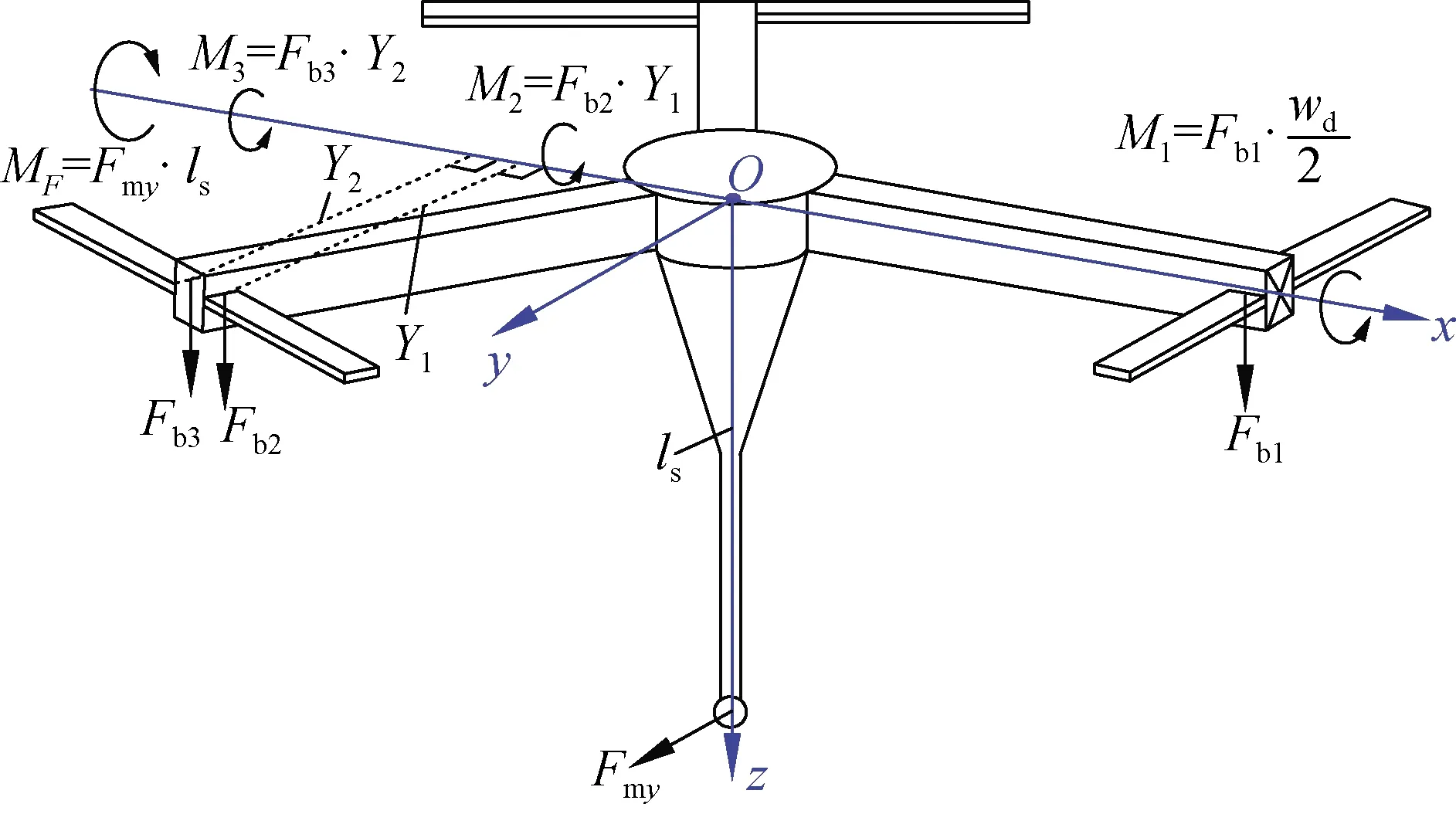
图9 约束支撑机构弯矩平衡示意图Fig.9 Moment balance diagram of the supporting mechanism

对于C1-C2段约束支撑梁，C1处挠度为

(10)

C1所受弯矩M1

(11)

对于C3-C4段约束支撑梁，C3处力臂为

(12)

C3处的挠度为

(13)

C3所受弯矩为

(14)

对于C5-C6段约束支撑梁，C5处力臂为

(15)

C5处的挠度为

(16)

C5所受弯矩为

Kbetanθ

(17)

由于约束梁所受弯矩M1、M2、M3将作用于中心体上，得到中心体力矩平衡方程如式(18)所示。

Fmyls=2M1+2M2+2M3

(18)

测头位移与偏转角存在如式(19)所示的三角函数关系，由于测头受横向载荷时偏转角较小，故tanθ≈θ。

dy=lstanθ≈lsθ

(19)

联立式(11)、(14)、(17)、(18)及(19)得到弯曲刚度Kb，如式(20)所示。

(20)

2.2.2 扭转刚度计算

图7中C3-C4段约束支撑梁受扭转作用发生变形如图10所示。

如图10(a)所示，设约束支撑梁绕局部坐标系x2y2z2中x2轴的扭转力矩为T，沿x2轴的轴向压力为P。这里选取前两项三角级数作为转角函数的试函数，如式(2)所示。

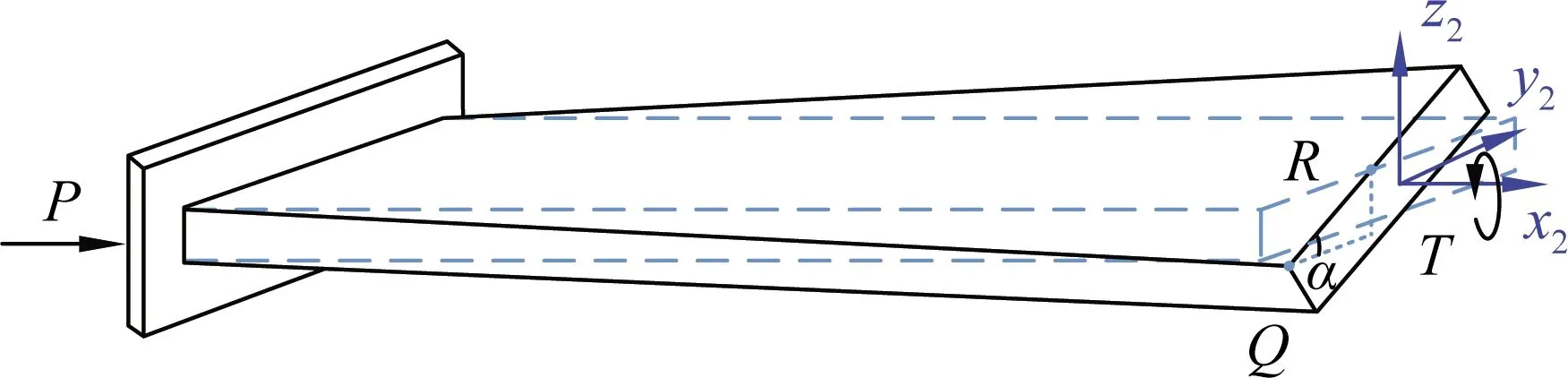
(a) 扭转变形

(b) 轴向微元变形

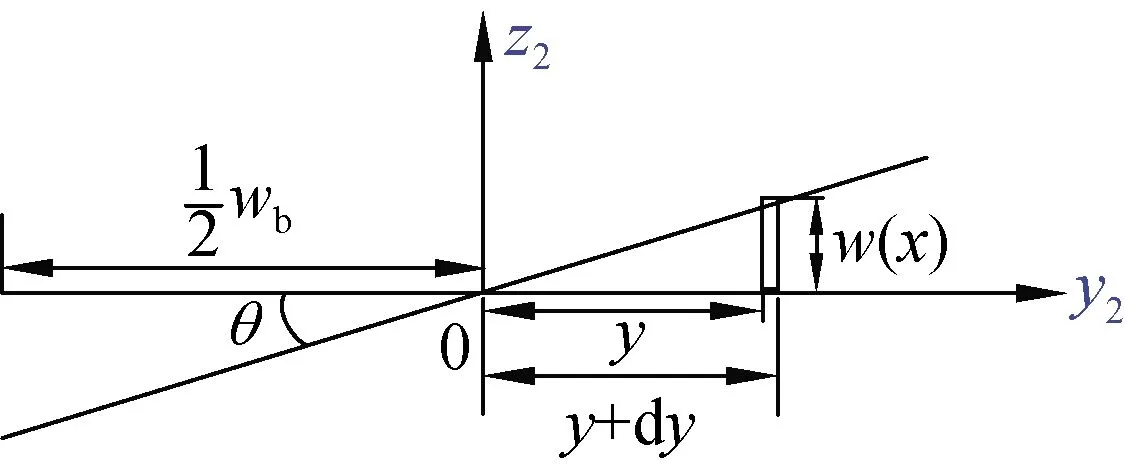
(c) 扭切截面变形

(21)

式中：c1、c3为待定系数。

根据最小势能原理，约束支撑梁的转角函数边界条件[24]为

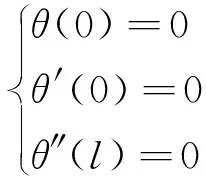
(22)

根据图10(b)、(c)得到约束梁的微元位移函数为

w(x)=θ(x)y

(23)

约束支撑梁在轴向压力和扭转力矩作用下的总势能泛函为

Tθ(l)

(24)

式中：G为剪切模量；J为矩形截面惯性矩。

由最小势能原理可知，任意满足位移边界条件的试函数中，如果试函数范围内没有精确的包含真实位移函数，那么在加权残值最小的条件下，对平衡方程和力的边界条件求得最佳逼近试函数的一组解，使得总势能泛函为最小值。因此，对约束支撑梁总势能泛函取极小值，将式(21)～(23)代入式(24)，令

(25)

由式(21)～(25)得

(26)

根据式(21)和(26)得到单根约束支撑梁绕自身轴心线的扭转刚度Ket，如式(27)所示。

(27)

测头与支撑梁扭矩平衡示意如图11所示。

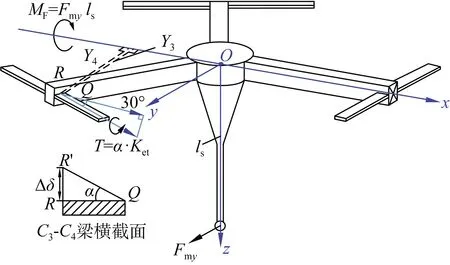
图11 测头与支撑梁扭矩平衡示意图Fig.11 Torsion balance diagram of the probe and supporting mechanism

对于C3-C4段梁Q处的相对x轴转动的旋转半径为

(28)

Q处相对x轴转动的挠度为

(29)

对于C3-C4段梁R处相对x轴转动的旋转半径为

(30)

R处相对x轴转动的挠度为

(31)

由于C3-C4段约束支撑梁受扭转作用，该梁与中心体连接的末端Q处与R处相对x轴转动的挠度差为

(32)

C3-C4段梁扭转角α为

(33)

由于测头受横向载荷时偏转角较小，故偏角sinα≈α， tanθ≈θ，因此式(33)变为

(34)

受扭转和轴压作用的C3-C4段梁的扭矩T=αKet， 即有

(35)

由于结构对称性，根据中心体力矩平衡方程可得

Fmyls=4Tcos 30°

(36)

联立式(19)、(35)、(36)得到扭转刚度Kt如式(37)所示。

(37)

令Kz=Ky，得测头刚度各向同性时所需的压电驱动力Piso为

(38)

而

P=Piso

(39)

将式(39)代入式(7)，即可求得各向同性刚度的大小。当压电驱动器输出作用力如式(38)所示，测头约束支撑机构处于刚度各向同性状态，有利于减小测量的不确定度[25]。

3 数值举证与仿真试验验证

三角梁微纳测头尺寸参数如表2所示，为分析上述刚度模型的正确性，利用有限元工具加以验证。

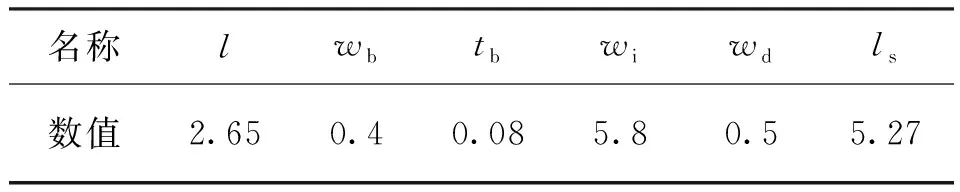
表2 微纳测头结构参数Table 2 Structure parameters of micro-nano probe mm

根据表2所示的微纳测头结构参数，建立测头约束支撑机构的仿真模型并进行有限元仿真，在支撑梁末端分别施加固定约束，对测球表面分别施加z轴向和横向均为0.1 mN的测量力，微纳测头在z轴向和横向的位移云图如图12和13所示。

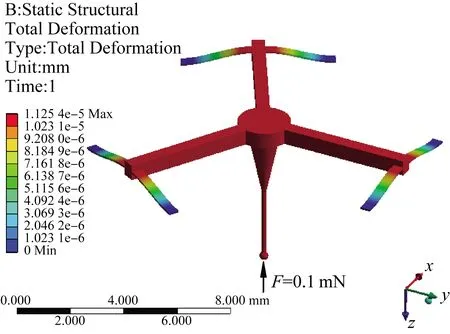
图12 当P=0 N和z轴向力为0.1 mN时的测头位移Fig.12 The displacement of the probe when P=0 N and z-directional probe force is 0.1 mN

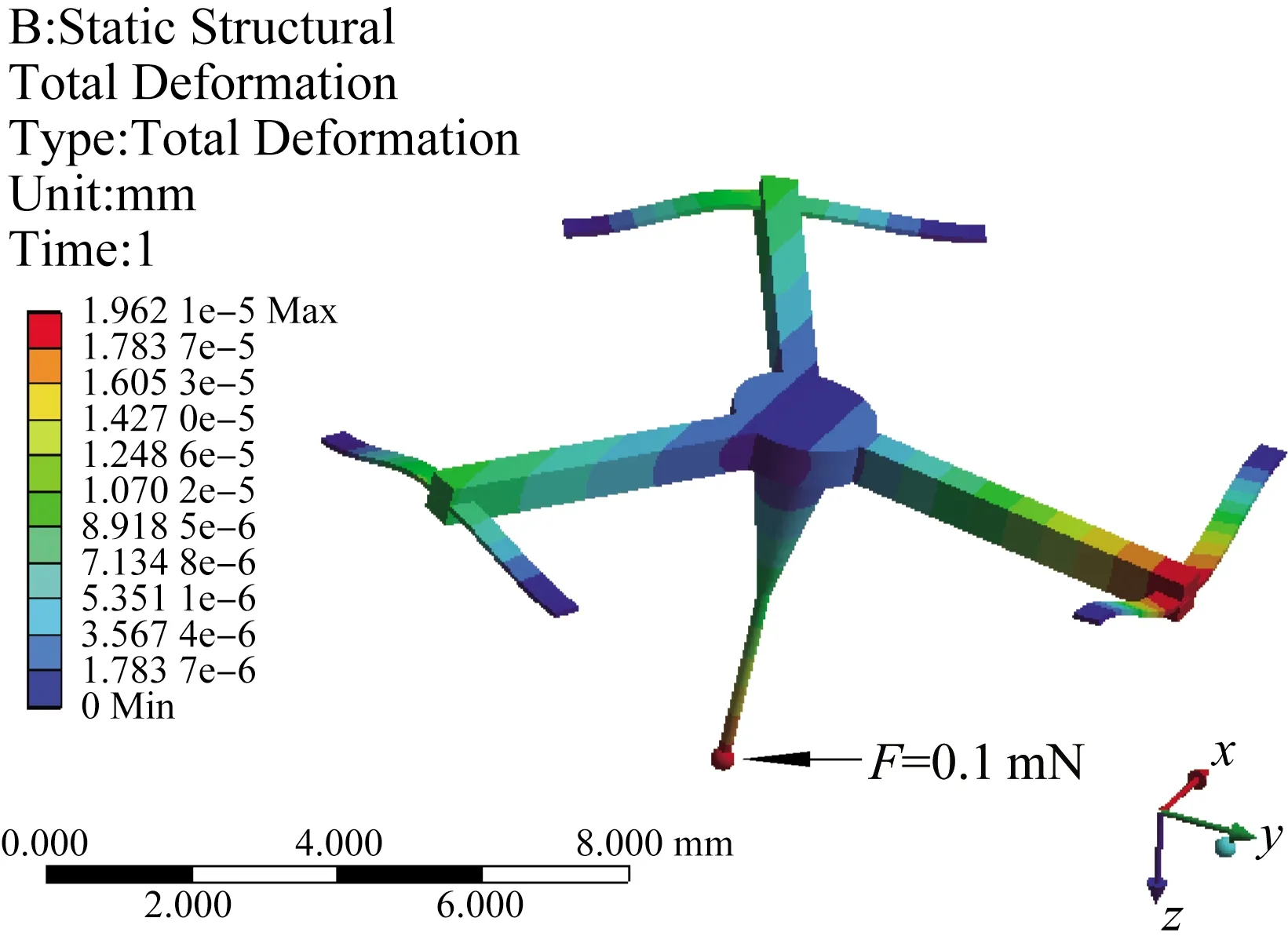
图13 当P=0 N和横向力为0.1 mN时的测头位移Fig.13 The displacement of the probe when P=0 N and lateral probe force is 0.1 mN

由图12和13可知，当微纳测头不受压电驱动力作用时，即P=0 N时，测头的初始垂直刚度和横向刚度分别为8.734 8和5.172 2 mN/μm。

由于压电驱动力对应于支撑梁约束端所受不同轴向压力，利用式(7)、(8)和有限元工具分别获得测头约束支撑机构在支撑梁约束端所受不同轴向压力情况下的垂直刚度、横向刚度的理论值和仿真值，如图14所示。

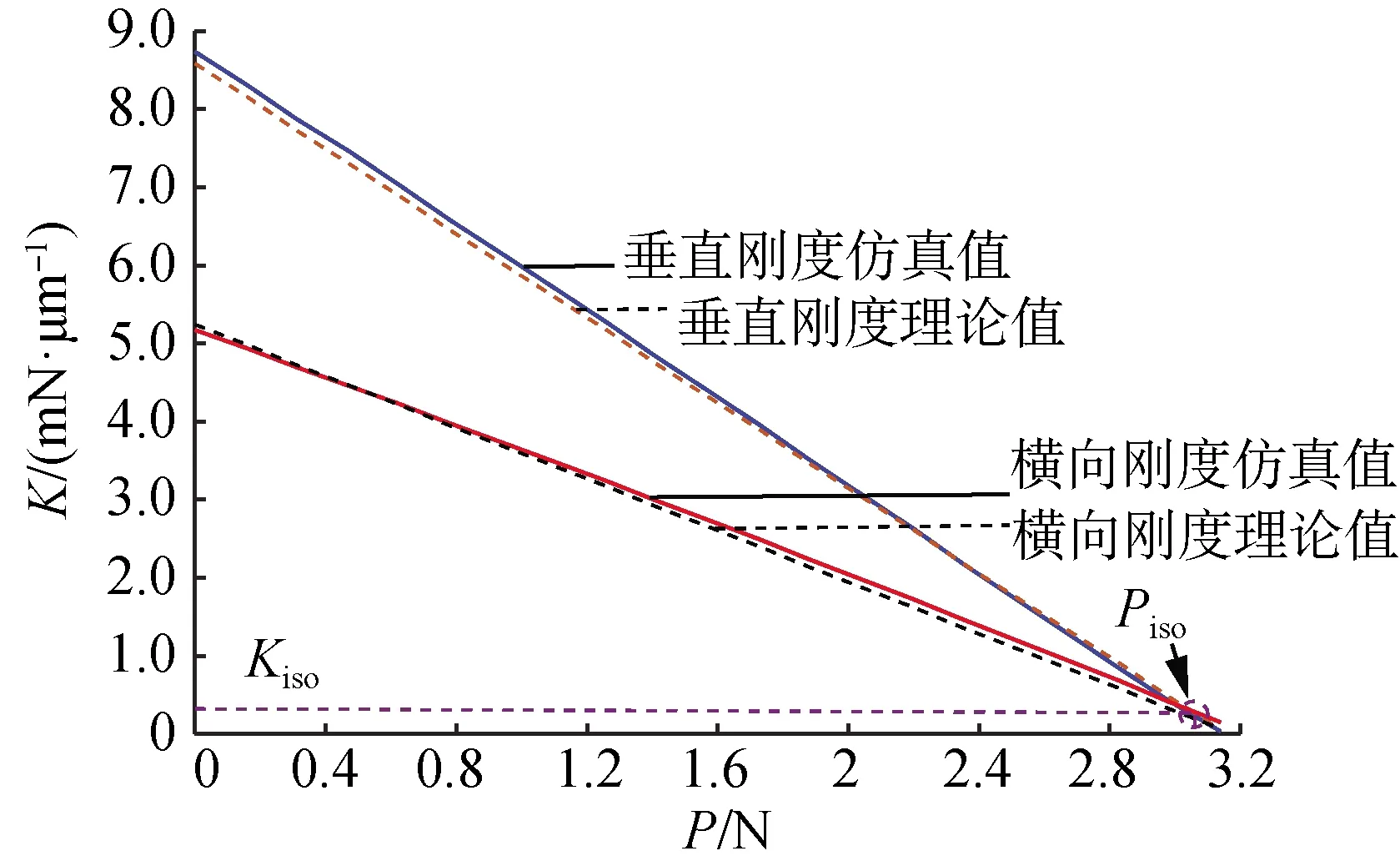
图14 测头刚度随支撑梁约束端受轴向压力的变化Fig.14 Probe stiffness variation versus the force applied on the restrained end of the supporting beam

由图14可知，当压电驱动力的范围为0≤P≤Piso时，测头刚度随着支撑梁约束端所受轴向压力的增大而减小，测头支撑刚度与支撑梁约束端所受轴向压力呈线性关系，支撑梁约束端所受轴向压力越大，约束支撑刚度越小，而压电驱动力通过柔顺机构传递至支撑梁约束端，直接影响约束端所受轴向压力大小，故可通过控制压电输出力来控制测头的约束支撑刚度。当Piso≤P≤Pcry(临界载荷)时，此时测头极易在任意微小扰动下发生弯曲失稳，因此，对测头施加的压电驱动力应当小于Pcry，其值可通过令式(7)或(8)为0求得。

采用平均相对误差公式计算测头约束支撑刚度的理论值和仿真值的平均相对误差，如式(40)所示。

(40)

式中：S为平均相对误差；Xj为仿真值；Yj为理论值；n为取值点数。

由式(7)、(8)分别计算得到垂直刚度Kz与横向刚度Ky，结合仿真结果，利用式(40)分别计算两种刚度的理论值和仿真值之间的平均相对误差分别为4.40%和5.41%。

将表2微纳测头约束支撑机构的结构参数分别代入式(7)或(8)计算得到约束支撑机构发生屈曲时所需的压电驱动力Pcry的理论值为3.16 N，而约束支撑机构刚度各向同性时所需的理论压电驱动力值Piso为3.05 N。因此，对约束梁施加3.05 N的压电驱动力使得测头约束支撑机构达到刚度各向同性，不会发生约束梁失效及屈曲的现象。

根据有限元分析工具得到测头刚度各向同性时所需的压电驱动力Piso的仿真值为2.98 N。因此，测头达到刚度各向同性时所需压电驱动力Piso的理论值与仿真值相对误差为2.3%。在约束梁末端分别施加P=2.98 N的压电驱动力，对测球表面分别施加z轴向和横向均为0.1 mN的测量力，微纳测头在z轴向和横向的位移云图如图15和16所示。

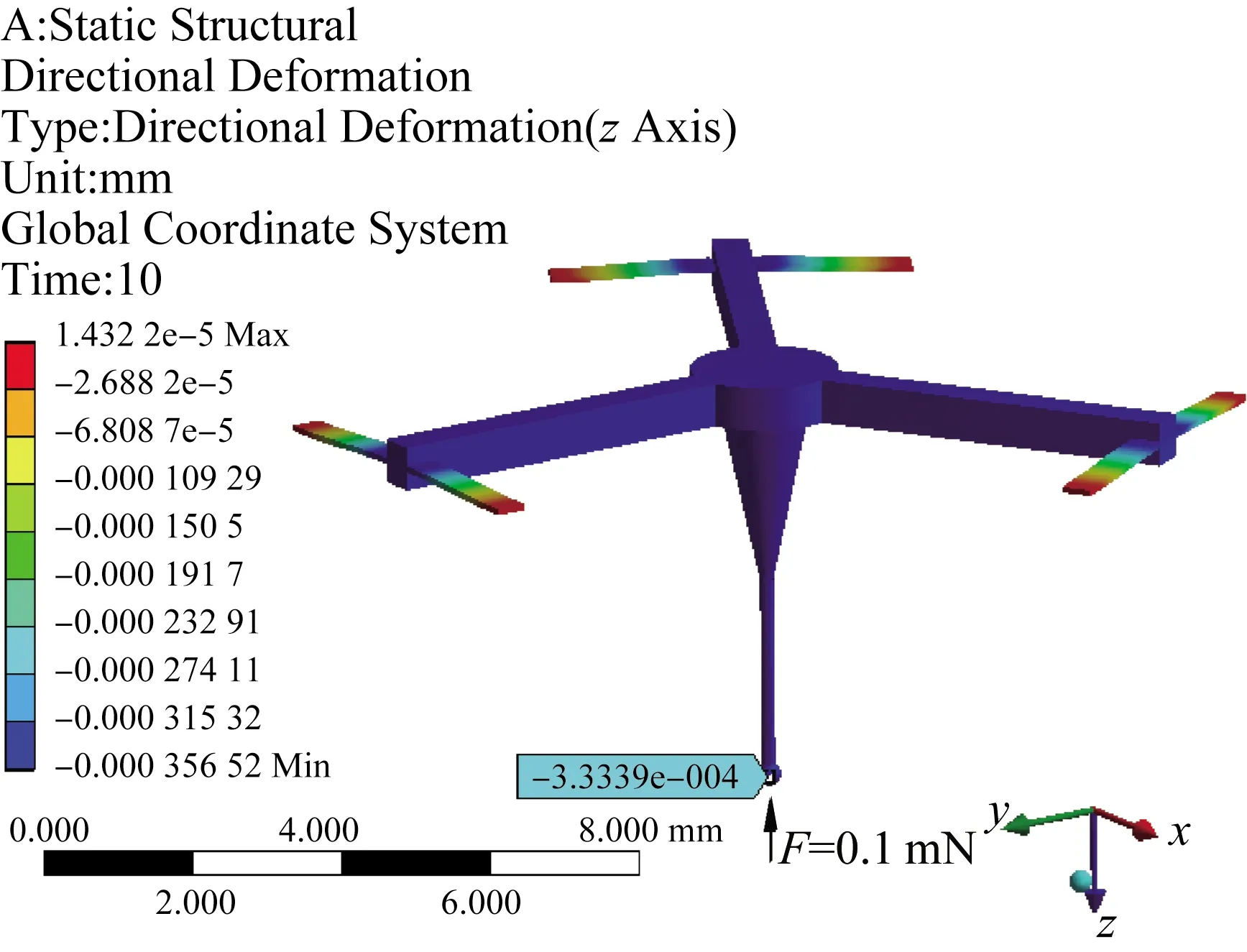
图15 当P=2.98 N和z轴向力为0.1 mN时的测头位移Fig.15 The displacement of the probe when P=2.98 N and z-directional probe force is 0.1 mN

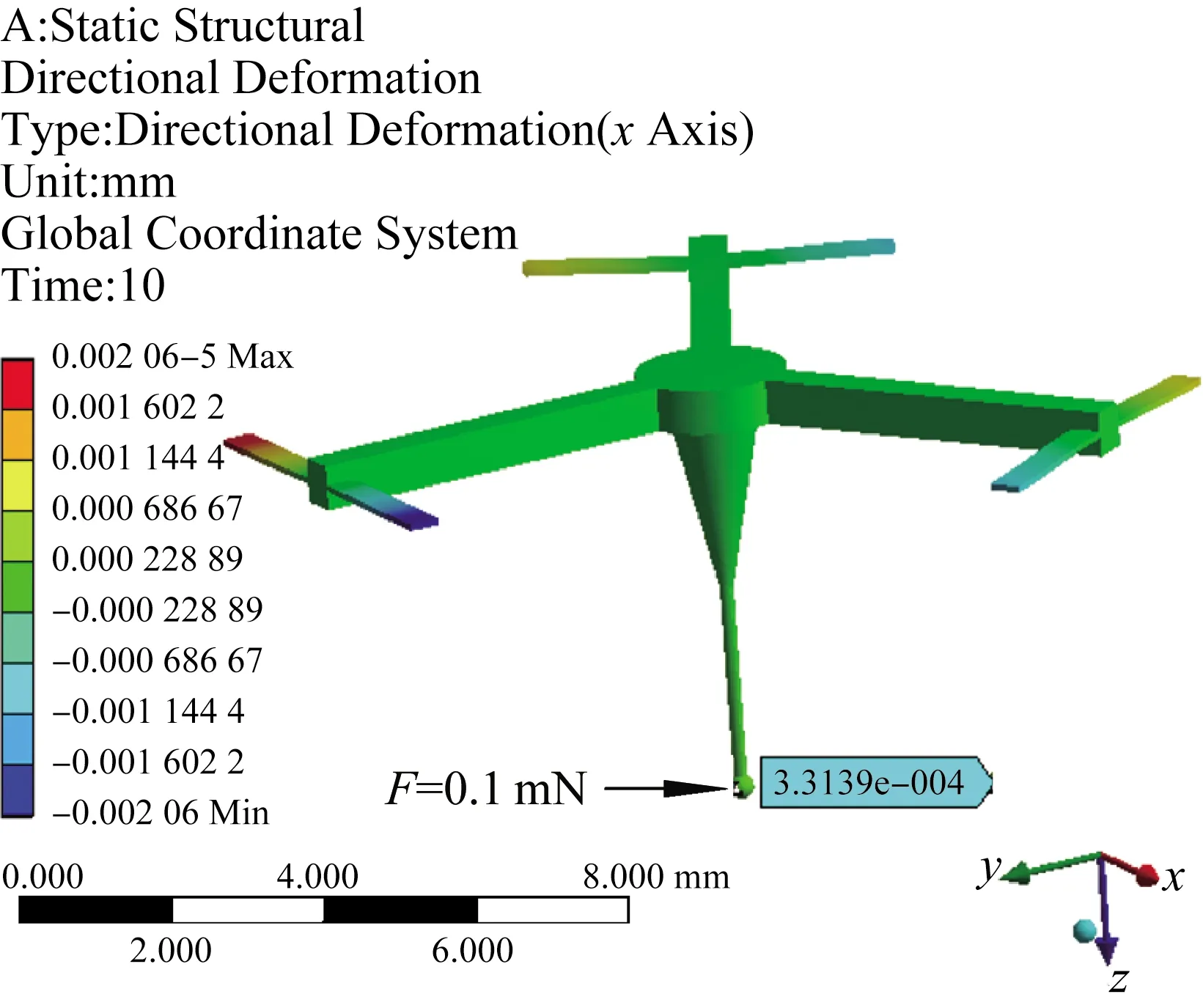
图16 当P=2.98 N和横向力为0.1 mN时的测头位移Fig.16 The displacement of the probe when P=2.98 N and lateral probe force is 0.1 mN

由图15和16可知，当施加P=2.98 N的压电驱动力时，对比测头约束支撑机构的初始刚度可知，测头具有显著的变刚度效果，且测头约束支撑机构具有各向同性刚度，测头的垂直刚度为0.299 9 mN/μm，测头的横向刚度为0.301 8 mN/μm。根据式(7)和(38)，当施加P=3.05 N的压电驱动力时，测头约束支撑机构的理论各向同性刚度值为0.294 9 mN/μm。由此表明，测头理论刚度和仿真结果较为符合，构建的测头刚度模型是正确的，为该类型的变刚度控制奠定了前期理论基础。

4 结 论

(1) 利用梁轴向受载以改变约束梁支撑刚度这一基本原理，构造了一种新型对称结构的三角梁变刚度约束微纳测头。

(2) 构建测头中心体力矩平衡方程，基于最小势能原理得到测头约束支撑机构的理论刚度模型，基于该模型进一步得到了微纳测头具有各向同性刚度时所需的压电驱动力大小。

(3) 给定约束支撑机构的尺寸参数，应用有限元仿真试验验证了理论刚度模型的正确性，得到了约束梁发生失效时的临界屈曲载荷，对研制出该类型测头的样机并开展变刚度控制试验研究奠定了坚实的理论基础。