基于BiLSTM-Attention模型的缺血性脑卒中的年卒中风险预测

骆轶姝， 邵圆圆， 陈德华

(东华大学 计算机科学与技术学院，上海 201620)

随着人工智能和大数据技术的发展，医疗模式逐渐从以治疗为主转变为以预测为主。脑卒中又称“中风”，是一种急性脑血管疾病，具有发病率、致残率、死亡率和复发率高的特点。未来5年里，相比心脏病、糖尿病等慢性疾病，脑卒中疾病在我国将以较快速度持续增长[1]。文献[2]研究表明，约94%的脑卒中发病因素都是可控的，根据患者当前生理状态及早对患病风险做出预判并加以预防，将极大地降低患者脑卒中发病率。

近年来，深度学习在缺血性脑卒中疾病预测研究中受到广泛关注。Hochreiter等[3]提出LSTM(long short-term memory)模型，增加长期依赖时序特征输入的学习模型，Graves等[4]在此基础上综合后向特征计算，提出BiLSTM(bi-directional long short-term memory)模型。基于这类深度学习模型的建立，姚春晓[5]构建了具有时序性的多层LSTM作为脑血管疾病预测模型。Chantamit等[6]参考国际疾病分类标准，构建LSTM循环神经网络模型对中风进行分类预测，将LSTM作为隐藏单元对数据特征信息进行挖掘，并利用自循环输出结果实现中风的分类预测。安莹等[7]提出心血管风险预测模型(risk prediction model for cardiovascular, RPMC)，综合考虑多种临床数据的融合学习，实现BiLSTM对电子病历数据的挖掘。Ma等[8]借助Attention机制增加模型的可解释性，实现利用电子病历数据对患者未来健康的预测。

上述研究为心脑血管疾病预测问题提供解决方法，但脑卒中疾病中急性缺血性脑卒占70%左右[9]，发病机制不同，选取疾病预判检查指标存在差异。因此，针对缺血性脑卒中的年卒中风险问题，将疾病辅助预测视为特征分类问题，建立深度学习预测模型。定义卒中发生和复发关键的一年，即12个月为时间周期。本文对来自某医院真实病历指标做缺血性脑卒中疾病影响多因子分析，在此基础上将患者当前检查以及基于回归预测思想构建的12个月后指标变化的时序数据作为输入变量，采用one-hot、归一化等数据预处理手段，将其转化为BiLSTM模型输入数据，以融合前向和后向的指标数据特征，并引入Attention机制，计算每个时刻特征与整个目标特征相似性以获得新的特征表示，最终以诊断标签作为输出变量，计算模型中的损失并采用优化算法对模型反向训练优化以获得较好的预测模型。

1 模型建立

1.1 问题描述

缺血性脑卒中的年卒中风险预测问题可描述为当前及未来t时刻预测指标数据X={x1，x2， …，xn}及对应标签Y={y1，y2， …，yn}，其中n表示样本患者数量，通过构建模型，由训练得到指标数据X与对应标签Y之间特征映射的预测模型。目标是当出现新的、未带有标签的患者指标数据时，模型能给出最优的年卒中风险预测结果Y′={y′1,y′2, …,y′n}。

1.2 模型结构

根据第1.1节中缺血性脑卒中问题描述，提出一种BiLSTM-Attention模型解决缺血性脑卒中的年卒中疾病预测问题。BiLSTM-Attention模型结构如图1所示。

图1 BiLSTM-Attention模型结构Fig.1 BiLSTM-Attention model structure

由图1可知，连接患者当前检查指标与预测未来12个月后变化指标形成输入样本，经BiLSTM隐藏层中神经元对特征进行计算，输出特征向量并传入Attention层，由该层判断输入时刻的特征对全局特征的重要程度，Dropout层通过设置丢弃率减少神经元个数，以防止模型出现过拟合，最后全连接层通过激活函数softmax进行连接。将上层特征映射输出为类别的概率作为对患病风险的结果预测。

1.3 BiLSTM原理

BiLSTM是基于LSTM模型结构改进而来的。LSTM模型是由结构相同的多个隐藏单元连接构成，一个隐藏单元由遗忘门、输入门、记忆细胞和输出门组成。LSTM隐藏单元结构如图2所示。

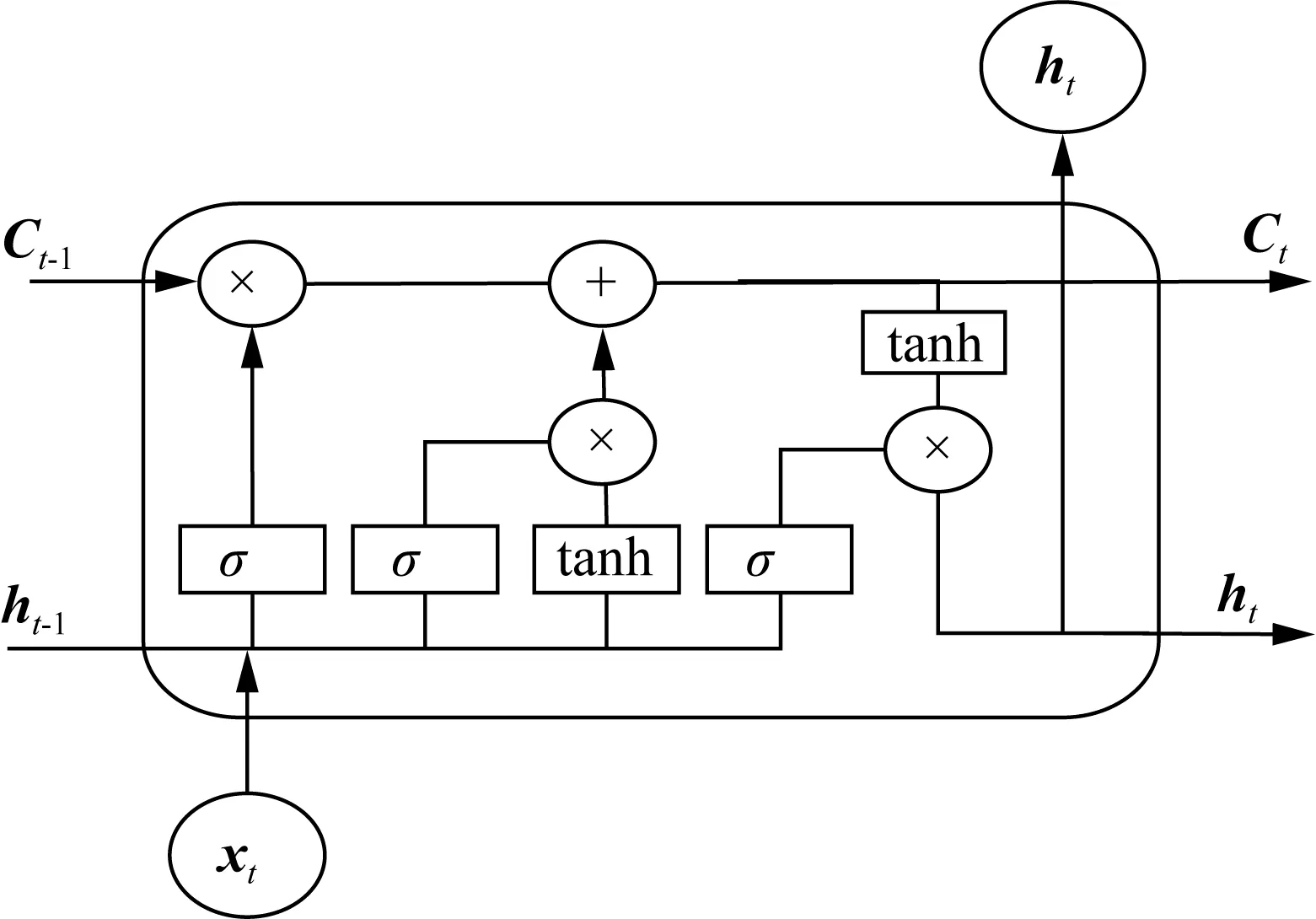
图2 LSTM隐藏单元结构Fig.2 LSTM hidden unit structure

由图2可知，t-1时刻隐藏向量ht-1和记忆细胞Ct-1及t时刻输入的特征向量xt，通过权值和激活函数的计算获取有效信息，并输出t时刻隐藏向量ht和记忆细胞ht，具体计算如式(1)～(6)所示。

ft=σ(Wf[ht-1，xt]+bf)

(1)

it=σ(Wi[ht-1，xt]+bi)

(2)

(3)

(4)

ot=σ(Wo[ht-1，xt]+bo)

(5)

ht=ot×tanh(Ct)

(6)

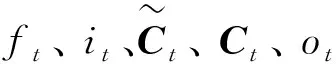
BiLSTM在LSTM模型基础上增加模型计算的复杂度，将LSTM的单向计算改为前向和后向的计算，并将两个方向的计算结果进行连接，以实现特征信息的双向学习。BiLSTM总体实现流程如图3所示。

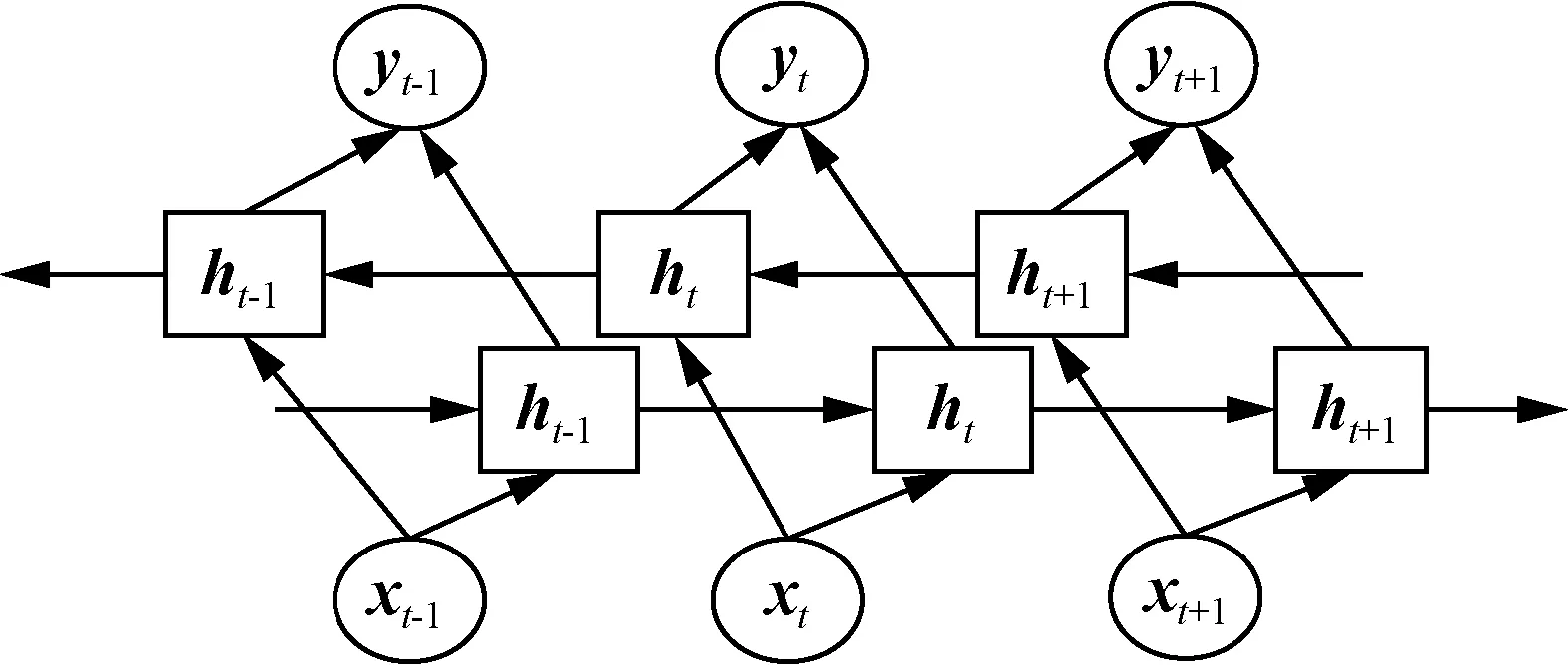
图3 BiLSTM总体实现流程Fig.3 Overall implementation process of BiLSTM

由图3可知，BiLSTM以LSTM作为隐藏单元，输入特征进入两个不同方向的模型结构中，通过隐藏单元特征计算，最后由该时刻的两个隐藏单元的输出向量连接构成该时刻输出，其中,yt-1、yt、yt+1分别为对应的t-1、t、t+1时刻的输出向量。t时刻BiLSTM计算如式(7)～(9)所示。

h(t-1)t=LSTM(h(t-2)(t-1)，xt)

(7)

h(t+1)t=LSTM(h(t+1)(t+2)，xt)

(8)

ht=[h(t-1)t，h(t+1)t]

(9)

BiLSTM模型的计算使每个时刻的隐藏层中信息将得到有效扩充的学习，有利于模型最终分类结果提升。

1.4 Attention机制

针对模型中可能存在忽略对关键特征信息的有效利用，增加Attention机制对时序特征信息的学习。该机制通过上层t时刻输出向量ht作为输入，计算特征权重αt，其计算如式(10)～(12)所示。

ut=tanh(Waht+b)

(10)

式中：Wa为权重系数；b为偏置系数。

(11)

式中：uw为初始化权重矩阵。

(12)

通过计算t时刻的输出对结果的重要性ut，计算ht的特征权重αt并输出向量Ct，对t时刻输入指标向量进行加权。计算得到的权重αt越大，表示该时刻隐藏层特征的重要程度越大，则该时刻的向量Ct对预测结果的贡献程度就越大。

通过上述计算，模型最终由全连接层中的softmax激活函数转化为二分类问题，输出年卒中风险发生概率y′i，计算如式(13)所示。

y′i=softmax(WiCt+bi)

(13)

2 缺血性脑卒中的年卒中风险预测

2.1 多因子确定

为筛选与缺血性脑卒中疾病发生的影响指标，采用Logistic逻辑回归分析法确定影响疾病的多重因子，该分析方法被广泛应用于医学疾病影响因子分析研究中自变量与因变量之间的因果关系。该依赖关系通过回归系数表示，计算类别概率，再得出回归系数，计算方法如式(14)和(15)所示。

(14)

(15)

式中：j为因变量；x为自变量；k为自变量的个数。

当k=1时，模型进行单因素分析，建立单一自变量对因变量的影响程度分析；当k>1时，模型进行多因素分析，建立的多个自变量同时变化，对因变量结果产生影响。综合两种分析以寻找疾病发生发展的多危险因子。

2.2 输入输出变量的确定

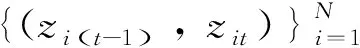
(1) 输入变量输入数据X。通过确定的z计算融合卷积神经网络(CNN)的LSTM非线性回归预测模型，根据当前t-1时刻指标zt-1拟合未来t时刻zt中连续型数值的变化z′t，如式(16)所示。

z′it=σ(LSTM-CNN(zi(t-1)，zit))

(16)

t-1和t时刻的数据组成的时序输入变量X， 如式(17)所示。

X=concat(zi(t-1)，z′it)

(17)

(2) 输出变量风险预测结果Y′。获取L标签，转化为一维数组，得到患者t时刻的真实标签Y，如式(18)所示。

Y=[y1，y2， …，yn]

(18)

式中：yi∈li,i=1，2，…，n。

根据X和标注真实标签Y的转化，最终由模型寻找X与Y之间的特征关系，风险预测结果Y′如式(19)所示。

Y′=softmax(BiLSTM-Attention(X，Y))

(19)

2.3 数据预处理

采用one-hot作为一种通过N位状态寄存器对N个状态编码实现离散特征映射到欧氏空间的独热编码方式。在分类问题中，一方面提高模型的计算特征之间距离的效率，另一方面对数据特征的维度有了一定的扩充作用。同时，为减小数据在不同维度影响的训练效果，采取归一化的处理，如式(20)所示。

(20)

式中：Imin和Imax分别为指标I数据中的最小值和最大值。

通过计算指标中最大值与最小值的差值比，将指标数据压缩到同一范围。

2.4 模型训练

模型训练中每一步都经损失函数计算误差，并使用优化器反向调整更新，以寻找模型效果最优的参数设置。

计算损失：交叉熵损失函数被广泛应用于二分类损失问题，通过计算预测值与真实标签之间的误差，反映模型训练效果。交叉熵损失函数如式(21)扭洋。

(21)

式中：n为样本数量。

通过极大似然运算，计算年卒中风发生概率y′i与真实标签yi的损失差异。

优化器：为减小模型训练损失且不产生局部最优结果，选取Adam优化器进行反向计算以调整网络权重参数。将计算梯度的一阶矩估计和二阶矩估计作为不同的参数设计自适应性学习率。

根据目标损失函数f计算出t时刻的梯度gradt，如式(22)所示。

gradt←Δθft(θt-1)

(22)

计算梯度gradt一阶、二阶矩估计值mt、vt，如式(23)和(24)所示。

mt←β1mt-1+(1-β1)gradt

(23)

vt←β2vt-1+(1-β2)gradt2

(24)

式中：β1、β2为矩估计衰减指数，分别默认为0.900、 0.999；θ为通过矩估计校正的更新参数。

缺血性脑卒中的年卒中风险预测模型训练算法如下：

Initializeθ0

ForiinT:

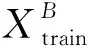
A←Attention(V)

Llogits←Matmul(A，θi)

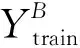
θi←Adam(Llearning_rate，Lloss)

End For

Evaluate(Xtest，Ytest，θ)

End

其中：T为训练步长；B为批大小数据集；Llearning_rate为学习率；Xtrain/Ytrain、Xtest/Ytest分别为训练集和测试集；V、A为特征提取层输出向量、注意力层输出向量；Lloss为模型训练误差；θi为第i次训练网络模型参数。

3 试验结果分析

3.1 试验数据

试验数据来源于上海市某医院的真实样本数据，共983名患者，其中，非缺血性脑卒中作为负样本共732名，缺血性脑卒中为试验正样本共251名。病历数据的选取充分考虑缺血性脑卒中疾病的发病机制，其中多因子筛选包含性别、年龄、高血压史、C反应蛋白(c-reactive protein， CRP)、总胆固醇(cholesterol， CHOL)、脱脂转化酶、斑块、狭窄程度以及内中膜厚度共计9个检查指标以及诊断结果标签，经输入变量处理后，均包含两次时间窗口为12个月左右的非稀疏数据。模型训练中，对该数据划分为80%训练集和20%测试集。

3.2 数据归一化处理

试验中，对所有输入样本数值均通过归一化处理方式压缩到[0， 1]。以选取1 000条CHOL浓度样本数据在归一化处理前后的特征比较为例。样本CHOL浓度归一化处理前后的结果如图4所示。

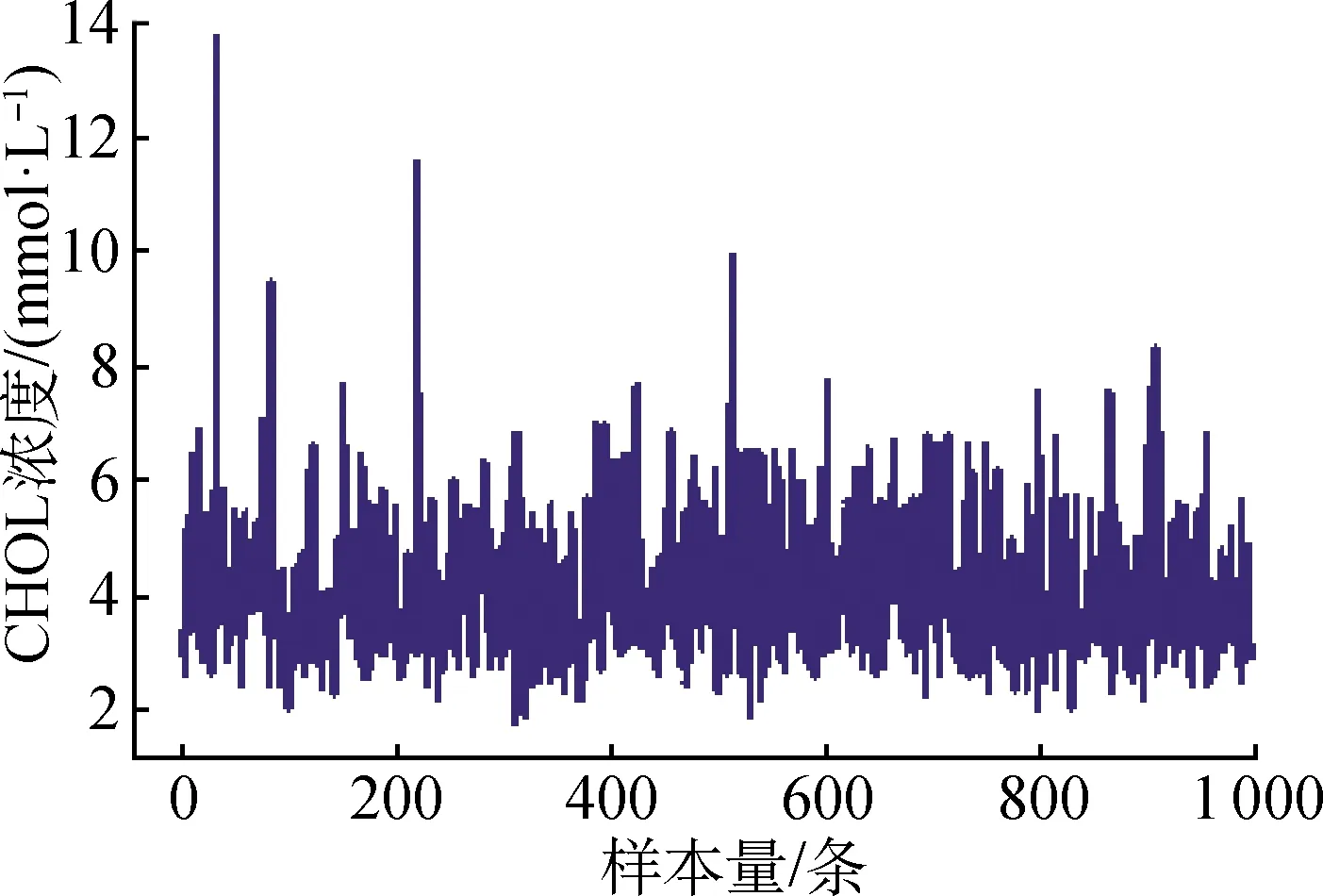
(a) 处理前

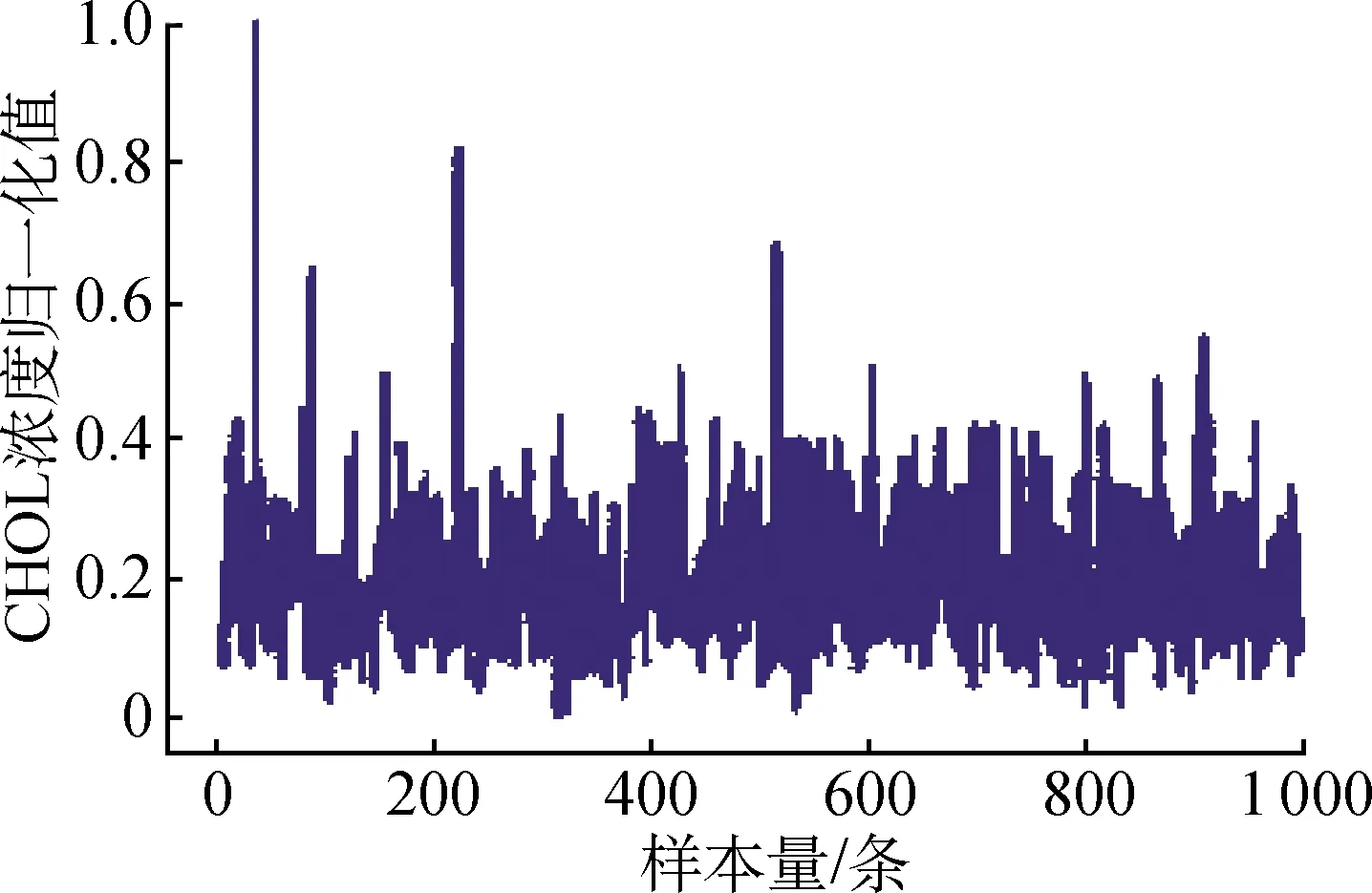
(b) 处理后

由图4可知，经数据转换，CHOL由[0， 14]被压缩到[0， 1]，并且保持原始数据的特征。

3.3 模型训练过程

试验中将加载预处理后当前检查数据与回归预测数据作为模型的数据集输入，具体模型训练过程如下：

(1) 输入2×9×1313大小的训练集样本，经预处理转化为(None， 2， 13)形状数据，即步长为2，维度为13，批大小随机的数据输入。

(2) 随机初始化网络参数，设置dropout=0.9， learning_rate=0.100， training_step=500。

(3) 训练数据经过双向LSTM学习后输出(None， 2， 32)的特征向量，经连接由注意力层对时序状态的加权，输出(None， 2)的上下文向量，最终softmax输出对缺血性脑卒中疾病是否发生的概率值。

(4) 将输出的预测值与真实标签计算交叉熵损失，网络中权重参数通过Adam优化器按照设置学习速率计算误差损失梯度反向优化更新。

(5) 按照训练步数，不断重复模型训练(1)～(4)过程。

训练过程中，采用控制变量法，分别对参数dropout、 learning_rate、 training_steps进行设值，其中learning_rate按0.100、 0.010、 0.001递减形式、dropout按步长为0.1改变、training_step按500步长的原则进行模型训练效果的比较。最终确定learning_rate=0.001， dropout=0.5， training_step=2 000时，模型训练准确度达最优。

3.4 结果分析

采用准确度(AAccuracy)、灵敏度(SSensitivity)、特异度(SSpecificity)、阳性预测率(PPPV)、阴性预测率(NNPV)及F1_score值评估标准FF1_score，衡量模型对缺血性脑卒中疾病诊断能力，计算方法如式(25)～(30)所示。

(25)

(26)

(27)

(28)

(29)

(30)

式中：TTP表示真实为缺血性脑卒中患者且被正确预测为缺血性脑卒中患者的数量；TFP表示真实为非缺血性脑卒中患者但被错误预测为缺血性脑卒中患者的数量；TFN表示真实为缺血性脑卒中患者但被错误预测为非缺血性脑卒中患者的数量；TTN表示真实为非缺血性脑卒中患者但被正确预测为缺血性脑卒中患者的数量。为获得年卒中风险最优预测效果，在不同条件下进行试验结果对比。受数据正负样本不平衡问题影响，试验采用SMOTE(synthetic minority oversampling technique)过采样进行正负样本的平衡。该方法一方面解决了样本不平衡所带来的分类预测性能差的问题，另一方面扩充了数据集中样本特征的多样性。SMOTE过采样前后试验结果如表1所示。

表1 SMOTE过采样前后试验结果Table 1 Experimental results before and after SMOTE oversampling %

由表1可知：SMOTE过采样后预测结果比SMOTE过采样前预测结果准确率高；受正负样本不平衡的影响，SMOTE过采样前，模型灵敏度较特异度结果低10%以上。这表示模型更多学习了负样本非缺血性脑卒中特征信息，因此对患者缺血性脑卒中患者确诊的遗漏情况较高；同理阳性预测率比阴性预测率低，这样模型在预测时会误判患者为缺血性脑卒中的诊断结果。当对数据采用SMOTE算法处理后，正负样本的试验结果明显提升且达到平衡的效果。

为测试不同模型训练拟合的效果，试验在LSTM、 LSTM-Attention、 BiLSTM以及BiLSTM-Attention等4种模型下进行预测结果的对比，试验结果如表2所示。

表2 不同模型下的试验预测准确率对比Table 2 Comparison of experimental prediction accuracy under different models %

由表2可知，4个模型预测总体准确率均达80%以上，对正负样本预测性能总体保持平衡。从横向结果对比看，单独的BiLSTM模型比LSTM模型在时序特征数据集的学习能力表现稍降低。这说明该模型结构对于本试验数据集相对复杂，性能上有所降低，但在增加注意力机制后，预测的准确度明显提升。此外，这也表示各时序特征分配了相应注意力权重值，其中各模型灵敏度差异较小，对正确判定缺血性脑卒中的能力无明显差异，但在非缺血性脑卒中诊断中，无注意力机制的模型遗漏情况较明显。从纵向结果对比看，灵敏度对比特异度以及阳性预测率和阴性预测率而言，其存在较小的差异。这说明过采样中的正样本存在与负样本界限模糊的情况，使得模型对其学习存在差异。在召回率和准确度上，由于在本试验数据中融合了注意力机制的BiLSTM模型，因此结果较好，总体性能具有一定优势，有一定辅助意义。

4 结 语

根据缺血性脑卒中疾病发生发展及数据特征，提出BiLSTM-Attention模型对缺血性脑卒中的年卒中风险发生进行预测。通过当前样本性别、年龄、高血压史、CHOL、 LPA、 CRP以及超声斑块等指标对其未来时刻CHOL、 LPA、 CRP指标变化的预测，使指标连接当前检查指标形成带有时间序列病历数据，实现基于BiLSTM的缺血性脑卒中的年卒中风险预测。同时融合Attention机制对关键特征加权，采用SMOTE对数据平衡处理，提升模型预测准确性，因此，在智慧医疗缺血性脑卒中的年卒中发展预测等方面具有良好的应用价值。由于试验数据为某医院真实数据，存在数据清洗不干净、数据观察窗口较短等不足，结果存在一定误差，未来希望针对该方面准确性开展进一步研究。