同轴气流作用下压电式微滴喷射过程的数值模拟

刘作平， 周 健， 裴泽光， b， 白 涛， 陈广锋

(东华大学a.机械工程学院；b.纺织装备教育部工程研究中心，上海201620)

基于微滴喷射技术的喷墨印刷按照微滴形成的方式主要分为连续式与按需式[1]。其中压电驱动的按需式喷墨印刷技术利用压电材料的逆压电效应产生驱动力从而喷射出微滴，其由于具有响应速度快、效率高、可实现按需喷射等优点而被广泛应用[2]。压电式喷墨过程包含复杂的流体形态变化，因此通过数值模拟研究微滴的成形过程，有助于明晰微滴喷射的内在机制，这对基于压电式喷墨印刷系统的技术改进具有重要意义。

近年来，为满足喷墨印刷精度与速度的要求，微滴喷射技术不断向精密化和高速高效化发展。薛光怀等[3]设计并加工一种压电式微滴喷头，并在微滴喷射平台上进行微滴喷射试验，通过改变高电平时间和增加压电片的自由振荡衰减阻值可提高微滴喷射的最高频率；刘赵淼等[4]设计一种用于生成均匀微滴的压电驱动式微滴喷射装置，采用数值模拟和试验相结合的方法，研究不同控制参数下的膜片振幅及其对生成的微滴的尺寸和均匀性的影响；周健等[5]设计并制造一种利用同轴气流对微滴飞行过程进行驱动的同轴气流辅助式压电微滴喷头。目前国内外研究者对于同轴气流雾化[6-7]、气-液流动聚焦[8-9]以及熔喷[10]等液体射流在同轴气流作用下的形成与流动特性已做了较多的研究与报道，但是对液滴在压电膜片与同轴气流共同驱动下的形成规律研究得相对较少。本文利用多物理场计算软件COMSOL Multiphysics对同轴气流作用下压电式微滴喷射过程和流体流动规律进行二维数值模拟，以明晰同轴气流作用下微滴的形成与运动特征。

1 模型的建立

1.1 计算区域

COMSOL Multiphysics是一个专业的基于偏微分方程对多物理场模型进行建模和仿真的科学仿真软件，其通过有限元方法模拟求解在科研和工程中能用偏微分方程(partial differential equation， PDE)描述的各种问题[11-14]。图1为同轴气流辅助式压电微滴喷头的结构示意图。为降低模型求解的计算量，考虑到进液通道与进气通道建模的特殊性，将设有同轴气流喷射槽的压电喷头中的微滴喷射过程由一个三维立体问题简化为二维平面模型。模拟计算时不考虑支撑体底座与上盖以及密封圈等部件的影响，整个喷头计算区域如图2所示，其中储液腔锥角为120°。喷头关键结构参数如表1所示。

图1 设有同轴气流喷射槽的压电式微滴喷头结构示意图Fig.1 Schematic diagram of the airflow-assisted piezoelectric printhead

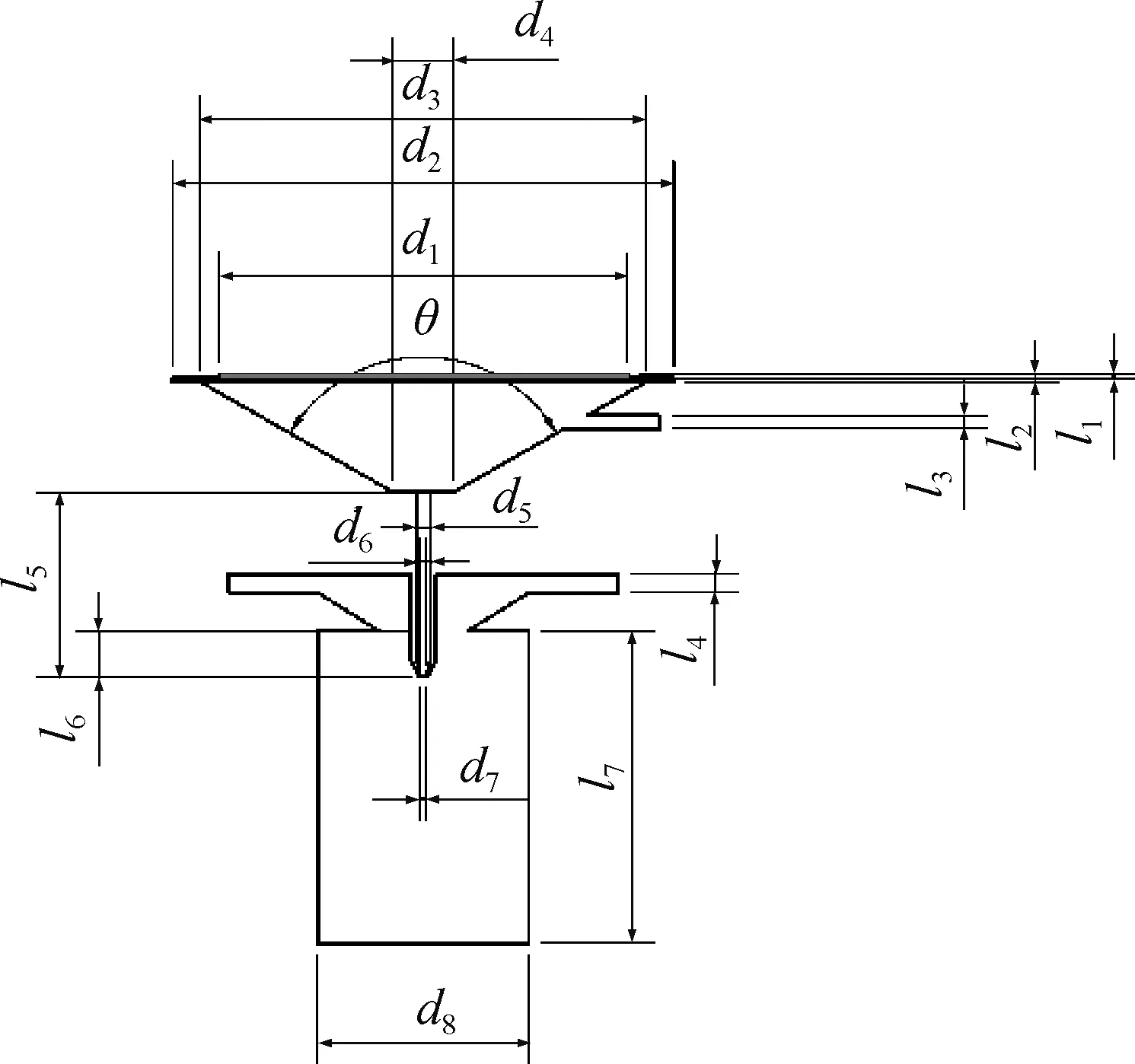
图2 喷头计算区域示意图Fig.2 Computational domain of the printhead

表1 喷头主要结构参数Table 1 Main structural parameters of the printhead mm

1.2 控制方程

模拟使用的液体为水(流体1)，密度为1 000 kg/m3，动力黏度为0.001 Pa·s，表面张力为72.75×10-3N/m，液体为不可压缩流；喷嘴外部区域及空气域中的流体为空气(流体2)，密度为1.225 kg/m3，动力黏度为1.789×10-5Pa·s。在设有同轴气流喷射槽的压电式喷头中压电致动器采用圆片薄膜式结构，由位于下方的薄铜片和上方的压电陶瓷片黏结而成。其中：薄铜片的密度为8 960 kg/m3，弹性模量为1.1×1011Pa，泊松比为0.35；所用的压电陶瓷材料为COMSOL材料库中的PZT-5H，与实际压电陶瓷材料相符，密度为7 500 kg/m3。其他主要参数包括刚度矩阵CE、介电常数矩阵λ以及压电耦合矩阵CB[15]，具体数值如式(1)～(3)所示。

(1)

(2)

(3)

压电材料的压电方程为

(4)

式中：S1、T1分别为水平方向的应变和应力；E3、D3分别为竖直方向的电场和电应力；λ为外应力为0或定值时的介电矩阵；d31为压电常数；CE为电场为0或恒定值时测得的压电陶瓷刚度矩阵。

采用层流两相流水平集的方法，将流体视为不可压缩流，采用Navier-Stokes方程[16]对喷腔体内与喷嘴内的流体进行模拟分析，如式(5)～(6)所示。

Fg+Fst+Fext+F

(5)

(6)

式中：p为压力；I为单位张量；Fg为喷腔体内流体的重力；Fst为两种流体界面的表面张力；Fext为外界自由能引起的体积力；F为作用在压电陶瓷片上的外力；ρ为密度，其是水平集方程的函数，如式(7)所示；μ为动力黏度，如式(8)所示。

ρ=ρ2+(ρ1-ρ2)φ

(7)

μ=μ2+(μ1-μ2)φ

(8)

式中：ρ1、ρ2分别为流体1与流体2的密度；μ1、μ2分别为流体1与流体2的动力黏度；φ为水平集函数；流体1对应于φ>0.5的区域，流体2对应于φ<0.5的区域。

两相流交界面的表面张力Fst=σkδn，其中，σ为表面张力系数，k为曲率，δ为集中于交界面的狄拉克函数，n为交界面单位向量。k取决于水平集函数φ的二次派生，这会引起表面张力精度的降低，因此根据变形公式(9)来计算Fst。

(9)

Fext在使用相场交界面时需要被计算到方程中，其表达式如式(10)所示。

(10)

式中：∂f/∂φ为外界自由能源。

1.3 数值模型、网格划分与边界条件

采用COMSOL有限元仿真软件建立设有同轴气流喷射槽的压电喷头的二维多物理场耦合模型，并添加两相流水平集、流固耦合与固体力学物理场。其中：空气域以及水域添加两相流水平集多物理场，并设置流体流动属性为层流。将薄铜片与喷腔体的接触面设置为流固耦合界面，耦合类型选择全耦合。固体域选择为压电陶瓷片与薄铜片，并将模型中的压电陶瓷片设置为静电物理场，用以模拟压电驱动过程，施加在压电片上的驱动电压波形如图3所示，电压波形参数如表2所示。此外，将压电陶瓷片下边界设置为接地属性以进行静电场仿真。

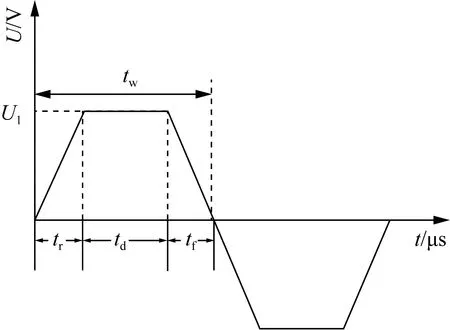
图3 驱动电压波形Fig.3 Waveform of driving voltage

表2 电压波形参数Table 2 Parameters of voltage waveform

带同轴气流的压电式微滴喷头网格划分图如图4所示。其中：压电陶瓷片与铜片的网格类型为自由剖分四边形网格，最大单元大小设置为0.05 mm；其他部分为自由三角形网格，设置网格大小为极细化。使用COMSOL软件中的mesh refine功能对模型的关键计算区域压电片及喷嘴部分进行局部网格加密，其他区域保持相对较大的网格密度。每组仿真计算时都需要多次调整网格的数量以确保求解精度，最终调整得到每组仿真的网格数量为30万～40万。喷腔体进液口初始条件为边界无压力并且设置为自动进液且抑制回流；进气口边界条件为作用于压电式喷头的同轴气流的法向速度值；两相流交界面为喷嘴与空气接触面；微滴喷射出口为外界环境边界，边界条件设置为无压力。将储液腔内壁、进液通道内壁面、喷嘴内外壁面与端面、进气通道内壁面设置为固壁，分析模型为瞬态分析，模型的仿真总时长为15 000 μs，仿真时间步长为250 μs。

图4 喷头网格划分情况Fig.4 Grid generation of the printhead

2 同轴气流作用下压电式喷头喷射过程的速度场与压力场

2.1 喷射过程的速度场

图5为同轴气流流速v=0 m/s时一个喷射周期内的速度分布图，其中位于喷头左侧的图例代表整个区域内流场的速度。从图5可以看出：当同轴气流流速为0 m/s时，由于液体重力的作用，喷腔体的液体均流向下方并进入喷嘴，此时喷嘴内液体的流速最大，但由于此时喷腔体内部还未充满进液，故喷嘴内液体的速度约为0 m/s。随着进液口液体速度的增大，喷嘴内的液体速度因压电片向上运动而减小，随后由于进液口不断进液以及压电片向下运动挤压喷腔体内的液体，进液口与喷嘴内液体的速度持续增大，约为0.12 m/s，如图5(c)所示。由于没有引入同轴气流，喷嘴周围的气体速度变化极其微小。当t=4 500 μs时，位于喷嘴正下方的空气域向左右两侧扩散最终形成两个非常小的涡旋，此时进液口速度最大，约为0.23 m/s，如图5(d)所示。

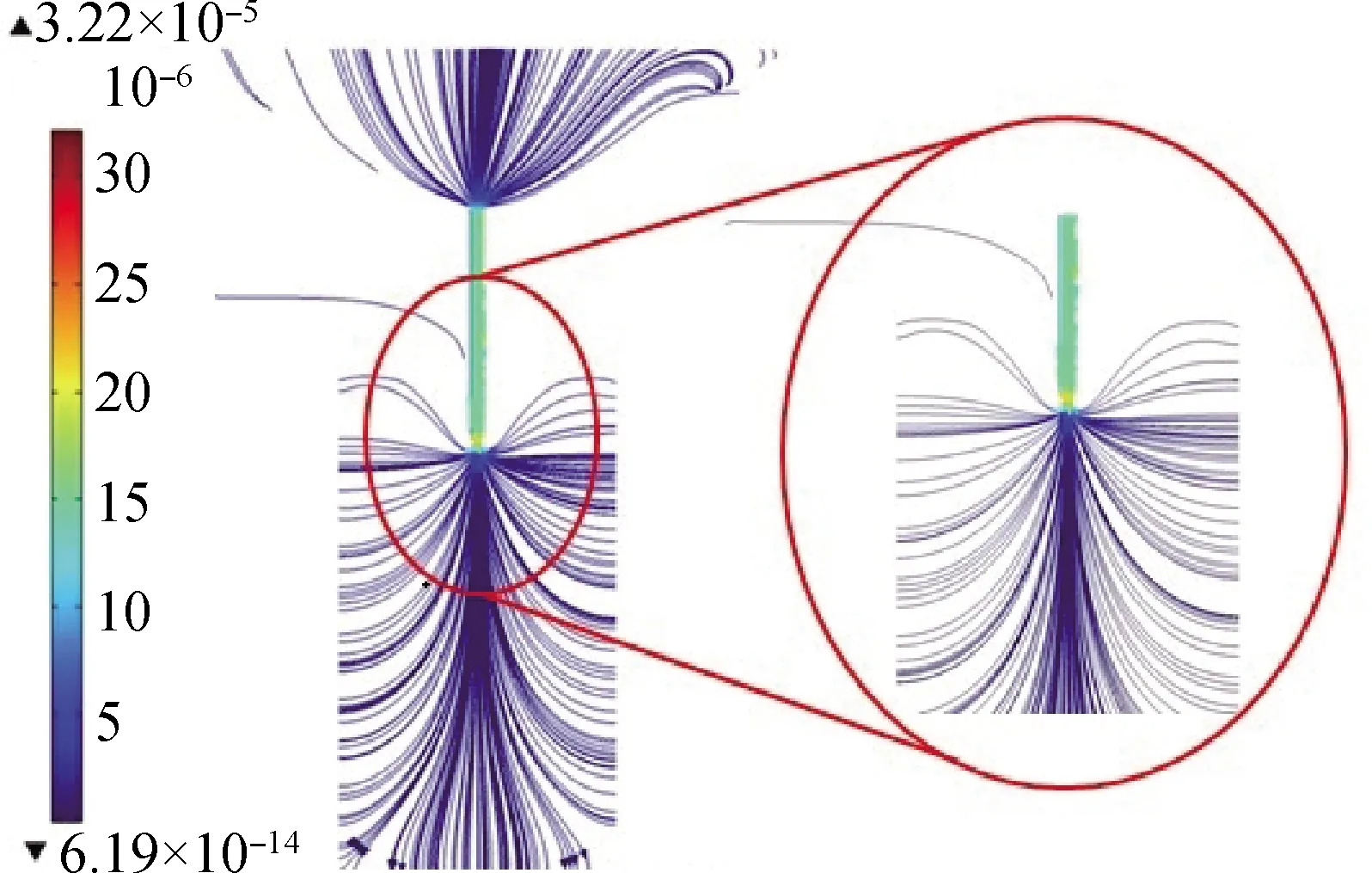
(a) t=0 μs

(b) t=1 500 μs

(c) t=3 000 μs

(d) t=4 500 μs

同轴气流流速v=10 m/s时一个喷射周期内的流场速度分布如图6所示。从图6可以看出：t=0 μs时，进气口开始流入气体，从进气口流入的气体首先填充至进气口以及气流喷射槽，进气口处的气流流速约为0 m/s，此时从进气口流入的气体对喷嘴下方空气流动的影响可以忽略，随着气流不断地从进气口流入，气体涡流区开始形成，在空气域内喷嘴出口两侧形成一对涡旋[17]，此时进气口处气流流速约为13.5 m/s。随着进气口气流流速的不断增大以及从气流喷射槽喷出的气体体积不断增大，涡流区的尺寸逐渐增大并且向喷嘴下游移动，t=3 000 μs时进气口气流流速约为15.1 m/s，空气域内形成两对涡旋，分别位于喷嘴出口两侧以及喷嘴出口正下方两侧。空气域内充分进气后，气体流速趋于稳定，此时进气口气流流速约为14.1 m/s，这时空气域内形成三对涡旋且逐渐增强扩大并继续向喷嘴下游移动，如图6(d)所示。

(b) t=1 500 μs

(c) t=3 000 μs

(d) t=4 500 μs

2.2 喷射过程的压力场

喷头内部液体压力场的变化对微滴形成过程具有重要的影响。图7为同轴气流流速v=0时一个喷射周期内的流场压强分布，其中，左侧图例表示除压电陶瓷片外其他区域相对于标准大气压的压强，右侧图例表示压电陶瓷片的运动位移(单位：m)，下同。

(a) t=0 μs

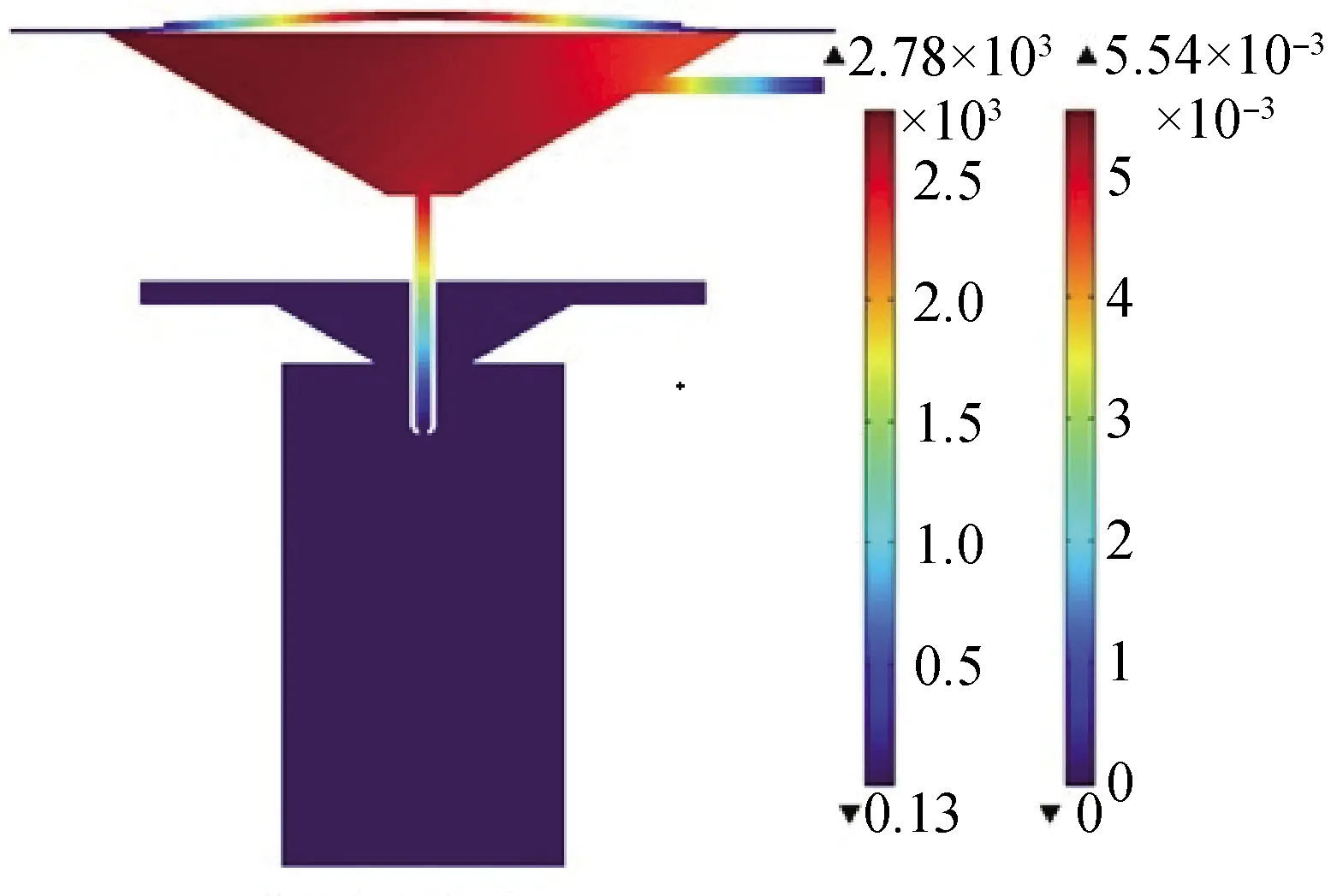
(b) t=1 500 μs

(c) t=3 000 μs

(d) t=4 500 μs

由图7(a)可以看出：受喷射液体自身重力的作用，储液腔内液体与硅胶管交界处B的压强大于储液腔内液体与压电陶瓷片交界处A以及玻璃喷嘴内液体与空气域交界处C的压强，此时最大压强为61.1 Pa； 压电陶瓷片受自身重力作用时，压电片位移约为0 μm。由图7(b)可以看出：当压电片受压电信号驱动而向上弯曲时，喷腔体内液体压强增大而喷嘴内液体压强保持不变，此时压电片中心点位移即压电片振幅为5.54 μm。 当压电片反向弯曲向下运动时，喷腔体内液体压强减小，玻璃喷嘴内部自进口端至出口端液体压强不断增大，并在液体与空气域交界的出口端面达到最大压强，如图7(c)所示。当压电片自下方最大位移处向上运动时，液体压强持续减小，如图7(d)所示。

同轴气流流速v=10 m/s时一个喷射周期内的流场压强分布如图8所示。

(a) t=0 μs

(b) t=1 500 μs

(c) t=3 000 μs

由图8(a)可以看出，受喷射液体自身重力的作用，储液腔内液体与硅胶管交界处压强最大，约为58.2 Pa，而压电陶瓷片受自身重力的影响，其位移约为0 μm。当压电片受到压电信号驱动向上弯曲时，喷腔体内液体压强增大而喷嘴内液体及空气域内气体的压强保持不变，压电片振幅为6.84 μm，与未施加同轴气流的情况相比，振幅有所增加，如图8(b)所示。当压电片受到压电信号驱动反向弯曲向下运动时，喷腔体内液体压强不断减小，玻璃喷嘴内液体与空气域交界面与进液口处压强达到最大值，喷头内的压强变化情况与未施加同轴气流时一致，空气域的压强因同轴气流的引入而显著减小，并且在喷嘴正下方两侧气流扩散而成的涡流区压力值减小更为显著，如图8(c)所示。当压电片受压电信号驱动逐渐恢复初始状态时，喷腔体内液体压强继续减小，喷嘴出口与空气域交界处以及进液入口处的压强处于较大值，空气域内压强较未施加同轴气流时大幅减小，两侧气流扩散而成的涡流区压强更低，如图8(d)所示。

3 同轴气流对微滴喷射行为的影响

3.1 同轴气流对微滴喷射过程的影响

图9为通过COMSOL数值仿真模拟得到的同轴气流流速分别为0和5 m/s时的微滴喷射过程。

由图9可知，微滴喷射过程可分为以下3个阶段：

(1) 微滴的喷射与延伸阶段。初始阶段由于压电片未发生变形，喷腔体内压强保持初始值，喷腔体内部的流体受表面张力和分子间作用力的影响而处于相对稳定状态。当t=1 500 μs时压电片反向弯曲并在喷嘴处形成内凹的弯月面。接着压电片受脉冲信号作用向下弯曲挤压喷腔体内的液体，压力波通过喷腔体中的液体传播至喷嘴处开始形成液面凸起(t= 2 000～2 500 μs)，随后凸起的液滴迅速向下延伸为前端近似半球形的液柱(t=3 000～4 000 μs)。

(2) 微滴断裂时刻。从图9(a)可以看出，未施加同轴气流时，液滴的断裂时间为t=4 500 μs。从图9(b)可以看出，当同轴气流流速v=5 m/s时，微滴断裂时间为t=5 000 μs。由此可知同轴气流的引入使微滴的断裂时刻延后，这与周健等[5]的试验结果是相吻合的。

(3) 微滴飞行阶段。微滴发生断裂后因小曲率半径而被剪断的尾部末端的压强较高，故尾部的液体向半球形头端流动，出现无约束长液带退缩现象，如图9(a)中t=4 500～6 500 μs与图9(b)中t=5 000～ 7 000 μs时的微滴喷射图所示。但由于微滴头部速度仍大于尾部，此时微滴形成的长液带发生断尾或多重碎裂，分裂后的微滴尾部逐渐由圆形收缩为小球状而成为卫星液滴。主液滴与卫星液滴分离后均失去了喷嘴内液体的推力作用并受到一定的空气阻力，进而喷射速度相比喷嘴中新喷射出来的液柱有所降低。于是从喷嘴挤压出来的第二股液柱开始融合第一个周期结束后形成的卫星液滴与主液滴，如图9(a)中t= 7 000～8 500 μs与图9(b)中t= 7 000～9 000 μs 时的微滴喷射图所示。融合后进一步分裂出主液滴与卫星液滴，如图9(a)中t=8 500～ 9 000 μs以及图9(b)中t=9 000～9 500 μs时的微滴喷射图所示。同轴气流流速v=0 m/s时新形成的主液滴由于液滴合并时其动能与表面能的相互转换将以椭球形向下方飞行，如图9(a)中t=9 000～10 500 μs时的微滴喷射图所示，而同轴气流流速v=5 m/s时新形成的主液滴则直径变大，形状更接近球形，如图9(b)中t= 9 500～10 500 μs时的微滴喷射图所示。

3.2 同轴气流对微滴延伸过程的影响

不同速度的同轴气流作用下微滴即将脱离喷嘴时的形态如图10所示。由图10可知，在表面张力作用下，液柱前端逐渐缩聚成半球形，成为微滴头部，此时液柱上存在两个曲率半径较小的位置，即A、 B处。其中，B处的曲率半径比A处小，且位于喷嘴出口附近，A处位于圆柱状液柱与微滴球状头部连接处。

(b) v=5 m/s

(c) v=10 m/s

(d) v=15 m/s

图11为同轴气流流速对微滴断裂前A处微滴直径D的影响及其随时间的变化情况。由图11可知，随着同轴气流流速的增大，A处液体增多，进而微滴直径变大。这是由于在液滴与气流交汇区域的左右两侧形成轴对称的若干股涡流，使得喷嘴正下方的压强减小，因此在同轴气流的作用下接近A处但位于其上游的表面液体沿液柱向下游加速流动，并且同轴气流的流速越快，A处液体增加越多。

图11 微滴断裂前直径随时间变化Fig.11 Variation of droplet diameter before fracture over time

在微滴形成过程中，微滴的总长度L被定义为微滴前端与喷嘴出口端面的垂直距离，其从微滴开始自喷嘴处凸起时逐渐增加，受到同轴气流作用时，A处上游的表面液体沿着液柱向下方加速流动使得整个圆柱状液柱段不断变长。微滴断裂前微滴的长度随时间的变化情况如图12所示。

图12 微滴断裂前长度随时间变化Fig.12 Variation of droplet length before fracture over time

由图12可知，随着同轴气流流速的增加，微滴长度变长且微滴断裂时刻延后。当v=15 m/s时，微滴长度随时间延长而增加最为明显；当v=5与10 m/s时，微滴长度在t=3 500 μs之前变化并不明显。这是由于较小的气流造成的负压对于微滴表面液体克服其内部黏性力从而加速向下流动的作用不明显，因此不会使微滴长度产生明显变化。

4 结 语

利用COMSOL Multiphysics仿真模拟软件，建立设有同轴气流喷射槽的压电式喷头的微滴喷射流场模型，并通过数值模拟研究同轴气流的引入对于压电式喷头在喷射过程中射流速度场与压强场以及微滴喷射过程的影响。主要得出以下结论：

(1) 同轴气流的引入使得空气域内形成轴对称的成对涡旋，随着气流不断从进气口进入，涡旋数量增多且不断加强扩大并向喷嘴下游移动。

(2) 压电片的形变以及射流压强场呈周期性变化，同轴气流的引入使得压电片振幅变大，空气域的压强变小，且位于喷嘴正下方两侧由同轴气流扩散形成的涡流区域的压强变化更明显。

(3) 随着同轴气流流速的增大，微滴断裂时刻延后，微滴形状由椭球形趋于球形，微滴延伸长度增加，微滴直径增大。