创造性使用教材问题情境的实践与体会

吴银芳

摘要：教材是我國学校教育的主要课程资源，但不是唯一的课程资源。教师要创造性地使用教材，丰富“问题情境”的生活化背景，做实“问题情境”的活动化过程，彰显“问题情境”特殊化的优势，替换合适的“问题情境”，从而激发学生的思维，确保学生有效参与，获得探究思路，保障教学活动更具实效。

关键词：问题情境  丰富  做实  彰显  替换

教材一直是我国学校教育的主要课程资源，但不是唯一的课程资源。新课程标准倡导在数学教学活动中教师要创造性地使用教材，积极开发和利用各种教学资源，为学生提供丰富多彩的学习素材。如何领会和把握教材，提高课堂教学效率？笔者就创造性使用人教版初中数学教材中“问题情境”这一角度来谈谈自己的教学实践与体会。

一、丰富“问题情境”的生活化背景，激发学生的思维

生活中处处有数学，教材所选择的素材大多来源自然、社会中的现象和问题，其中不乏与现实生活有关的图片等。但善于挖掘、钻研教材的教师一定会发现教材中的这一类问题情境有很大的开发空间。如“9.1.1不等式及其解集”引例：一辆匀速行驶的汽车在11：20距离A地50 km，要在12：00之前驶过A地，车速应满足什么条件？

直接由此情境引导学生分析不等关系、列出不等式，本无可厚非，但却忽视了知识间的逻辑关系。同时教材中“问题情境”的数学味过浓，也不利于激发学生的求知欲，久而久之，学生面对数学课堂时会望而却步。而不等式与等式（方程）都是反映现实生活中数量关系的模型，它们之间有很多相似之处，采用类比教学更能顺应学生思维发展。基于以上考虑，我做了如下的设计：

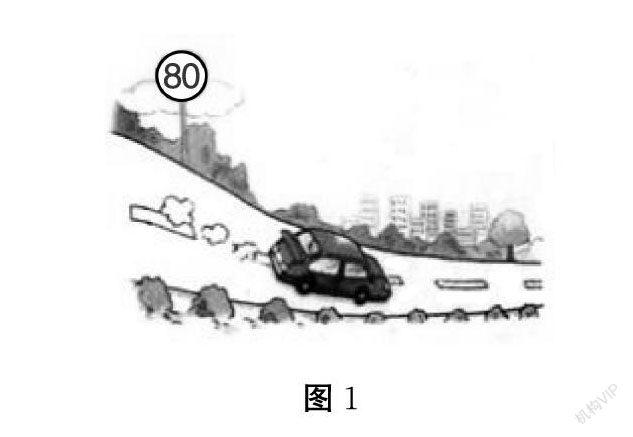
【初探新知】“五一小长假”，同学们喜欢与家人出门旅游和购物。5月1日小明一家自驾外出旅游，7：20距离景区还有50千米，汽车一直保持匀速行驶，若想在8：00准时到达景区，车速应满足什么条件？若想在8：00之前到达景区呢？

【再探新知】小明细心地观察后，开始担心能否在8：00之前到达景区，你有什么看法？

将情境改为“假期出游问题”，让学生置身其中。问题设计由学生熟悉的利用相等关系列方程，再到利用不等关系列不等式，为类比学习奠定基础。图2中增设限速标志，贴近生活实际，为【再探新知】环节中不等式的解及解集的引入埋下伏笔。

丰富“问题情境”的生活化背景，从知识间的逻辑关系出发，立足学生的生活实际，采用合理的教学方法，更利于激发学生思维。

二、做实“问题情境”的活动化过程，确保学生的有效参与

对于教材提供的以“活动形式”创设的问题情境，教师应着力引导，加强预设，让学生积极主动地参与，谨防浅尝辄止。如“6.3实数”问题：我们知道有理数包括整数和分数，请把下列分数写成小数形式，你有什么发现？

52，-35，274，119，911

仅凭上述几个例子，就想引导学生发现“任何分数都可以化成有限小数或无限循环小数”这一结论，还远远不够。这种情况下，总结的结论是教师灌输给学生的，对于学生而言，知识的获得是匆忙的、低效的，甚至是无效的，他们对于像“119，911”一样可以化为无限循环小数的分数认识还不够充分。考虑到学生的认知能力，我在学生发现“它们可化为有限小数或无限循环小数”之后，追问：

（1）是不是所有的分数都是这样的？谈谈你的想法。

（2）不妨举几个你认为既不能化为有限小数又不能化为无限循环小数的分数，我们来试一试。

学生列举分数，教师组织他们分组探究、验证想法。有了足够的例子作为依据，

学生逐渐认清了分数的本质。

牢固的基础知识、正确的逻辑推理都是后继学习的基础，而引导学生亲历新知建构的全过程，给予他们充足的时间和空间，暴露认知障碍、解决和跨越障碍，这种看似“费时”的教学才有实效。

三、彰显“问题情境”特殊化的优势，启发学生获得探究思路

数学学习是由学生主动参与的再创造、再发现的过程。教师要善于结合教材给出的问题情境，本着“发展性”的原则，由特殊到一般地启发学生获得探究思路。如“17.2勾股定理逆定理”，教材在介绍古埃及人画直角方法之后，设计了一个画一画的动手操作活动：如果三角形的三边长分别是2.5 cm，6 cm，6.5 cm，它们满足关系“2.52+62=6.52”，画出的是直角三角形吗？换成4 cm，7.5 cm，8.5 cm，再试一试。

这种操作、计算、归纳和猜想的过程是典型的几何探究过程，其价值局限于命题2的提出。由于勾股定理与勾股定理逆定理联系紧密，我做了如下的设计。

问题1：勾股定理揭示了由形的关系到边的数量关系。直角三角形的两条直角边长分别为3 cm和4 cm，斜边长为多少？

问题2：反过来，由边的数量关系能否得到形的关系？

教材中古埃及人围成的三角形的三边有何关系？以3 cm，4 cm，5 cm为三边真的能得到一个直角三角形吗？我们一起画画看。

问题3：对比你所画的三角形，它们有什么联系？除了度量的方法，你能用什么方法说明它是直角三角形吗？

学生经过练习，进行逆向思考和操作活动后，在教师的有意引导下获得探究活动的“副产品”——构造三角形全等的证明思路。这样的设计有效突破“用同一法证明勾股定理逆定理”的教学难点，对学生思维进行了全面的训练。

教师要善于分析学生认知的生长点，选择让学生动手实践的合适时机和内容，让学生在操作活动中获得直观感悟，同时教师还应引导学生做深层次的思考，促进学生思维发现，获得探究一般性问题的思路，达到事半功倍的效果。

四、替换合适的“问题情境”，保障教学活动更具实效

同知识与信息极度丰富的现状相比，教材内容相对稳定，因此在教学实践中，创设有利于自身教学实际的“问题情境”来替换教材中的“问题情境”非常必要。如“10.1统计调查”中：在新闻、体育、动画、娱乐、戏曲这五类电视节目中，你最喜欢哪一类？

据以往的教学实践结果反馈：学生最喜欢的节目中动画、娱乐所占比例较大，新闻、体育所占比例次之，戏曲类节目容易爆冷门。对于小班额的学生，甚至调查发现喜欢戏曲类节目的人数为零。这样的结果有违教材编写的初衷，给后面的描述数据也带来不便。慎重考虑后，将其替换成下列情境：

动画片《喜羊羊与灰太狼》深受学生喜爱。在懒羊羊、喜羊羊、美羊羊、沸羊羊、暖羊羊这五只小羊中，你最喜欢哪一个？

替换合适的“问题情境”，实际上有效地将教学内容的普遍性与学生学情的特殊性结合起来，这样做能充分调动教学双方的兴趣，使探究活动意图得以实现，提高教学实效。

数学教学理念以提高人的素养为本，“有效课堂”是我们永恒的追求。为此，我们应该根据教学目标的要求，遵循学生的实际情况和学习规律，在深入钻研教材的同时，创造性地用活、用实教材，培养学生可持续发展的数学能力，促使课堂教学更加灵动有效！

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]课程教材研究所中学数学课程教材研究开发中心.义务教育教科书数学教师用书（七、八年级下册）[M].北京：人民教育出版社，2013.