基于离散滑坡位移条件下油气管道受力分析*

李明

(济南大学；中国石油天然气管道工程有限公司)

0 引 言

我国地质条件复杂多样，尤其在西南各省山区和西北黄土高原地区，雨季来临时滑坡地质灾害较为常见。油气长输管道具有距离长、沿线分输点多和覆盖面广的特点，兼顾避绕人口密集区和城镇规划区的需求，在特殊情况下受场地条件限制时，不可避免穿越滑坡体，从而受到滑坡地质灾害的威胁。据统计，中缅油气管道在2014—2018年期间发生滑坡22起[1]，西气东输管道沿线统计滑坡155处，涩宁兰输气管道沿线统计滑坡13处[2-3]，因此长输油气管道受滑坡体影响的区段很多。当坡体稳定性遭到破坏而发生滑动时，管道在坡体滑动位移的作用下轻则会产生变形，重则会造成断裂、火灾和爆炸。为保障油气管道安全，需要对穿越滑坡区段油气管道的受力状况进行分析。

以往的研究成果中，陶勇寅等[4]将管道简化为弹性地基梁，考虑了管土之间的剪切应力，并给出了弹性地基梁的挠曲线微分方程，该方程可用于埋地管道弯矩、剪力和应力的计算；邓道明等[5]在滑坡地质灾害对管道破坏机理研究的基础上，进一步发展了滑坡作用下管道的内力和变形计算公式；刘慧[6]在前人分析的基础上，参考断层错动的相关研究，给出了管道在轴向滑坡、横向滑坡及圆弧滑坡作用下的解析方法；王联伟等[7]基于土弹簧模型对管道滑坡力学影响因素进行了分析，讨论了纵向滑坡和横向滑坡作用下管道受力情况。

目前大多数研究都是基于固定滑坡位移条件下的管道应力分析，考虑到滑坡体不同部位的滑动位移并不相同，采用固定滑坡位移对管道进行应力分析所得计算结果还不够精确，因此需要首先对滑坡体沿管道敷设方向各点的实际位移进行求解，然后再对管道相应位置施加离散滑坡位移，发现管道受力状况与滑坡体的滑动规律更为相符，并采用该方法分别对穿越纵向滑坡体管道和穿越横向滑坡体管道进行了受力分析。

1 模型建立

1.1 建立滑坡体模型

建立滑坡体模型用于求解沿管道敷设方向各点的滑动位移。滑坡体土壤本构关系选用Mohr-Coulomb模型，该模型假设坡体剪应力达到材料抗剪强度极限时即会发生破坏，可以用作模拟滑坡体土壤材料，其抗剪强度与其所受正应力呈线性关系[8]，表达式为：

τ=c+σtanφ

(1)

式中：τ为土壤材料的剪切强度，kPa；σ为切点的正应力，kPa；c为黏聚力，kPa；φ为内摩擦角，(°)。

采用有限元强度折减法模拟坡体的失稳滑动过程，将坡体所能提供的最大抗剪强度与外载荷在坡体内所产生的实际剪应力之比定义为强度折减系数，通过调整强度折减系数来降低岩土强度，直至坡体在外载荷作用下发生失稳滑动[9-11]。对于Mohr-Coulomb模型，强度折减系数可以表示为：

cm=c/Fr

(2)

φm=arctan(tanφ/Fr)

(3)

式中：cm为强度折减之后的黏聚力，kPa；φm为强度折减之后的内摩擦角，(°)；Fr为强度折减系数。

坡体是否发生失稳滑动的判定准则有3类[12-14]：①以有限元计算是否收敛作为判定准则；②以等效塑性应变自坡脚至坡顶是否发生贯通作为判定准则;③以坡面节点位移是否发生突变作为判定准则。其中坡体是否发生塑形贯通具有直观、易判断的特点，因此这里将其作为坡体是否发生失稳滑动的判定准则，然后提取沿管道敷设方向各点的滑动位移作为离散滑坡位移。建立滑坡体模型，坡顶长a，坡角α，滑坡体坡面长L，模型高h，坡体基础长b，滑坡体模型如图1所示。

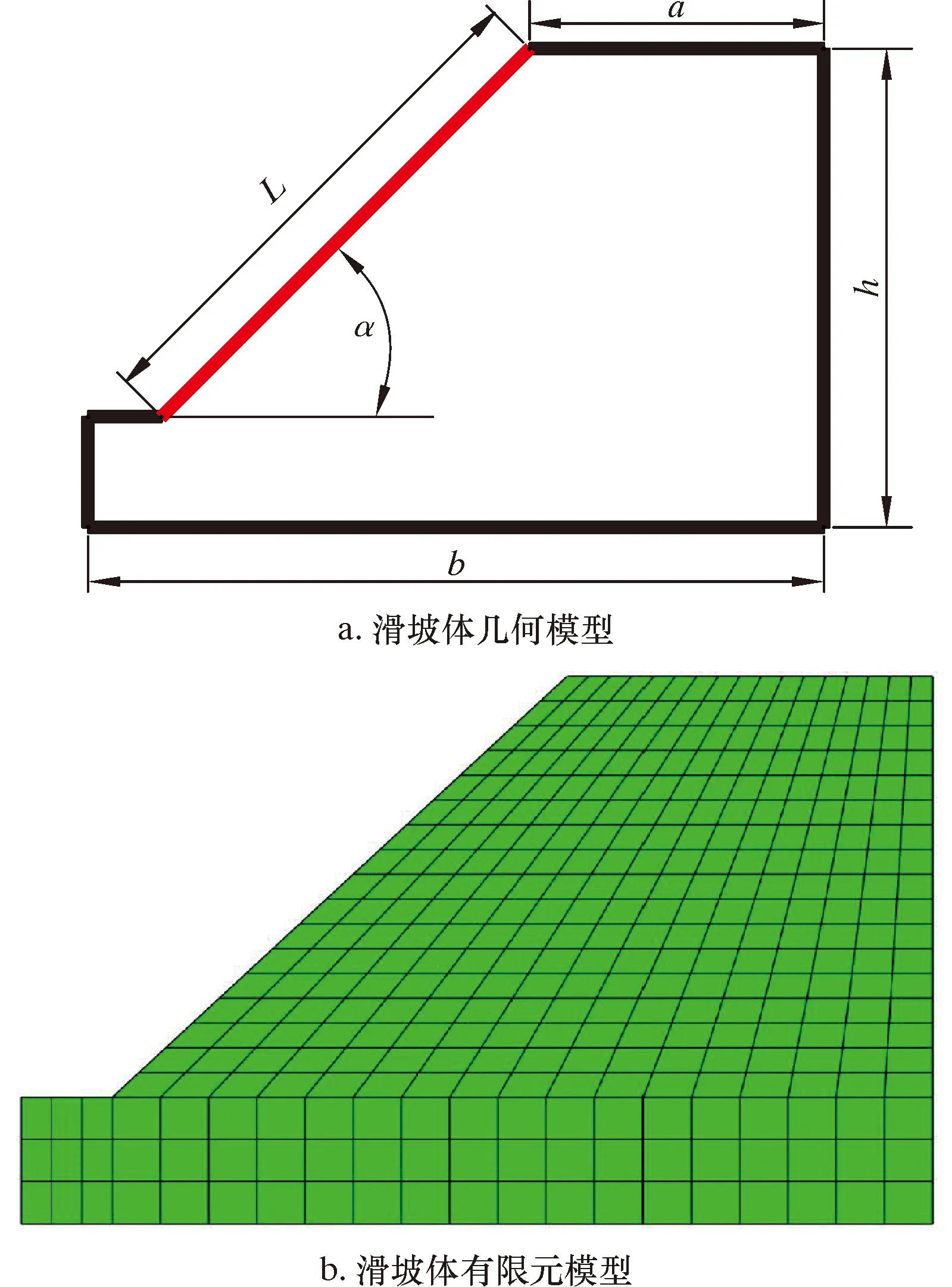
图1 滑坡体模型Fig.1 Sliding mass model

1.2 建立管土相互作用模型

建立管土相互作用模型用于求解离散滑坡位移条件下管道受力状况。管道材料具有非线性特点，其应力应变曲线可以根据GB/T 50470—2017中Ramberg-Osgood方程进行拟合[15]。管道本体采用PIPE20管单元模拟，该单元是具有拉压、弯曲和扭转性能的单轴单元，每个节点有6个自由度，即沿节点坐标系X、Y、Z方向的平动自由度和绕X、Y、Z轴的转动自由度，具有塑形、蠕变和膨胀功能[16]。土壤本体采用COMBIN39土弹簧单元模型。GB/T 50470—2017中列出了三轴土弹簧的计算公式，包含管道轴向、侧向、垂直向上和垂直向下土弹簧[17-21]。管土相互作用模型考虑了材料和几何大变形的非线性特征，可以实现离散滑坡位移条件下管道受力规律及失效因素分析[22-25]。

当管道纵向穿越滑坡体时，管道可分为坡底固定土体段、纵向穿越滑坡体段和坡顶固定土体段三部分，其中纵向穿越滑坡体段长度Lp与滑坡体模型中坡面长度L相等，这样滑坡体坡面各点滑动位移与相应位置管道所受位移载荷就可以一一对应，实现在管道上施加离散滑坡位移过程。当管道横向穿越滑坡体时，管道可分为左侧固定土体段、横向穿越滑坡体段和右侧固定土体段三部分，其中横向穿越滑坡体段长度为Wp，由于滑坡体上部、中部和下部位移分布并不相同，所以管道横向穿越滑坡体不同部位时需要分别进行受力分析。管道纵向和横向穿越滑坡体几何模型分别如图2和图3所示。

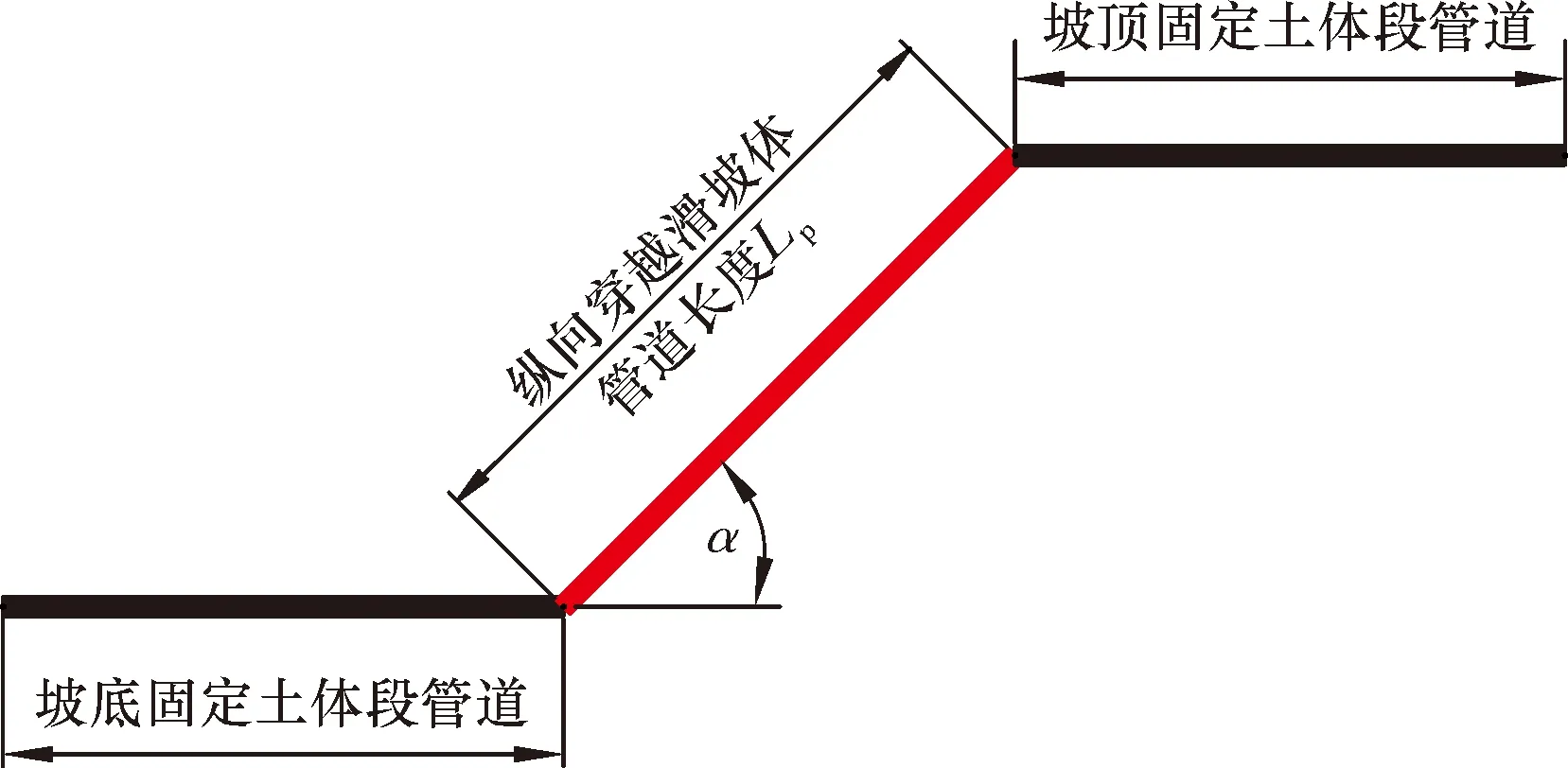
图2 埋地管道纵向穿越滑坡体几何模型Fig.2 Geometric model for buried pipeline to cross sliding mass vertically

图3 埋地管道横向穿越滑坡体几何模型Fig.3 Geometric model for buried pipeline to cross sliding mass horizontally

2 实例分析

2.1 基础数据

某一均匀土质滑坡体，L=100 m，α=45°，h=100 m，a=80 m，b=200 m，土壤容重γ=20 kN/m3，c=12.38 kPa，φ=20°，求解坡体滑动时坡面各点水平、竖向和总位移。某输气管道穿越该滑坡体，管道规格为D1219×27.5 mm，材质为X80，管道内压在0～10 MPa之间，管道运行时与下沟回填时的温差在0～50 ℃之间变化，管顶埋深1.2 m，当管道纵向穿越滑坡体时Lp=100 m，当管道横向穿越滑坡体时Wp=100 m，分别对管道纵向和横向穿越该滑坡体时进行受力分析。根据土壤参数计算土弹簧参数，结果如表1所示。

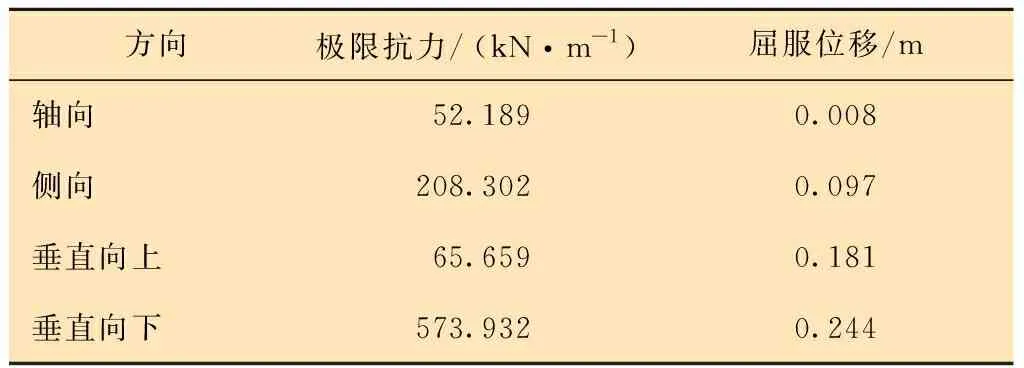
表1 三轴土弹簧参数Table 1 Parameters of triaxial soil spring

2.2 离散滑坡位移

当坡体发生滑动时，滑动面近似为圆弧形，自坡脚至坡顶沿管道敷设方向建立一条路径，该路径上土壤位移即为管周离散滑坡位移，其长度为100 m。根据有限元计算结果，沿该路径的竖向滑动位移绝对值逐渐增大，近似呈直线增长，说明滑坡体顶部主要发生竖向移动，而在滑坡体底部竖向位移较小；沿该路径的水平位移绝对值呈现先增长后降低的趋势，说明坡脚滑动面下部土体水平位移较小，而滑动面上部土体水平位移较大；滑坡体总位移呈现先增长后略有降低的趋势，说明滑动面上部土体总位移变化不大，位移最大点出现在坡脚滑动面附近。滑坡体位移分布如图4所示。滑坡体沿管道敷设方向位移的变化曲线如图5所示。

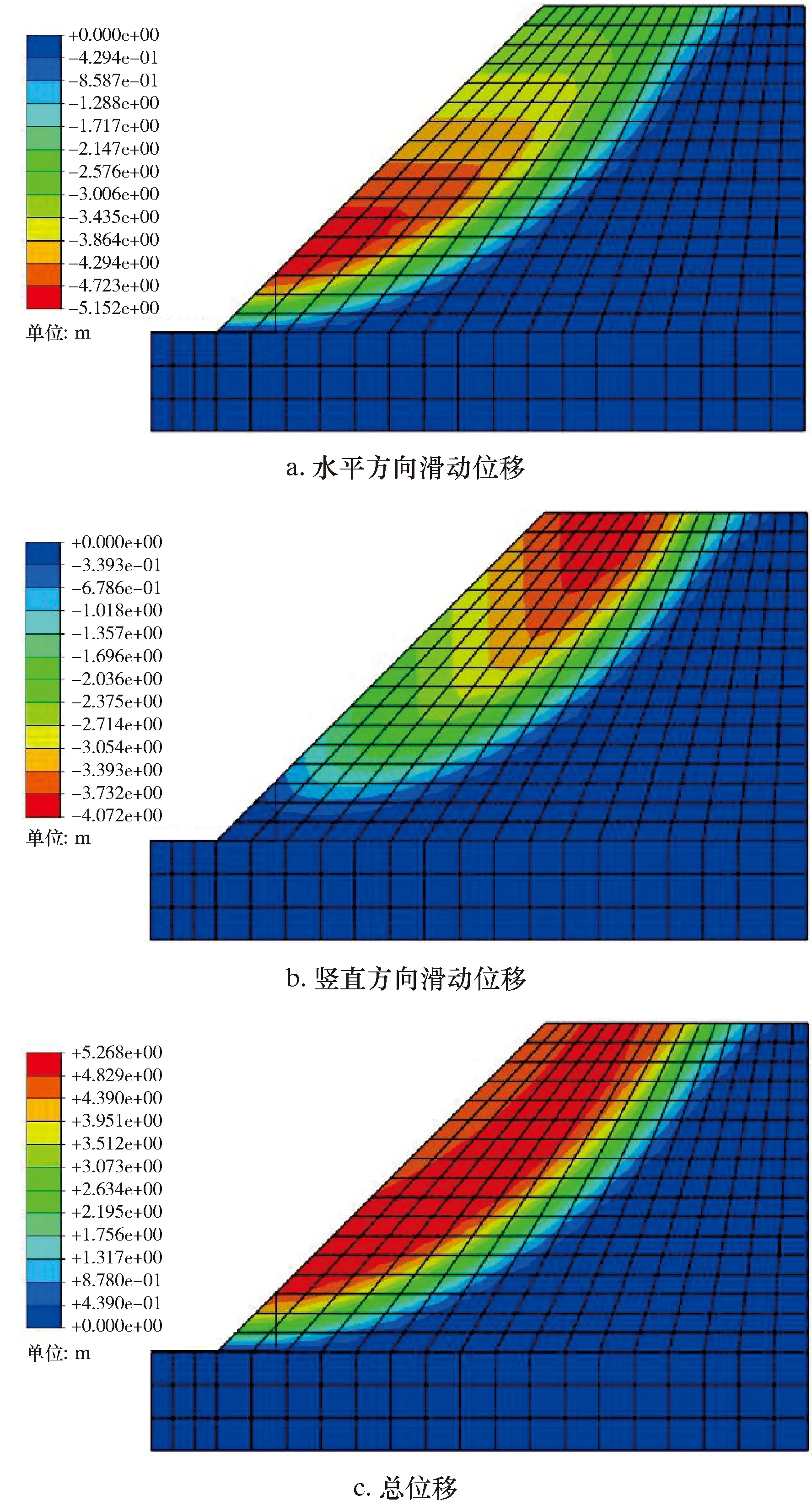
图4 滑坡位移分布云图Fig.4 Cloud chart for landslide displacement distribution

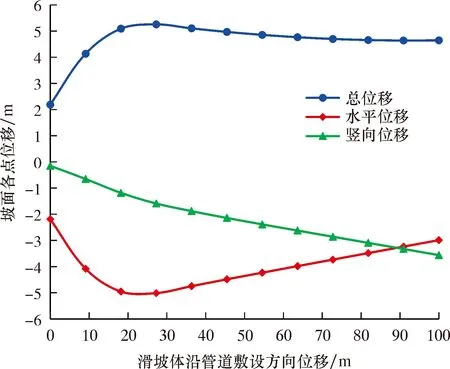
图5 滑坡体沿管道敷设方向位移的变化曲线Fig.5 Displacement variation curve of sliding mass in pipelining direction

2.3 纵向穿越滑坡体管道受力分析

当管道纵向穿越滑坡体时，将上述离散滑坡位移施加到对应位置的管道上，在管道几何模型中该区段管道长度为200～300 m。根据有限元计算结果，管道Mises应力极值点有4个，分别处于坡脚左侧水平段、坡脚弯管、滑动面附近和坡顶附近；管道最大Mises应力点在坡脚弯管处，主要由于该点不但承受了上部土体的滑动位移载荷，而且附近土体的滑动剪切作用还在该点产生了较大的弯矩；滑动面附近存在一处Mises应力极值点，主要由于土体的滑动剪切作用使管道产生了较强的应力和较大的弯曲变形；坡脚左侧水平段管道也有一处应力极值点，主要由于坡脚弯管在土壤载荷作用下产生一定的位移，带动坡脚左侧水平段管道也产生较大的Mises应力和弯矩；坡顶附近管道存在一处Mises应力极值点，主要由于该处竖向位移载荷较大，管道在竖向载荷和重力的共同作用下产生了较大的拉伸应力和弯矩。管道坡脚Mises应力分布和坡顶附近Mises应力分布如图6所示。

图6 管道Mises应力分布极值点Fig.6 Extreme point of Mises stress distribution in pipeline

分别对纵向穿越滑坡体管道施加离散滑坡位移和固定位移，比较两者有限元计算结果，前者管道最大Mises应力值比后者增大约50%，因此对管道施加离散滑坡位移进行受力分析的结论更加安全；虽然后者在坡脚弯管同样也出现了应力极值点，但是在坡脚左侧水平段、滑动面附近和坡顶附近管段均未出现应力极值点，主要由于对管道施加固定滑坡位移不能反映坡脚附近的滑动剪切作用及由此产生的影响，也不能反映坡顶竖向载荷比坡脚竖向载荷大对管道所产生的作用。

施加离散和固定滑坡位移条件下管道应力与弯矩的变化曲线如图7所示。由图7可看出：比较施加离散和固定位移条件下管道的弯矩分布，前者管道最大弯矩值比后者大1倍多，坡脚弯管两侧的弯矩最大，坡脚左侧水平段、滑动面附近和坡顶附近也存在弯矩极值点，说明坡脚弯管变形最剧烈，这在一定程度上也缓解了滑坡位移对管道的作用；弯管左侧水平段管道存在一处弯矩极值点，是由于坡脚弯管变形带动该点变形引起的；滑动面附件存在弯矩极值点，说明管道在剪切作用下产生了明显的局部弯曲变形；坡顶附近弯矩极值点是由于竖向滑坡位移分布不均使管道局部发生变形引起的。

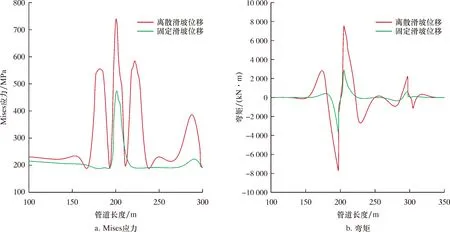
图7 离散和固定滑坡位移条件下管道应力与弯矩的变化曲线Fig.7 Variation curve of pipeline stress and bending moment under discrete and fixed landslide displacement

施加离散和固定滑坡位移条件下管道位移的变化曲线如图8所示。由图8可以看出：对穿越滑坡体管道施加离散滑坡位移时，管道在滑动面附近产生的水平位移最大，在坡脚弯管和坡顶弯管处产生的竖向位移较大，穿越滑坡体段管道总位移量相对于其两侧弯管位移量较小，沿坡顶固定土体段敷设的管道总位移量逐渐减小；对穿越滑坡体管道施加固定位移载荷时，管道产生的水平位移很小而竖向位移较大，穿越滑坡体段管道的竖向位移最大且基本不变，滑坡体两端固定土体内敷设管道的位移则逐渐减小。比较施加固定和离散位移条件下管道产生位移的最大值，前者比后者增大约17%，因此对穿越滑坡体管道施加离散滑坡位移，虽然管道产生的位移相对较小，但是在局部土壤剪切作用下管道的最大应力却较高；对穿越滑坡体管道施加固定滑坡位移，虽然管道产生的位移载荷较大，但是管道位移载荷分布较为均匀，不能体现局部土壤剪切作用下管道的受力状况，管道最大应力反而较小。

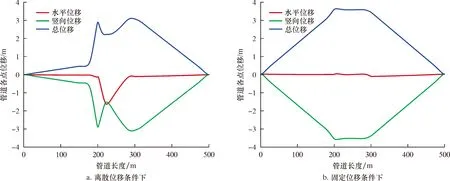
图8 离散和固定滑坡位移条件下管道位移的变化曲线Fig.8 Variation curve of pipeline displacement under discrete and fixed landslide displacement

内压和温差变化对纵向穿越滑坡体管道Mises应力影响如图9所示。

由图9可以看出：对穿越滑坡体管道施加离散滑坡位移，管道内压p由0逐渐增大到10 MPa，坡脚左侧水平段、坡脚弯管和滑动面附近管道Mises应力变化不大，坡顶附近Mises应力略有增加，增幅仅为7.3%，其余地段管道Mises应力均有明显增加，所以提高管道内压对坡脚左侧水平段、坡脚弯管和滑动面附近管道影响不大，因此对于纵向穿越滑坡体管道，其最大Mises应力主要由滑坡位移载荷引起；当管道温差ΔT由0增大到50 ℃时，由于管道沿线Mises应力分布基本不变，所以管道温差变化对纵向穿越滑坡体管道应力分布状况基本无影响。

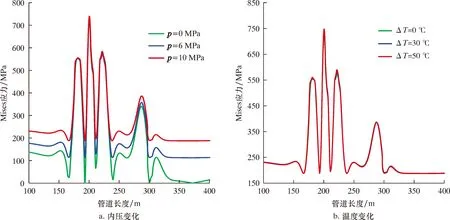
图9 内压和温差变化对纵向穿越滑坡体管道Mises应力的影响Fig.9 Effect of internal pressure and temperature difference variation on Mises stress of pipeline crossing sliding mass vertically

2.4 横向穿越滑坡体管道受力分析

当油气管道横向穿越滑坡体时，由于滑坡体上、中、下三个部位水平位移、竖向位移和总位移均不相同，所以横向穿越滑坡体上、中、下三个部位的管道受力状况也各不相同。滑动面以上区域沿坡顶至坡脚方向，水平滑坡位移逐渐增大，竖向滑坡位移却逐渐减小，总的滑坡位移量略有增加，如表2所示。

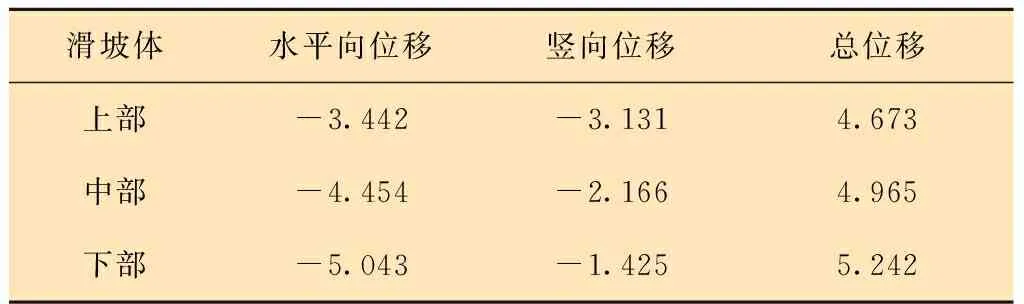
表2 滑坡体上、中、下部位的位移量 m

当管道横向穿越滑坡体不同部位时，需要根据穿越部位实际滑坡位移量对管道进行加载，虽然滑坡体上部总位移量相对较小，但是管道Mises应力却最大，滑坡体下部总位移量相对较小，但管道Mises应力却较小，主要由于管道本身具有一定的自重，竖向载荷对其影响更为明显，因此管道横向穿越滑坡体时易从滑坡体下部通过，虽然滑坡体下部水平位移和总位移量均较大，但管道Mises应力却较低。管道Mises应力最大值处于滑坡体与固定土体之间的交界面处，管道弯矩最大值处于交界面附近两侧，主要由于交界面两侧土体发生了较为明显的位移错动，导致穿越交界面处管道在土体剪切作用下产生较大的应力，交界面两侧管道同时也产生了较大的弯矩。横向穿越不同部位滑坡体管道应力和弯矩的变化曲线如图10所示。

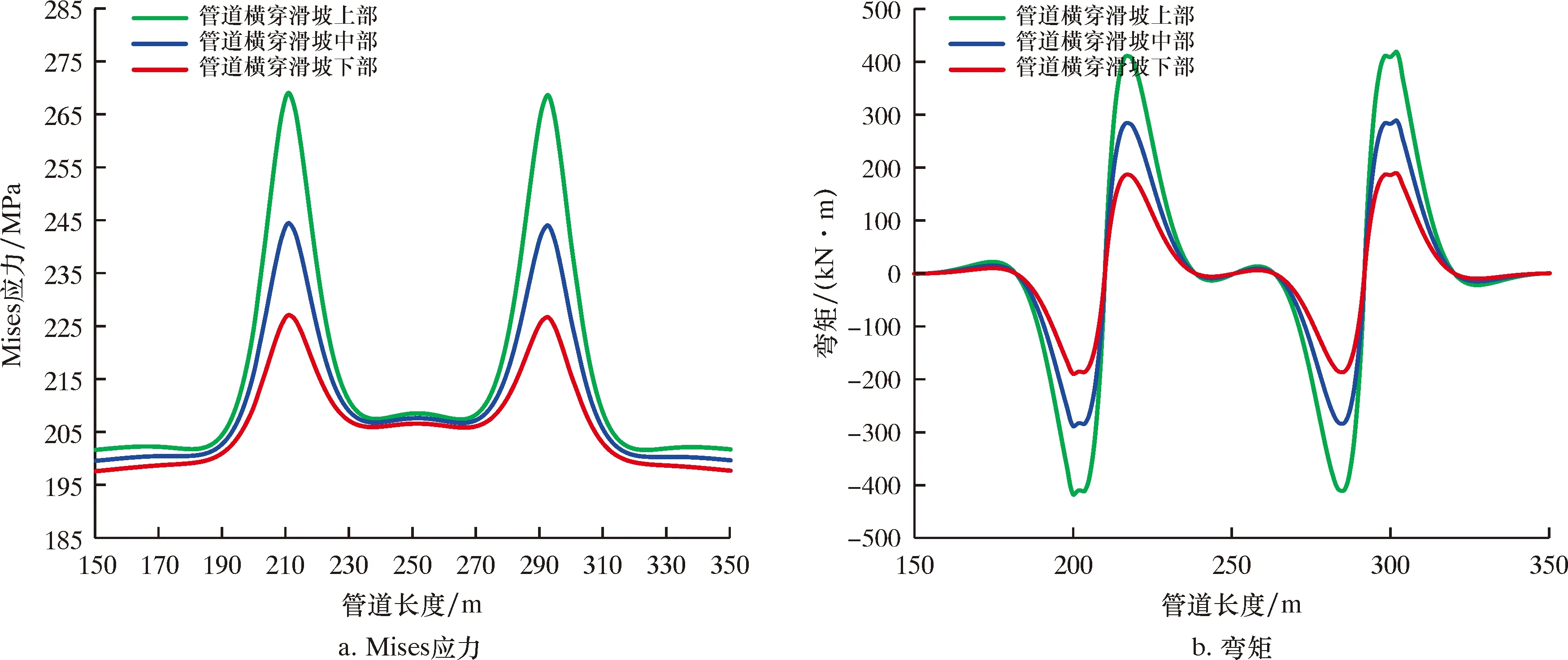
图10 横向穿越不同部位滑坡体管道应力和弯矩的变化曲线Fig.10 Variation curves of stress and bending moment of pipeline crossing different parts of sliding mass horizontally

当管道横向穿越滑坡体下部时，随着管道内压逐渐增大，管道Mises应力也逐渐加大，但是在滑坡体与固定土体交界面处，因滑坡位移产生的管道Mises应力占比却逐渐减小，例如案例中管道内压由0提高到10 MPa，因滑坡位移产生的管道Mises应力占管道总Mises应力比值由81%降低到9%，滑坡位移对管道应力的影响逐渐变得不明显，所以当管道横向穿越滑坡体时，高压管道受到滑坡位移载荷的影响较小，而低压管道受到的影响则较大。管道横向穿越滑坡体下部，随着管道温差逐渐增大，管道Mises应力也逐渐加大，尤其在滑坡体与固定土体交界面处，因滑坡位移产生的管道Mises应力占比也逐渐增大，例如案例中温差由0提高到50 ℃时，因滑坡位移产生的管道Mises应力占管道总Mises应力比值由2%增加到12%，所以当管道横向穿越滑坡体时，温差变化较大的管道受到滑坡位移载荷的影响更为明显。内压或温差变化对横向穿越滑坡体下部管道Mises应力影响如图11所示。

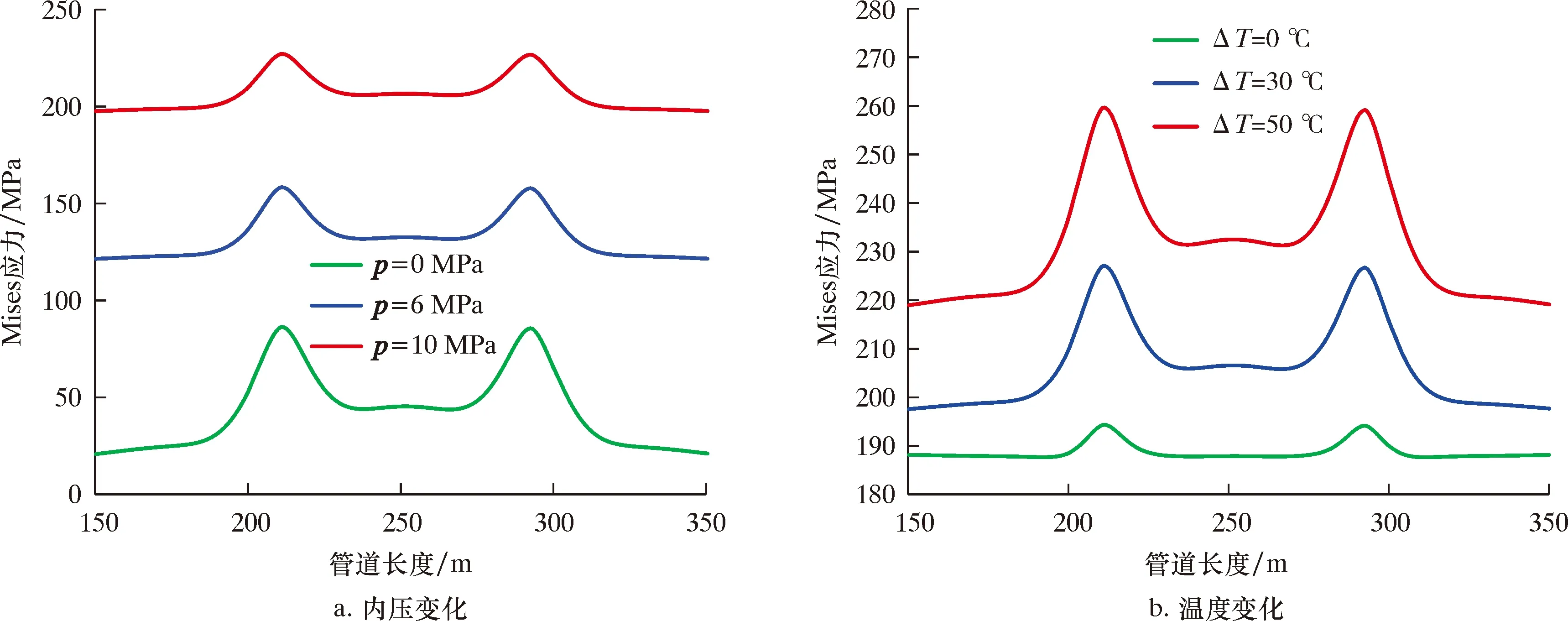
图11 内压和温差变化对横向穿越滑坡体下部管道Mises应力的影响Fig.11 Effect of internal pressure and temperature difference variation on Mises stress of pipeline crossing lower part of sliding mass horizontally

3 结 论

(1)基于离散滑坡位移条件下油气管道受力分析主要通过两步来实现，第一步采用有限元法求解滑坡体各点位移，通过逐渐降低坡体强度来实现坡体的滑动过程，当管道纵向穿越滑坡体时需要沿管道敷设方向提取坡体各点的滑坡位移，当管道横向穿越滑坡体时，需根据穿越坡体的不同部位来提取相应的滑动位移；第二步采用有限元建立管土作用模型，当管道纵向穿越滑坡体时，将沿管道敷设方向的离散滑坡位移载荷施加到对应位置的管道上，当管道横向穿越滑坡体时，将根据不同穿越部位所提取的滑坡位移施加到管道上，从而实现离散滑坡位移载荷作用下管道受力分析。采用该种方法对管道进行受力分析，计算结论可使管道更加安全。

(2)对于纵向穿越滑坡体油气管道施加离散滑坡位移，所得管道应力分布云图能够反映局部土体剪切作用对管道的影响，在坡脚左侧水平段、坡脚弯管、滑动面附近和坡顶附近共计4处产生了应力极值点，管道受力状况与滑坡体的滑动规律也更为相符，具有较好的适用性。纵向穿越滑坡体油气管道Mises应力最大值和弯矩最大值均位于坡脚弯管附近，坡脚左侧水平段和滑动面附近管道Mises应力值和弯矩值大致相当，坡顶附近管道Mises应力值和弯矩值进一步减小，因此坡脚弯管是纵向穿越滑坡体管道的防护重点。当内压逐渐增大时，纵向穿越滑坡体管道Mises应力极值点变化不大，其余段管道Mises应力均随着内压的增大而增大；温差变化对纵向穿越滑坡体油气管道受力基本无影响。

(3)当油气管道横向穿越滑坡体时，从滑坡体下部位置通过时管道Mises应力值较低，主要由于滑坡体坡脚附近的水平位移较大，而坡顶附近的竖向位移较大，同时考虑管道自身重力的影响，滑坡竖向位移载荷比水平位移载荷对管道的影响更明显。横向穿越滑坡体油气管道Mises应力极值点和弯矩极值点均位于固定土体和滑动土体的交界面处，呈对称分布，因此穿越交界面处的管道为防护重点。当油气管道横向穿越滑坡体时，低压管道相对于高压管道受滑坡位移的影响更为明显，而温差变化较大的管道比温差变化较小的管道更易受到滑坡位移的影响。