管道全位置焊缝三维测量研究*

胡曦 余震 刘海生

(1.武汉科技大学机械自动化学院 2.湖北文理学院机械工程学院)

0 引 言

传统的焊缝测量方法是靠人工接触式测量，效率低，工人劳动强度大，达不到工业自动化要求。目前已有通过视觉手段对焊缝尺寸进行非接触式测量的方法[1]。文献[2-5]使用激光视觉法，向焊缝表面投射激光条纹，通过图像处理提取条纹中心线，结合相机标定参数，计算特征点空间坐标进行焊缝三维测量。文献[6]采用2台带660 nm窄带滤波器和850 nm长通滤波器的摄像机，通过图像配准对焊接熔池进行三维重建，并提出了一种基于焊缝熔池图像轮廓的在线焊缝成形前焊缝宽度预测方法，采用高斯分布拟合等高线的像素宽度和三维重建测得的对应焊缝宽度。针对管道测量，有通过探头对管道内径的接触式测量方法，也有激光检测法和超声波法等非接触式测量方法[7]，它们均通过在管道截面提取几个点来检测管道截面的变形情况。对于管道三维检测，文献[8] 利用表面形貌测试仪对套管磨损表面的参数进行测量，通过对数据进行处理可恢复套管磨损表面三维形貌图。文献[9]研究了基于NURBS曲面的管道表面三维重建算法，重建出管道局部变形表面，可直观地了解管道变形情况。文献[10]建立了内压作用下三维管道环焊缝缺陷仿真模型，分别对不同韧性参数、管道及缺陷尺寸进行了研究，模拟计算得出各变化参数下管道的拉应变极限和失效压力。研究管道焊缝的变化规律，可为管道环焊缝缺陷完整性评价提供理论指导。

本文采用机器视觉手段对管段全位置焊缝进行三维测量。因激光视觉法需要投射结构光，易受环境影响，且进行激光扫描三维重建时还需高精度运动控制台，系统较复杂，而使用双目视觉手段，标定后只需立体匹配，结合视差便能对视野范围内所有目标进行同步测量，效率较高。因此，选择使用双目立体视觉，针对管道全位置MAG盖面焊缝，定义焊缝余高和宽度测量方法，将其按空间位置分为8个焊缝区，分别对每个区间焊缝余高和宽度进行三维测量分析。

1 双目立体视觉测量系统

1.1 测量系统构成

双目立体视觉系统由2个CCD相机、光源、计算机和工作台支架组成，如图1所示。2个相机安装在可调支架上，其距离、高度和角度都可调节。将管道焊缝分成8个区域，用相机对各个区域重构实现管道全位置焊缝三维测量。

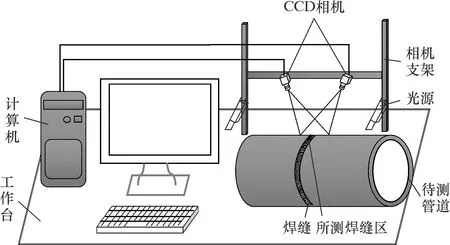
图1 系统示意图Fig.1 Schematic diagram of system

1.2 双目立体视觉测量原理

双目视觉通过从不同视角获取被测物体的两图像，结合视差原理[11]恢复物体表面的深度信息，实现对目标的三维测量，其测量模型如图2所示。图2中，OL、OR分别为左右相机光心，两者距离为基线距b，f为焦距。空间中任意一点P通过立体匹配得到左右像平面上的坐标为Pl(xl，yl)，Pr(xr,yr)，计算该点的视差，通过相似三角测量法便可得P点的三维坐标。

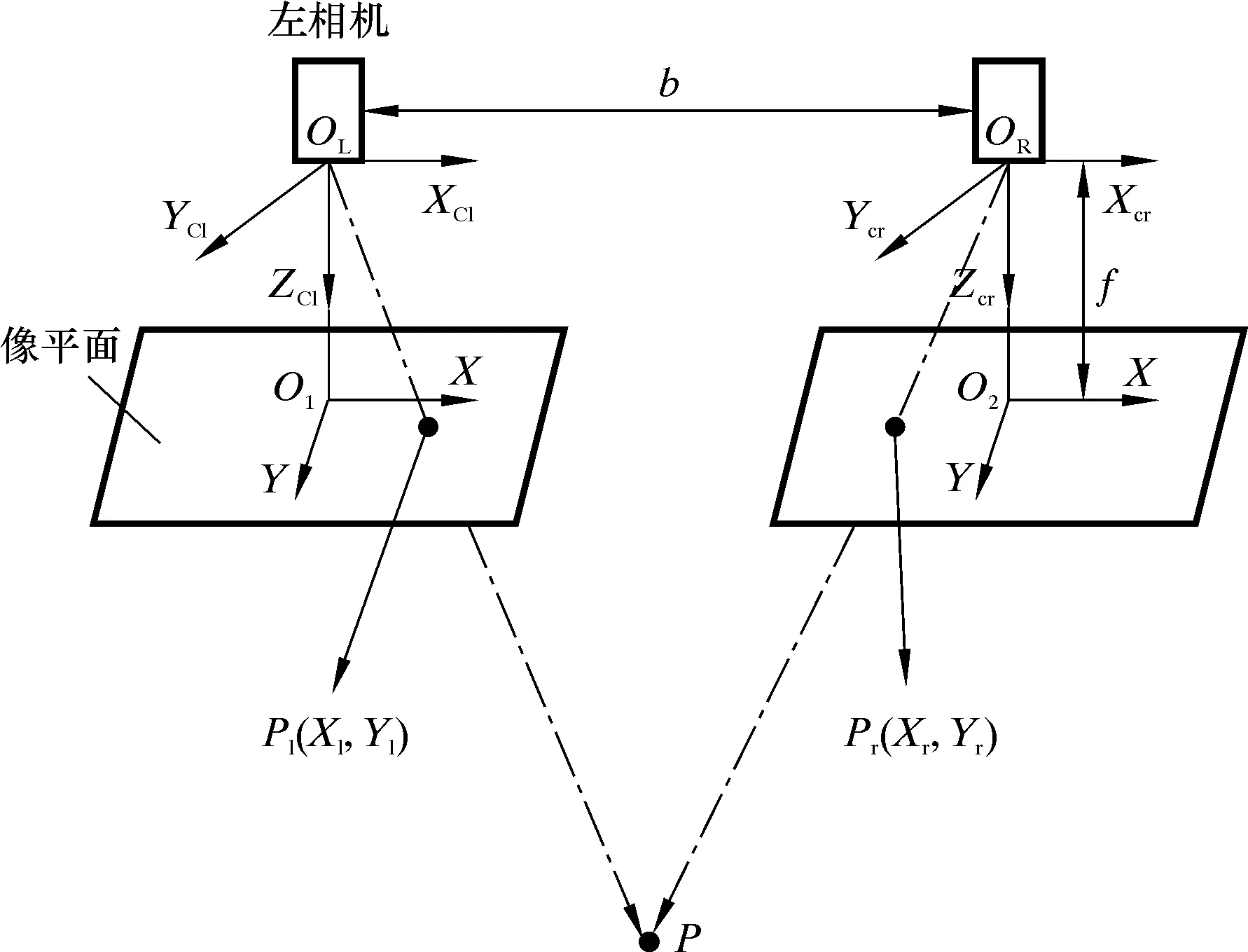
图2 双目视觉测量模型Fig.2 Binocular vision measurement model

2 双目标定及立体匹配

2.1 双目标定

采用张正友平面标定法[12]来进行双目相机的标定，使用圆点标定板拍摄多幅不同角度及位置的标定板图像，精确提取各标定板圆点的圆心坐标，根据各坐标之间的相互对应关系，先不考虑畸变，计算相机内外参数的初始值，再考虑畸变，进行畸变和极线校正，最终得出校正后的两相机内外参数。

相机成像过程中投影变换涉及4个坐标系之间的转换。设相机坐标系为Oc-xcyczc，世界坐标系为Ow-xwcwyw，图像坐标系O-xy，像素坐标系为O-uv，空间中任意一点(Xw,Yw,Zw)投影到图像中的像素坐标为(u,v)，则具体转换如下：

(1)

式中：u0、v0为主点中心坐标；K为相机内参数矩阵；R为旋转矩阵，T为平移向量，分别表示从世界坐标系到摄像机坐标系的旋转和平移变换，即相机外参。

式(1)为单目视觉数学模型，双目标定还需要获得两相机之间的相对位置关系。假设有一空间点在世界坐标系和左右两摄像机坐标系下的非齐次坐标分别为nw、n1、n2，则有：

(2)

消去nw可得：

(3)

式(3)即为左右相机坐标系的相对位置关系。定义R21、T21分别为右相机相对左相机的旋转矩阵和平移向量，则有：

(4)

式中：R1、T1、R2、T2分别为左右像机外参数，可由单相标定分别求出，R21、T21分别为左、右相机的相对位置参数。

2.2 立体匹配

立体匹配是通过构建能量代价函数将两幅视图联系在一起，找到空间一点在左右视图中的同名点，根据这两个同名点坐标差计算视差。传统的立体匹配算法(SSD、SAD、NCC)构建的函数仅与像素点的灰度值有关，通过建立匹配窗口，计算左右图像窗口内像素点灰度值的相关性进行匹配，获取的视差图可能不连续。此次试验所构建的能量函数不仅与待匹配点的灰度值有关，而且还结合该点的灰度值梯度以及邻域的平滑因子，因此获取的视差图连续且平滑。能量函数如式(5)所示。

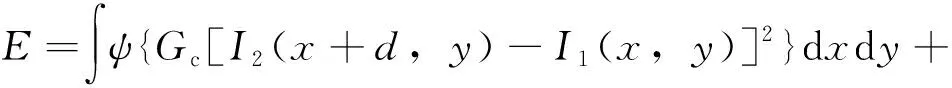
(5)

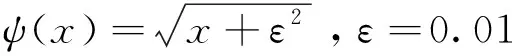
立体匹配搜索原理如图3所示。在图3的左视图中一待匹配点Pl，沿该点极线在右视图一定范围内搜索匹配点，某个点与该点的构成能量函数值最低，则此两点为同名点，求两个点x坐标之差即为视差值，依此方法遍历全图即得到视差图。

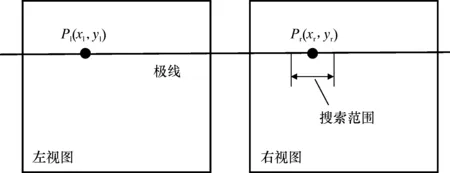
图3 匹配原理图Fig.3 Matching principle graph

2.3 空间点三维坐标计算

空间一点P在左像平面坐标为(xl，yl)，通过立体匹配找到其在右像平面坐标为(xr,yr)，经极线校正后两点处于同一行，即yl=yr，且视差d=xl-xr，通过三角测量法由图4可推导出以下关系式：

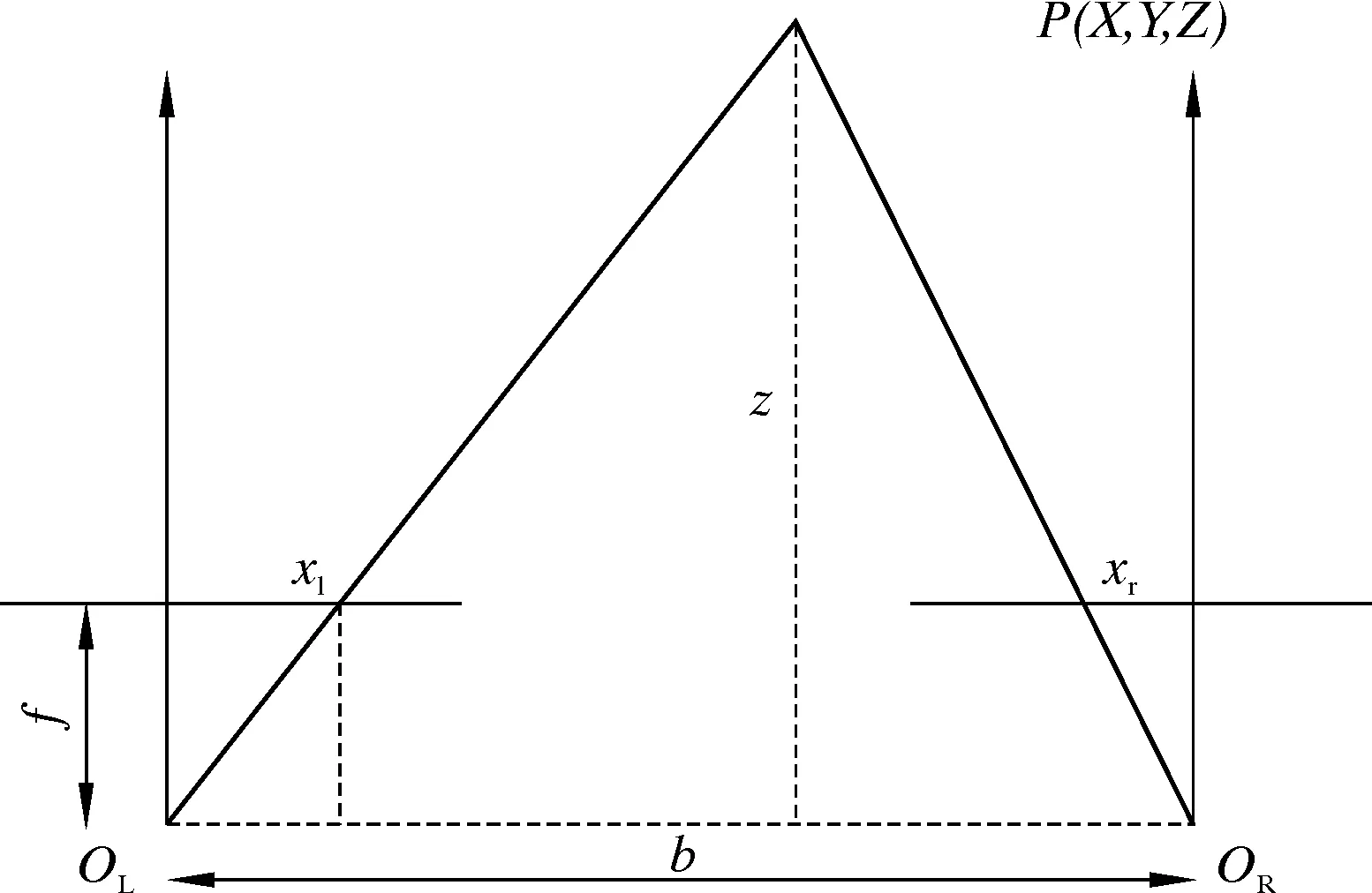
图4 视差模型图Fig.4 Parallax model

(6)

(7)

从式(6)和式(7)可知，只要通过立体匹配找到空间点在左右像平面上的投影点，计算视差，就可求出该点三维坐标，依此遍历便可获得三维点云，完成重构。

3 焊缝三维重构试验

3.1 试验系统搭建及标定

设计的双目视觉测量系统由2个大恒工业相机、光源LED灯、计算机、工作台及相机支架组成。相机型号为MER-500-14GM/C-P ，分辨率为2592(H)×1944(V)，像素尺寸2.2 μm×2.2 μm，镜头焦距16 mm。将2相机调整好高度和角度并固定在支架上。由于测量对象为管道盖面焊焊缝，待测范围较窄，故设计2台相机横向距离约120 mm，相机距待测物体表面距离为400～500 mm，其采集的图像传输给计算机用于实时图像处理。在管道下方两侧的三角固定件上有滑轮，便于管道旋转进行全位置测量。测量系统实物图如图5所示。

图5 测量系统实物图Fig.5 Actual measurement system

先对系统进行标定，采用7×7(50 mm×50 mm)高精度实心圆阵列标定板，圆心距为6.25 mm。将标定板在两相机下方旋转和平移多次，共采集20张处于不同角度和高度的标定板图像，通过标定和校正后两相机内外参数如表1和表2所示。

表1 左右相机内参数Table 1 Internal parameters of left and right cameras

由表2可见畸变系数为0，即已完成畸变校正，且两相机主点中心列坐标相同，右相机相对左相机仅在X方向有平移，距离约117 mm，与设计距离(120 mm)很接近，因此极线校正已完成。

表2 校正后右相机相对左相机位置Table 2 Pose of right camera relative to left camera after correction

3.2 焊缝三维重构

采集管道部分弧度范围的焊缝图像，使用标定数据对其进行极线校正后，如图6a所示，然后通过形态学处理提取焊缝区域，采用2.2节构建的能量函数匹配计算，得到连续平滑的视差图，如图6b所示。

图6 焊缝图像Fig.6 3D measurement results

视差图中越暗的部分表示该处离相机越近，因为采集的是管道部分弧度的焊缝，视差图下半部分是管道上表面离相机较近部分，所以从图6b中可看到从下到上逐渐由暗到亮。遍历各点视差(视差图中各点灰度值)，根据式(6)和式(7)计算三维坐标，导出焊缝点云图，如图7所示。由重建后的焊缝三维模型图可以看出，焊缝成鱼鳞状，焊缝高度明显。

图7 重建后的焊缝三维模型Fig.7 Reconstructed 3D model of welding seam

3.3 三维测量精度分析

为验证双目测量精度，随机选取8组标定板图像。标定板摆放位置及倾斜角度各不相同(即距离相机位置不同)，提取各组标定板的任意相邻两个标志点圆心P1P2，如图8所示，重构三维坐标，将两点圆心距与标准值(6.25 mm)做比较，分析重构精度，结果如表3所示。从表3可以得出，三维重构精度误差在0.2 mm内。

图8 标定板图像Fig.8 Calibration board image

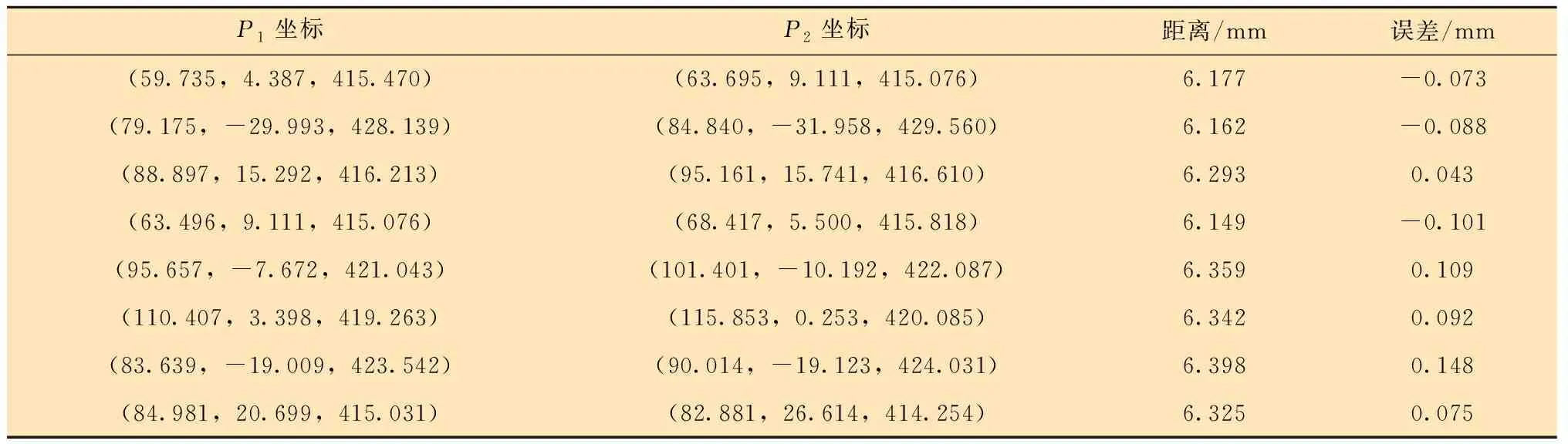
表3 三维测量结果Table 3 3D measurement results

4 管道全位置焊缝三维测量分析

4.1 焊缝宽度和余高测量

研究对象为管道盖面焊焊缝，先按照第2、第3节方法进行三维重构焊缝，获取焊缝表面所有点云坐标，然后提取焊缝边缘点，将最高点作为特征点，根据特征点三维坐标计算如图9所示的余高和焊宽。

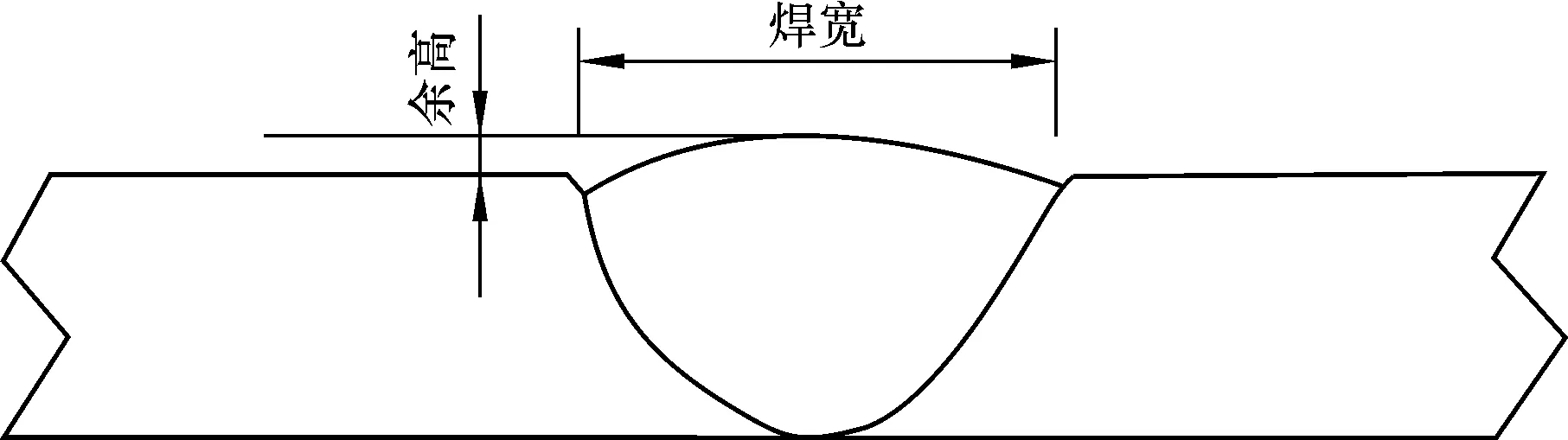
图9 焊缝尺寸图Fig.9 Weld size

焊缝宽度：在要测量的焊缝段横向提取(y坐标相同)边缘点，假设提取的焊缝左右两端边缘点为P1(x1，y1，z1)，P2(x2，y2，z2)，则两边缘点的欧几里得距离即为焊宽W，如式(8)所示：

(8)

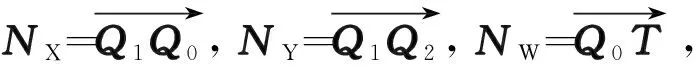
(9)

再求该平面的单位法向量z=NZ/|NZ|=(i,j,k)，此时单位法向量z与向量NW的数量积即为点T到平面Q0Q1Q2的垂直距离HT：

HT=Z·NW=(i,j,k)·
(x3-x0,y3-y0,z3-z0)

(10)

设提取了n个焊缝最高点，各点与管道表面点构成的向量为(xm，ym，zm)，依次求其高度再取平均值作为该段焊缝的余高H，具体如式(11)所示：

(11)

4.2 全位置焊缝三维测量分析

针对管道全位置盖面焊焊接，在使用智能焊接小车焊接时，按空间位置不同将管道分为如图10所示的8个区间，各区间的焊接工艺参数见表4。在试验时用记号笔标记好管道各区间位置，通过三维重构各区间焊缝，实现管道全位置焊缝宽度和余高的三维测量。

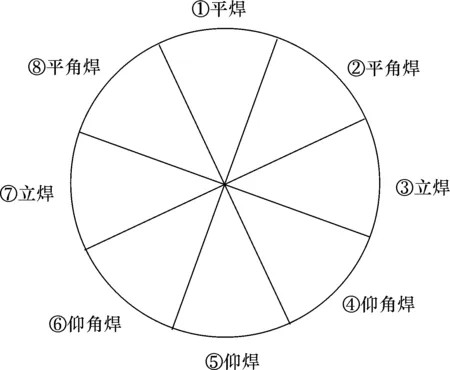
图10 焊缝区间图Fig.10 Weld area

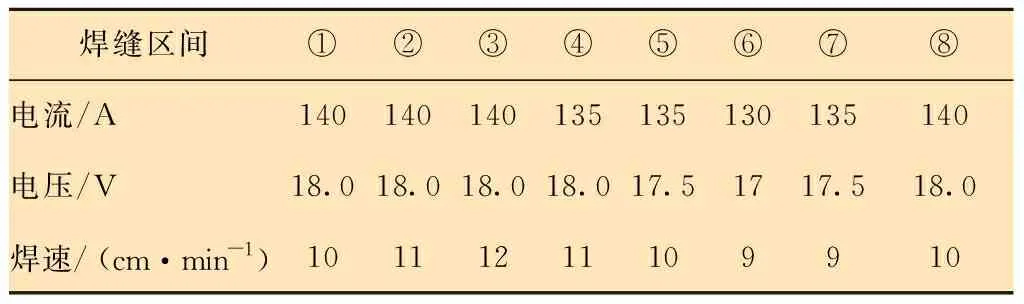
表4 焊接工艺参数Table 4 Welding parameters

先对管道各区间焊缝进行重构：通过管道两侧下方的三角滑轨使管道旋转到标记好的区间位置，以便双目相机能扫描到指定区间焊缝，然后对该段焊缝进行重构，获得表面所有点云坐标，并按照4.1节方法提取特征点坐标，计算余高和焊宽。依次对每个区间进行计算，各区间取5组数据，结果如图11所示。

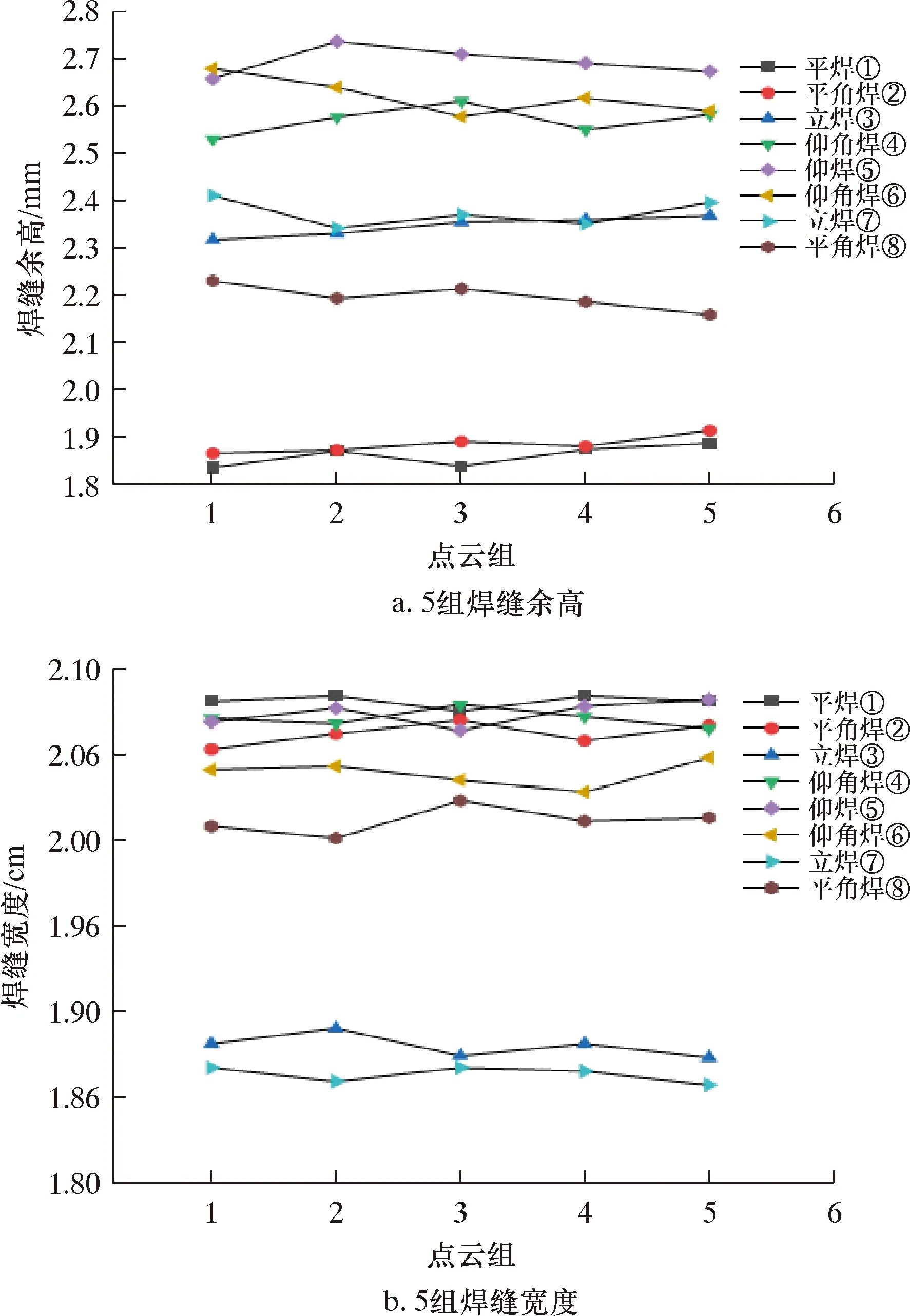
图11 5组焊缝尺寸Fig.11 Sizes of 5 groups of welding seams

对5组数据取平均值作为该区间余高和焊宽，结果如表5所示。

表5 焊缝尺寸 mm

为了便于观察分析，对各区域所获得的焊缝点云运用贪婪算法[13]进行三角曲面拟合，得到的三维模型如图12所示。

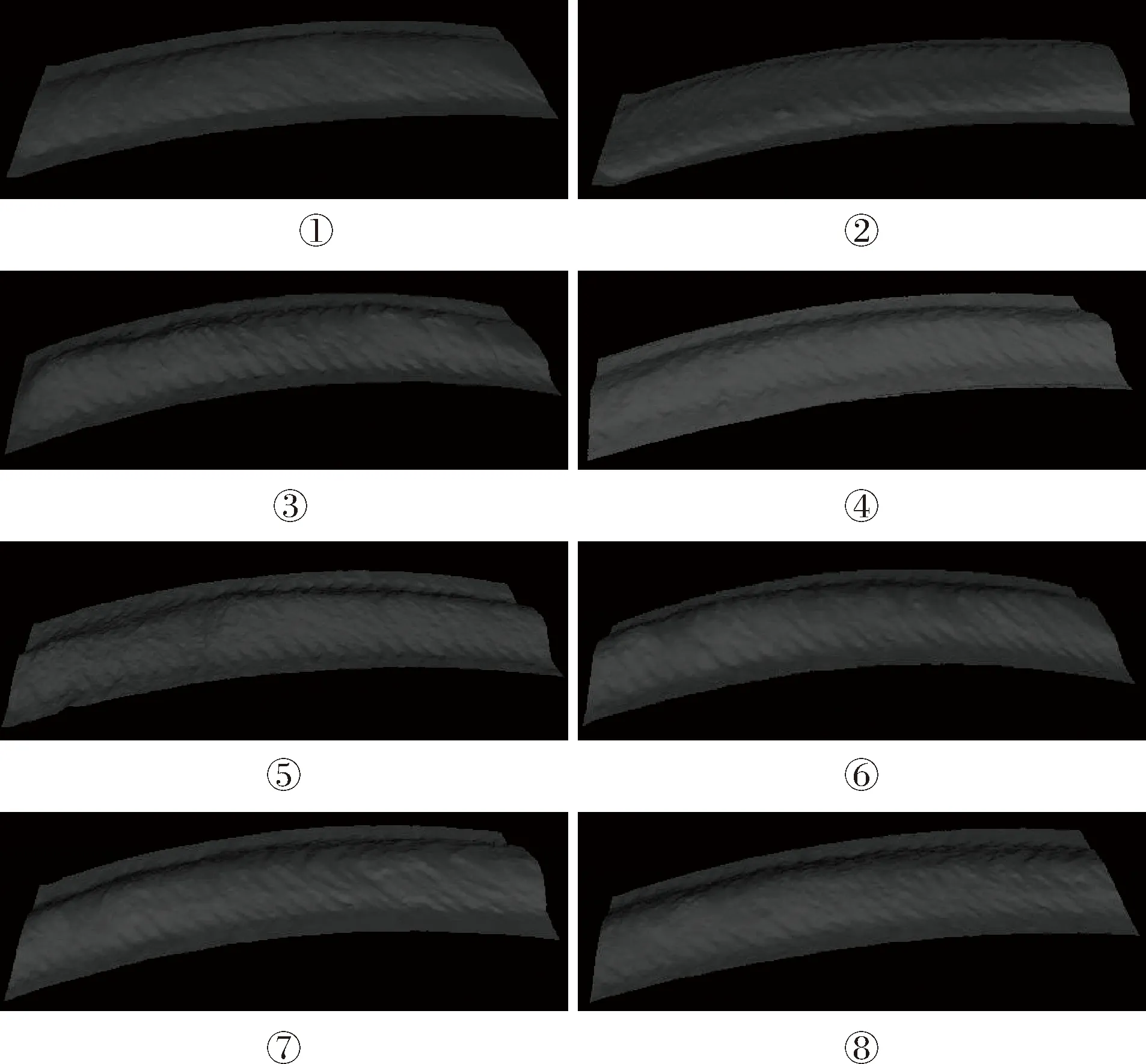
图12 全位置焊缝三维重建模型Fig.12 3D reconstruction model of all-position welding seams

从图12和表5可得：在平焊区间①时，焊缝处于水平位置，焊接时熔池流动平缓，比较容易控制，因此焊波表面较平坦，分布较均匀，焊缝表面很平整，焊缝余高较小。

在平角焊区间②和⑧时，由于②处于下坡焊位置，熔池两侧熔融金属均沿坡中间向下流淌，在电弧压力作用下，形成凹液面，故焊缝中间有点凹陷，焊缝余高也较小。在处于⑧上坡焊区间时，由于上坡角度变化，熔池内金属会向下流入尾部，电弧能更一步深入到熔池底端，因此熔深增加，并且余高也相对于平焊缝增加。

在处于③向下立焊区间时，因为重力作用，熔池里熔化金属容易下淌，可能分离导致焊缝不平整，表面焊波较粗，并且在焊接时，焊接速度相对较快，故焊缝宽度相对较窄。在区间⑦对应的向上立焊中，由于从下往上焊接，电流电压都有所减小，焊接速度控制较慢，且因为熔池重力向下而电弧牵引力向上，熔池被拉长，所以焊波弧度变小，焊缝也较窄。

在④、⑤和⑥的仰焊区间时，熔池处于管道下表面，没有焊材金属承托，熔化金属容易脱落下坠，所以焊接时电流和电压相对较小，焊接速度相对较慢，每次向熔池过渡的金属不会太多。由于熔池形状不易控制，焊波分布不均匀，焊道也因重力作用呈现出中间较凸、两边较低的形状，导致焊缝表面凹凸不平，余高较大。

5 结 论

(1)采用平面模板法对双目相机进行标定和校正，构建与匹配点灰度值、灰度值梯度以及邻域的平滑性有关的能量函数，并使用多重网格迭代算法进行匹配计算得到焊缝视差图，由视差图生成稠密点云，进而得到焊缝三维重建结果。

(2)提取多组不同位置标定板的圆心点坐标，计算相邻两点的圆心距离，并将其与标准值做比较，验证三维重构精度误差在0.2 mm以内。

(3)定义了焊缝宽度和余高计算方法，将管道焊缝按焊接空间位置不同分为8个区域，进行了全位置三维重构，提取各区间特征点坐标进行了三维测量焊缝余高和宽度，并结合各区间焊接工艺参数及三维模型进行了分析。

(4)研究结果表明，所设计的方法能实现焊缝尺寸的在线测量，精度较高。全位置三维测量测得平焊缝余高较小，立焊缝宽度较窄，而仰焊缝焊道较凸，余高较大。