基于梯度域引导滤波的视差精炼迭代算法
朱程涛,李 锵
(天津大学微电子学院,天津 300072)
立体视觉是从两个或多个视点观察同一景物,以获取在不同视角下的感知图像,通过三角测量原理计算图像像素点间的视差来获取景物的三维信息[1].现阶段,该技术已广泛应用于众多领域,如立体显示、场景重建[2]、行人检测等.立体视觉技术主要涉及到摄像机标定、图像矫正、立体匹配、三维重建等步骤,其中立体匹配是最重要也是最困难的步骤,其主要目的是通过相应的算法获取参考图像与目标图像之间对应匹配点间的关系,生成相应的视差图,视差图中每一个像素点的灰度值代表了该点与对应匹配点间的坐标差信息.
现阶段常用的立体匹配算法通常建立在Sharstein等[1]提出的理论框架基础之上,立体匹配的步骤主要分为:①初始匹配代价的计算;②匹配代价的聚合;③视差的计算;④视差精炼.
在初始匹配代价的计算阶段,常用的有 AD、GRAD[3]、Census变换[4]等匹配代价.匹配代价的聚合阶段是众多立体匹配算法改进的重点之一,主要有基于窗口的算法[5-8]以及基于图像滤波的算法[9-11].
传统的立体匹配算法大多针对于初始匹配代价计算以及匹配代价聚合阶段进行改进,Ma等[12]指出视差精炼算法的性能直接影响着立体匹配的精度.传统的视差精炼方法主要是采用简单的邻近视差填充的方法[1],此类方法一般能消除较多的误匹配点的视差值,因此使用得较多,但视差精炼的精度有限.Rhemann等[13]提出了基于权重中值滤波的方法大大地提升了视差精炼的精度,其主要是根据图像滤波算法对待精炼的视差图进行加权滤波,以达到精炼误匹配点视差的目的.
基于权重中值滤波的视差精炼方法中使用的滤波算法性能直接影响到视差精炼的精度,因此采用滤波性能优良的算法用以改进视差精炼的精度显得尤为重要.Ma等[12]采用引导滤波算法[14]提升了视差精炼的精度.引导滤波算法是图像滤波领域内常用的滤波算法.然而,引导滤波算法本身存在一定局限性,尤其在图像边缘处存在一定的滤波缺陷.而一些针对引导滤波的改进算法被不断提出,具有代表性的有 Li等[15]提出的权重引导滤波算法 WGIF,以及Kou等[16]梯度域引导滤波算法 GDGIF.其中,GDGIF算法取得的滤波性能优于GIF、WGIF等具有代表性的滤波算法[16].
本文将 GDGIF与权重中值滤波相结合,运用于立体匹配的视差精炼阶段.对得到的精炼视差图进行迭代精炼,根据迭代前后的差异信息对视差做进一步的优化,以获得更高精度的精炼效果.
1 传统的视差精炼算法
在传统立体匹配中,分别以左、右图为参考图像,经过立体匹配算法得到左图初始视差图、右图初始视差图后,需要采用左右一致性检测(LRC)[1]剔除视差图中的误匹配点
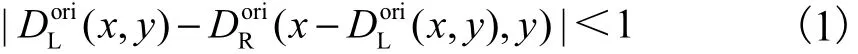
满足式(1)的点为好点;不满足此条件的点为误匹配点,应予以剔除.视差精炼算法是针对误匹配点进行有效视差填充从而得到匹配精度更高的视差图.
传统的视差精炼方法[1]通常采用简单填充的方式,即用离误匹配点最近的好点对误匹配点pocc进行填充,填充后的视差值为,其计算式为
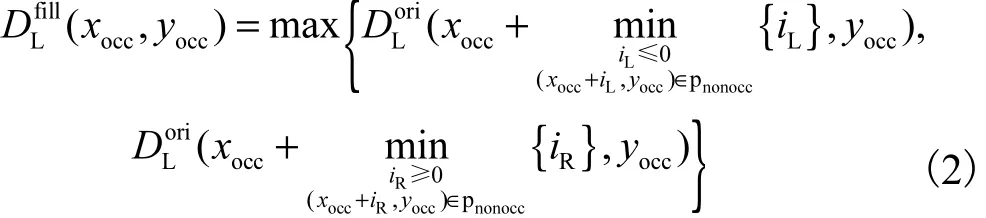
上述方法可以在一定程度上提高匹配的精度,但提升的精度有限.一种较为有效的改进方式是对得到的进行权重中值滤波,即为误匹配点邻近的好点赋予不同的权重,并与中值滤波相结合得到较为合理的精炼结果[12].
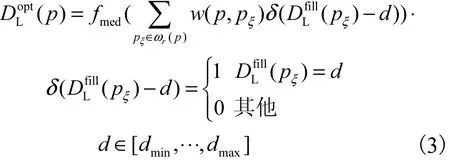
式中:pξ代表以p为中心,矩形窗口ωr(p)(半径为r)内的任意像素点;d代表视差搜索集合内的任意视差值;dmin、dmax分别代表最小、最大视差值;w(p,pξ)代表p、pξ两点之间的权重;fmed代表中值滤波操作.
2 本文算法
为了获得高精度的视差精炼效果,本文将梯度域引导滤波与中值滤波算法相结合,对立体匹配算法得到的视差图进行迭代精炼.
2.1 权重中值滤波的改进
梯度域引导滤波GDGIF算法具有良好的保边缘特性[16].在 GDGIF中,滤波输出Q与输入引导图像I在限定的窗口内满足一定的线性关系,即为
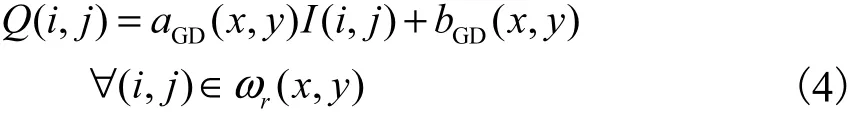
式中:(i,j)代表以(x,y)为中心点像素、窗口 ωr(x,y)内的任意像素点;aGD(x,y)、bGD(x,y)为滤波参数.
为求得最佳滤波参数(x,y)和(x,y),Kou等[16]构建了一个能量方程 E(aGD(x,y),bGD(x,y)),使其达到最小化时即可求得滤波参数.
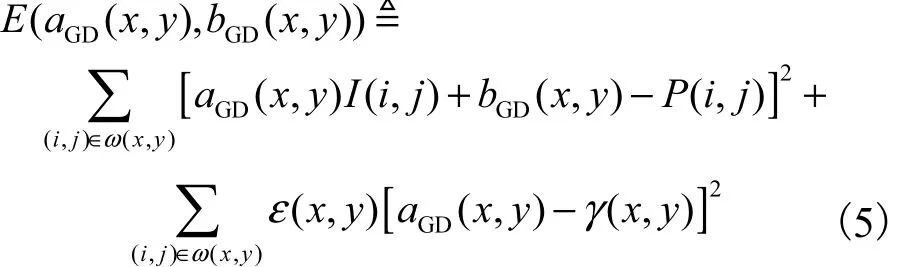
式中:P代表待滤波的图像;γ(x,y)的定义与引导图像结构有关;ε(x,y)是为了避免aGD(x,y)变化过大而设置的正则化参数,ε(x,y)值越大滤波强度越大,反之越小.
Kou等[16]同时指出由于GIF中ε(x,v)采用固定值,使得 GIF滤波效果受到限制,通过分析图像的结构特征,不同区域的像素点应赋予不同的ε(x,y)值,即在图像平坦区域的像素点应具有较大的ε(x,y)值,边缘区域的像素点应具有较小的ε(x,y)值,从而达到较好的保边缘效果.
本文根据 GDGIF的原理,对每个视差层图像进行GDGIF滤波,首先构建每层视差层图像的能量函数,即
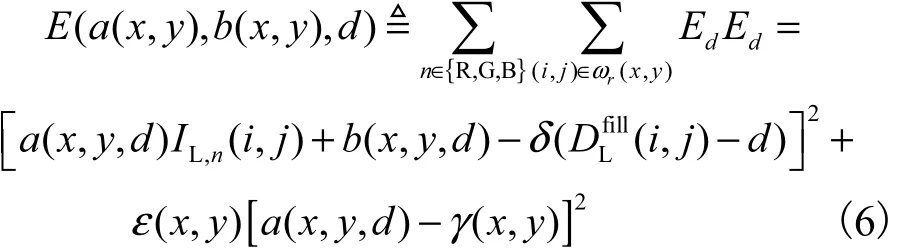
式中:IL,n代表左图(包含 3个 RGB通道n∈{R ,G,B}),将其作为引导图像;a(x,y,d)、 b(x,y,d)为滤波参数;依据GDGIF原理,ε(x,y)、γ(x,y)定义[16]为
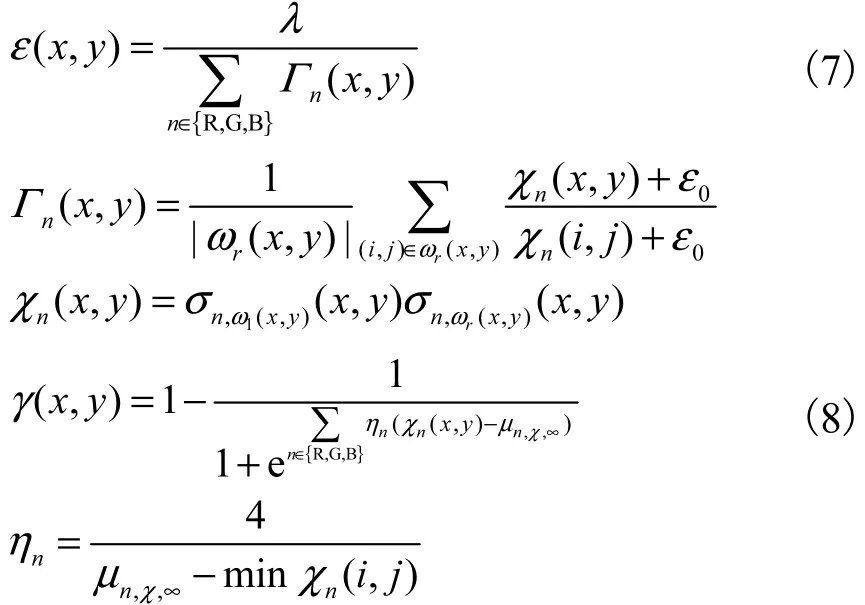
式中:ε0、λ为常数;Γn(x,y)代表图像 IL,n的结构信息;|ωr(x,y)|代表窗口ωr(x,y)(半径为r)内的总像素数 ;σn,ω1(x,y)、σn,ωr(x,y)分 别 代 表 图 像 IL,n在 窗 口ω1(x ,y)、ωr(x,y)内的标准差;μn,χ,∞代表χn(i,j)在窗口ωr(x,y)内的平均值,即
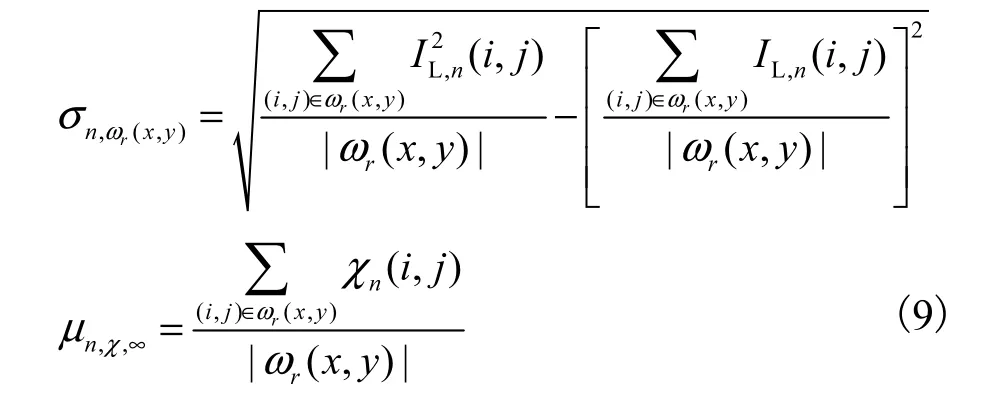
为求得最佳滤波参数 a*(x,y,d)和b*(x,y,d),使式(6)达到最小化时即可求得滤波参数.

式中:μ(x,y,d)、μ(x,y)分别代表 δ(Dfill(i,j)-
P;LI;L,nL d)、IL,n(i,j)在窗口ωr(x,y)内的均值;(x,y)代表IL,n(i,j)在窗口ωr(x,y)内的方差;即

因此图像的 GDGIF滤波输出结果 H(i,j,d)的表达式为
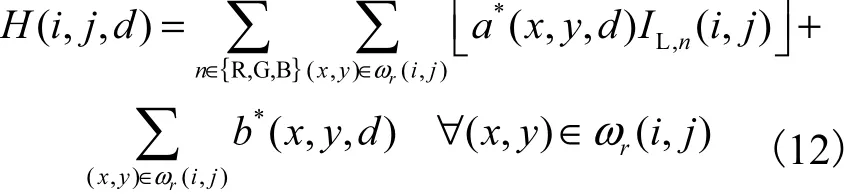
在 GDGIF滤波模型中,由式(7)计算得到的ε(x,y)可知,图像平坦区域的像素点具有较大的ε(x,y)值,因此滤波程度较强;边缘区域的像素点具有较小的ε(x,y)值,因此滤波程度较弱;而GIF滤波模型中ε(x,y)值为一常数.由上述分析可知GDGIF的保边缘特性强于GIF.
在得到 H(i,j,d)之后,即可统计(i,j)邻域内的累加滤波输出

根据式(14)即可得到像素点(i,j)进行视差精炼后的视差值,即

2.2 视差精炼的迭代
在根据上述基于GDGIF原理得到精炼后的左视差图后,对重复视差精炼过程,依次得到迭代精炼后的视差图和.如图1所示为对 Middlebury[17]提供的测试图 Teddy图像使用传统的窗口聚合算法[1]得到未精炼的视差图后,采用本文算法进行视差精炼迭代的示意.表 1为视差精炼迭代过程的误匹配率实验数据对比,误差阈值取为1,其中 Nonocc、All、Disc分别表示非遮挡区域、总区域、深度不连续区域.
比较得出第2、3次精炼过程中视差值产生变化的像素点pc,即
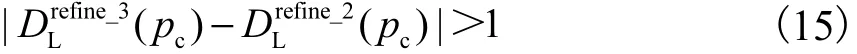
对于像素点pc的视差需要做进一步的精炼,通常此类误匹配点在做第1次视差精炼时未被检测出,只有通过后面的迭代精炼过程才有可能被检测出来.
图 1(e)所示的黑色像素点为第 1次精炼后的图1(b)在第 2次精炼后的图 1(c)中被视为好点的点,视差值未被精炼,但在第 3次精炼后的图 1(d)中这些区域的视差被精炼了,而图 1(e)正是由图 1(c)和图1(d)经过式(15)检测得到.

图1 视差精炼迭代示意Fig.1 Schematic of the disparity refinement algorithm
采用基于权重中值滤波的视差精炼方法并不是迭代次数越多精度越高,过度的迭代则会导致一些好的像素点的视差值在精炼后发生错误.由表 1可知,第 3次迭代精炼的 All区域误匹配率为 12.67%,,高于第2次迭代精炼的12.35%,.
为避免过度迭代产生的不良后果,本文拟采用滤波求均值的方式对式(15)检测得到的误匹配点进行修正,而不是直接采用更多次数迭代的精炼方法.

式中:w(p)为窗口N(pc)内 GDGIF滤波的权重;标志位矩阵M(p)定义为
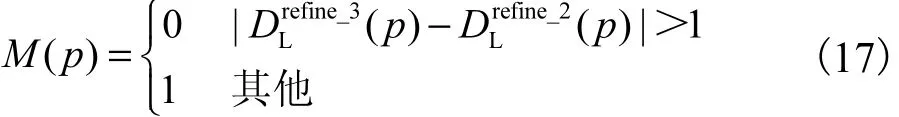
最终得到的视差精炼结果为.
图 1(f)所示为采用式(16)、(17)得到的最终视差精炼效果图,与图 1(c)相比较,小熊头部上端的错误视差值得到更正.通过比较误匹配率可知,本文精炼方法得到的误匹配率最低,如在 All区域内的误匹配率为 12.15%,,低于 refine_2阶段的 12.35%,以及refine_3阶段的12.67%,.

表1 视差精炼迭代过程的误匹配率比较Tab.1 Comparison of error rates with the iteration times%
图2所示为本文算法流程,待精炼视差图经过 3次(基于梯度域引导滤波的)权重中值滤波后得到相应阶段的精炼结果,再依据式(15)~式(17)进行滤波求均值计算后即可得到最终的视差精炼结果.
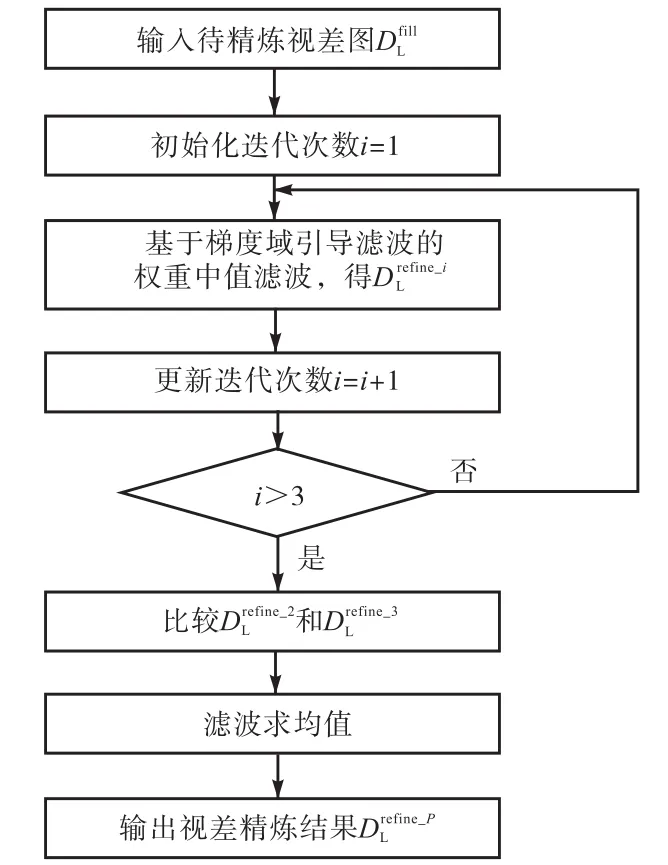
图2 本文算法流程Fig.2 Flow chart of the proposed algorithm
3 仿真实验结果及对比分析
本文利用 MATLAB编程实现所提算法及相关对比算法.实验中使用的计算机硬件配置为 Intel Core i7-3610,QM CPU,8,GB内存.仿真实验所用测试图及标准视差图来源于 Middlebury-Version 2(http://vision.middlebury.edu/stereo).
在仿真实验中,本文算法主要参数设置为
图 3所示为采用传统的窗口聚合算法[1]进行立体匹配得到未精炼的视差图后,采用不同算法获得的视差精炼效果对比.

图3 不同方法获得的视差精炼效果对比Fig.3 Comparison of disparity refinement maps with different methods
图 4所示为对 Venus精炼结果进行局部放大后的效果对比,其中图 4(a)中红色矩形框所包含区域为对比的区域.表 2是各算法之间的误匹配率实验数据对比,误差阈值取为 1.表 3是各算法之间的运行时间对比.
由图 3以及表 2可知,传统立体匹配方法得到的初始视差图存在较多的误匹配点,算法平均误匹配率高达 15.68%.文献[1]中的算法采用简单的邻近像素视差值对误匹配点的视差进行填充,精炼后的视差图存在明显的填充痕迹,如Teddy图小熊附近.
采用双边滤波中值滤波方法的算法[13]较为明显地提高了匹配的精度,如Tsukuba在All区域的误匹配率由文献[1]中的算法的 6.03%,降低至 3.11%,Venus在 All区域的误匹配率则由 3.20%降至0.76%.文献[12]中的算法采用的引导滤波对视差进行精炼,其滤波性能优于双边滤波,得到的视差精炼精度优于文献[13]中的算法,平均误匹配率为6.87%.
在Teddy视差图中,本文的迭代精炼算法较好地消除了小熊左边区域的误匹配视差,在 Disc区域的误匹配率为 18.46%,低于文献[12]的算法的20.11%.本文算法在Cones的All区域内的匹配性能好于文献[12]的算法,图中筷子所在区域存在误匹配的现象是因为传统立体匹配方法算法性能较差,致使得到的初始视差图精度不高.
在经过迭代精炼后,本文算法得到的视差图看上去较为自然,得益于 GDGIF的保边缘特性,视差图的边界区域保留的较为完整,如图4所示的Venus的前景区域,未精炼的视差图在上述区域存在较多的误匹配现象,相较于文献[1]、文献[13]和文献[12]的算法,本文算法在这一区域获得的精炼效果最佳,边界得到较好的保留.
通过对比误匹配率,使用传统的基于窗口聚合的立体匹配算法进行立体匹配,得到的初始视差图存在较多的误匹配现象,经由本文视差精炼算法进行精炼后,得到的平均误匹配率仅为6.25%,.
由表 3可知,文献[1]的算法采用简单的方式进行视差精炼,其运行时间最短.而本文算法由于需要进行迭代运算,故其运行时间较长.

图4 实验结果局部放大对比Fig.4 Comparison of close-up refinement results

表2 不同算法的误匹配率比较Tab.2 Comparison of error rates of different algorithms%

表3 不同算法的运行时间比较Tab.3 Runtime comparison for benchmark stereo images
4 结 语
本文依据 GDGIF滤波算法,将其与权重中值滤波方法相结合,对立体匹配方法得到的初始视差图进行迭代精炼,得益于 GDGIF滤波的优良性能,本文算法对于视差精度的提升具有一定的效果,实验结果表明了本文算法的可靠性.
[1]Sharstein D,Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J].International Journal on Computer Vision,2002,47(1):7-42.
[2]何 凯,朱程涛,姚静娴. 基于双权重聚合的立体匹配算法[J]. 吉林大学学报:工学版,2015,45(4):1318-1323.He Kai,Zhu Chengtao,Yao Jingxian. Stereo matching algorithm based on double weighting aggregation[J].Journal of Jilin University:Engineering and Technology Edition,2015,45(4):1318-1323(in Chinese).
[3]de Maeztu L,Villanueva A,Cabeza R. Stereo matching using gradient similarity and locally adaptive support weight[J].Pattern Recognition Letters,2011,32(13):1643-1651.
[4]周 龙,徐贵力,李开宇,等. 基于 Census 变换和改进自适应窗口的立体匹配算法[J]. 航空学报,2012,33(5):886-892.Zhou Long,Xu Guili,Li Kaiyu,et al. Stereo matching algorithm based on census transform and modified adaptive windows[J].Acta Aeronautica et Astronautica Sinica,2012,33(5):886-892(in Chinese).
[5]Zhang K,Lu J,Lafruit G. Cross-based local stereo matching using orthogonal integral images[J].IEEE Transactions on Circuits and Systems for Video Technology,2009,19(7):1073-1079.
[6]Gu Z,Su X,Liu Y,et al. Local stereo matching with adaptive support-weight,rank transform and disparity calibration[J].Pattern Recognition Letters,2008,29(9):1230-1235.
[7]Kehtarnavaz N. Stereo matching via selective multiple windows[J].Journal of Electronic Imaging,2007,16(1):1-14.
[8]何 凯,王晓文,葛云峰. 基于 SIFT描述子的自适应聚合权重立体匹配算法[J]. 天津大学学报:自然科学与工程技术版,2016,49(9):978-983.He Kai,Wang Xiaowen,Ge Yunfeng. Adaptive support-weight stereo matching algorithm based on SIFT descriptors[J].Journal of Tianjin University:Science and Technology,2016,49(9):978-983(in Chinese).
[9]Min D,Lu J,Do M N. Joint histogram based cost aggregation for stereo matching[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(10):2539-2545.
[10]Yang Q. Stereo matching using tree filtering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2015,37(4):834-846.
[11]Heo Y S,Lee K M,Lee S U. Robust stereo matching using adaptive normalized cross-correlation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(4):807-822.
[12]Ma Z,He K,Wei Y,et al. Constant time weighted median filtering for stereo matching and beyond[C]//IEEE International Conference on Computer Vision.Sydney,Australia,2013:49-56.
[13]Rhemann C,Hosni A,Bleyer M,et al. Fast costvolume filtering for visual correspondence and beyond[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Colorado Springs,USA,2011:3017-3024.
[14]He K,Sun J,Tang X. Guided image filtering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(6):1397-1409.
[15]Li Z,Zheng J,Zhu Z,et al. Weighted guided image filtering[J].IEEE Transactions on Image Processing,2015,24(1):120-129.
[16]Kou F,Chen W,Wen C,et al. Gradient domain guided image filtering[J].IEEE Transactions on Image Processing,2015,24(11):4528-4539.

