基于极坐标系下二维直方图的图像分割算法

张 军，张治恒，朱新山

(天津大学电气自动化与信息工程学院，天津 300072)

图像分割是图像处理中的关键技术之一，也是人工智能领域中的一项基础工作.针对图像分割的理论研究已经持续了几十年，期间陆续提出了很多分割算法.这些算法的原理不尽相同，有基于阈值的分割方法、基于边缘的分割方法、基于区域生长的分割方法以及基于特定理论的分割方法[1].其中，基于阈值的分割方法操作简单，在图像分割中应用非常广泛.

基于阈值的图像分割方法的关键在于最优阈值的选取.最大类间方差法[2](Otsu法)是由日本学者提出的一种经典阈值分割方法，它利用图像的灰度分布一维直方图进行分割阈值的选取，在图像受噪声干扰较小时分割效果较为理想，但是由于只利用了图像的灰度信息，在图像受噪声干扰严重时，分割效果非常差.针对一维直方图易受噪声干扰的问题，二维直方图受到学者们的关注.二维直方图不仅仅利用图像灰度信息，还考虑图像的空间信息，例如引入像素点的邻域灰度均值概念，以区分噪声点和非噪声点，算法的抗噪性得到了提升.

Pun[3]于20世纪80年代最先提出利用信息论中熵的概念进行图像分割，此后，基于各种类型熵的图像分割算法被陆续提出.相较于其他类型熵，Khehra等[4]发现 Renyi熵在图像分割算法中分割性能更好.Sahoo等[5]将二维直方图和 Renyi熵结合起来进行图像分割，取得了较好的分割效果.

将 Renyi熵和二维直方图结合起来进行图像分割的算法在精度上虽然更高，但是由于在寻找最优阈值对的过程中需要遍历整个二维直方图，算法运算量非常大，无法满足实时性要求；基于传统二维直方图的图像分割方法通过阈值对将二维直方图划分为 4个区域，取处于对角线的2个区域而忽略远离对角线的另外2个区域的做法必然会引起误分的情况，阈值的选取也出现偏差；另外，基于传统二维直方图的图像分割方法建立在图像噪声点较少的假设下，所以处理信噪比较小的图像时效果较差.

针对基于传统二维直方图的阈值分割算法存在的问题，本文提出基于极坐标系下二维直方图的阈值分割方法，将像素点灰度值信息和空间信息表示在极坐标系中，以便更好地对所有像素点进行处理.实验结果表明，该算法在分割精度和速度方面都有明显提高.

1 传统二维直方图阈值分割算法存在的问题

设图像大小为×MN，像素点灰度值为f(x,y)，其灰度级数为L.对图像各像素点求取其×kk邻域的灰度均值 g(x,y)为

式中k为邻域算子的尺寸，一般取奇数.显然，g(x,y)的灰度级数也为L.

记 f(x,y)和 g(x,y)组成的二元组为(i,j)，其中，0 ≤ i,j ≤ L - 1，二元组(i,j)出现的频数为 cij，相应的概率为 pij，则有 pij= cij/(M N)，且满足

传统二维直方图定义在一个×LL大小的正方形区域中.假设阈值对(t,s)将该正方形区域划分为 4部分，如图1中0～3区所示.

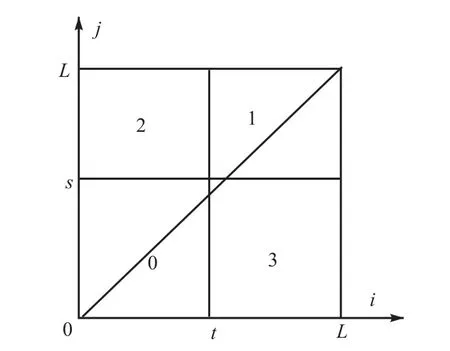
图1 二维直方图区域划分Fig.1 Region partition of two-dimensional histogram

图像中目标和背景内部的像素点灰度分布较均匀，其灰度值 f(x,y)和邻域均值 g(x,y)非常接近；而噪声点和边界点的灰度值与其邻域均值相差较大，因此，背景点和目标点主要分布在二维直方图的对角线附近，对应图 1中的区域 0和区域 1；噪声点和边界点则分布在远离对角线的区域，对应图1中的区域 2和区域3.

假设对角线上的区域 0和区域 1分别对应于目标和背景，远离对角线的区域2和区域3对应于边缘和噪声.由于噪声点和边界点通常只占少数，为简化计算，一般认为在区域2和3上所有的Σpij=0.记0和1所对应的目标和背景2个区域分别为 c1和 c2，则这两类的先验概率分别为

由于噪声点和边界点数量较少，所以满足

图像的α 阶二维Renyi 熵定义为

式中α＞0且α≠1.二维Renyi 熵阈值法的最优阈值取(t*,s*)为

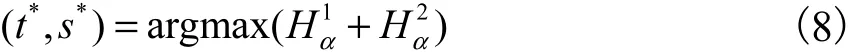
式中0 ≤t,s≤L- 1.

在上述求取最佳阈值的过程中，主要的工作是Renyi熵的计算.从式(3)、(4)和式(6)、(7)可以看出，对每一个阈值(t, s)，其二维 Renyi熵的计算都要从像素点(0,0)开始累加，计算量为 O ( L2)，共有 L2个(t, s)，因此总的计算量为 O ( L4)，其迭代运算量巨大，无法满足实时性要求.

根据这种区域划分方法计算最佳阈值时，还会出现误分情况，如图2所示.对于区域0中c、d两部分及区域 1中 a、f 两部分内的像素点来说，其灰度值和邻域均值相差较大，应属于边界点或噪声点，但传统二维直方图阈值分割方法将其直接分类为目标(或背景)内点；同时，区域 2、3中靠近对角线的 b、e两部分，其内部像素点的灰度和邻域灰度均值相近，应属于目标或背景内点，但却被看作噪声点或边界点.因此，基于这种直方图区域划分计算得到的最佳阈值必然会出现偏差.另外，区域2、3中像素点所占比例近似为 0，这一假设在图像受噪声污染较严重时是不成立的，所以传统算法无法很好地处理含噪图像.

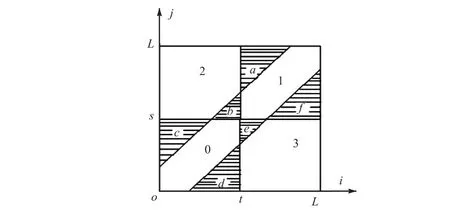
图2 二维直方图区域误分示意Fig.2 Region misclassification of two-dimensional histogram

针对传统基于二维直方图的图像阈值分割方法存在的问题，近年来各种改进算法不断被提出，龚劬等[6]提出基于分解的二维 Renyi熵图像阈值分割算法，通过分解思想降低算法维度；潘 喆 等[7]、Yimit等[8]提出快速二维 Renyi熵阈值分割算法，通过分析二维 Renyi熵最佳阈值求解公式，推导出其递推公式，达到快速求解的效果；Cheng等[9]提出结合分解思想和模糊理论以达到速度和精度兼顾的算法；El-Sayed等[10]提出将求解域限定在二维直方图对角线上以减少计算量；Zheng等[11]提出二维灰度-局部方差直方图，将求解域压缩为 256×64以减少计算量；Zhang等[12]用递归的思想处理二维运算以降低计算量.这些算法都在一定程度上降低了利用二维 Renyi熵求取最佳阈值的算法复杂度.,雷博[13]、黄金杰等[14]、Xiao等[15]对传统二维 Renyi熵算法做了部分改进，以减少误分概率；Gu等[16]采用改进的粒子群优化算法结合二维 Renyi熵以增强算法的鲁棒性；Fan等[17]将二维 Renyi熵和模糊理论结合起来以处理具有过渡区的图像，处理效果良好.

2 基于极坐标系下二维直方图的图像阈值分割算法

2.1 极坐标系下二维直方图的构建

针对传统二维直方图阈值分割算法存在的以上问题，提出一种基于极坐标系下二维直方图的图像分割算法，基本思想如下.

对于原灰度图中每一像素点(x,y) ，都有对应的灰度值 f(x,y) 和邻域均值 g(x,y) ，g(x,y) 定义为

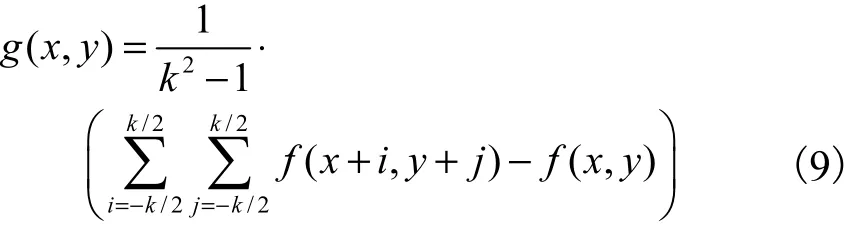
之所以不采用式(1)中定义的 g ( x, y)，是为了使噪声点的灰度值和邻域均值之差更加明显，以便于后续去噪过程的进行.

由 f ( x, y)和 g ( x, y)定义像素点(x, y)在极坐标系中的参数.设每一像素点(x, y)在极坐标系中的极径为ρ(x, y)，极角为θ(x, y)，具体定义为

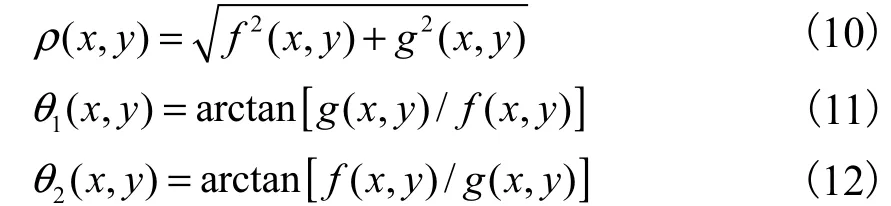
f( x, y)和g( x, y)的灰度级都为L，则极径ρ(x, y )的范围为，极角θ(x,y) 的范围为[0,/2]π.根据反正切函数的性质可知，1θ(x,y) 、2θ(x,y) 之间满足

由式(11)和式(12)所示的两个极角定义对像素点类别进行判定的变量Δ(x,y) 为

因为1θ(x,y) 和2θ(x,y) 之间满足式(13)所示关系，根据三角函数性质，(x,y) Δ又可写为

对于目标区和背景区来说，其内部灰度分布较均匀，每一像素点的灰度值和邻域均值差别很小，其比值也非常接近于1，所以1θ和2θ都近似为45°，二者差值Δ也近似为 0°；对于噪声点和边界点来说，其灰度值和邻域均值相差较大，相应地，1θ和2θ的差值Δ也将很大，尤其是灰度值很小的暗噪声点，1θ和2θ的差值Δ甚至会达到/2π，而边界点相对于噪声点来说，其灰度值和邻域均值之差一般要小于噪声点，相应地，边界点的Δ也小于噪声点的Δ.根据1θ和2θ的差值Δ可很好地判断出像素点的类别.将像素点分为两类，其中，背景点和目标点为1C，噪声点和边界点为2C，则有判别公式

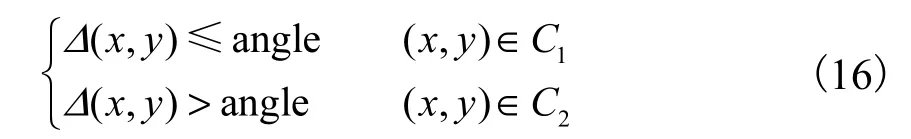
式中 angle是对像素点进行类别判定的阈值，可根据图像的性质进行选择.

在对测试图像每一个像素点的Δ进行计算并统计后，可以发现接近于 0°的Δ所占比例非常大，而较大的 0°所占比例较小，这说明在一幅图像中，目标和背景点是主要组成部分，边界点和噪声点只是少数.

基于图像的这一特点，可根据以下步骤间接求解类别判定阈值angle：

(1)根据式(12)和式(15)计算所有像素点的极角之差Δ(x, y)，并统计Δ(x, y)的分布，从0°到90°排列，得到所有的角度之差Δ(x, y)的可能性以及每个Δ(x, y)出现的频数.

(2)由于噪声点和边界点的Δ(x,y) 较大，且比例较小，所以可以设定比例阈值K，表示背景点和目标点所占的比例，如 90%=K ，从Δ=90°开始，将每个对应的频率相加，哪个Δ先到达比例阈值K，就认为该Δ是所求的判定阈值angle.

(3)对受噪声污染较小的图片，比例阈值K可设置的大一些，受噪声污染较大的图片，则K可设置的小一些，以后续的滤波效果图为准则，选取较为理想的比例阈值.

以添加密度为 0.02的椒盐噪声的 Lena图为例进行说明，求得所有像素点的极角差Δ(x,y) 的分布，如图 3所示，选取 90%=K 以求取类别判定阈值angle，最终求得 angle=16.2°.

图3 Lena噪声图极角差分布Fig.3 Polar angle differences distribution of Lena noise image

在用 angle对原图像各像素点进行类别划分后，即可得到边界点和噪声点.对这部分像素进行处理，达到滤噪的目的.本文所采取的处理措施是选取噪声点和边界点的邻域均值代替其灰度值.仍以添加密度为0.02的椒盐噪声的Lena图进行说明，对比其滤噪前后的效果图和极坐标系下的二维分布，如图 4所示.

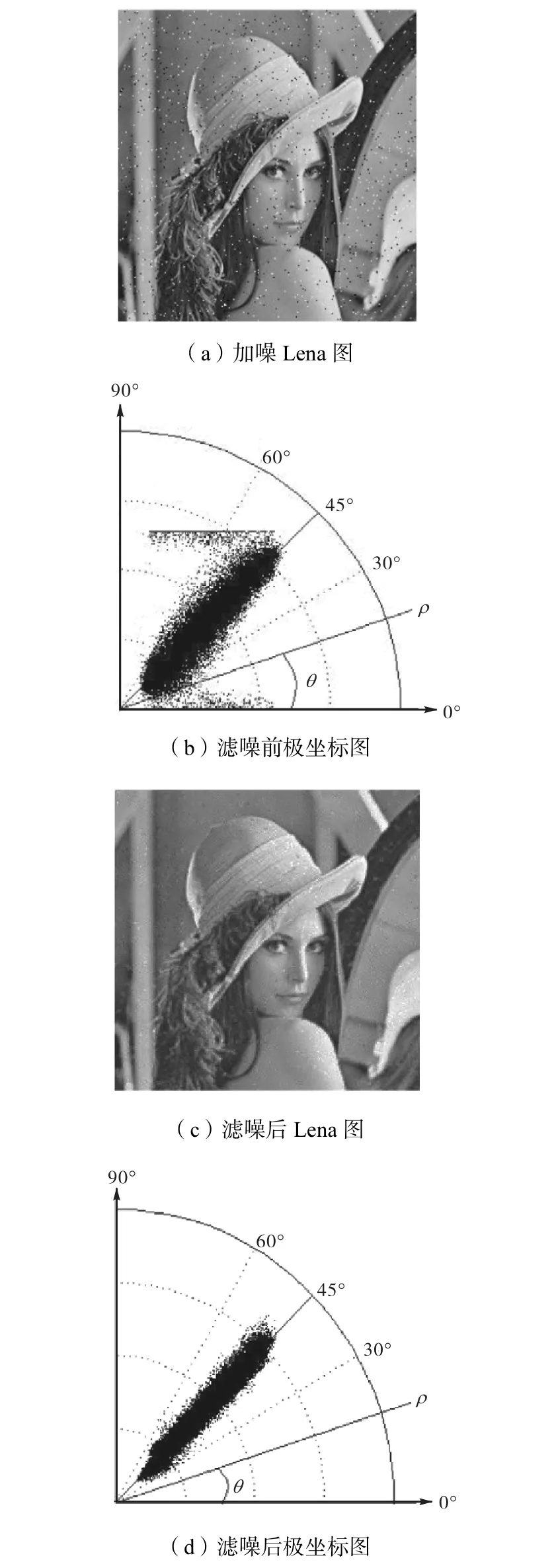
图4 图像滤噪前后对比Fig.4 Comparison of images before and after filtering

由图 4(a)、(c)可以看到，图像中的噪声点得到了比较良好的处理.

经过上述滤噪处理后，在极坐标系中原本分布散乱的像素点都将集中分布在极坐标系中极角为45°的极径附近，如图 4(b)、(d)所示.利用图 4(d)中像素点的分布即可求得最优分割阈值.

2.2 基于Renyi熵的阈值分割算法

本文利用 Renyi熵对去噪后的图像求取最佳阈值.将去噪后的图像各像素点都映射到极坐标系中，统计极坐标系中极角范围.假设去噪后图像所有像素点的极角范围为[45°-β，45°+α]，其中α和β都是很小的偏差值，例如在第 2.1节中对加噪 Lena图求得的像素点类别判定阈值 angle=16.2°，根据式(15)可求得去噪后像素点的极角为45°＋8.1°.因此，某像素点究竟属于目标点还是背景点将取决于它的极径.可以利用去噪后图像各像素点的极径信息结合Renyi熵概念，求取最佳阈值T，将图像分为目标区O和背景区B，以此实现对图像的分割.该过程如图5所示.

假设阈值为 t，用 t去划分去噪后的图像极径信息.认为极径小于等于 t的像素点属于目标区O，而极径大于 t的像素点属于背景区 B，根据Renyi熵的定义得到目标区和背景区所对应的Renyi熵为

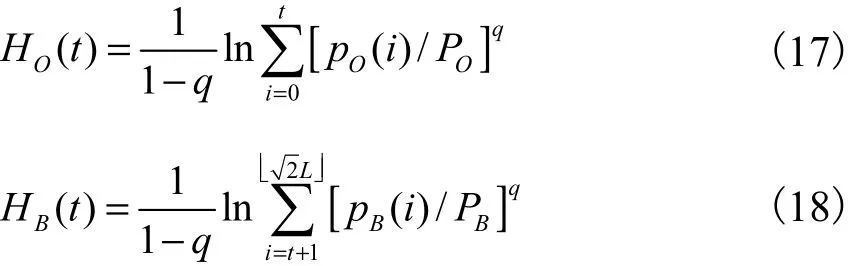
式中：表示向下取整；pO(i)代表位于目标区的极径为 i的像素点的概率；pB(i)代表位于背景区的极径为 i的像素点的概率；PO为目标区像素点的比例；PB为背景区像素点的比例；q为 Renyi熵的阶数，q＞0且q≠1.

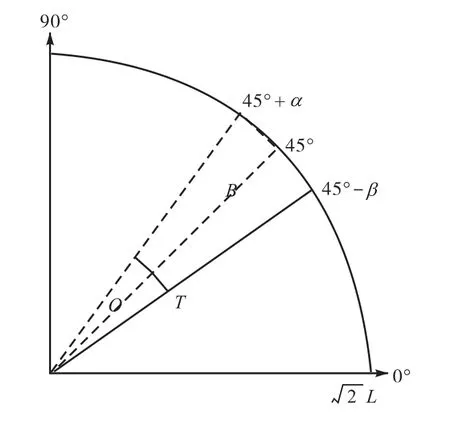
图5 极坐标系下分割算法示意Fig.5 Sketch map of segmentation algorithm in polar coordinate system

图像Renyi熵 H ( t)为目标区Renyi熵 HO(t)和背景区Renyi熵 HB(t)之和，则最佳阈值T定义为

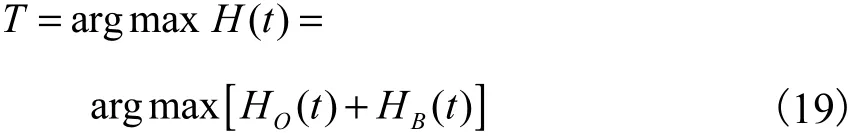
由于本文提出的算法将图像信息集中在极坐标系 45°极径附近，各像素点的极角差异很小.为简化计算，可忽略极角参量，只利用极径信息对各像素点进行分类，这属于一维问题，相较于基于传统二维直方图的阈值分割方法，其运算量大大降低.

本文算法主要包含以下几个步骤.

步骤 1 根据原始图像各像素点的灰度值分布f( x, y)求取其邻域均值，得到邻域均值信息 g ( x, y).

步骤 2 由灰度信息 f( x, y)和邻域均值信息g( x, y)，根据式(11)和式(12)对图像每一像素点求取其极角θ1(x, y)和θ2(x, y).

步骤3 根据每个像素点的两个极角差(x,y) Δ判断该像素点的类别.

步骤 4 对属于噪声或边界的像素点进行滤噪处理.本文选取噪声点和边界点的邻域均值代替其灰度值.根据处理之后的图像效果，调整步骤 3中用到的比例阈值，直到滤噪后的图像质量明显改善为止.

步骤 5 对处理后的图像再次求取每一点的邻域均值、相应的极径、极角等信息.此时所有像素点的极角基本都分布在45°左右，偏差很小.

步骤 6 根据各点极径信息，利用一维 Renyi熵求取最佳分割阈值，并利用该阈值对图像进行分割，得到二值化图像.

3 实验结果与分析

本文实验在系统配置 2.96,GB内存、2.30,GHz，Matlab R2014a下进行，挑选 Lena图、Cameraman图、Cat图、Corn图、Bird图为测试图片，如图6(a)所示，分别对比了传统二维 Renyi熵分割算法[5]、基于二维 Tsallis熵的分割算法[10]、基于灰度-局部方差二维 Renyi熵分割算法[11]、改进的灰度-梯度二维Renyi熵分割算法[14]以及本文算法 5种算法的分割效果图，如图 6(b)～(f)所示；对比原图在 5种算法下求得的最优阈值，如表1所示；对比原图在5种算法的运行时间，如表 2所示. 为说明本文算法在处理受噪声污染严重的图像时的优势，以添加密度为0.02的椒盐噪声的5个图为测试图片，如图7(a)所示，对比在5种算法下的分割效果图，如图7(b)～(f)所示.

图6 各算法分割效果图Fig.6 Segmentation results of various algorithm

表1 各算法阈值对比Tab.1 Comparison of the threshold with different algorithms

表2 各算法运行时间对比Tab.2 Comparison of running time with different algorithms s

由图6和图7可以看出，当测试图像为不受噪声影响的原图时，5种方法分割效果相差不大；当图像受噪声干扰严重时，由于文献[5，10-11，14]都未对噪声进行处理，所以分割效果较差，而本文算法由于对噪声点进行了处理，所以有较好的分割效果.

传统二维熵算法及其改进算法的运行时间都包括两部分，即求解二维概率分布过程以及用熵理论求解最佳阈值过程.文献[5]中的传统二维 Renyi熵算法未进行任何优化，故而运行时间较长；文献[10]在用 Tsallis熵进行阈值计算时，为降低运算时间，将求解空间局限在二维直方图对角线上，故算法运行时间有所降低；文献[11]采用灰度-局部方差二维直方图进行阈值求解，局部方差被映射为 64级，解空间大小为 256×64，相较于传统算法而言，解空间缩小，所以运行时间也有所降低；文献[14]用像素点的梯度代替邻域灰度均值，相较于传统二维熵算法，解空间并未压缩，反而在求解各像素点梯度的过程中增加了计算量，所以运算时间增加；本文算法没有像传统二维Renyi熵算法那样将像素点映射到直角坐标系中，而是将所有像素点都映射在极坐标系中，去噪后各像素点都集中在 45°极径附近，偏差很小，所以只需要利用极径信息进行图像分割，由此把二维问题转化为一维问题；另外，本文算法不用求解二维概率分布，大大降低运行时间.

算法的空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度，包括算法本身所占用的存储空间、算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这 3个部分.其中，算法本身所占用的存储空间和算法本身长度有关；算法的输入输出数据所占用的存储空间和所处理数据大小有关；算法在运行过程中临时占用的存储空间则随着算法的不同而变化.由于本文算法和各对比算法处理的测试图片相同，且算法长度相差不大，所以在对比各算法空间复杂度时，仅讨论各算法在运行过程中临时占用的存储空间.为方便讨论，假设测试图像大小为 L×L.根据各算法的原理可知，在算法输入都为该测试图像时，各算法运行过程中临时占用的存储空间都与该测试图像大小有关，即使文献[11]将解空间压缩，但是在计算灰度-局部方差二维直方图时其临时占用的存储空间仍然和测试图像大小成正比，所以文献[5，10-11，14]以及本文算法的空间复杂度都为 O ( L2).

图7 加噪图像分割效果图Fig.7 Segmentation results of noise images

4 结 语

本文提出的基于极坐标系下二维直方图的图像阈值分割算法相较于基于传统直角坐标系下二维直方图的阈值分割算法而言有很大区别，其本质区别在于该算法将图像像素点的灰度信息和邻域均值信息映射到极坐标系中而非直角坐标系中，其优势在于：极坐标系中的极角参量能很好地对像素点类别进行划分，通过相关处理措施即可达到滤噪的效果，这对受噪声污染较严重的图像来说，处理效果更加明显；且滤噪后的图像像素点分布集中，仅通过极坐标系中的极径参量即可进行阈值分割，属于一维算法，从而避免了传统分割算法及其改进算法都需要进行复杂二维运算的问题，实时性良好.实验证明，本文算法相较于传统基于二维直方图的阈值分割算法及其改进算法，分割性能更加优越.

［1］Vidhya K，Revathi S，Sahaya S，et al. Review on digital image segmentation techniques[J].International Research Journal of Engineering and Technology，2016，3(2)：618-619.

［2］Otsu N. A threshold selection method from gray-level histograms[J].IEEE Transactions on Systems，Man，and Cybernetics，1979，9(1)：62-66.

［3］Pun T. A new method for gray-level picture threshold using the entropy of the histogram[J].Signal Processing，1980，2(3)：223-237.

［4］Khehra B S，Singh A，Pharwaha A P S，et al.Image Segmentation Using Two-Dimensional Renyi Entropy[M]. Singapore：Proceedings of the International Congress on Information and Communication Technology，2016.

［5］Sahoo P K，Arora G. A thresholding method based on two-dimensional Renyi's entropy[J].Pattern Recognition，2004，37(6)：1149-1161.

［6］龚 劬，王菲菲，倪 麟. 基于分解的二维 Renyi 灰度熵的图像阈值分割[J]. 计算机工程与应用，2013，49(1)：181-185.Gong Qu，Wang Feifei，Ni Lin. Decomposition based two-dimensional thresholding for image using Renyi gray entropy[J]. Computer Engineering and Applications，2013，49(1)：181-185(in Chinese).

［7］潘 喆，吴一全. 二维 Renyi熵图像阈值选取快速递推算法[J]. 中国体视学与图像分析，2007，12(2)：93-97.Pan Zhe，Wu Yiquan. Fast recurring algorithms of image thresholding based on two-dimensional Renyi's entropy[J].Chinese Journal of Stereology and Image Analysis，2007，12(2)：93-97(in Chinese).

［8］Yimit A，Hagihara Y，Miyoshi T，et al. Fast method for two-dimensional Renyi's entropy-based thresholding[J].International Journal on Computer Science and Engineering，2012，4(2)：176-183.

［9］Cheng C，Hao X，Liu S. Application of 2D Renyi gray entropy and fuzzy clustering in image segmentation[J].Journal of Geomatics Science and Technology，2014，31(1)：62-66.

［10］EIsayed M A，Abdelkhalek S，Abdelaziz E. Study of efficient technique based on 2D Tsallis entropy for image thresholding[J].International Journal on Computer Science and Engineering，2011，3(9)：3125-3138.

［11］Zheng X，Ye H，Tang Y. Image bi-level thresholding based on gray level-local variance histogram[J].Entropy，2017，19(5)：191-1-191-8.

［12］Zhang X M，Xue Z A，Zheng Y B. Fast and precise two-dimensional Renyi entropy image thresholding[J].Pattern Recognition and Artificial Intelligence，2012，25(3)：411-418.

［13］雷 博. 二维直线型 Renyi 熵阈值分割方法[J]. 西安邮电学院学报，2010，15(3)：19-22.Lei Bo. Two-dimensional thresholding method based on linear-type Renyi entropy[J].Journal of Xi’an University of Posts and Telecommunications，2010，15(3)：19-22(in Chinese).

［14］黄金杰，郭鲁强，逯仁虎，等. 改进的二维 Renyi 熵图像阈值分割[J]. 计算机科学，2010，37(10)：251-253.Huang Jinjie，Guo Luqiang，Lu Renhu，et al. Image threshold segmentation based on improved twodimensional Renyi entropy[J].Computer Science，2010，37(10)：251-253(in Chinese).

［15］Xiao Y，Cao Z，Yuan J. Entropic image thresholding based on GLGM histogram[J].Pattern Recognition Letters，2014，40：47-55.

［16］Gu Xiaoqing，Sun Yuqiang，Hou Zhenjie，et al. Fast robust thresholding method based on two-dimensional Renyi's entropy[J].Computer Science，2012，39(9)：284-288.

［17］Fan S，Yang S，He P，et al. Infrared electric image thresholding using two-dimensional fuzzy Renyi entropy[J].Energy Procedia，2011，12：411-419.