T形管内雾状气液两相流相分离特性研究*

敬加强 尹晓云 Boris N. Mastobaev Anvar R. Valeev 孙杰 刘力华

(1.西南石油大学石油与天然气工程学院 2. 油气消防四川省重点实验室 3. Department of Transport and Storage of Oil and Gas, Ufa State Petroleum Technological University4. 西安交通大学动力工程多相流国家重点实验室 5.中国石油天然气股份有限公司西南油气田分公司通信与信息技术中心)

0 引 言

管汇具有收集流体并同时进行流体分配的双重功能[1]，被广泛应用于油气田生产工艺系统的各个环节。但管汇系统中普遍存在并联引出管内气液两相流量分配不均(偏流)及气液比例不同(相分离)的现象，以及由此引起的油水分离器溢油冒顶或分离紊乱[2]，稠油开采中高温高压水蒸气不能等干度分配[3]，海上平台气液分离器冗余能力设计过大[4]等问题，不仅影响下游生产单元工作效率和运行安全性，而且增加了总投资成本。

管汇系统中并联引出管内两相流动分配不均的原因在于两相流在构成管汇的基本结构T形管内的分布不均。目前，国内外研究者已针对T形管内气液两相组成的分层流[5-7]、波状流[8-10]、弹状流[11-13]及环状流[14-16]等特定常见流型的流动特性、压降规律及相分离特征开展了大量的研究工作，但很少有关于T形管内泡状流[17-18]和雾状流[19]相分离的研究报道。

本文以T形管作为研究对象，应用计算流体力学ANSYSY Fluent软件，结合气液两相流的基本理论，对水平主管内的空气-水雾状两相流工况进行三维数值模拟，分析其在T形管中的流动特征、压降特性及相分离规律，探究造成雾状流相分离的根本原因。研究结果对确保下游设备的安全、经济和可靠运行具有现实意义，并可为实际工程中的管汇设计及优化提供理论依据。

1 物理模型

水平T形管的三维实体模型如图1所示。主管管径0.10 m，长9.00 m，侧支管与水平主管垂直连接，其管径0.08 m，长4.20 m。主管内两相流从左至右流动，流速为25 m/s，混合物在分支处分流，以一定的分流比分别经过直流支管和侧支管流出。为了兼顾计算精度和计算效率，同时考虑到T形管的简单结构，本文采用非结构化四面体网格划分方法对图1所示的模拟计算区域进行网格划分，并使用网格加密技术对管路近壁面的黏性底层内和流动情况较为复杂的分流结构处网格进行局部细化。划分好的网格及其局部放大图如图2所示。

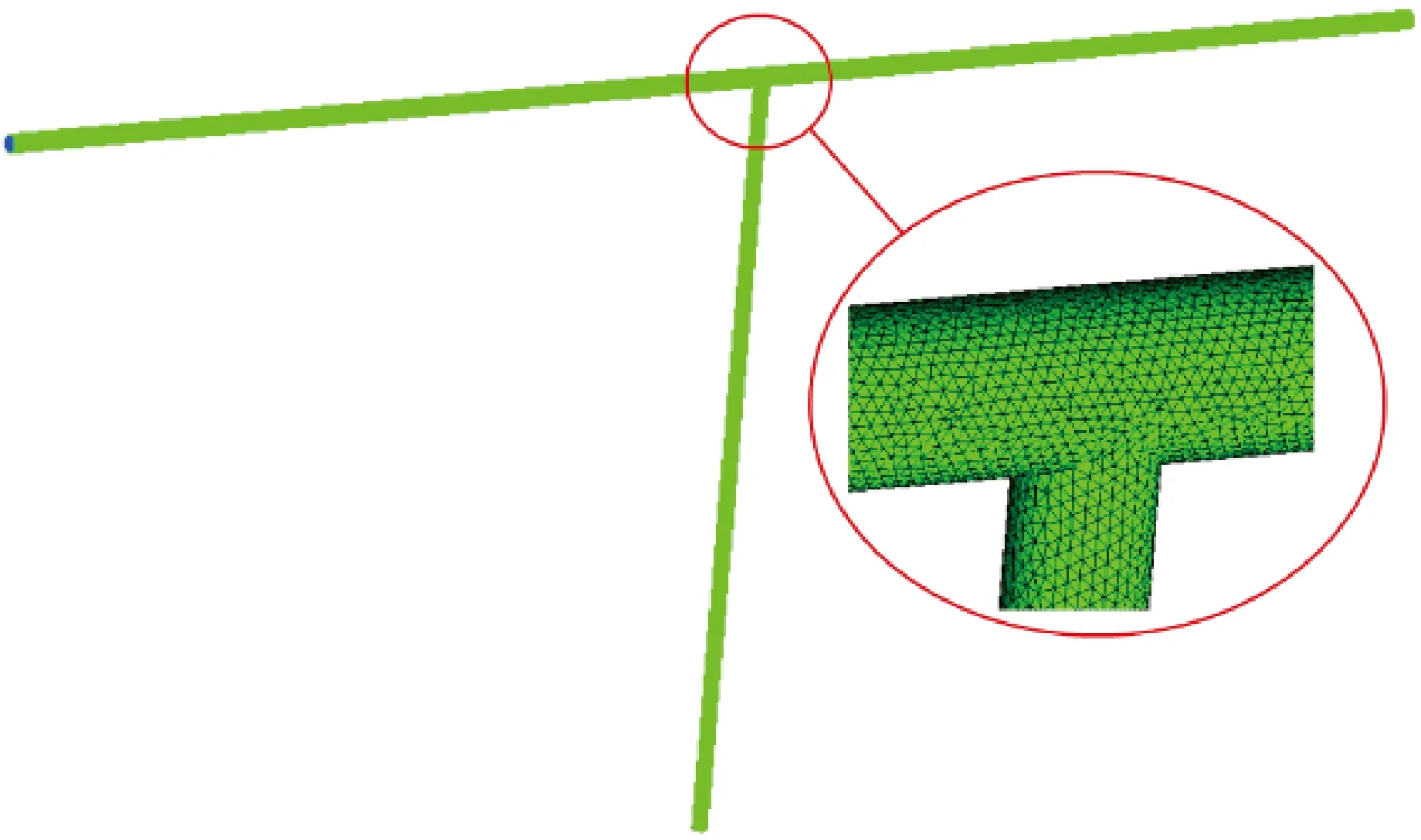
图2 T形管网格划分示意图Fig.2 Schematic diagram for grid division of T-pipe

2 数学模型

由于本文模拟采用含液率较低、液相以液滴状态存在的雾状两相流为基本流型，所以选用Mixture模型求解T形管内气液两相流动过程相关问题。它是欧拉模型的简化，可用于模拟具有不同速度的两相或多相流体或颗粒流，允许有速度滑移和相间穿插[20]。T形管中空气-水雾状两相流动的稳态数值模拟要遵守包括连续性方程、动量方程、能量方程、次相体积分数方程和速度计算方程在内的流体力学控制方程。由于本文所涉及T形管的主管和各支管长度都较短，且计算域内未设有节流装置，可忽略气液两相流在该T形管内流动时的温度变化，故本研究不考虑能量方程。

2.1 基本假设与简化

(1)流体为不可压缩牛顿流体。

(2)T形管内气液两相在饱和温度、压力下保持常物性：空气的密度为1.225 kg/m3，黏度为1.789 4×10-5Pa·s；水的密度为998.2 kg/m3，黏度为100.3×10-5Pa·s。

(3)不考虑重力和浮升力的影响，忽略黏性耗散作用产生的热效应。

2.2 多相流模型

连续性方程为：

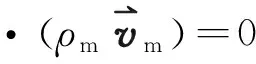
(1)

其中：

(2)

(3)

动量方程为：

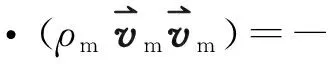
(4)

其中：

(5)

(6)

次相体积分数方程为：

(7)

滑移速度计算方程为：

(8)

漂移速度计算方程为：

(9)

2.3 湍流模型

湍流输运模型包括标准k-ε模型、重整化k-ε模型及可实现k-ε模型3种[21]。本文模拟过程中采用比较成熟且广泛应用的标准k-ε模型，其输运方程如下：

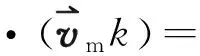
(10)

(11)

(12)

式中：k为湍动能，m2/s2；ε为湍流耗散率，m2/s3；σk、σε分别为湍动能和耗散率对应的普朗特数，σk=1.0、σε=1.3；μ、μt分别为动力黏度与湍动黏度，Pa·s；G为湍动能产生项；C1ε、C2ε和Cμ均为经验常数，其值分别为1.44、1.92和0.09。

3 模型设置及边界条件

3.1 求解模型设置

采用基于压力法的求解器对空气-水雾状两相流在T形管内的流动特性进行稳态模拟。压力速度耦合采用SIMPLE算法，压力方程采用PRESTO模式离散[22-23]，适当调小压力和湍流的松弛因子以促进和保证收敛性。当输运方程中不同变量的残差低于10-5且进、出口管道质量流量相等时，数值计算达到收敛。

3.2 边界条件

以空气-水为工作介质，其在入口处以25 m/s的速度混合后进入水平主管，进口处气相和水相体积分数分别为97.7%和0.3%，液滴粒径为5 μm。出口处为自由出流边界，侧支管和直流支管的分流率均为50%，管壁为无滑移壁面。

4 数值模拟结果分析

4.1 压力场分布

图3为空气-水雾状两相流在T形管中截面的压力分布云图。由图3可知，直流支管内静压整体高于主管，而侧支管静压明显低于主管及直流支管，并且水平主管和各支管在分流后的各管段内压力变化不大，在分流处压力急剧变化。进一步对分流处的压力分布进行分析可知：在直流支管下侧壁面处产生一个高压区，这是因为侧支管的分流作用使直流支管内流量减少，导致此处流速降低而压力产生急剧增大；在侧支管左侧壁面处形成一个负压回流区，这主要是因为局部阻力损失和动压损失的作用，随后流体稳定流出，主要克服沿程摩擦阻力的影响。

图3 T形管中截面压力分布云图Fig.3 Cloud chart for sectional pressure distribution in T-pipe

在分流结构处，两相流体同时受到巨大压差所产生的“吸力”作用[17]，但由于空气和水密度差的存在，两相间的惯性力相差很大，致使气液两相产生了不同的运动结果。密度较小的气相容易发生速度方向的改变，从而更易进入侧支管，而密度较大的液相则能保持原来的速度方向继续向前流动。由此可知，压力分布会间接影响气液两相在T形管内的相分离特性。

4.2 速度场分布

图4为T形管内空气-水雾状两相流在中截面上的速度分析结果。由图4可见，两相流体在水平主管内充分混合发展，流速分布比较均匀且保持稳定流动，流经分流处时，速度发生急剧变化。在直流支管中，一方面受侧支管分流作用影响，其管内流量下降，导致流速急剧减小；另一方面受侧支管入口流体携带和漩涡区“吸力”共同影响，其管内流体自上管壁向下管壁流动，导致下管壁附近区域的流速明显大于上侧管壁处，经过分流处一段时间后，管内流动又逐渐恢复至充分混合发展状态。在侧支管中，受惯性作用影响，在其左侧管壁产生漩涡，导致管内流通截面积缩小，使从漩涡右侧流过的流体流速急剧增大，而左侧流速减小，出现明显的高、低流速区，随着流动的继续发展及漩涡的消失，两相流动逐渐恢复平顺，再次达到稳定流动状态。

图4 T形管中截面速度分析结果Fig.4 Sectional velocity analysis result of T-pipe

4.3 气液相分布

空气-水雾状两相流在T形管中截面的气相和液相体积分数分布云图如图5所示。

由图5可知，气液两相在主管内整体混合均匀，而在分流处受流体分流扰动影响出现明显的气液分布不均现象，并且在此范围内，侧支管中气相和液相分布不均现象较直流支管中更为明显。由图5a可见，气相大部分分布在侧支管左侧漩涡区中。由图5b可见，液相主要占据侧支管右侧和直流支管下侧的壁面区域。这主要是因为气相密度较小，惯性力较小，容易发生速度方向的改变从而更易进入侧支管，并且受“吸力”作用更大，而液相密度较大，惯性力较大，流动方向不易改变，但仍有少量液滴受气相携带作用进入侧支管的漩涡区中。在分流处经过一段时间后，各支管内气液两相又逐渐趋于均匀分布。

图5 T形管中截面气液两相体积分数分布云图Fig.5 Cloud chart for sectional gas-liquid volume fraction distribution in T-pipe

4.4 压降分析

空气-水雾状两相流沿T形管水平主管和侧支管轴向的静压、动压及总压变化曲线分别如图6、图7和图8所示。由图6a可知：水平主管在分流前，沿主管轴线方向的截面静压呈线性衰减趋势，这与正常管输压降规律相符；经过分流处后，由于受侧支管分流作用影响，直流支管内流量减小，致使管内压力先在短距离内急剧上升，然后随着直流支管在轴向的延伸而再次呈线性下降规律。由图6b可知：侧支管内压力先急剧下降，这是由于流体受离心力作用，静压能转化为速度能；随后在较短距离内压力呈上升趋势，这是因为流体流动受阻并在此处堆积，使得部分速度能又重新转化为压力能；最后随着流体流动趋于稳定，静压在管输阻力的作用下呈线性下降规律。

图6 沿主管和侧支管轴向的静压变化曲线Fig.6 Axial static pressure variation curve along main pipe and lateral branch pipe

由图7a可见：水平主管在分流前，沿主管轴线方向的截面动压先逐渐上升后趋于稳定；在分流结构处，主管内流体由于受分流扰动影响，致使动压减小，随后经分流处进入直流支管的两相流体又重新发展至稳定流动状态，其截面动压又逐渐趋于稳定。由图7b可见，在侧支管入口处，流体因受离心力作用，静压能转化为速度能，导致动压升高，随后流体流过涡流区，流动截面积增大，流速降低直至流动稳定，故动压先减小，最后逐渐趋于稳定。

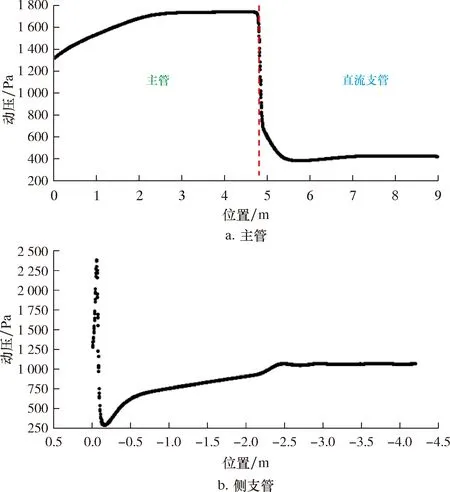
图7 沿主管和侧支管轴向的动压变化曲线Fig.7 Axial dynamic pressure variation curve along main pipe and lateral branch pipe

由于流体的总压取决于静压与动压之和[24]，所以总压曲线的变化规律由静压曲线和动压曲线两者的变化趋势共同决定。从图8可知，主管及各支管内的平滑直线段表示克服沿程阻力所产生的压降，而急剧变化的曲线段表示克服分流结构处的局部阻力所产生的压降。

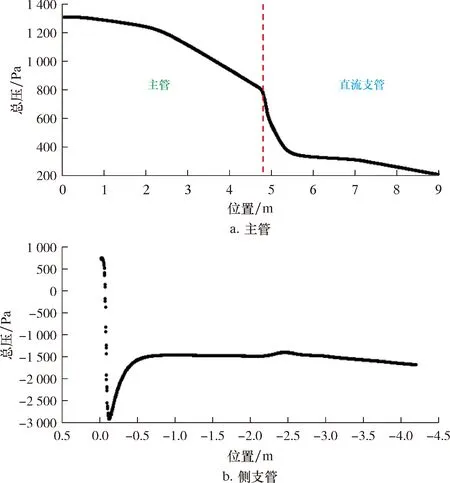
图8 沿主管和侧支管轴向的总压变化曲线Fig.8 Axial total pressure variation curve along main pipe and lateral branch pipe

综合分析T形管中截面的压力、速度及气液相分布云图，并结合水平主管和侧支管轴向的压降变化曲线可知，在不考虑重力影响的条件下，气液两相惯性力差异、两相相互作用及流道结构变化产生的流体扰动是造成雾状两相流在T形管中分配不均的根本原因，且其对相分离的影响程度不同。已有研究表明，气液两相惯性力差异越大，相分配不均现象越明显，而气液两相相互作用越强，相分离趋势明显减弱[19]。由此可知，当流体扰动剧烈，即惯性力起决定作用时，气液相分离程度增强；而当流体扰动微弱，即两相相互作用起主导作用时，气液相分离程度减弱。

5 结论与建议

(1)水平T形管内空气-水雾状流在水平主管分流处的流速与压力急剧变化、相分离现象显著，而在远离分流处，流速保持稳定、压力变化缓慢、气液两相分布均匀。

(2)水平T形管内空气-水雾状流沿水平主管和侧支管轴向的压降(静压、动压及总压)在分流处大幅变化，而在远离分流处，压降变化规律与正常管输压降变化规律一致。

(3)流体扰动、气液两相惯性力差异及其相互作用是雾状两相流在T形管内相分配不均的根本原因。

(4)随着我国海洋混输管网的不断应用和稠油油藏的开发，本文模拟分析能够为低含液率雾状两相流管汇结构设计提供理论依据和指导，可大量节省地面工程运行管理费用，同时对流动安全保障也具有重要作用。但本文仅对某一特定工况雾状两相流在特定结构T形管内的流动过程进行了数值模型研究，在今后的研究中，建议进一步分析不同流动工况和T形管几何结构对雾状两相流相分离的影响，可考虑引入重力和能量方程，并开展对低含液率两相流其他常见流型的研究。