CD70型高压旋塞阀结构强度及启闭特性分析*

李景翠 明祥贵 李亮亮 易先中 贺育贤,4 宋顺平 杨文川

(1. 长江大学机械工程学院 2. 中国石油集团工程技术研究院有限公司 3.中国石油集团渤海钻探工程有限公司工程技术研究院 4.长江大学非常规油气湖北省协同创新中心 5.川庆钻探工程有限公司长庆钻井总公司)

0 引 言

旋塞阀由于具有结构紧凑简单、启闭操作迅速快捷、密封性能好以及安装方便等特点[1]，成为石油矿场固井和压裂作业管汇中最理想的阀门元件。阀体与衬瓦之间为圆柱配合,并通过衬瓦外圆镶入密封件密封。在工作过程中，由于其管道内的流体压力始终处于变化状态，对阀体极易造成破坏，需要对其结构强度及启闭特性进行深入研究。

张智等[2]对油田现场旋塞阀失效现象(泵压由24 MPa减至0，扭矩由3.5 kN减至0，悬重由1 504 kN突降至1 437 kN，泵冲由68 min-1冲增至120 min-1)，提出在旋塞内部台阶处做倒角处理，以减轻应力集中，同时对本体旋塞孔处做加厚处理，增大旋塞阀强度。陈浩等[3]通过现场案例和调研得出方钻杆旋塞阀失效的主要3种形式，即本体强度失效、转动失效和密封失效。陆俊杰等[4]基于微观接触力学，发现当管内流体压力极限为10 MPa，螺钉拧紧圈数为0.05时，旋塞阀密封面疲劳寿命随管内波动流体压力幅值比的增加而增加，增速随管内流体压力幅值比的增加而放缓。奚泉等[5]通过对旋塞阀本体分析，发现应力集中是阀本体失效的一个主要因素，拉伸、内压和扭转载荷对阀本体强度影响依次减小。杨振宁等[6]根据成品油长输管线阀门使用要求(最大工作压力2 MPa，通径200 mm，具有双关断和泄放功能等)，研制了强制密封双关断旋塞阀，并进行了试验和实际应用。沈伟等[7]对核电用软密封旋塞阀(设计压力1.6 MPa)进行了模态分析，并验证了该旋塞阀在正常工况、异常工况、紧急工况和事故工况下均满足ASME设计规范要求。李如学等[8]通过试验发现，采取水冷或油冷的回火冷却方式，可提高顶驱旋塞阀阀体(4330V钢)的低温冲击吸收功。

上述关于旋塞阀的研究多集中在50 MPa压力以下，涉及高压工况下，固井和压裂作业管汇中旋塞阀的强度和流场特征研究还较少。为此，本文针对现行CD70型高压旋塞阀，应用结构力学方法，分析了该阀体在103.5 MPa高压下的工作受力分布情况，并采用CFD方法仿真计算了该阀门在不同开度下的流场特性。研究结果可为CD70型高压旋塞阀的安全运行和操作控制提供参考。

1 旋塞阀有限元力学模型建立

旋塞阀通过旋塞旋转90°，使旋塞上的通口与阀体上的通口相同或分开，实现阀门的开启或关闭，主要由端盖、密封圈、阀体、旋塞、旋塞帽和密封弧片等组成，装配模型如图1所示。考虑到产品实际的复杂性和有限元相关理论，在分析过程中对模型进行简化[9-11]，并做如下计算。

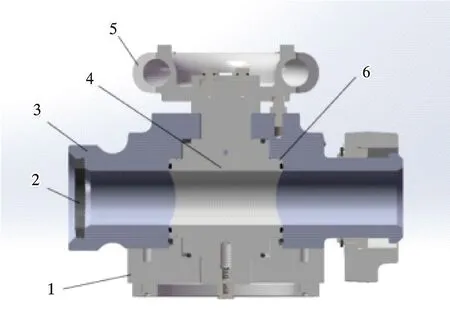
1—端盖；2—密封圈；3—阀体；4—旋塞；5—旋塞帽；6—密封弧片。

中间密封处内表面密封比压q1：

(1)

进口处油壬密封的密封比压q2：

(2)

下端面一个螺栓孔的预紧力F1：

σ0=(0.5～0.7)σs=630 MPa

(3)

F1=σ0A1=222 390 N

(4)

F2=5F1=1 111 950 N

(5)

工作拉力为：

(6)

则右端受压力为：

(7)

式中：p为介质压力，取103.5 MPa；b1为弧片的厚度，取10 mm；b2为油壬密封的厚度,取13.25 mm；m为与流体介质相关的系数，取1.4(气体、高压液体为1.4，水为1)；D1为孔径,取69.8 mm；A1为公称应力截面积,取353 mm2；σs为螺栓材料的屈服极限(与强度等级相关，强度等级取10.9)，查表得σs=900 MPa;S为右端面面积，取28 288 mm2。

2 阀体强度分析及旋转角度与阀门开度研究

2.1 阀体强度分析

为研究阀体进出口相贯处应力与中间过渡圆角关系，基于模型将阀体受力分为5部分，分别对管道内表面施加工作压力103.5 MPa，右端施加压力14.0 MPa，下端面螺栓力施加1 111 950 N，旋塞和阀体部分施加密封比压47.5 MPa，进口处油壬与阀体部分施加密封比压41.2 MPa。左端采用固定约束，在对称面施加对称约束，底部采用径向约束。阀体材料采用42CrMo调质处理，屈服强度930 MPa，弹性模量212 GPa，泊松比0.28，密度7 850 kg/m3。过渡圆角半径取值在0～8 mm，得到过渡圆角半径与总变形量和最大等效应力的关系曲线，如图2所示。总变形量和等效应力云图如图3所示。

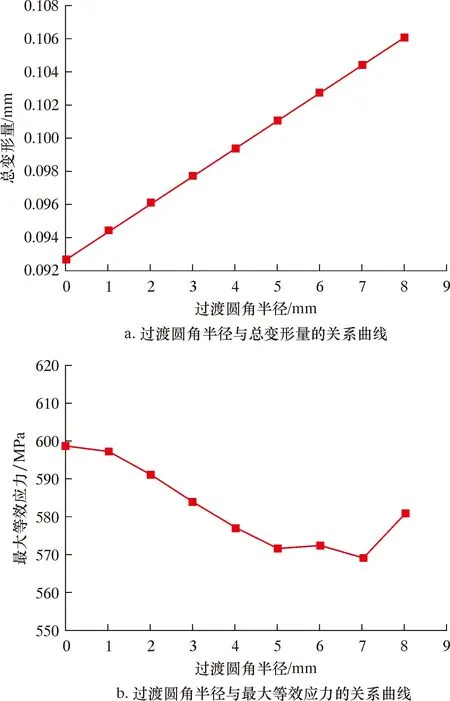
图2 过渡圆角半径与总变形量和最大等效应力的关系曲线Fig.2 Relation curve of transitional round angle radius with total deformation and maximum equivalent stress

从图2可知，阀体总变形量随着中间过渡圆角半径的增加呈线性增加，最大值为0.109 5 mm，但仍处于小变形范围。最大等效应力随着过渡圆角半径的增加先减小后增大，当过渡圆角半径在5～7 mm时，最大等效应力相比于初始时减小最多，最大等效应力出现最小值，约为569 MPa。由图3可知，最大总变形量均出现在阀体出口相贯处，最大等效应力均在阀体进口相贯的下部，最大等效应力为598 MPa，小于材料42CrMo的屈服强度930 MPa，仍然处于弹性变形阶段。

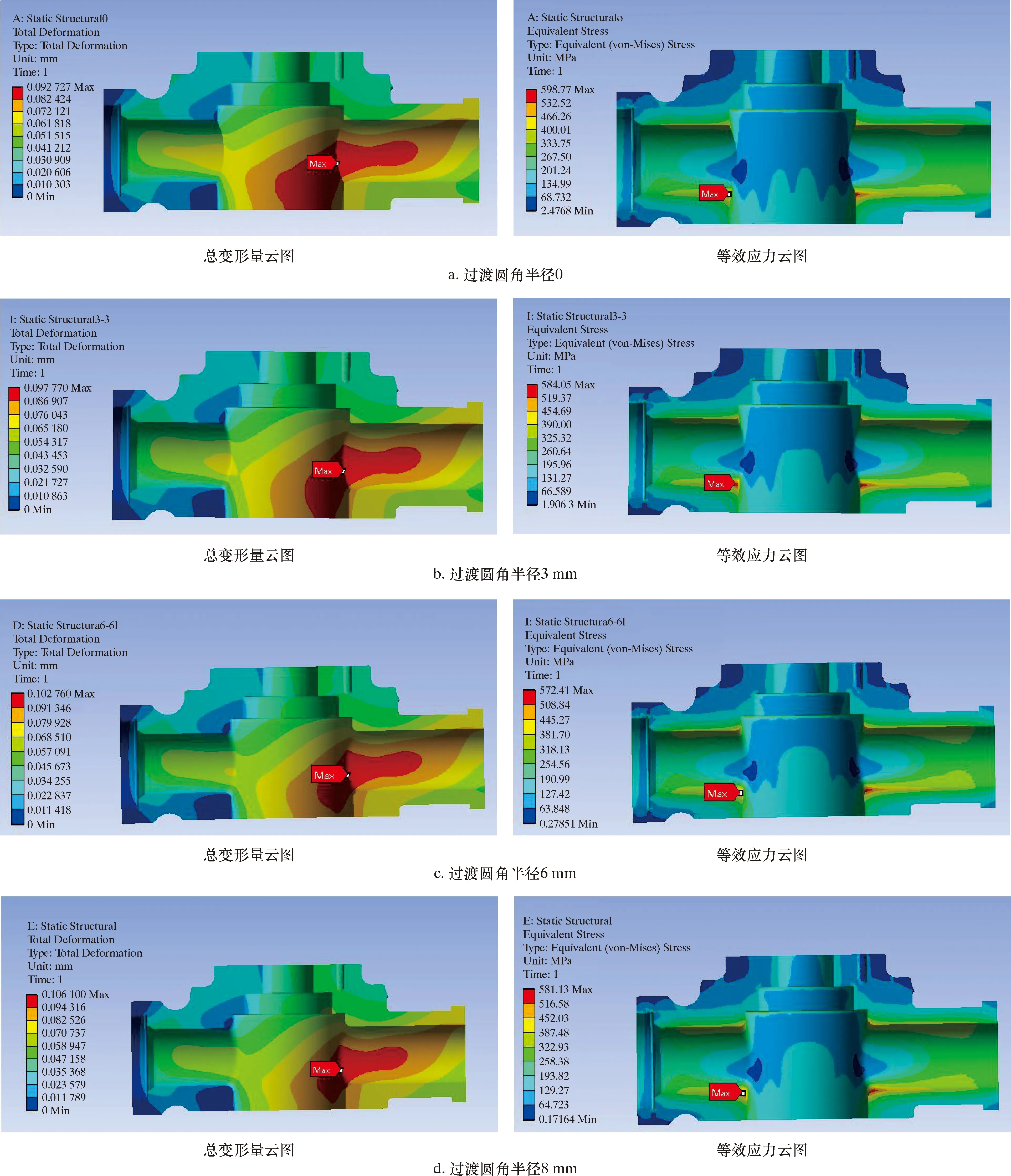
图3 总变形量和等效应力随过渡圆角半径变化云图Fig.3 Variation of total deformation and equivalent stress with transitional round angle radius

2.2 旋转角度与阀门开度研究

旋塞在关闭过程中，由于其过流的面积发生变化，导致阀体内流场也随之发生变化，为此，需要研究旋塞阀开度与旋塞阀旋转角度的关系[12]。本文以旋塞阀旋塞的中心为坐标原点，管道中心流道为y坐标轴，垂直于管道中心流道方向为x坐标轴，建立CD70型高压旋塞阀流道全开和任意开度下结构示意图，如图4所示。其中R1为阀球半径，R1=34.9 mm；R2为阀心流道半径，R2=72.5 mm。通过分析计算，旋塞阀开度与阀的旋转角度关系曲线如图5所示。

由于旋塞阀开启过程中过流面积S与全开时刻过流面积S0的比值即为开度。设旋转角度为θ。

即有开度公式：

(8)

α1=arccos(R1/R2)=61.2°

(9)

α2=π-2α1=57.6°

(10)

由图4可知，开度的求解可以转换为BF与BA的比值。

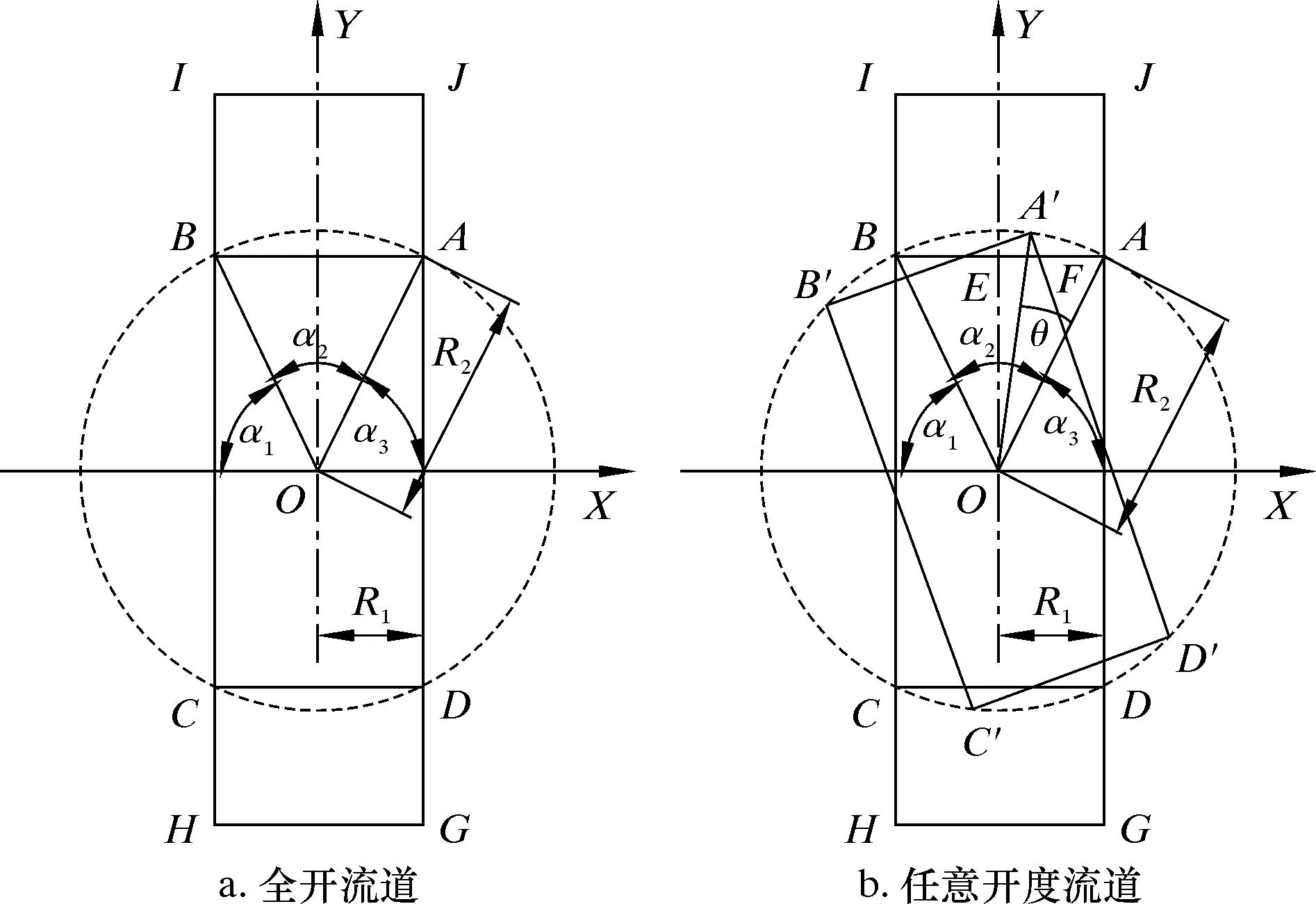
图4 不同开度旋塞流道示意图Fig.4 Schematic diagram for flow channel of cock with different openings

其中，假设A′D′的直线方程为：

y=kx+a

(11)

斜率k的计算式为：

k=-tan(90°-θ)

(12)

A′坐标为A′(R2cos(α3+θ),R2sin(α3+θ))。

则直线A′D′的方程为：

y=-tan(90°-θ)x+R2sin(α3+θ)+
R2cos(α3+θ)tan(90°-θ)

(13)

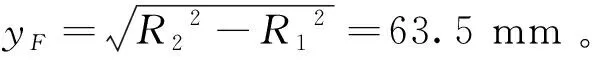
根据上述公式，计算出各旋转角度(5°、10°、15°、20°、25°、30°、35°、40°、45°、50°和55°)分别对应的开度值(92%、85%、78%、70%、63%、55%、48%、40%、30%、20%和7%)。

将以上数据整理后得到如图5所示的曲线。

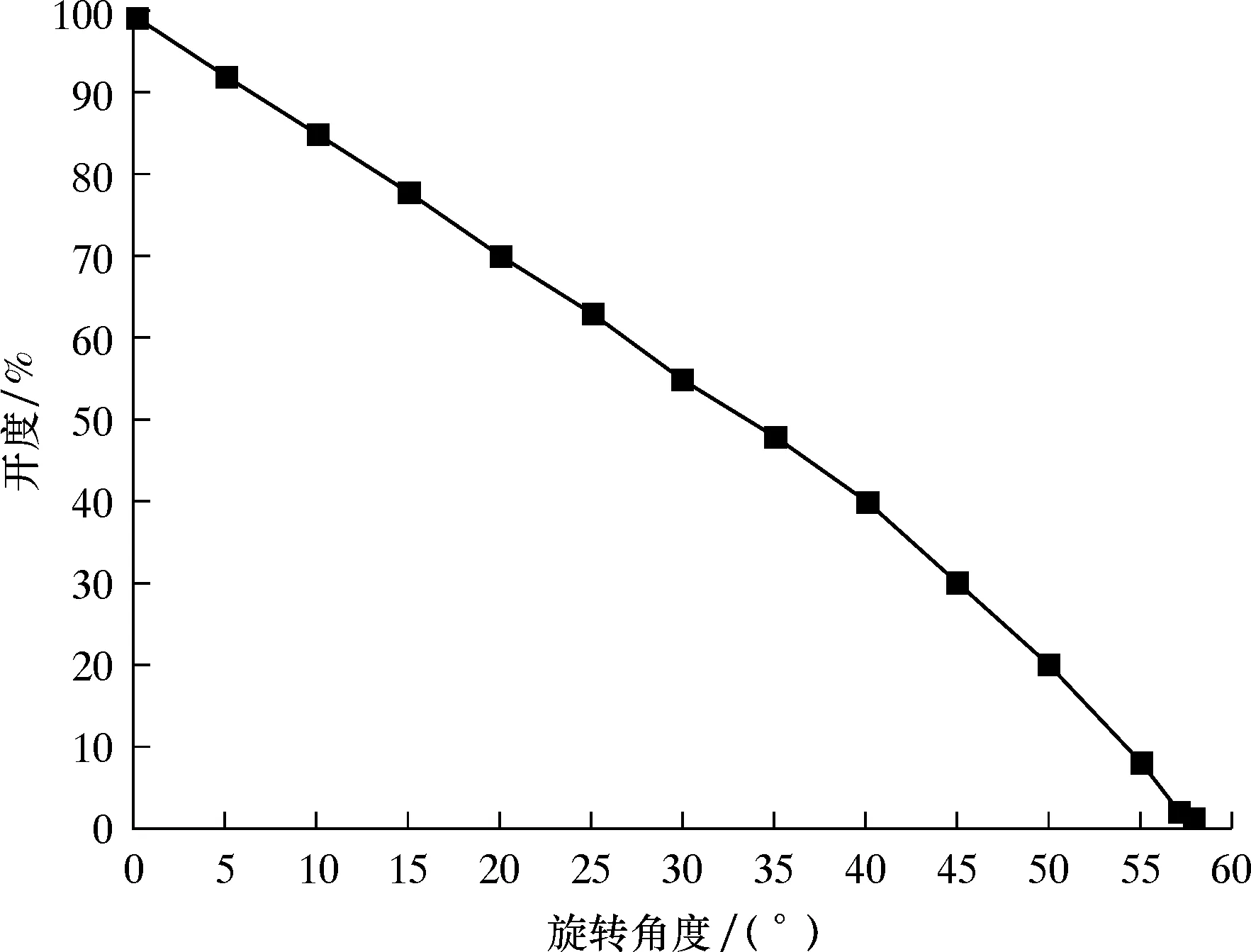
图5 旋塞阀开度与阀旋转角度的关系曲线Fig.5 Relation curve between cock valve opening and valve rotation angle

通过Matlab数值拟合，得到ø69.8 mm旋塞阀开度λ的拟合公式：

λ=-0.000 3θ3+0.014 9θ2-
1.691θ+100.272 6

(14)

3 流场特性分析

在旋塞阀阀门关闭过程中，CD70型高压旋塞阀随着开度不同，阀内部流场存在着变化，为此，需要进行流场分析。分析中，取不可压缩的常温液态水为工作介质，旋转角度依次取5°、15°、25°、35°、45°和55°。

3.1 计算模型与控制方程

考虑到该型旋塞阀工作过程中，通过旋塞的转动实现阀门的启闭，为减少计算量和缩短运算时间，采用二维平面导入分析，求解模型为标准k-ε方程模型。进口边界条件采用速度进口(velocity inlet)，出口边界条件采用自由流出(outflow)，壁面采用Wall 壁面，且无滑移设置。不考虑外界温度对流体黏度的影响，忽略重力对流体流速的影响[13-14]。采用的控制方程[15]如下：

质量守恒方程(拉格朗日法有限体积分析)：

(15)

在惯性坐标系下，动量守恒方程为：

(16)

(17)

能量方程为：

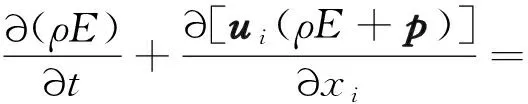
(18)

式中：ρ为密度，kg/m3；t为时间，s；u为流体速度矢量，m/s；ui、uj为u在x、y方向上的分量；Fi为重力体积力和其他体积力，m/s；τij为应力张量，Pa；E为湍流耗散率，m2/s3；keff有效导热系数；Jj’为组分的扩散通量；Sh为化学反应热和其他体积热源项，W/m3。

标准k-ε模型的湍动能k和耗散率ε方程形式为：

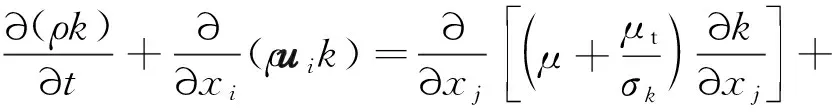
(19)

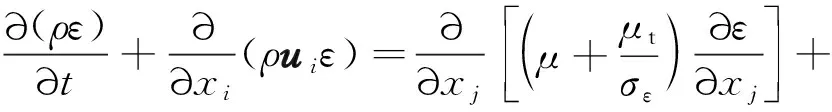
(20)

其中：

(21)

(22)

式中：σk、σε为湍流动能k和湍动耗散率ε的普朗特数，J；μt为湍动能黏度，Pa·s；Cε1、Cε2、Cε3、Cμ均为常量；Gk为速度产生的湍动能；Gb为浮力产生的湍动能，此处为0；YM为可压流体的波动，此处为0；Sk、Sε为自定义项；在不可压缩流体中，常数取值Cε1=1.44，Cε2=1.92，Cμ=0.09，σk=1.0，σε=1.3[16]。

3.2 不同开度下流场分析

当入口速度取15 m/s时，随着旋转角度的增加，阀门开度减小，得到压力分布云图，如图6所示。速度云图如图7所示。关系曲线如图8所示。

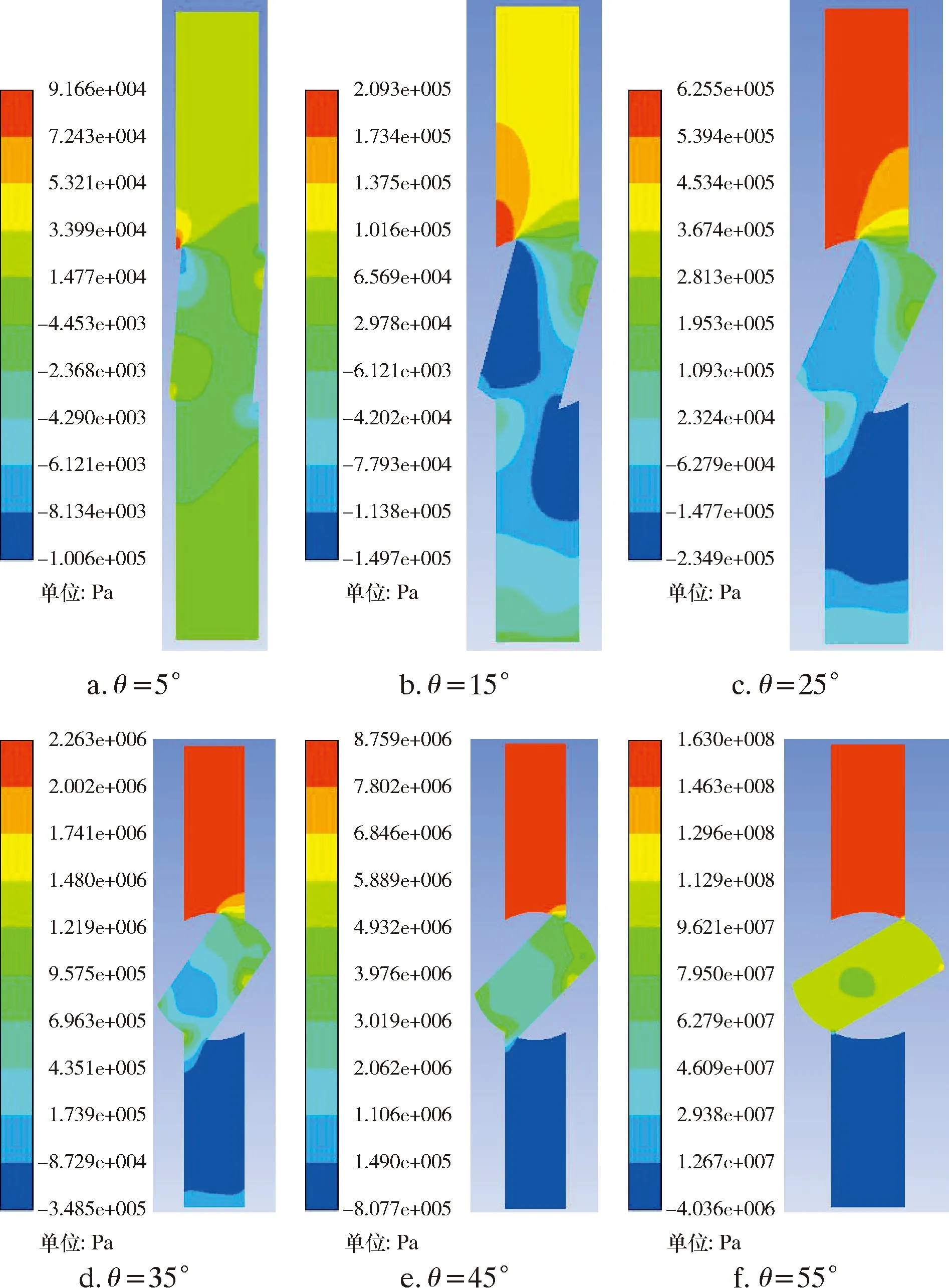
图6 不同旋转角度下的静压分布云图(入口速度15 m/s)Fig.6 Static pressure distribution at different rotation angles (inlet velocity: 15 m/s)

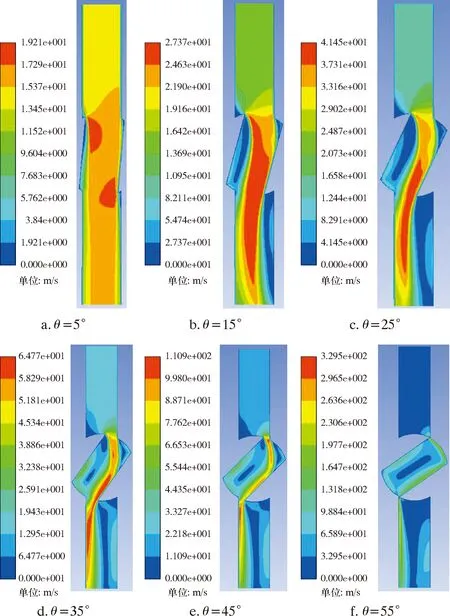
图7 不同旋转角度下的速度云图(入口速度15 m/s)Fig.7 Cloud chart for velocity at different rotation angles (inlet velocity: 15 m/s)

由图6可知：阀前的压力随着旋转角度的增加而增大，阀后的压力随着旋转角度的增加而减小；关闭过程中，阀前形成的高压区和阀后形成的低压区，随着旋转角度的增大相应的范围也增加，压差和压力损失也增加；阀体与中间旋塞接触部分呈现出明显的压力梯度变化。

由图7可知：随着旋转角度的增加，阀前的速度变化较小，但旋塞进口处速度升高；旋塞出口处形成的高流速区域随着开度的减小而逐渐减小，但其最大速度明显升高；旋塞阀在全开时，流体流动状态比较稳定，没有明显的漩涡，当旋转角度超过10°之后，该型旋塞阀阀腔内开始形成回流和漩涡，并且随着关闭角度的增加，旋塞腔内出现方向相反的漩涡，并且越来越大。

由图8可知，在旋塞阀关闭过程中，压差、最大压力和最大速度均随着开度的减小而增加，特别是当旋塞阀开度小于20%之后，压差、最大压力和最大速度显著增加，其中，最大速度从19.21 m/s升高至329.50 m/s，最大压力从0.091 66 MPa

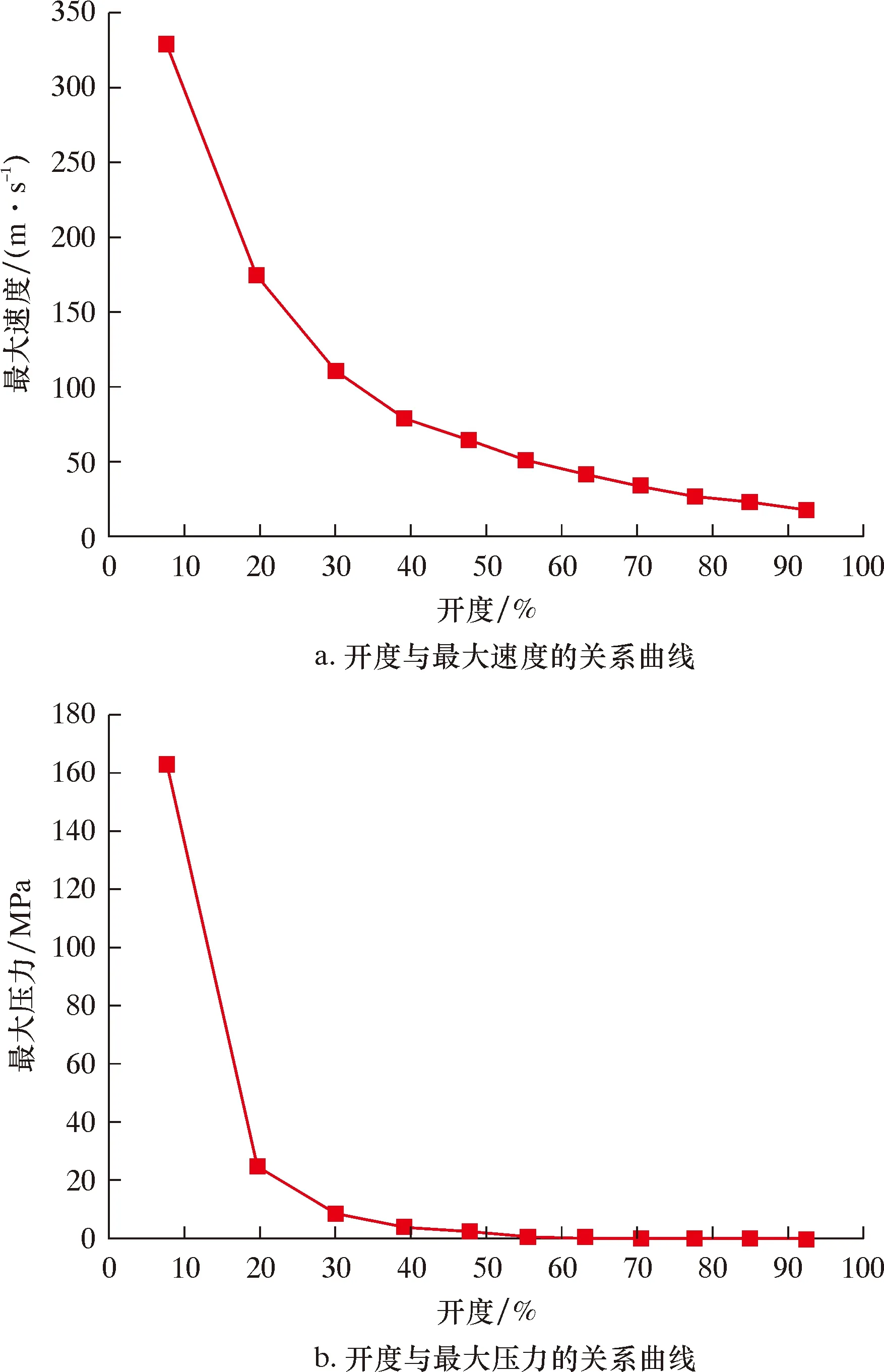
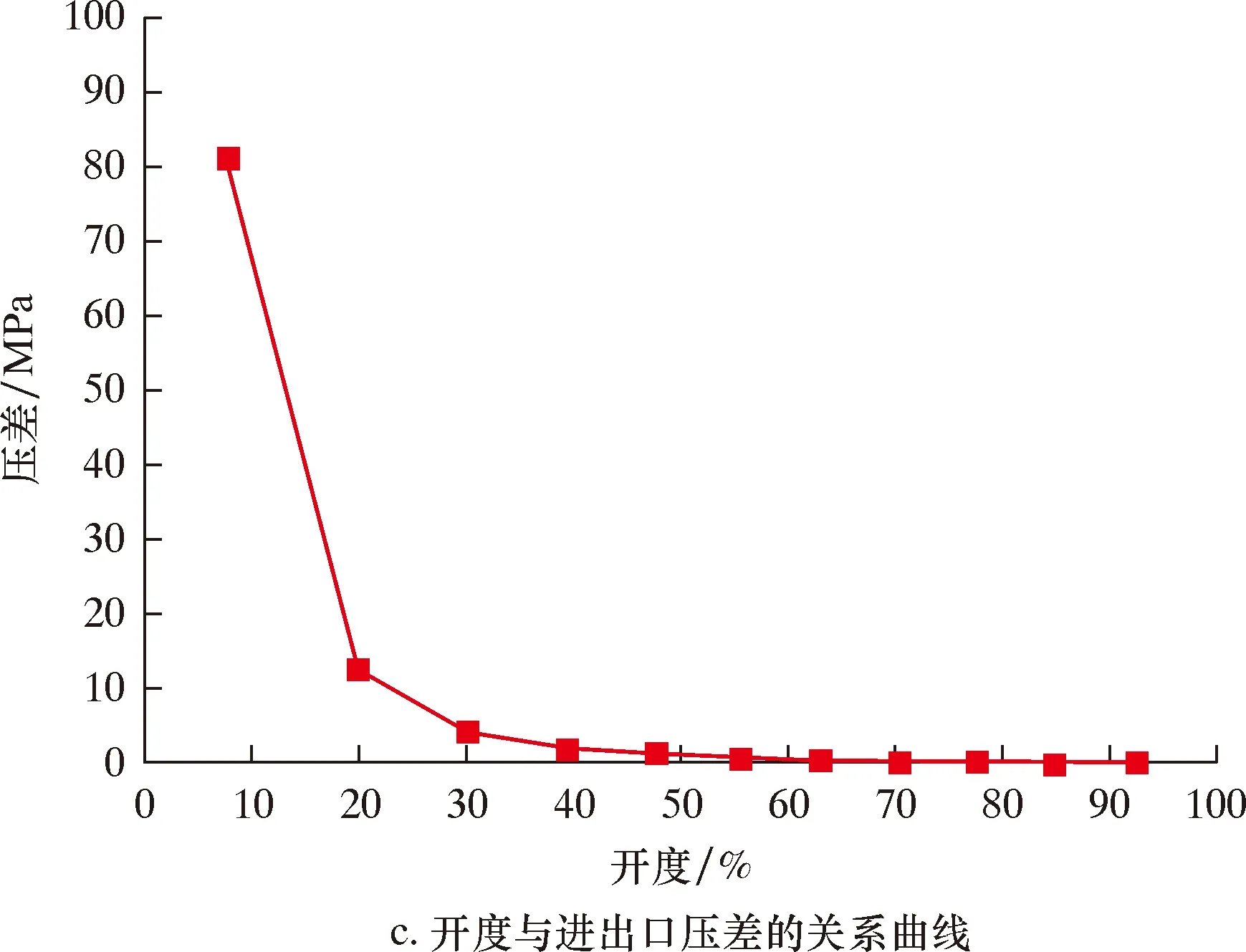
图8 进口速度15 m/s时，开度与最大速度、最大压力和进出口压差的关系曲线Fig.8 Relation curve of opening with maximum velocity, maximum pressure, inlet and outlet pressure difference at inlet velocity of 15 m/s

增大至163 MPa，进出口压差从0.012 MPa增大至81.28 MPa。

4 结论及建议

(1)CD70型旋塞阀的阀体过渡圆角半径从0到8 mm的变化过程中，阀体最大变形量均在出口相贯处，且呈线性增加，最大值为0.109 5 mm。最大等效应力均在入口相贯处下部，最大应力为598.77 MPa，小于材料42CrMo的屈服强度930 MPa。当过渡圆角半径为5～7 mm时，阀体最大等效应力出现最小值，约为569 MPa。因此，建议阀体密封相贯处过渡圆角半径取5～7 mm为宜。

(2)当阀的开度小于20%时，阀前的高压区和阀后的低压区范围增加，阀内开始出现剧烈的回流和漩涡现象，最大速度可达329.5 m/s，最大压力163 MPa；该最大压力已经超出了CD70型旋塞阀的额定设计压力104 MPa，呈现不安全因素。

(3)建议旋塞阀的关断过程要迅速，尽量缩短小开度的工作时间；在旋塞阀启闭控制系统的设计和压裂泵操纵规程的制定中，宜参考可能出现的瞬时涡流速度和最大内压值进行防护性考虑。