钛合金挠性轴裂纹延展规律与寿命预测*

张洪霖 范楷模 王宇鹏 郭添鸣 米凯夫 张一帆

(北京石油机械有限公司)

0 引 言

螺杆钻具是钻井作业中最常用的井下动力工具之一，使用量巨大。随着页岩油气和致密油气等非常规油气资源开发进入提速期，大位移井、超深井和水平井逐渐成为钻井技术发展的主流趋势。工厂化钻井提速和激进钻井参数对于螺杆钻具的输出效能、可靠性以及使用寿命提出了更为严苛的要求，因此，延长螺杆钻具的使用寿命成了必要的研究课题。

万向轴总成是螺杆钻具的主要部件之一，随着结构、材料和工艺的不断优化，各类新型万向轴总成层出不穷。钛合金挠性轴(以下简称挠轴)是近些年出现的较为先进的应用于万向轴总成的材料与结构形式，但由于周期性的行星运动造成的载荷重复加载、井底复杂环境以及钻井介质多样性等因素影响，导致挠轴的失效情况时有发生，使用时长仍旧偏短。为解决上述问题，许多专家学者在结构和材料方面做了相关研究。如练章华和祝效华等[1-2]从优化和改进挠轴结构角度对挠轴进行了研究；王伟等[3]计算了挠轴的疲劳寿命并对其可靠性进行了分析；陈皎和张海威等[4-5]分别对钛合金高周疲劳性能进行了试验研究，但应用于石油工具的挠轴在机械设计方面还有待优化，裂纹延展规律研究还有待加强。鉴于此，本文通过对挠轴设计圆角、造斜弯角和裂纹深度的计算，研究了优选值下挠轴裂纹的延展规律和挠轴的使用寿命，并进行了试验验证。

1 理论推导与钛合金超高周疲劳试验

螺杆钻具钛合金挠轴结构失效的一个常见原因是疲劳，其造成破坏与重复加载相关。疲劳通常分为应力疲劳与应变疲劳，即高周疲劳与低周疲劳。挠轴在钻进时受交变应力作用，且循环次数较高，故应考虑高周疲劳。挠轴呈行星运动，其应力最大与最小水平恒定，应采用恒定振幅载荷[4]。

1.1 公式与理论推导

在弹塑性范围内，利用应力强度因子来描述应力应变场的全部过程，已经形成了许多成熟的理论和模型。其中，Paris模型适用于描述疲劳裂纹的稳态扩展区，稳态扩展区的极大值即为快速扩展区的初始值。因钻井用挠轴的工程属性，不考虑裂纹快速扩展区的残余寿命，即认为挠轴断裂值为稳态扩展区的极大值。由Paris公式[6]有：

(1)

其中：

ΔK=Kmax-Kmin=f(α)Δσπa

(2)

对Paris公式两边取对数，有：

(3)

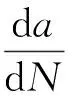
螺杆钻具挠轴裂纹处某点可理解为受恒幅应力Δσ作用，因此Paris公式可以写成：

(4)

可变化为：

(5)

式中：a0为初始裂纹尺寸，m；ac为失稳临界尺寸，m；W为裂纹宽度，m。

由式(5)可知，右端积分为一个常数，令Δσ=ΔS，则有：

ΔSmN=C-1

(6)

m=-logΔSCN

(7)

式中：ΔS为应力幅，m。

公式(6)即为传统的应力疲劳S-N曲线，公式(7)即为钛合金材料常数关系。由推导可知，若疲劳寿命完全由初始裂纹扩展贡献，则S-N曲线等价于da/dN-ΔK关系，也就是说，可以将传统的应力疲劳问题统一到线弹性断裂力学的计算方法之中[6]，同时通过S-N曲线估算Paris公式中的材料常数也是可行的，因此有必要研究该曲线对于疲劳裂纹的延展规律。

1.2 钛合金超高周疲劳试验

本文选用超高周疲劳试验方法，以825 MPa的应力值(钛合金屈服强度)作为疲劳试验预加载应力值的上限，以250 MPa作为疲劳试验预加载应力值的下限，由825 MPa应力开始每隔25 MPa进行一组试验，每组试验有2个试件，规格按有限元计算所得的1阶模态固有频率21.207 kHz的数据尺寸进行加工，如图1所示。利用超声疲劳机(见图2)发生的(20±1) kHz高频机械振动作为试件的激励载荷，使试件产生交变应力场及所需的应变幅值。

图1 试件1阶模态频率Fig.1 First-order modal frequency of test specimen

图2 超声疲劳机Fig.2 Ultrasonic fatigue machine

试验环境为室温，采用压缩空气对试样进行空冷，应力比(试件最小应力与最大应力之比)R=-1.0。试验过程中，通过监测系统监测谐振状态是否改变来判定裂纹是否萌生，若超过1010循环周次，则认为试件不发生断裂，终止试验。

经试验，共计得到48个数值，从而构建得到挠轴主体部分的超高周疲劳试验表。根据疲劳试验表发现，预加载应力由大到小变化过程中循环周次呈不规律增大，在预加载应力为825 MPa时，循环周次为2.52×104和1.71×104，在预加载应力为255 MPa时，循环周次均达到9.99×109以上。根据钛合金超高周疲劳试验表拟合得到挠轴主体部分S-N疲劳曲线及95%可靠度下的应力-寿命范围分布，如图3所示。

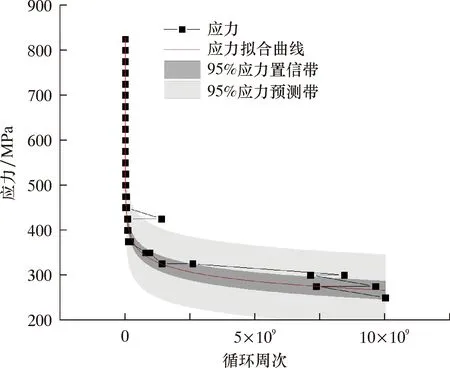
图3 挠轴超高周疲劳S-N曲线图Fig.3 S-N curve of ultra-high cycle fatigue of flexible shaft

由图3可知：随着应力值的下降，循环周次不断增大；应力375 MPa、循环周次108前，挠轴寿命快速下降，离散程度低，后变为缓慢下降，离散程度相应增大。其寿命与应力的关系符合对数分布：

y=a′ln(-b′lnN)

(8)

式中：y为应力，MPa；a′为系数，其取值范围为(-654.065 94±21.296 37)；b′为系数，其取值范围为(-0.028 91±8.107 87×10-4)。

将图3中结果进行优化后，作为有限元疲劳仿真基础数据进行数据导入。

2 有限元计算与分析

设计某种新型172螺杆钻具用挠轴，该挠轴主体部分使用某牌号钛合金材料，两端使用高强度合金材料插接紧固成型。挠轴模型如图4所示。材料力学性能见表1。由于随着挠轴本体直径的增加，挠轴最大应力水平逐渐降低[1]，所以取螺杆钻具内空间可容纳极大值D=65 mm作为挠轴直径。

图4 挠轴模型图Fig.4 Flexible shaft model

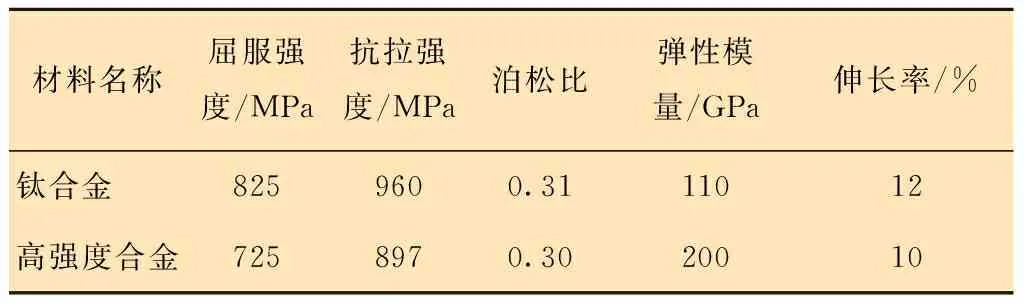
表1 挠轴材料力学性能Table 1 Mechanical properties of flexible shaft materials

在装配好的螺杆钻具中，由于马达总成中心线与传动轴总成中心线不同轴，故有偏心距e的存在，挠轴上端(转子端)受轴向力FY、偏心力FX，挠性扭矩MY和弯矩MZ的作用。将MY和MZ合并，称为扭矩M。挠轴下端(传动轴端)可以简化为固定端[7]。挠轴力学模型如图5所示。

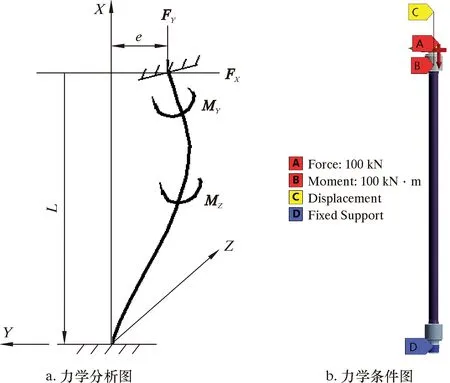
图5 挠轴力学模型图Fig.5 Mechanical model of flexible shaft

挠轴的轴体围绕轴心做行星运动，根据井下受力情况，FY=100 kN，扭矩M=100 kN·m，偏心e用位移表示，在弯角为0°时，e=6.25 mm。

2.1 设计参数取值计算

在行星运动过程中，挠轴圆角半径r过小会造成应力集中，从而降低承载能力；弯角θ过大会造成应力过大，缩短使用寿命，因此本文以该两项参数作为变量，对挠轴进行参数分析，以求得挠轴圆角半径的最佳值和弯角的最大许用值。

以圆角半径r为变量(取值范围为10～250 mm)进行参数化建模，在弯角为0°条件下，应力集中系数表征为：

(9)

式中：σ0表示挠轴本体除应力集中处外的平均应力；σmax表示最大应力，由于挠轴变径处r为最大应力区，所以σmax为变径处的最大应力。

随着圆角半径的不断增大，最大应力与平均应力的比值不断降低，应力集中系数逐渐减小。应力集中系数衰减曲线可大致分为两个阶段，在圆角半径r=50 mm处出现较为明显的斜率分界，在圆角半径r为0～50 mm阶段，应力集中系数衰减较为明显，曲线斜率较大，在圆角半径r为50～200 mm阶段，应力衰减较前阶段小，曲线斜率小，不断趋近于1，如图6所示。

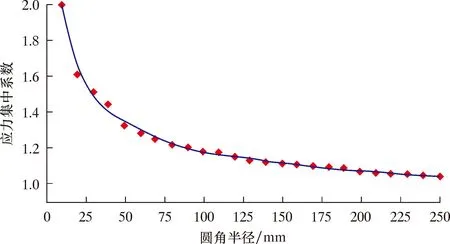
图6 应力集中系数衰减曲线Fig.6 Attenuation curve of stress concentration factor

圆角半径r取25、50、75、100、125、175、200和225 mm，弯角θ取0°、0.50°、0.75°、1.00°、1.25°和1.50°情况下进行有限元计算，结果如图7所示。

图7 不同挠轴弯角下圆角半径与应力的关系曲线Fig.7 Relation curve between round angle radius and stress under different bend angles of flexible shaft

由图7可知：随着弯角θ的不断增大，应力不断增加，呈现非线性特征，θ=0°与θ=0.50°间应力差值最大，最大值出现在r=100 mm处，为250 MPa；随着圆角半径的不断增大，各弯角呈现不同应力特征，θ=0°时，随着圆角半径r的增加，应力缓慢升降，无明显变化；在θ=0.50°、θ=1.50°，应力在r=25～50 mm区间有小幅降低，最大差值达到26.21 MPa，在r=50～100 mm区间应力有上升趋势，最大应力差为109.51 MPa，在r=100～175 mm区间，各弯角下应力均出现不同幅度下降，其中θ=1.25°时应力出现快速下降，最大应力差为71.19 MPa；在r=175～225 mm区间，应力均有不同程度升高，最高应力出现在θ=1.50°、r=200 mm时，值为631.72 MPa，此后各弯角曲线随着圆角半径r增大，应力呈现非相关性，且仍在较高水平。

根据应力值计算，在圆角半径r=50 mm和r=175 mm时，应力出现极值点，两参数除在θ=1.25°外，应力水平基本无差别；在θ=1.25°时应力差为51.96 MPa。综合应力集中系数衰减曲线、钻进造斜时弯角使用情况以及安全系数等因素，优选r=175 mm作为推荐圆角半径取值。

取圆角半径r=175 mm挠轴进行安全系数分析，发现随着弯角的不断增大，挠轴安全系数不断降低，安全系数与弯角θ呈对数分布，如图8所示。由图8可知，在θ=1.50°时，挠轴最小安全系数为1.976 7。安全系数最小值为圆角变径区间，经核算该安全系数值可满足钻井条件下强度安全需求[8-11]。

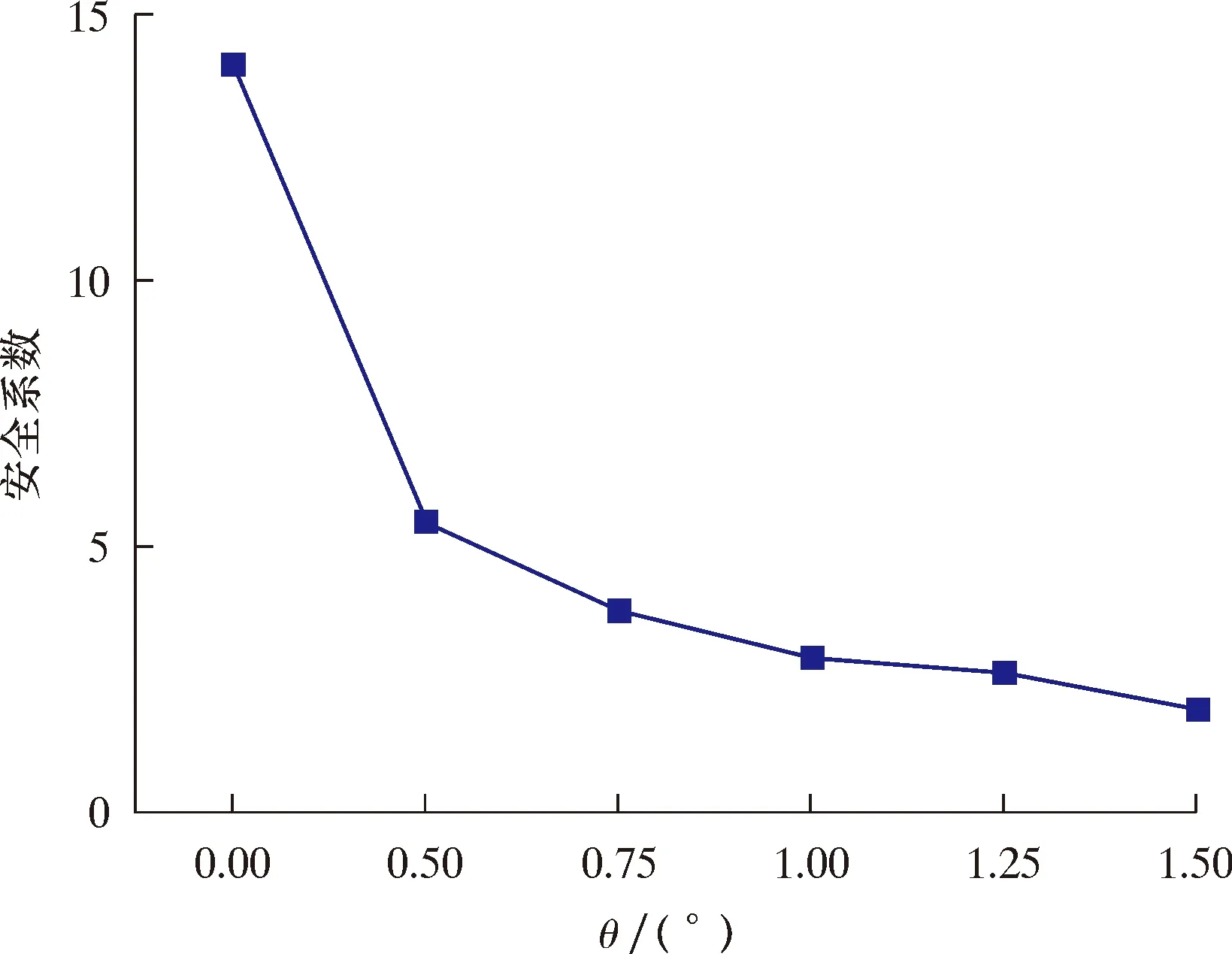
图8 圆角半径为175 mm时安全系数图谱Fig.8 Safety factor map at 175 mm round angle radius

2.2 优选值下的寿命预测

根据有限元计算，挠轴1.50°弯角下圆角半径与循环周次的变化曲线如图9所示。由图9可知，随着圆角半径的变化，循环周次出现波动，在r=50与175 mm处出现极大值，证明了优选值的科学性。以r=175 mm为定值，弯角θ为变量，计算得到应力与循环周次的关系曲线，如图10所示，即等价于优选值下该挠轴的S-N疲劳特性曲线，并得到该挠轴循环周次最小值为1.71×106周次，即该挠轴最短使用时长为1.71×106周次。

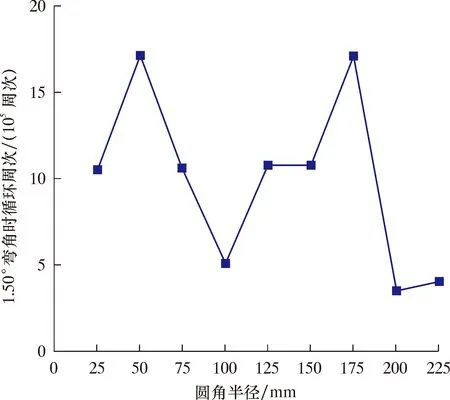
图9 1.50°弯角下圆角半径与循环周次的变化曲线Fig.9 Round angle-cycle times variation at 1.5° bend angle

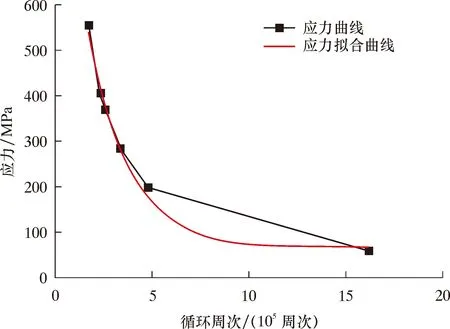
图10 应力与循环周次的关系曲线Fig.10 Relation curve of stress and cycle times

3 裂纹深度分析与裂纹延展规律研究

3.1 裂纹深度分析

选用圆角半径优选值r=175 mm建模，弯角θ为变量，取值区间为0°～1.50°，其余力学条件均不变，将裂纹构建在最易断裂区域，即应力水平最大区域(变径处)，如图11所示。构建裂纹为圆形，表征各向裂纹扩展方向沿主轴方向一致，模拟裂纹由边界裂纹萌生、扩展直至断裂的全周期过程[12-14]。裂纹构建处应力云图如图12所示。

图11 裂纹构建图Fig.11 Crack construction

图12 裂纹构建处应力云图Fig.12 Stress cloud chart at crack construction

经有限元计算，得到各应力计算值，构建裂纹深度与应力的关系曲线，如图13所示。由图13可以看出，随着裂纹深度的增加，应力呈现规律增大，在θ=1.50°时，裂纹深度6 mm处得到最大应力为615.19 MPa，较之前计算的该弯角下的极大值554.62 MPa有一定的增大，表明裂纹萌生前期至稳定扩展期，挠轴仍具有一定抗应变能力，会伴有应力集中现象。裂纹深度到达7 mm时出现瞬断现象，即在应力作用下裂纹深度达到中心距离左右时即会突然断裂。

图13 裂纹深度与应力的关系曲线Fig.13 Relation curve of crack depth and stress

3.2 挠轴寿命极值与延展速率计算

设挠轴疲劳寿命完全由初始裂纹扩展引起，初始裂纹为裂纹初始轮廓最大高度。根据测量，该挠轴裂纹初始轮廓最大高度为3.2 μm，根据上文计算，裂纹深度极限值为7 mm。

不同热处理工艺下，Paris方程中的材料系数C值和m值定量均有差异，拟合方法也会对该值造成影响。本文根据钛合金热处理工艺，参考国内外文献[15-21]进行数理统计，结合公式(7)与有限元计算结果，确定该钛合金材料系数C=9.403×10-11，m=3.607。根据已知条件及计算结果，a0=3.2×10-3mm，ac=7 mm，D=65 mm。在θ=1.50°时，Δσ=49.9 mm。

弯曲作用下，表面圆边裂纹几何形状因子的表达式采用Forman和Shivakumar有限元分析结果[3,20-21]，即有：

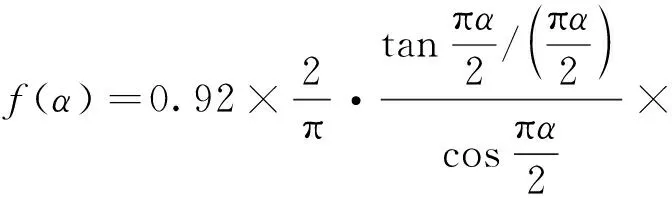
(10)

将上述已知条件代入公式(10)及公式(5)，计算可得挠轴的临界寿命N=2.848×106周次。

设裂纹处应力强度因子最小值为0、裂纹稳定扩展极大值为失稳临界应力强度，根据失稳临界应力强度因子计算公式[6,13]：

(11)

式中：αc=ac/D；KIC临界应力强度因子，MPa·m1/2；E为弹性模量，MPa；r0为挠轴半径，m；δ为自由端挠度，m；L为挠轴长度，m；f(αc)为临界几何尺寸。

代入公式(3)取对数，可得裂纹扩展速率：

(12)

代入已知值计算结果取幂指数后，可得裂纹扩展速率da/dN=1.423×10-5mm/周次。

4 现场试验

按圆角半径优选值r=175 mm加工挠轴后，于川渝长宁区块某井三开使用，钻井深度2 200 m，造斜角度1.5°，钻压100 kN，排量32 L/s。钻进至2 836 m期间由于钻头问题起钻三次后更换旋转导向，挠轴使用时间共计189 h。拆检后发现挠轴变径处出现光亮带，如图14所示。

图14 挠轴实际使用的裂纹萌生示意图Fig.14 Crack initiation in actual flexible shaft

经计算，循环周次约为2.268×106周次，大于计算的1.71×106周次的裂纹萌生时长，但小于2.848×106周次的循环极值，因此判定挠轴应有裂纹萌生。

跨越挠轴表面光亮带沿轴向剖切面进行损伤情况及金相组织检查。在光亮带上可见大部分深度较浅、均匀扩展的裂纹，局部区域较深，其中极值深约2 mm(裂纹扩展方向为周向)，附近存在多条细微裂纹和分叉裂纹，开裂处表面轮廓略有起伏，此外，未见明显表面损伤。浸润后观察发现，裂纹扩展方式为穿晶扩展，裂纹附近组织与其他部位无差异，未见富氧层。光亮带裂纹形貌特征及其附近组织分别如图15和图16所示。由此表明裂纹为周边均匀起源，在2 mm处挠轴仍未断裂，裂纹处于扩展阶段。该金相分析可以对裂纹计算中关于裂纹萌生时间及循环周次的结论进行印证，同时可以证明裂纹萌生期挠轴仍具有一定的抗应变能力。

图15 光亮带裂纹形貌特征Fig.15 Crack morphology characteristics of euphotic zone

图16 光亮带裂纹附近组织Fig.16 Structure near crack of euphotic zone

5 结 论

(1)通过对挠轴圆角应力集中系数分析与有限元计算，确定了圆角半径值的最优解以及弯角许用的最大值。

(2)进行了Paris公式的理论推导与钛合金超高周疲劳试验，确定了最优解下挠轴使用的最短时长。

(3)进行了裂纹深度与应力分析，找出了该钛合金挠轴裂纹深度的最大值；根据有限元计算结果与理论推导结果，计算出了挠轴的极限循环周次为2.848×106周次，裂纹的扩展速率为1.423×10-5mm/周次。

(4)进行了现场试验与金相组织检查，判定了裂纹的起源位置与扩展方式，证明了裂纹萌生及其扩展规律计算的正确性。