基于DPM模型的旋切式PDC钻头流场特性研究*

李劲 边晨阳 刘忠 侯辉辉

(1.中国石油集团工程技术研究院有限公司 2.中国石油大学(北京) 3.中国石油大学(北京)克拉玛依校区)

0 引 言

良好的PDC钻头井底流动特性能够提高排屑效率，减少泥包的产生，从而提高PDC钻头的钻进效率。旋切式PDC钻头是一种新型钻头，具有较宽的流道和旋切刀盘等特殊结构。目前，旋切式PDC钻头存在的主要问题是：水力能量分配不均、涡流区较大、旋切刀盘切削齿附近流速较低以及岩屑不易排出等。在旋切式PDC钻头上采用常规PDC钻头水力结构时井底流动特性并不理想，需要对旋切式PDC钻头的井底流动特性进行研究并对其水力结构进行优化，以提高其水力性能。

众多学者对PDC钻头的井底流动特性进行了研究，况春雨等[1]利用数值模拟方法对牙轮-PDC钻头的井底流场特性进行了研究，发现涡流对排屑效率有较大不利影响。WANG Z.Q.等[2]利用数值模拟方法对双级PDC钻头的井底流场特性进行了研究，发现水力能量分布对涡流区的产生有较大影响。况雨春等[3]认为，在主刀翼的切削齿附近流体流速应较大，因为切削齿表面流速较大时不易发生泥包现象。曹扬等[4]利用数值模拟的方法对旋切式PDC钻头井底流场特性进行了研究，结果发现改变旋切刀盘形状与中心喷嘴曲率后，上返区的流速以及井底流速有所升高，岩屑浓度有所降低。

总结前人的研究成果不难发现：井底涡流区对钻头的排屑效率有严重影响；切削齿附近流速和井底岩屑浓度对泥包的产生有较大影响。曹扬等通过改变旋切刀盘的形状以及中心喷嘴来改善涡流区的状况以及提高井底流场整体流速，但没有解决井底流场水力能量分配不均的问题，同时没有对旋切刀盘附近井底流场进行研究。鉴于此，本文利用数值模拟中离散相颗粒模型(DPM模型)，对旋切式PDC钻头井底流场中的旋切刀盘所在流道的井底流动特性进行研究，对井底流速、井底岩屑浓度和旋切刀盘旋切齿附近流速进行分析，提出2种水力结构改进方案，并对2种改进的水力结构特性进行对比。研究结果可为旋切式PDC钻头水力结构设计提供新的思路。

1 数值模拟控制方程

欧拉-拉格朗日方法[5]是计算多相流的方法之一。其中欧拉法用于计算连续相的运动，拉格朗日法用于计算离散相的运动。在本次数值模拟计算中，钻井液为连续相，岩屑为离散相，且岩屑体积分数小于整体体积分数的10%，满足DPM模型的使用条件[6]。

1.1 连续相控制方程

流体在流动过程中遵守质量守恒定律和动量守恒定律。由于不考虑热传递的问题，所以不涉及能量守恒定律。计算流场采用N-S方程。连续性方程表示为[7]：

(1)

式中：ρ为钻井液密度，kg/m3；t为时间，s；u、v、w表示x、y、z3个方向上的速度矢量。

x、y、z3个方向的动量守恒方程为[8]：

(2)

式中：Fx、Fy、Fz为微元体上的动量交换项，p为压力。

本文PDC钻头井底流场液相采用标准k-ε湍流模型。湍流动能k方程以及湍流动能扩散率ε方程为[9]：

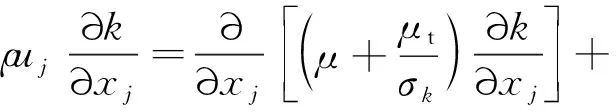
(3)

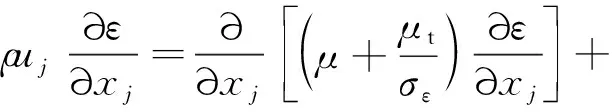
(4)

湍流黏性系数μt=cμpk/ε。式(4)中模型常量取值如下：cμ=0.09，C1=1.45，C2=1.92，σk=1.0，σε=1.3。

1.2 离散相运动控制方程

固相运动通过牛顿第二定律来确定，拉格朗日坐标系下粒子的运动受力方程表示如下[9]：

(5)

(6)

(7)

(8)

式中：up为颗粒速度，m/s；u为流体速度，m/s；gy为重力加速度，m/s2；ρp为颗粒密度，kg/m3；F1为其他方向的作用力，N；Re为相对雷诺数，无量纲；μ为流体动力黏度，Pa·s；dp为颗粒直径，m；CD为拖曵力系数；α1、α2、α3为常数。

1.3 旋转流场模型

钻头在实际工作中旋转钻进，因而本文数值模拟计算时使井底流场围绕钻头中心轴以一定的角速度做旋转运动，流体将受到科里奥利力和离心力的共同作用[10]，计算式如下：

SM,rot=SCor+Scfg

(9)

SCor=-2ρω×U

(10)

Scfg=-ρω×U(ω×r)

(11)

式中：r为位置矢量；U为相对速度矢量；ω为钻头旋转角速度，r/min。

2 井底流场模型建立

2.1 旋切式PDC钻头

本文选用直径216 mm的旋切式PDC钻头，旋切刀盘直径90 mm，采用混合布齿的方法，在旋切刀盘处布置10个锥形齿。旋切式PDC钻头喷嘴编码和切削齿编码如图1所示。

图1 旋切式PDC钻头喷嘴编码和切削齿编码Fig.1 Coding of nozzle and cutter of rotary cutting PDC bit

由于本文主要研究旋切刀盘所在流道的流动特性，故在建立流体计算模型时简化刀翼上切削齿，且将旋切刀盘上的锥形齿简化为圆柱体。旋切式PDC钻头喷嘴按顺时针标号(1号～6号)，切削齿按逆时针标号(1～10)。

2.2 井底流场模型

本文建立的旋切式PDC钻头井底流场几何模型与网格模型如图2所示。井底流场模型包括内流道、喷嘴、外流道和环空区。使用非结构四面体网格对所建立的模型进行网格划分，并对钻头保径部分至井底底部、旋切刀盘、刀翼部分和喷嘴进行局部加密，同时进行网格无关性分析(见表1)。网格尺寸为5和6 mm时，井底流速基本不变，所以取网格总数为1 308 101。

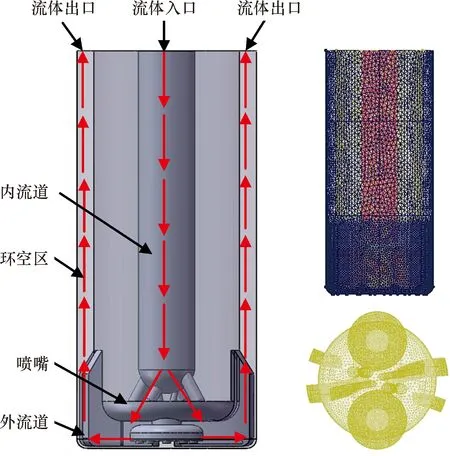
图2 井底流场几何模型与网格模型Fig.2 Geometric model and grid model of bottom hole flow field

表1 网格无关性分析Table 1 Grid independence analysis

2.3 边界条件

模拟时液相为连续相，粒子为离散相，采用标准k-ε模型和标准壁面模型。钻井液为连续相，密度为1 200 kg/m3。入口边界为速度入口，速度为5 m/s，方向为垂直入口面且向内流道射入，入口压力设置为30 MPa。出口采用压力出口，压力为30 MPa。井底流体模型按照顺时针方向旋转，转速200 rad/s。在刀翼下半部分和旋切刀盘下的切削齿处设置粒子射入面以模拟实际岩屑的生成，如图3所示。粒子颗粒直径为2 mm，质量流量为1 kg/s，采用惰性颗粒，密度为2 300 kg/m3。DPM边界设置中将进、出口面设置为捕获，其他壁面设置为反弹。

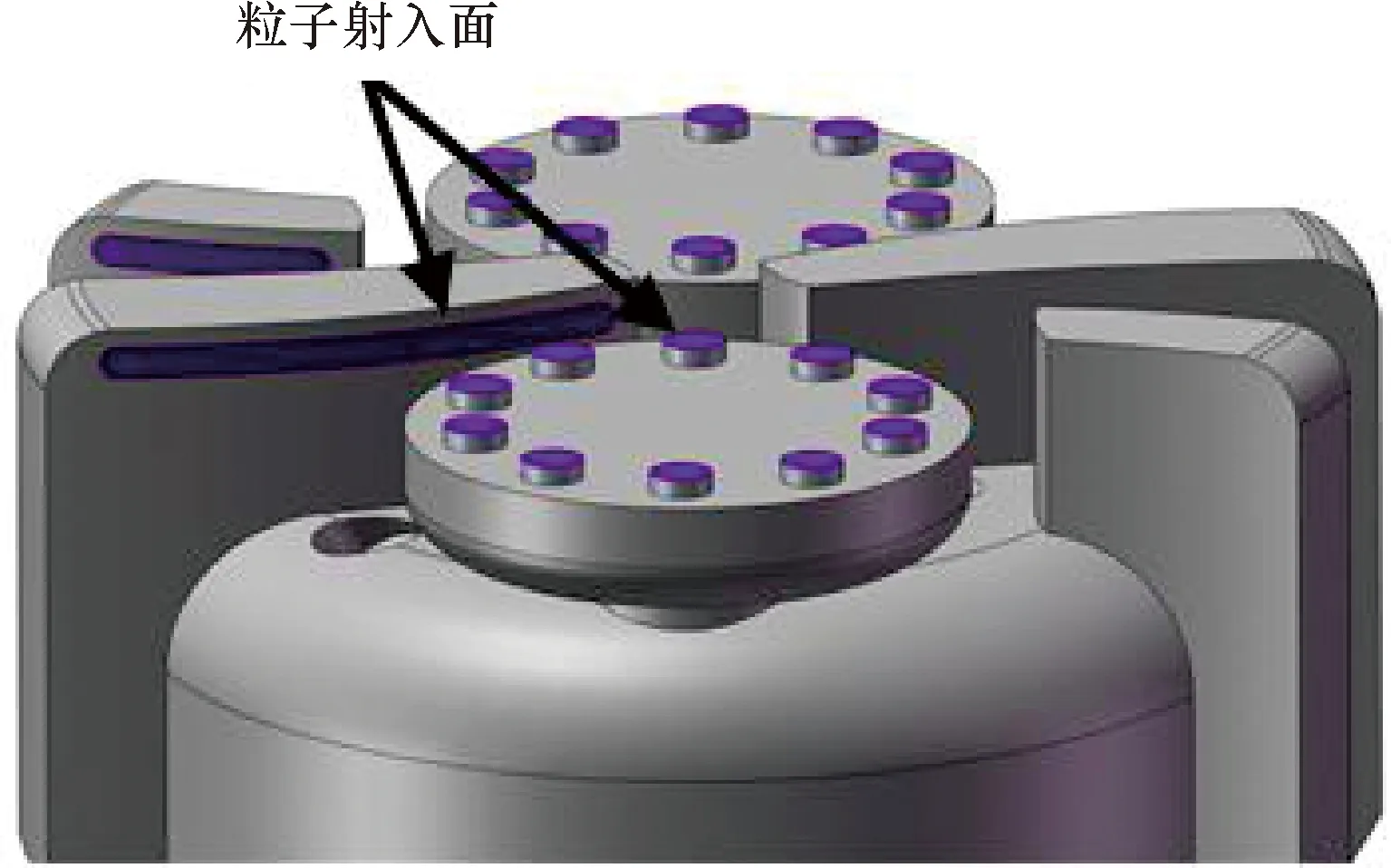
图3 粒子射入面示意图Fig.3 Schematic diagram for particle injection surface

3 旋切式PDC钻头流场特性研究

旋切式PDC钻头井底等流速图如图4所示。从图4可以看出，在两个旋切刀盘中心处水流零流速区较大，切削齿靠近中心一侧流速较低，即旋切刀盘处的水力能量较低，携岩与清洗的效率不高。旋切刀盘处流速较低的可能原因是旋切刀盘所在流道比普通的PDC钻头流道更加宽阔，导致旋切刀盘处没有足够的水力能量用于携岩，岩屑在旋切刀盘处不易排出，甚至产生泥包，进而影响整个钻头的切削效率。

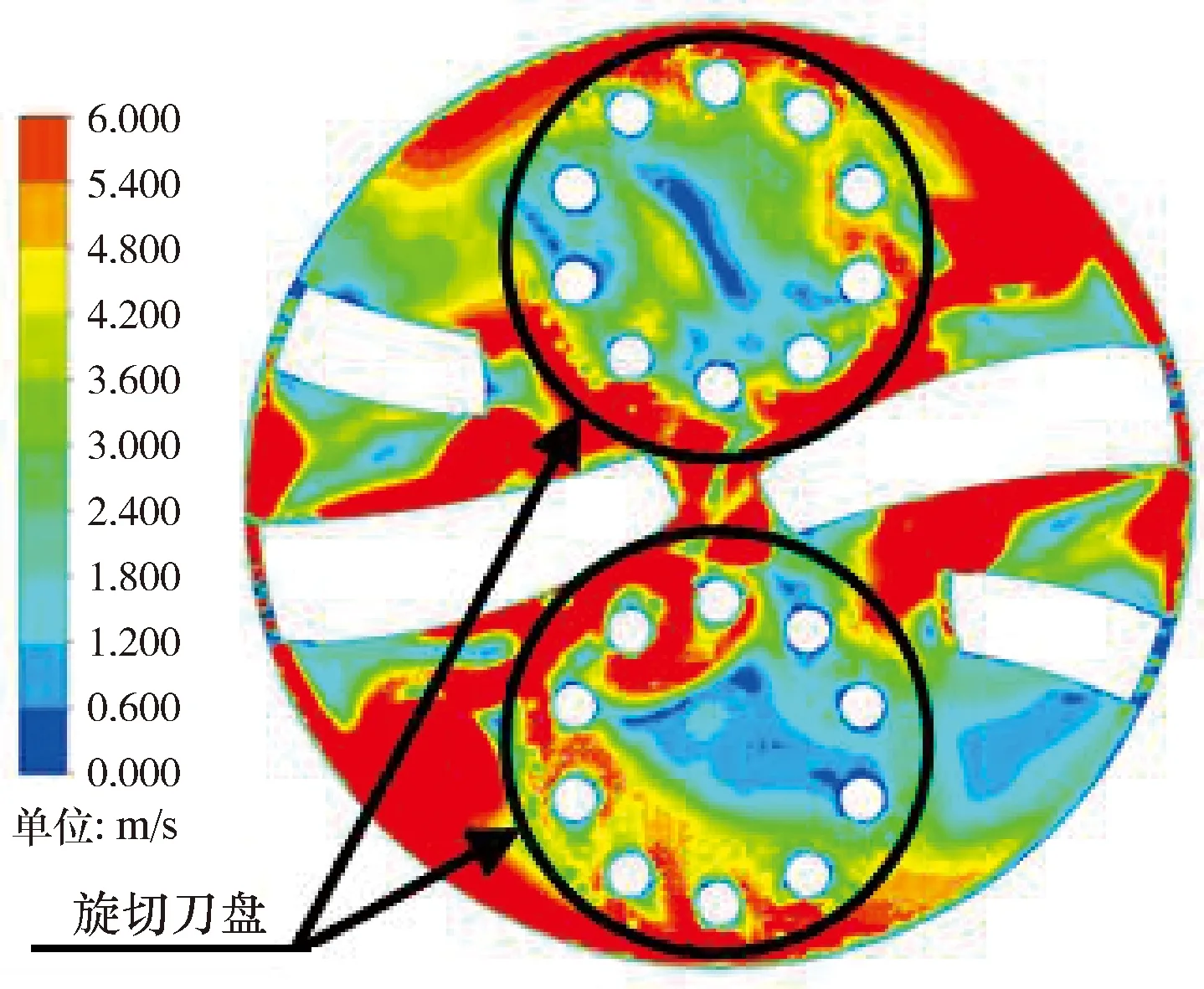
图4 旋切式PDC钻头井底等流速图Fig.4 Bottom hole uniform flow of rotary cutting PDC bit

旋切式PDC钻头井底岩屑颗粒质量浓度云图如图5所示。由图5可知，在钻头中心位置、钻头边缘位置和旋切刀盘边缘位置岩屑质量浓度较高。产生这种现象的原因可能是：井底水力能量分配不均，较宽流道中的岩屑无法被水流高效携带出去，造成岩屑在旋切刀盘底部聚集；不合理的水力结构导致大量岩屑无法由钻井液带入环空区，导致岩屑在钻头边缘堆积。

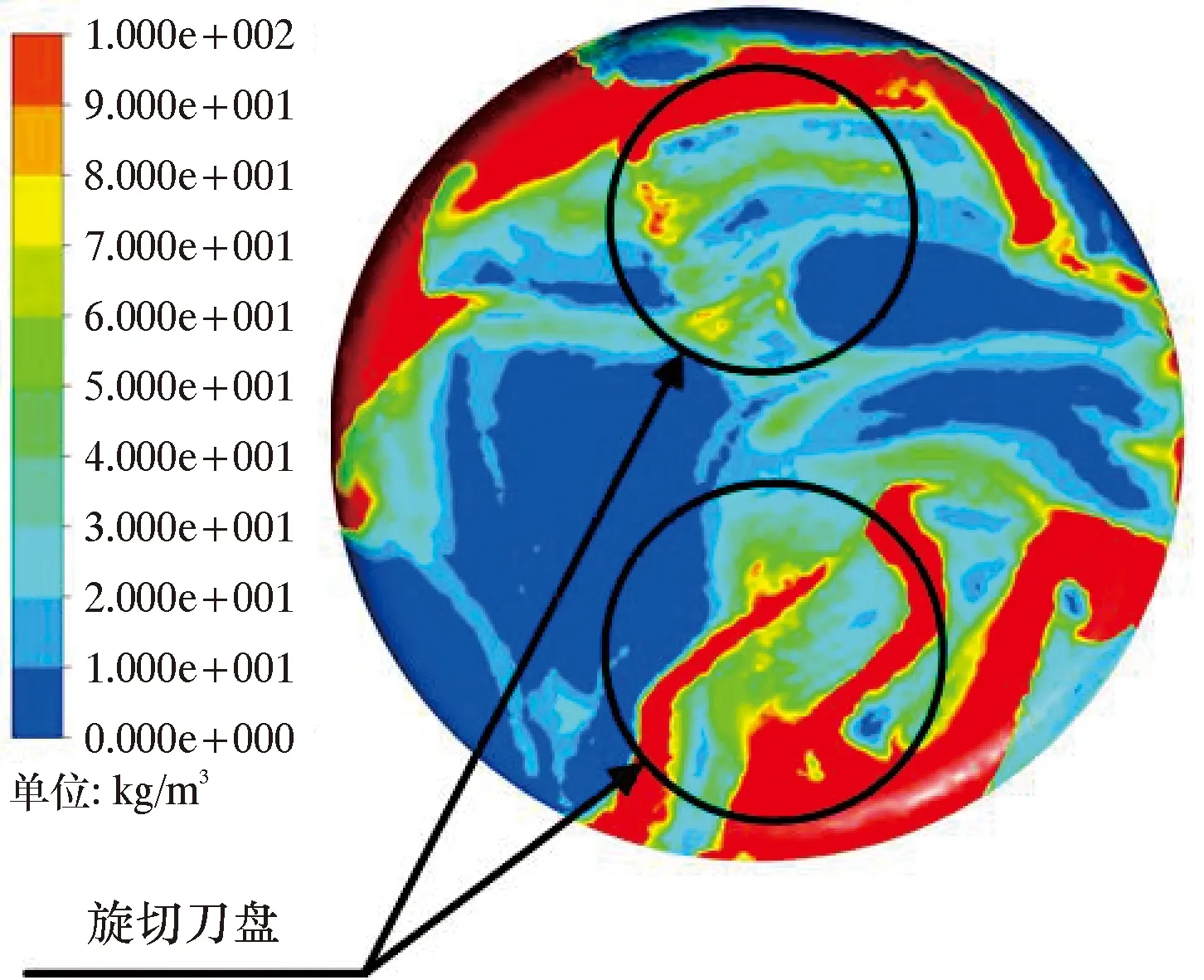
图5 旋切式PDC钻头井底岩屑颗粒质量浓度云图Fig.5 Cloud chart for bottom hole cuttings mass concentration of rotary cutting PDC bit

旋切式PDC钻头井底流线图如图6所示。由图6可知，在两旋切刀盘处和钻头中心处流线轨迹混乱。旋切刀盘处水流迹线混乱可能原因是:2个旋切刀盘相对整个钻头存在转动，阻止水流顺畅地流过旋切盘底，水流在旋切刀盘底部不易流出。旋切刀盘的阻碍导致从中心喷嘴喷出的水流不易排出，在钻头中心产生聚集。同时钻头边缘的1号喷嘴、3号喷嘴、4号喷嘴和6号喷嘴喷出的水流向中心2号喷嘴和5号喷嘴的方向流动，最终导致整个钻头的中心流道轨迹混乱。

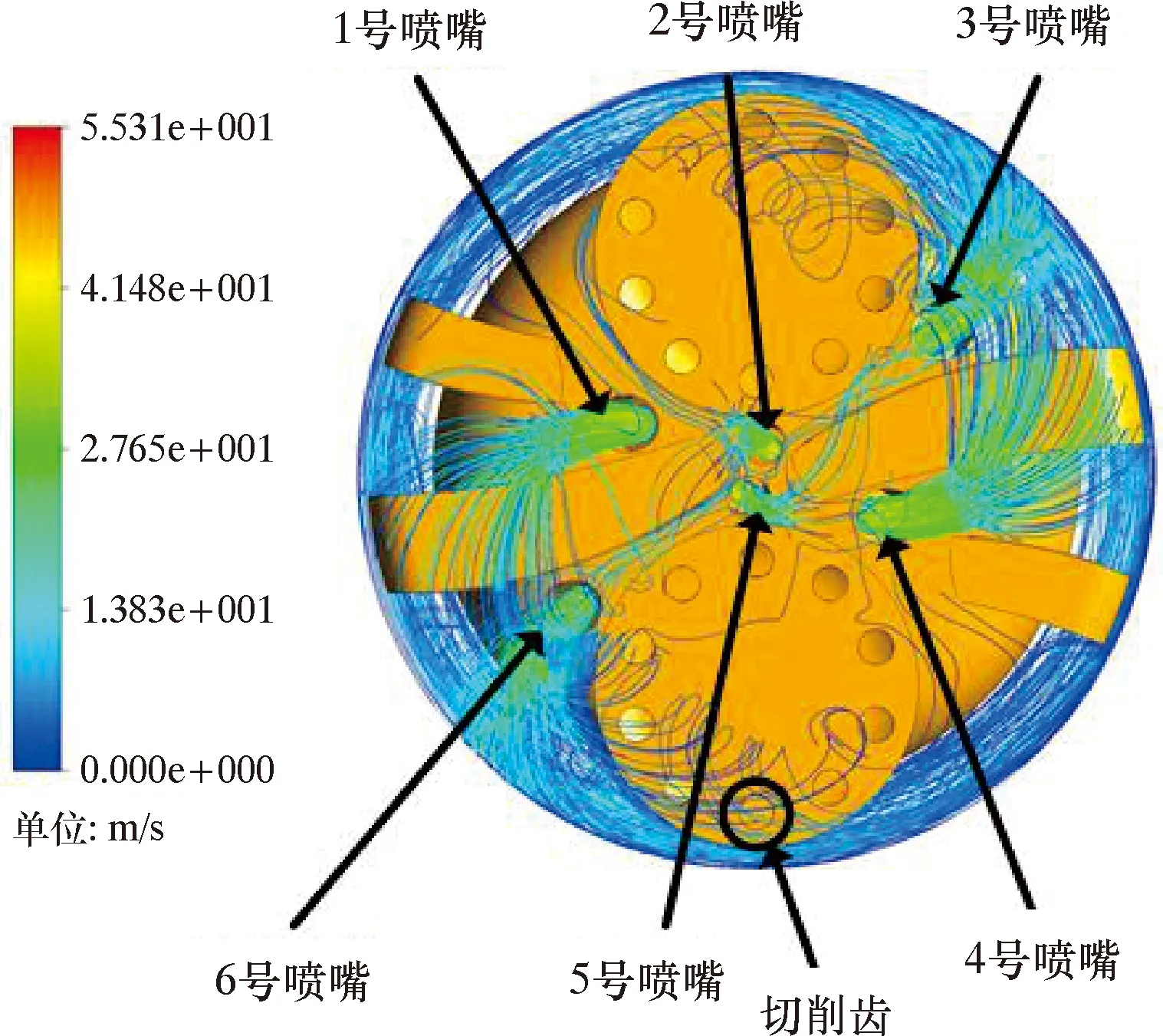
图6 旋切式PDC钻头井底流线图Fig.6 Bottom hole flow diagram of rotary cutting PDC bit

水流迹线混乱表明水流容易在井底形成涡流区，进而导致岩屑排出的时间变长，岩屑容易在井底堆积，甚至形成泥包，从而影响旋切式PDC钻头的切削效率。

旋切式PDC钻头轴向剖面速度矢量图如图7所示。由图7可知，在上返区中的旋切刀盘上部分存在较大的漩涡区。漩涡区产生的原因可能是：水力能量不足，水流在旋切刀盘上产生涡流；旋切刀盘处结构较为复杂，喷嘴喷出的水流在漫流区时被旋切刀盘阻挡向上流动，无法到达旋切刀盘上半部分，在上返区容易形成涡流。

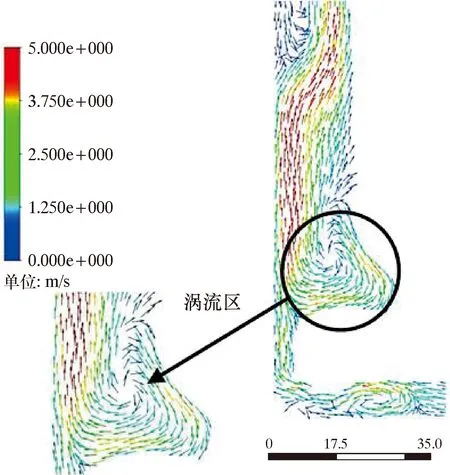
图7 旋切式PDC钻头轴向剖面速度矢量图Fig.7 Velocity vector of axial profile of rotary cutting PDC bit

4 旋切式PDC钻头水力结构设计

针对旋切式PDC钻头存在水力能量分布不均、岩屑容易沉积、水流迹线混乱以及在上返区存在涡流的问题，笔者对旋切式PDC钻头水力结构进行了设计。旋切式PDC钻头流道结构复杂，旋切刀盘的存在会妨碍喷嘴喷射出的水流，所以设计喷嘴时，应该避免水流冲击旋切刀盘上半部分以及水流对旋切刀盘的冲击。基于此原则，设计了在刀翼上偏置安装横喷嘴(偏置式刀翼横喷嘴)和偏置安装斜喷嘴(偏置式刀翼斜喷嘴)2种水力结构。

偏置式刀翼横喷嘴主要利用横喷嘴低压环绕射流速度较快的特点，将岩屑快速带到上返区，可以较好地解决旋切刀盘所在流道流速较慢的问题。同时，由于井底存在水力能量分布不均的问题，需要加大旋切刀盘所在流道的喷嘴面积。增大喷嘴面积能使更多的水流流经旋切刀盘所在流道，使整体流速增大。水流在漫流区的速度随着井底流经距离的增加而减小，故为了提高井底流速，设计斜喷嘴水力结构时应减小喷嘴到上返区之间的距离，同时应加大喷嘴面积改善水力能量分布不均的问题。横喷嘴所在刀翼的安装位置和内部结构如图8所示。斜喷嘴安装位置及内部结构如图9所示。由于旋切刀盘所在流道被旋切刀盘所挡的面积较大，这给大面积喷嘴的布置带来较大的难度，故选择为矩形，两边为半圆形(半圆直径15 mm)的喷嘴结构，如图10所示。

1—内流道底部；2—钻头底部；3—喷嘴流道；4—横喷嘴；5—钻头刀翼。

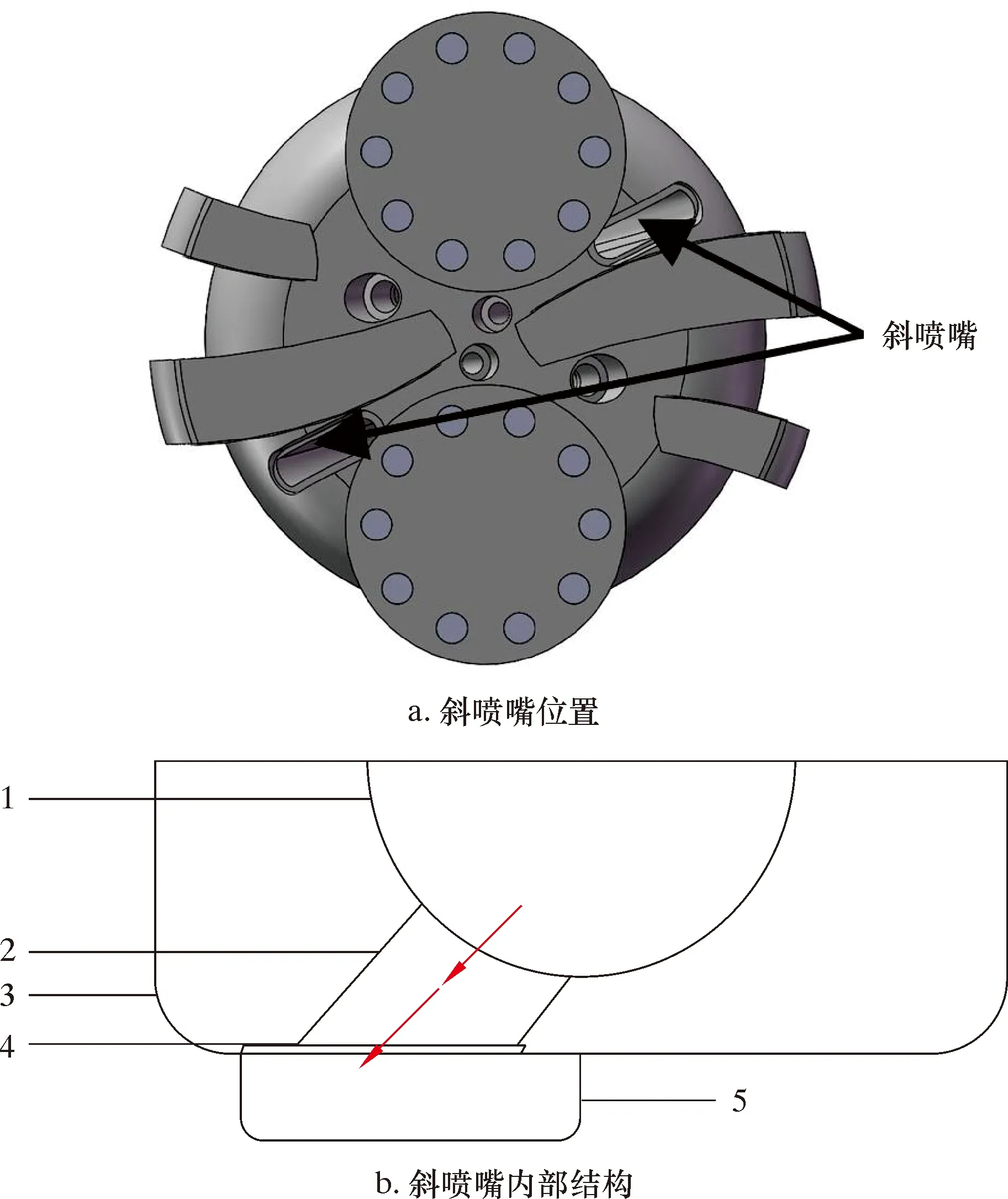
1—内流道底部；2—喷嘴流道；3—钻头底部；4—斜喷嘴；5—刀翼。

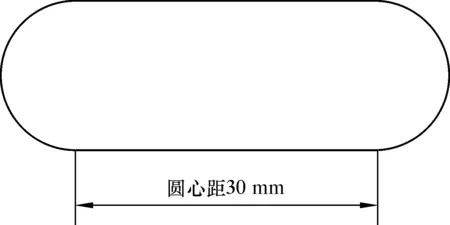
图10 喷嘴形状示意图Fig.10 Schematic diagram for nozzle shape

为了解决旋切刀盘转动造成的流线混乱问题，本文借助水流从喷嘴喷出时的射流附壁效应[11]，使得水流围绕旋切刀盘进行流动，再借助吸卷效应将旋切刀盘处的岩屑带入上返区。在上述设想下，本文对旋切式PDC钻头进行偏置设计，只在刀翼一侧开设喷嘴，使得水流从喷嘴喷出围绕旋切刀盘旋转上升，水流迹线如图11所示。与最初的旋切式PDC钻头水流迹线(见图6)相比，新方案下的井底水流迹线能够围绕旋切刀盘旋转。横喷嘴的旋切钻头水流迹线比斜喷嘴的旋切钻头水流迹线能够更好地覆盖旋切刀盘的切削齿，水流能充分地携岩，从而实现更好的携岩效果。

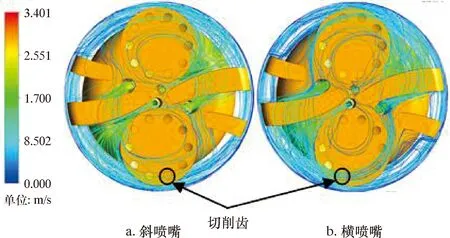
图11 横喷嘴和斜喷嘴的水流迹线图Fig.11 Flow traces of lateral and oblique nozzles

图12为横喷嘴和斜喷嘴旋切式PDC钻头等流速图。与最初旋切式PDC钻头井底等流速图(见图4)相比，旋切刀盘中心处的零流速区明显减小，旋切刀盘切削齿附近的流速更大，并且小流道的水流流经区域更广泛，在旋切刀盘切削齿附近，横喷嘴水流流经区域比斜喷嘴水流流经区域更加充分，尤其是在距离喷嘴较远的8号切削齿位置，横喷嘴作用在切削齿的水流速度要比斜喷嘴作用于切削齿的水流速度更充分，主要是由于射流出的水流流速较快，即使在距离喷嘴较远的切削齿，水流也可以覆盖。小流道水流速度较快，说明横喷嘴结构的大流道和小流道喷嘴分配面积比较合理。

从旋切刀盘切削齿流速变化曲线(见图13)分析，最初旋切式PDC钻头在距离喷嘴较远位置(5号、6号切削齿)的流速较低，流速大约为2.8 m/s，而偏置喷嘴结构由于流体能够围绕旋切盘旋转，大大缩短了5号、6号切削齿与喷嘴的距离，所以在距离喷嘴较远位置的流速为4.0～4.5 m/s，偏置喷嘴结构的5号、6号切削齿附近流速高于传统喷嘴相应位置的流速。旋切刀盘上7号、8号切削齿由于是水流围绕旋切刀盘最后到达的位置，所以7号、8号切削齿附近流速较低，流速为2.5～3.5 m/s，但也与传统喷嘴相应位置的流速大致相等。9号切削齿位置的流速较高主要原因是中心喷嘴水流喷出与原来水流共同作用，在9号位置流速再次增高。斜喷嘴设计方案中，10号切削齿附近流速大约为1.9 m/s，要比横喷嘴和传统喷嘴水流流速都低，原因是10号切削齿在斜喷嘴射流相反的方向。新设计的水力结构比最初设计在旋切刀盘切削齿位置附近的流速都有较大的提高，横喷嘴结构的流速提升更大。

1—7号切削齿；2—8号切削齿；3—9号切削齿；4—10号切削齿。

图13 不同喷嘴的切削齿流速变化曲线Fig.13 Flow rate variation curve of cutter of different nozzles

从横喷嘴和斜喷嘴旋切式PDC钻头井底岩屑颗粒质量浓度云图(见图14)和井底岩屑质量浓度柱状图(见图15)来看，与传统设计下的岩屑质量浓度云图(见图5)相比，两种设计在旋切刀盘底部的井底岩屑质量浓度明显减小。旋切刀盘底部岩屑质量浓度减小的主要原因是：有足够的水力能量作用在较宽的流道；喷嘴改为偏置设计方式，流体围绕旋切刀盘流动上升，从而将旋切刀盘所产生的岩屑带入上返区。虽然旋切式PDC钻头安装斜喷嘴时岩屑质量浓度也可以减小，但效果没有横喷嘴效果好。

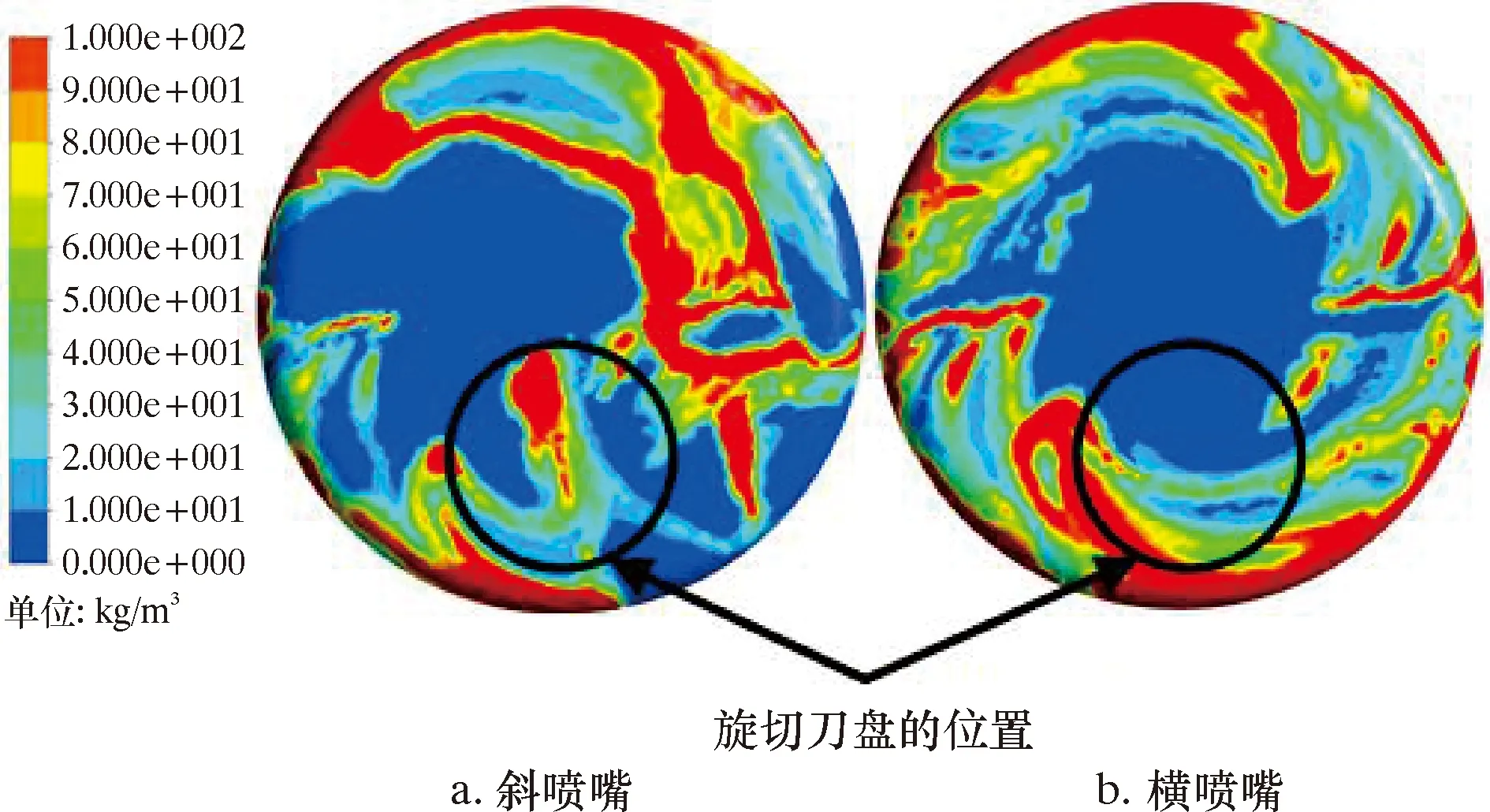
图14 横喷嘴和斜喷嘴井底岩屑质量浓度云图Fig.14 Cloud chart for bottom hole cuttings mass concentration of lateral and oblique nozzles

图15 井底岩屑质量浓度柱状图Fig.15 Histogram of bottom hole cuttings mass concentration

图16为横喷嘴和斜喷嘴剖面速度矢量图。

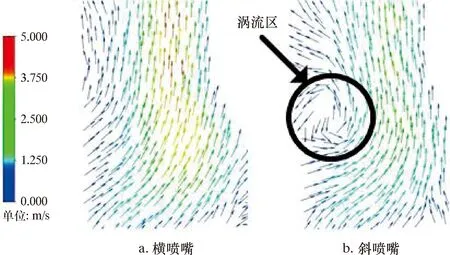
图16 横喷嘴和斜喷嘴剖面速度矢量Fig.16 Velocity vector of profile of lateral and oblique nozzles

由图16可知，采用布置横喷嘴的旋切式PDC钻头在上返区基本没有涡流区，安装斜喷嘴时产生的涡流区基本与最初设计相同，仅仅是位置有所改变。旋切式PDC钻头安装横喷嘴时井底基本没有产生涡流区的原因可能是：从横喷嘴射流出的水流水平速度较大，而垂直于井底方向的水流速度较小，同时由于上返区的压力较小，水流会更加快速地向上返区流动。

通过对井底流线、切削齿流速、井底岩屑质量浓度和涡流区等井底特性研究，发现加大大流道的喷嘴比例面积以及偏置安装横喷嘴的设计更加合理。

5 旋切式PDC钻头横喷嘴优化

为了研究横喷嘴的圆心距对旋切式PDC钻头水力性能的影响，本文设计了不同圆心距(30、40、50、60和70 mm)的横喷嘴，在数值模拟计算时保持喷嘴半圆直径15 mm不变。

图17为不同圆心距的横喷嘴切削齿位置的流速变化曲线。由图17可知：从1号到10号切削齿位置的流速变化趋势基本呈现先上升后下降、又上升；当圆心距为30 mm时，2号切削齿位置的流速7.85 m/s为高峰值；当圆心距为70 mm时，7 号切削齿位置的流速1.21 m/s为最低值。旋切刀盘流速变化呈现这种趋势的主要原因是：2号、3号切削齿位置距离横喷嘴较近，水流从喷嘴流出，首先流经2号、3号切削齿位置。虽然1号切削齿位置距离横喷嘴最近，但是1号切削齿位置并没有处于横喷嘴射流的范围内，所以1号切削齿位置的水流速度较低。4号、5号、6号、7号和8号切削齿位置距离喷嘴越来越远，随着水流围绕旋切刀盘上升，水力能量逐渐减少，没有足够的水力能量用于携岩。

图17 不同圆心距横喷嘴切削齿位置的流速变化曲线Fig.17 Flow rate variation curve of cutter of lateral nozzle with different center distances

9号、10号切削齿位置流速上升的主要原因是：中心喷嘴喷出的水流与从横喷嘴射流出的水流一起流经9号、10号切削齿位置，水力能量得以加强，所以9号、10号切削齿位置的流速再次提升。从图17还可以明显看出，当圆心距为30 mm时，旋切刀盘编码位置整体流速趋势最大，其次是圆心距为50 mm，当圆心距为70 mm时切削齿流速较小。随着横喷嘴的圆心距加大，导致射流流速降低，所以当圆心距为70 mm时，整个井底流速最小。

从不同圆心距横喷嘴井底岩屑质量浓度云图(见图18)来分析，岩屑质量浓度在井壁边缘处较高。随着横喷嘴中心距的增大，井底岩屑质量浓度较高的面积减小，当圆心距为50 mm以上时，井底岩屑质量浓度面积基本保持不变。产生这种现象的主要原因是：横喷嘴中心距较小时，横喷嘴射流速度较高，随着圆心距增大，横喷嘴射流流量增大，但流经的流道面积较小，所以当中心距较小时，井底岩屑质量浓度较高[12]。随横喷嘴圆心距增大，用于携岩的水力能量增大，使水流速度呈现下降趋势，所以流经旋切刀盘的切削齿流速降低，井底岩屑质量浓度有所上升。当圆心距为50 mm时岩屑质量浓度最低。

图18 不同圆心距横喷嘴井底岩屑质量浓度云图Fig.18 Cloud chart for bottom hole cuttings mass concentration of lateral nozzle with different center distances

从不同圆心距横喷嘴的井底岩屑质量浓度柱状图(见图19)来分析，当圆心距为50 mm时，井底岩屑质量浓度最低，为13.03 kg/m3；当圆心距为30时，岩屑质量浓度最高，为35.78 kg/m3。虽然圆心距为30 mm时切削齿流速较快，但是由于喷嘴面积较小，水流流经流道面积较小，流体能够提供的水力能量有限，所以岩屑还是在井底聚集。

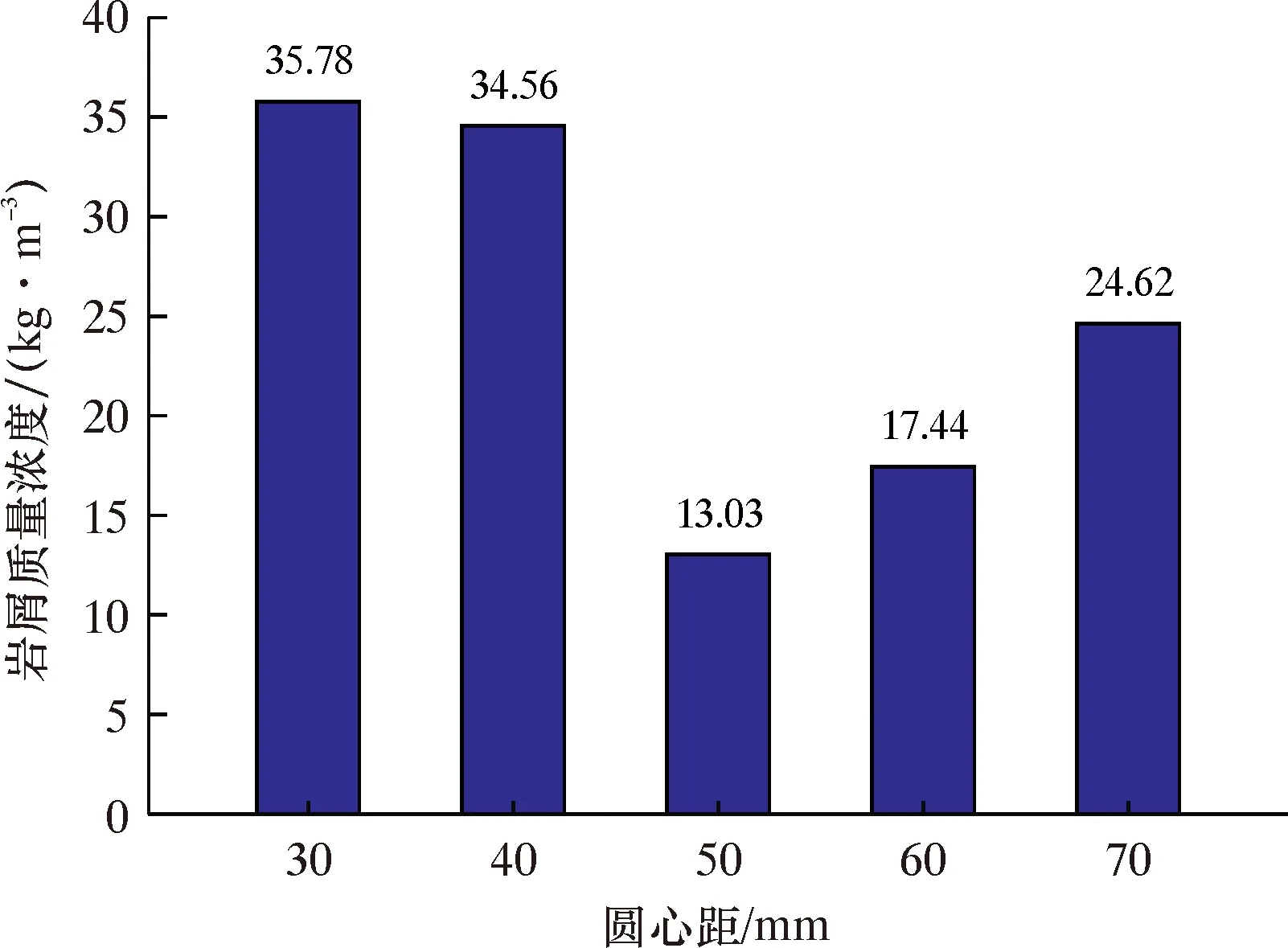
图19 不同圆心距横喷嘴井底岩屑质量浓度柱状图Fig.19 Histogram for bottom hole cuttings mass concentration of lateral nozzle with different center distances

由以上分析可知，当圆心距为50～60 mm时，切削齿附近流速较快，井底岩屑质量浓度较低，所以选用圆心距为50 mm的横喷嘴较为合适。

6 结 论

(1)传统喷嘴的旋切式PDC钻头井底流场存在水力能量分布不均、岩屑容易沉积、水流迹线混乱以及在上返区存在涡流等问题。

(2)采取偏置式刀翼横喷嘴和偏置式刀翼斜喷嘴都能够较好地提高旋切刀盘切削齿附近流速及旋切刀盘中心流速，降低井底岩屑质量浓度，减小涡流区，但偏置式刀翼横喷嘴清洗效果最好。

(3)当偏置式刀翼横喷嘴圆心距为50～60 mm时，旋切刀盘切削齿表面流速最快，井底岩屑质量浓度最小，对旋切刀盘上切削齿清洗效果最好。