连续管可缠绕接头环压关键参数研究*

赵博 邓国辉 茹翔 汪海涛 晁利宁

(1．宝鸡石油钢管有限责任公司 2．国家石油天然气管材工程技术研究中心 3.西部钻探吐哈井下作业公司)

0 引 言

海上钻井平台受场地制约[1]，经常需要将多盘连续管连接使用。陆地钻探也向着超深井方向发展，受滚筒容量等因素的制约，单盘连续管已经不能满足现场施工使用要求，需采用多盘连续管连接一起作业。连续管机械式连接方式可避免场地、人员和设备等因素的制约，成为连续管损坏修复连接或接长的较优选择。连续管管-管机械连接器具有连接强度大于连续管本体强度、安装便捷、检测直观及疲劳性能下降较少等优点，因具有可缠绕性，被称为可缠绕连接器[2]。目前，国外多家油服公司已拥有可缠绕接头及专利，且现场使用效果良好[3-7]。国内中石油江汉机械研究所有限公司已自主研发出适用于外径38.1 mm的连续管速度管柱可缠绕接头，并已成功应用于青海和江苏等油田。

虽然连续管在海上平台及陆地深井有着非常大的需求，应用前景广阔，但油田现场连续管和可缠绕连接器压接参数选择主要依靠人工经验，对环压中关键因素的影响规律研究较少。鉴于此，本文采用ABAQUS有限元模拟软件对连续管环压及拉伸过程进行建模分析，对ø38.1 mm×3.0 mm连续管环压关键参数(环压深度和环压轮半径)进行优选，避免由于环压参数选择不当而引起的连续管失效，同时为现场连续管环压提出指导性意见。

1 有限元分析

1.1 分析对象

可缠绕接头结构如图1所示，主要分为本体部分、接头部分和伸入部分。其中：本体部分要求最大外径与连续管外径相同或略大；接头部分包含预制沟槽和密封槽，采用沟槽设计保证了连接后连续管具有可缠绕性；伸入部分的主要作用为导向或减少应力集中。可缠绕接头与连续管的连接方式为沟槽环压[2]。

1—本体部分；2—接头部分；3—伸入部分。

本模型的建立基于连续管与可缠绕接头环压和拉伸过程，模型包含环压轮、连续管及可缠绕接头。由于连续管环压过程仅涉及可缠绕接头本体部分和伸入部分，故选择接头和伸入部分作为可缠绕接头研究，暂不考虑密封圈。

研究对象为外径38.1 mm、壁厚3.0 mm的CT80连续管，以及外径31.5 mm、环压槽直径6.5 mm、环压槽深度2.3 mm的可缠绕接头。材料力学性能参数如表1所示。

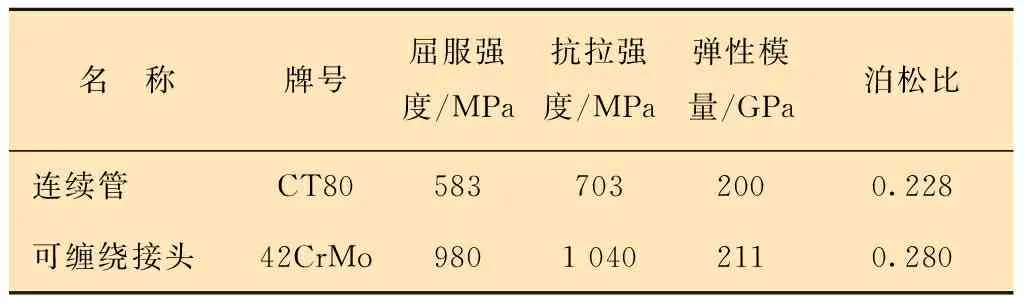
表1 材料力学性能参数Table 1 Mechanical properties of materials

1.2 基本假设

针对环压过程对有限元模型进行简化并做如下假设：①连续管和可缠绕接头均为各向同性材料；②环压轮强度远大于连续管强度，环压轮为解析刚体；③单个环压轮依次环压简化为3个环压轮顺次环压。基于以上假设，连续管可缠绕接头模型可简化为轴对称模型[8-10]。

1.3 网格划分

采用ABAQUS软件，以接头各部件尺寸为基础，采用弹塑性非线性模型进行不均匀网格划分，四边形区域采用CAX4R4进行网格划分(双线性轴对称四面体减缩积分)，三角形区域采用CAX3(线性轴对称)进行网格划分；划分后可缠绕接头单元数为17 757，节点数为18 353，如图2所示。

图2 3.0 mm环压轮压接装配体网格划分Fig.2 Grid division of the crimping assembly of 3.0 mm circumferential crimping roller

由于连续管、可缠绕接头和环压轮皆具有对称性，其中心环向位移为0 mm，连续管轴向拉伸均以分布应力的方式加载在管体端面。

2 弹塑性有限元模型

连续管工作中实际受力状态非常复杂，主要载荷包括边界约束力、环压轮环压压应力、连续管端面拉应力。在有限元分析中，连续管总的载荷列阵F可表示为[11]：

(1)

(2)

(3)

(4)

(5)

连续管总体刚度矩阵K可表示为:

(6)

式中:D为弹性系数矩阵。

连续管总有限元方程为：

Kα=F

(7)

式中：α为连续管综合变形。

通过求解式(7)，得到综合变形α，进而得到单元节点e的位移列向量αe，则变形后的单元应力σ和单元应变ε可通过式(8)和式(9)求出：

ε=Bαe

(8)

σ=D(ε-ε0)+σ0=DBαe-Dε0+σ0

(9)

3 计算结果及分析

3.1 环压深度对压接接头Mises应力的影响

采用环压轮半径4.5 mm，环压深度分别为1.4、2.0和2.6 mm的环压参数对连续管进行环压，对比压接接头最大Mises应力随环压深度的变化规律，结果如图3所示。由图3可以看出，环压深度为1.4 mm时，最大Mises应力位于可缠绕接头最后一个环压凹槽连续管底部；环压深度为2.0 mm时，最大Mises应力位于连续管与可缠绕接头压接位置两侧；环压深度为2.6 mm时，最大Mises应力位于连续管表面。由此得到，不同环压深度，接头最大Mises应力集中位置不同。

图3 半径4.5 mm时环压轮环压最大Mises应力分布Fig.3 Distribution of maximum Mises stress during circumferential crimping with 4.5 mm radius circumferential crimping roller

分析其原因，当环压深度为1.4 mm时，环压轮仅作用于连续管，连续管与可缠绕接头并未产生相互作用力；当环压深度为2.0 mm时，作用力集中于连续管与可缠绕接头之间；当环压深度为2.6 mm时，连续管受环压轮和快速接头两者的相互作用。

图4为环压深度2.6 mm、压轮半径分别为5.5和6.0 mm时，压接接头Mises应力云图。从图4可以看出，当环压深度为2.6 mm时，不同半径环压轮压接接头最大Mises应力位置相同。

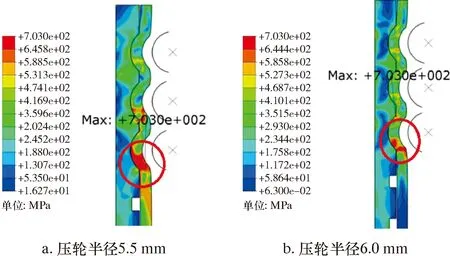
图4 环压深度2.6 mm时不同压轮半径环压Mises应力分布Fig.4 Distribution of Mises stress during circumferential crimping with different radius of circumferential crimping rollers at 2.6 mm circumferential crimping depth

3.2 环压深度对接头拉伸性能的影响

环压轮半径4.5 mm时环压至1.6、2.0及2.6 mm深度，400 MPa拉应力作用下拉伸应力云图如图5所示。环压深度分别为1.6和2.0 mm时，接头拉应力作用于环压轮(见图5a和图5b)；环压深度2.6 mm时，连续管环压至贴合，拉应力集中于连续管最后一个环压轮(见图5c)，易在最后一个环压轮部位产生应力集中导致连续管断裂。

图5 环压轮半径4.5 mm时不同环压深度最大Mises应力分布Fig.5 Distribution of maximum Mises stress of different circumferential crimping depths at 4.5 mm circumferential crimping roller radius

分析可知，在选择连续管环压深度时，应避开导致接头产生应力集中的环压深度，使拉应力均匀分布于压接接头3个环压槽凹槽部位，以提高连续管接头使用性能。

图6为环压深度1.8 mm，拉应力400 MPa时，压接接头最大拉应力位置。从图6可以看出，相同环压深度，不同环压轮半径环压，拉伸应力集中位置相同，均位于可缠绕接头第一个环压轮与可缠绕接头接触部位两端部。结合图4得到，环压深度一定，连续管最大应力集中位置相同。

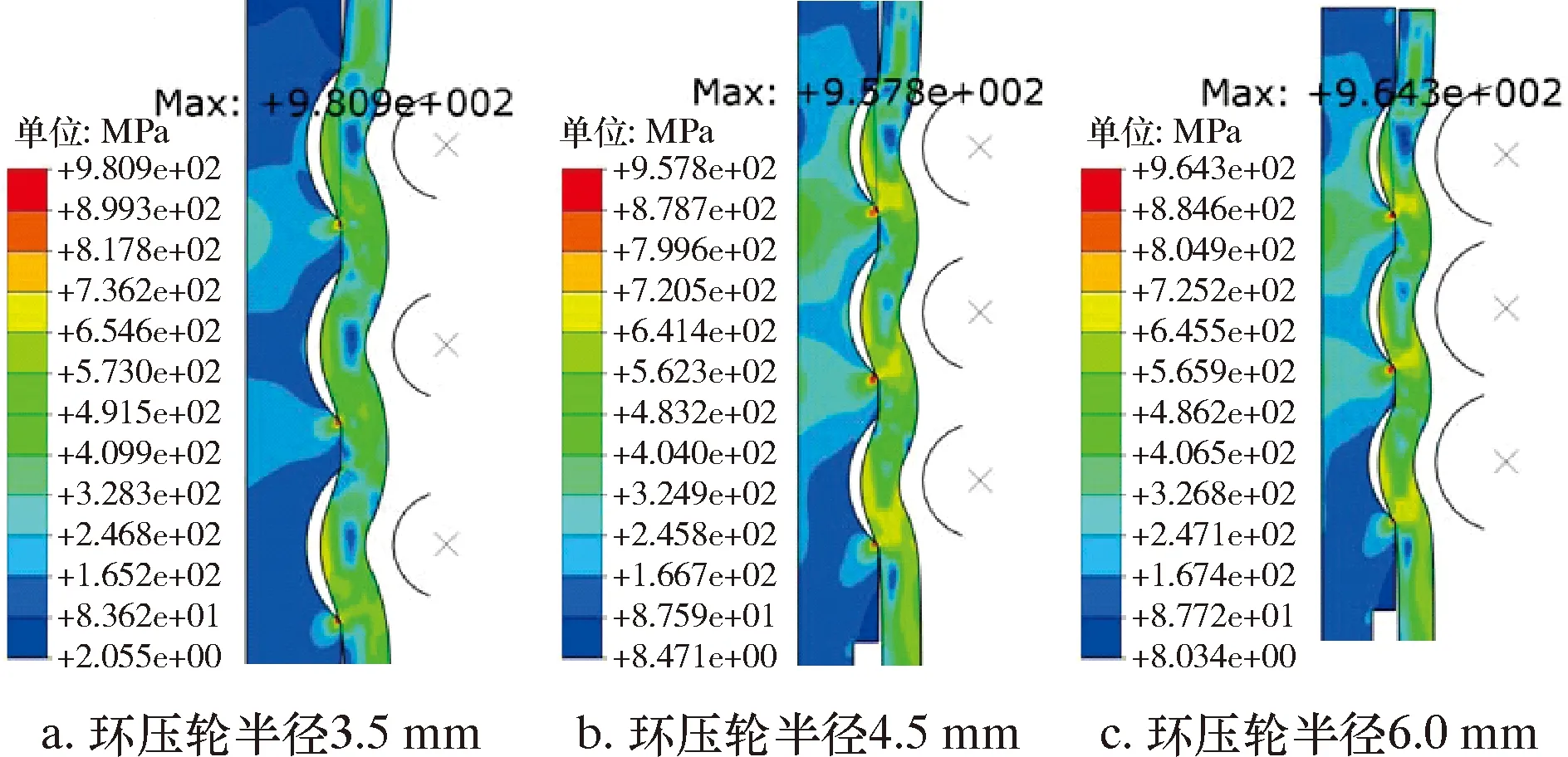
图6 环压深度1.8 mm时不同环压轮半径环压最大Mises应力分布Fig.6 Distribution of maximum Mises stress during circumferential crimping with different radius of circumferential crimping rollers at 1.8 mm circumferential crimping depth

3.3 环压轮半径对压接接头Mises应力的影响

采用环压深度2.2 mm，环压轮半径3.5、4.0、4.5、5.0、5.5及6.0 mm对连续管、可缠绕接头进行环压，得到环压轮半径对压接接头Mises应力的影响，结果如图7所示。

由图7可以看出，随着环压轮半径的增加，压接接头最大Mises应力呈现出先增加后减少再增加的趋势，环压轮半径4.5 mm时最小。

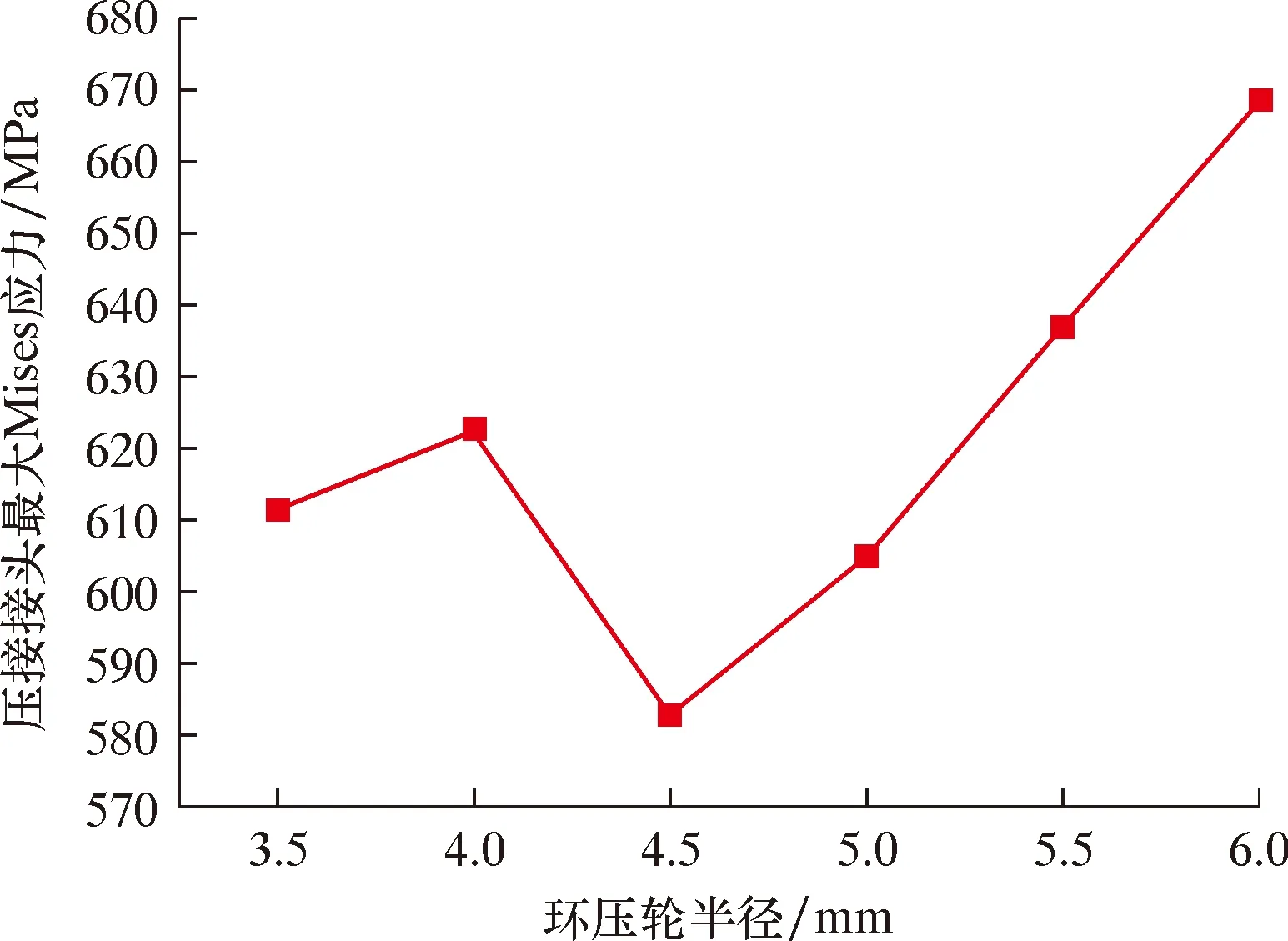
图7 环压深度2.2 mm时不同半径环压轮压接接头Mises应力Fig.7 Mises stress of crimping joint of different radius of circumferential crimping rollers at 2.2 mm circumferential crimping depth

图8为环压深度2.2 mm，环压轮半径3.5、4.5和6.0 mm时，连续管表面Mises应力分布图。从图8可以看出：当环压轮半径为3.5 mm时，连续管凹槽底部Mises应力最大；随着环压轮半径的增加，当环压轮半径为4.5 mm，压接接头Mises应力分布较均匀，平均应力较低；当环压轮半径为6.0 mm时，压接接头最大Mises应力出现在连续管表面。环压深度相同时，环压轮尺寸决定压接接头应力分布状态。

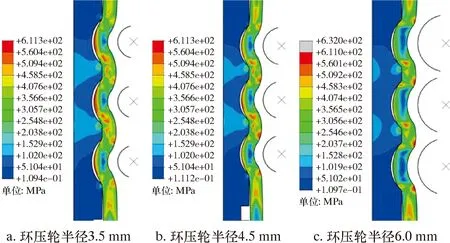
图8 深度2.2 mm时不同半径环压轮环压Mises应力分布Fig.8 Distribution of Mises stress during circumferential crimping with different radius of circumferential crimping rollers at 2.2 mm circumferential crimping depth

3.4 环压轮半径对接头Mises应力的影响

图9为不同环压轮半径环压时，接头轴向拉伸最大Mises应力变化趋势。

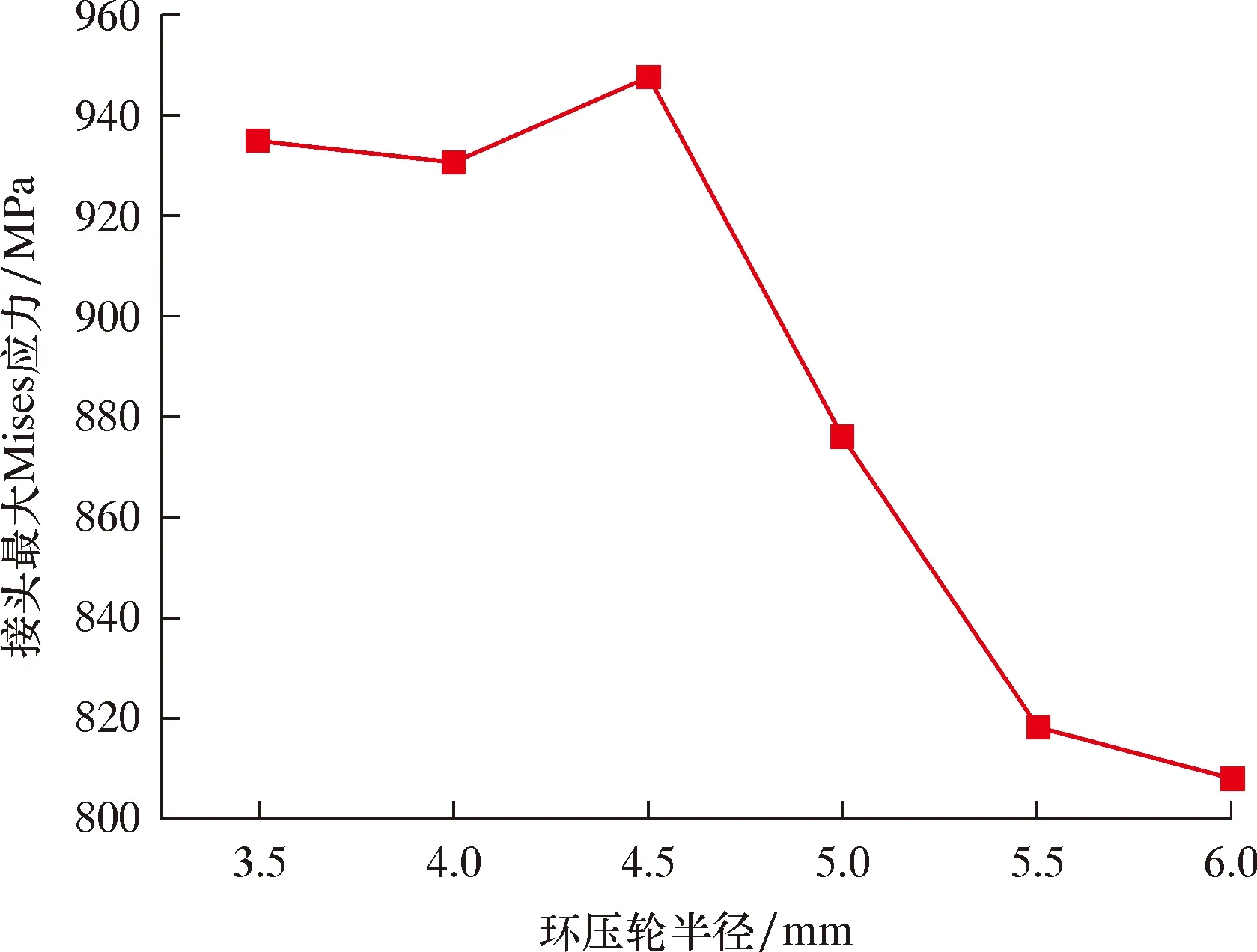
图9 环压深度2.2 mm时不同环压轮半径压接接头最大Mises应力Fig.9 Maximum Mises stress of crimping joint of different radius of circumferential crimping rollers at 2.2 mm circumferential crimping depth

对比图7和图9可以得到，接头环压最大Mises应力与接头拉伸最大Mises应力呈相互对应关系，即连续管环压后残余应力值越小，接头抗拉强度越高，符合材料变形规律。

3.5 环压深度和环压轮半径优选

采用不同半径环压轮压接连续管至不同深度，并对环压接头进行400 MPa拉伸，得到接头最大承载力，如表2所示。对表2进行分析，可以优选连续管最佳环压参数环压深度及环压轮半径。

由表2数据得到，接头拉伸强度与环压深度不呈正相关。对环压和拉伸过程分析可知，连续管接头失效或可能失效的原因如下：①环压深度1.4 mm，环压轮半径3.5、4.0及4.5 mm时，压接接头最大Mises应力达到连续管抗拉强度，此类点为环压可能失效点；②环压深度2.6 mm，环压轮半径5.0、5.5及6.0 mm时，连续管受压轮、可缠绕接头双重作用，压接接头所受Mises应力大于或等于连续管抗拉强度，如图4红色区域，环压直接导致连续管失效；③表2中部分接头抗拉强度达980 MPa，达到可缠绕接头屈服强度，接头最大拉伸强度位于可缠绕接头环压槽两端。接头使用过程中，此类应力集中点可导致可缠绕接头接触区域发生变形。因此，在环压深度选择时，应避开此类环压深度(1.6、1.8及2.0 mm)。

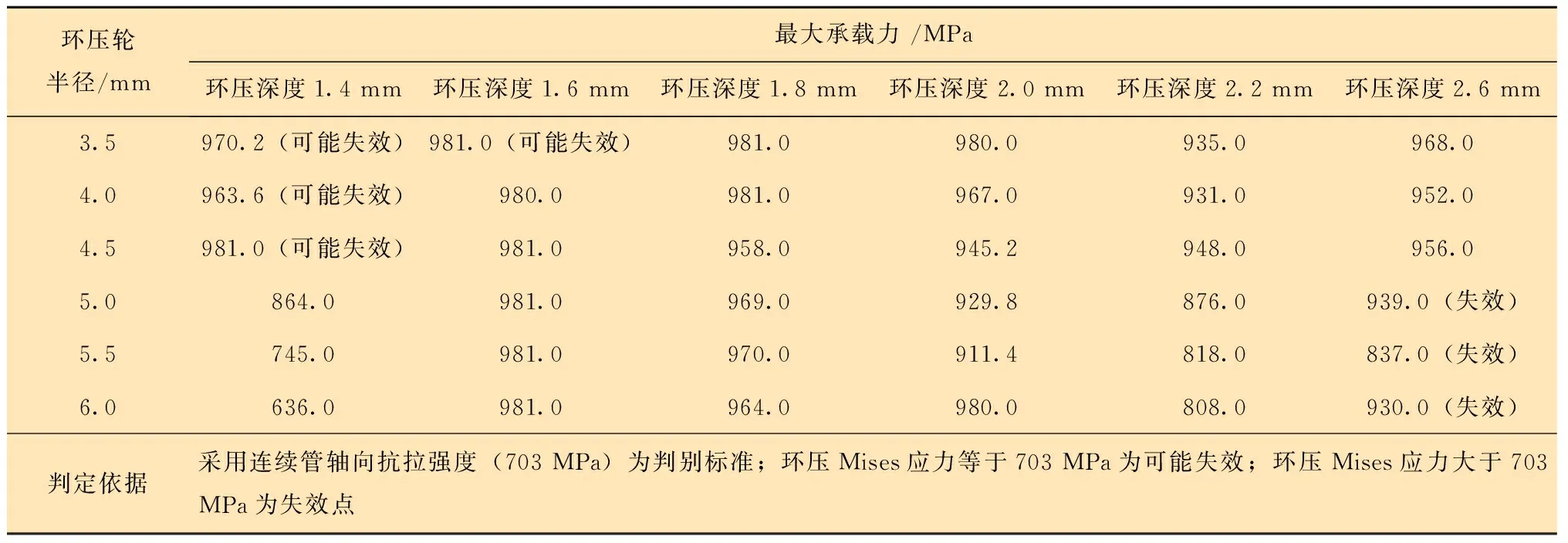
表2 400 MPa拉应力作用下接头最大承载力Table 2 Maximum bearing capacity of joint under 400 MPa tensile stress

针对ø38.1 mm×3.0 mm连续管环压，环压深度不能选择1.4 mm浅环压深度，也不能选择2.6 mm完全贴合环压深度。环压深度选择时，应避开连续管环压和拉伸过程产生的应力集中，优选环压深度2.2 mm较合适。 故优选环压深度2.2 mm、环压轮半径4.5 mm进行环压。

4 试验分析

对环压后连续管与可缠绕接头进行破坏性剖析，由于应力释放，连续管与可缠绕接头应力变化，连续管环压后应力测量较困难，本文采用连续管与可缠绕接头环压实际间距ab、cd、ef与模型测量数据对比的方式进行模型验证。

图10为连续管实际环压深度1.43、1.50及1.44 mm情况下实物局部剖面图。

图10 实际剖开测量位置Fig.10 Measurement position in physical profile

环压次序为图中所示1-2-3环压顺序，试验采用测深仪对环压后环压深度进行测量，得到实际环压深度；采用游标卡尺对环压完成后底部a、c、e内径，b、d、f外径进行测量，每组数据测量3次取平均，计算得到实际环压ab间隙、cd间隙及ef间隙，采用实际测量数据与建模数据对比。

图11为实际测量底部间隙与建模底部间隙对比图。图11中横坐标为次序号，纵坐标为底部间隙值。由图11可知，不同环压深度环压后连续管与可缠绕接头底部间隙与建模测量间隙基本一致。

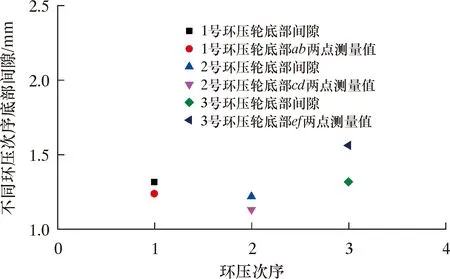
图11 实际测量与建模底部间隙对比Fig.11 Comparison of bottom clearance between actual measurement and modeling

5 结 论

(1)不同环压深度，接头抗压接和拉伸机理不同；环压深度决定接头最大Mises应力和拉应力分布位置；相同环压深度，环压轮半径决定压接接头应力分布状态。

(2)接头拉伸强度与环压深度不呈正相关，环压深度选择应避开压接接头Mises应力集中和拉伸应力集中导致的连续管或可缠绕接头失效点。

(3)针对ø38.1 mm×3.0 mm连续管环压，优选环压深度2.2 mm、环压轮半径4.5 mm，此时压接接头抗拉强度较高。