公路空间曲率连续性衰退与事故频数影响关联模型

王晓飞 刘永 李思雨,2

(1.华南理工大学 土木与交通学院，广东 广州 510640；2. 广东省现代土木工程技术重点实验室，广东 广州 510640)

交通事故致因是多方面的，通常可归为人、车、路和环境4大类，但是线形设计是否合理是关系到公路安全的根本性问题[1]，直接影响到车辆运行安全[1]。汽车行驶轨迹是一条连续的空间曲线，具有曲线、曲率及曲率变化率的连续性[2]，“曲率连续性”是公路线形设计理论中的基本原则和要求[3- 4]。提高线形设计的合理性，以满足实际行驶所需的安全速度、视距等要求,从而提高交通安全是十分必要的。

然而，传统平纵组合设计方法中，即使平纵断面内曲线分别连续和光滑，但组合后的空间路线连续性存在曲率跳跃现象[5]，造成空间曲率连续性的衰退，即曲率、曲率变化率不连续。受平纵分别设计的影响,Hassan、孟祥海等[6- 7]采用统计回归分析方法对现有二维平面线形几何要素与交通安全之间的关系进行研究，发现平面线形的突变会引起运行速度的突变，进而引发交通事故；陈永胜等[8]建立了纵面设计要素以及相关的要素组合、衔接方式的微观事故预测模型；赵一飞等[9]通过数据收集和分析，建立了包括竖曲线半径和长度等纵断面线形指标与交通事故率的关系模型；王福建等[10]进行了详细研究，发现不同平纵组合线形的事故伤亡程度并不相同，其中平凹组合最高，平凸最低；Zhang等[11]对于道路线形和正面碰撞事故的相关性研究表明,增大平纵曲线半径能有效降低交通事故率。这些研究基本都从平面、纵断面分别进行，即使在数值上进行一定的组合，并不能准确全面地反映公路线形在三维空间中的真实特性。

为弥补当前平纵横组合设计和评价方面缺乏的行之有效的量化方法和指标问题，从而为平纵组合而成的空间线形优化设计提供必要的理论依据，本课题组从三维角度出发提出表征公路三维线形的空间曲率、挠率等指标，并根据高等数学几何中曲线空间曲率的计算方法进行计算，根据国内线形及事故数据，采用统计回归分析方法对公路三维线形指标与交通安全之间的关系进行研究[12- 16]。由此可见，公路线形空间参数中空间曲率连续性衰退与交通安全存在明显的相关性。

为深入分析线形连续性衰退对交通事故的影响机理和影响模式，课题组收集了大量美国华盛顿州州际公路的设计资料及事故资料，应用负二项回归等模型，分析空间线形连续性衰退对公路交通事故的影响，建立空间曲率连续性与事故频数的关系模型。

1 公路三维线形曲率连续性表征参数

1.1 空间曲率

曲率是一个表示曲线弯曲程度的量，一般用k表示，即通过微分来计算空间曲线上某点的切线方向角对弧长的转动率来反映曲线偏离直线的程度。通常采用以下的通用曲线参数方程来计算曲率：

(1)

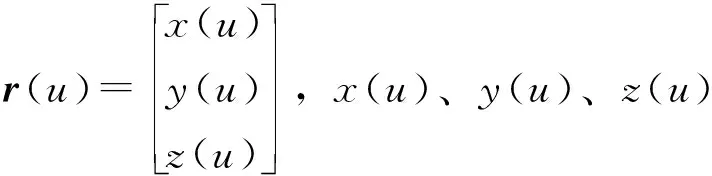
为了对平面线形以及纵面线形组合的曲率进行计算，传统公路平纵组合设计后有6种类型，见表1。华盛顿州从2018年起，对新建公路的缓和曲线设置不做要求，本次收集的州际公路中均未涉及缓和曲线。因此，平纵组合类型仅有表1中1-4这4种类型。

在道路线形的坐标系统中，平面坐标(x，y)可以用一个参数方程来进行表示:

表1 平纵线形组合类型Table 1 Horizontal and vertical alignment combination types

(x，y)=(x(l)，y(l))

(2)

式中,l为桩号，x(l)与y(l)为关于桩号l的参数方程。

该参数方程是一个分段的函数,x(l)与y(l)在不同的直线段区间、圆曲线段区间内表达式不同。

曲线段上的(x，y)均可以根据每个曲线单元的起点o的里程值lo、终点e的里程值le进行计算，线段内一点q的计算里程为l=lq-lo，曲率为k；曲线段里程长S=le-lo。建立如图1所示的临时坐标系，由此进行平曲线坐标的计算。

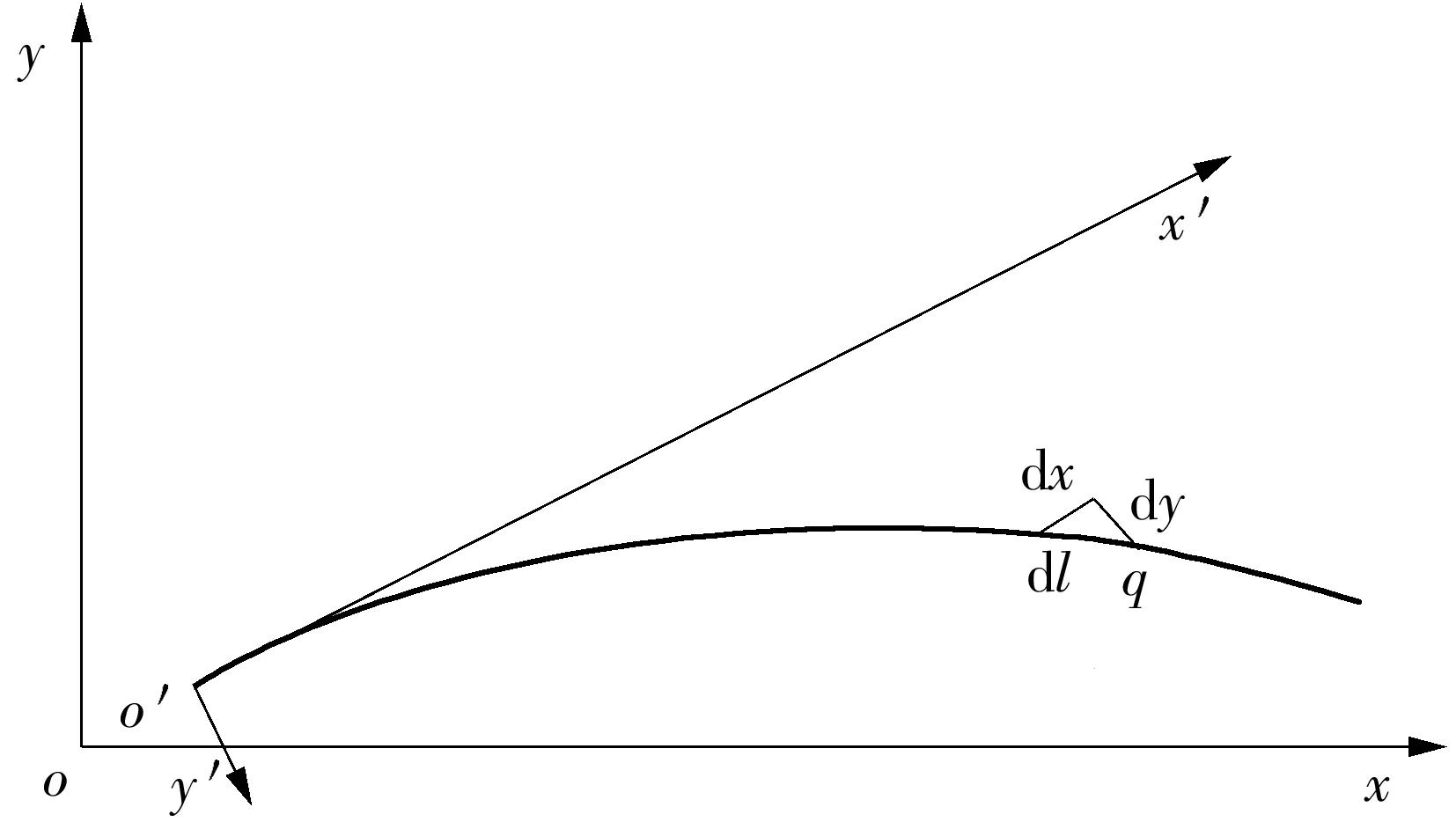
图1 平曲线坐标的计算Fig.1 Calculation of horizontal curve coordinate

(1)直线段

此时在以该段直线的起点o′为原点，以直线的延伸方向作为x′轴，垂直直线方向作为y′轴，建立临时坐标系x′o′y′，计算得到：

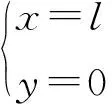
(3)

(2)圆曲线段

此时在以圆曲线的起点o′为原点，以圆曲线在o′点的切线方向作为x′轴，其法线方向作为y′轴，建立临时坐标系x′o′y′，计算得到：

(4)

式中：R为圆曲线的半径。

在竖曲线设计中，一般采用二次抛物线作为竖曲线。竖曲线是由直线段、曲线段组合形成的。相关定义为：线段内一点q的曲线长变量l=lq-l0；高程为h，路段起点高程为h0；坡差w=i2-i1，i1、i2分别路段起终点纵坡值；曲线段长S=le-l0。建立如图2所示的loh临时坐标系，进行竖曲线坐标的计算。

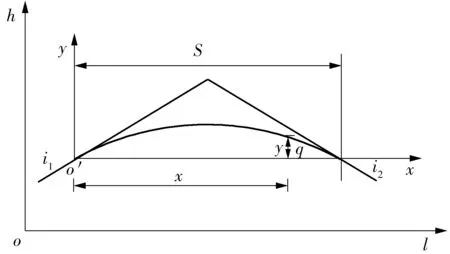
图2 竖曲线坐标的计算Fig.2 Calculation of vertical curve coordinate

(1)纵坡段

易知直线段有

h=h0-i1l

(5)

(2)竖曲线段

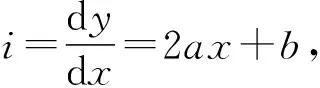
(6)

式中Rv为竖曲线的半径。

由于平面线形和纵面线形起点并不重合，为了进行参数的统一，引入l作为路段上任意一点到该路段起点的距离，引入la作为路段起点到该路段所属平面线形的起点的距离，引入lb作为路段起点到该路段所属纵断面线形的起点的距离，引入Rh作为平曲线半径。因此4种线形组合关于弧长l的参数方程如下。

(1)对于TL组合线形，

r(l)=[(l+la),0,h0+i1(l+lb)]

(7)

(2)对于TV组合线形,

(8)

(3)对于CL组合线形，

(9)

(4)对于CV组合线形，

(10)

分别对以上4种路段计算空间曲率，将式(7)代入式(1)得到,TL组合下,

k=0

(11)

将式(8)代入式(1)得到TV组合下：

(12)

将式(9)代入式(1)得到,CL组合下,

(13)

将式(10)代入式(1)得到,CV组合下,

(14)

根据式(11)-(14)及公路线形数据，可计算出TL、TV、CL、CV 4种线形组合下的各点的曲率值。

1.2 平均曲率

在路段内等分取n个点，将n个点曲率的平均值作为该路段平均曲率。

(15)

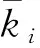
1.3 相邻路段曲率差绝对值

按照桩号增加方向为后一个路段，将相邻路段曲率差绝对值分为与前后相邻路段曲率差绝对值，公式如下。

(1)与前一个相邻路段曲率差绝对值为

(16)

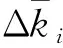
(2)与后一个相邻路段曲率差绝对值为

(17)

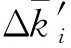
2 数据准备

2.1 数据来源

本研究的数据来自于华盛顿州的5条州际公路2011年1月至2018年7月发生的事故及线形数据，分别为5号公路K0+500—K445+000路段、90号公路K3+400—K323+000路段、182号公路K0+500—K22+800路段、205号公路K42+800—K60+200路段、405号公路K0+000—K48+400路段。图3为5号公路K1+000—K4+000路段的空间线形曲率图。由图可见，3 km内存在多处跳跃。

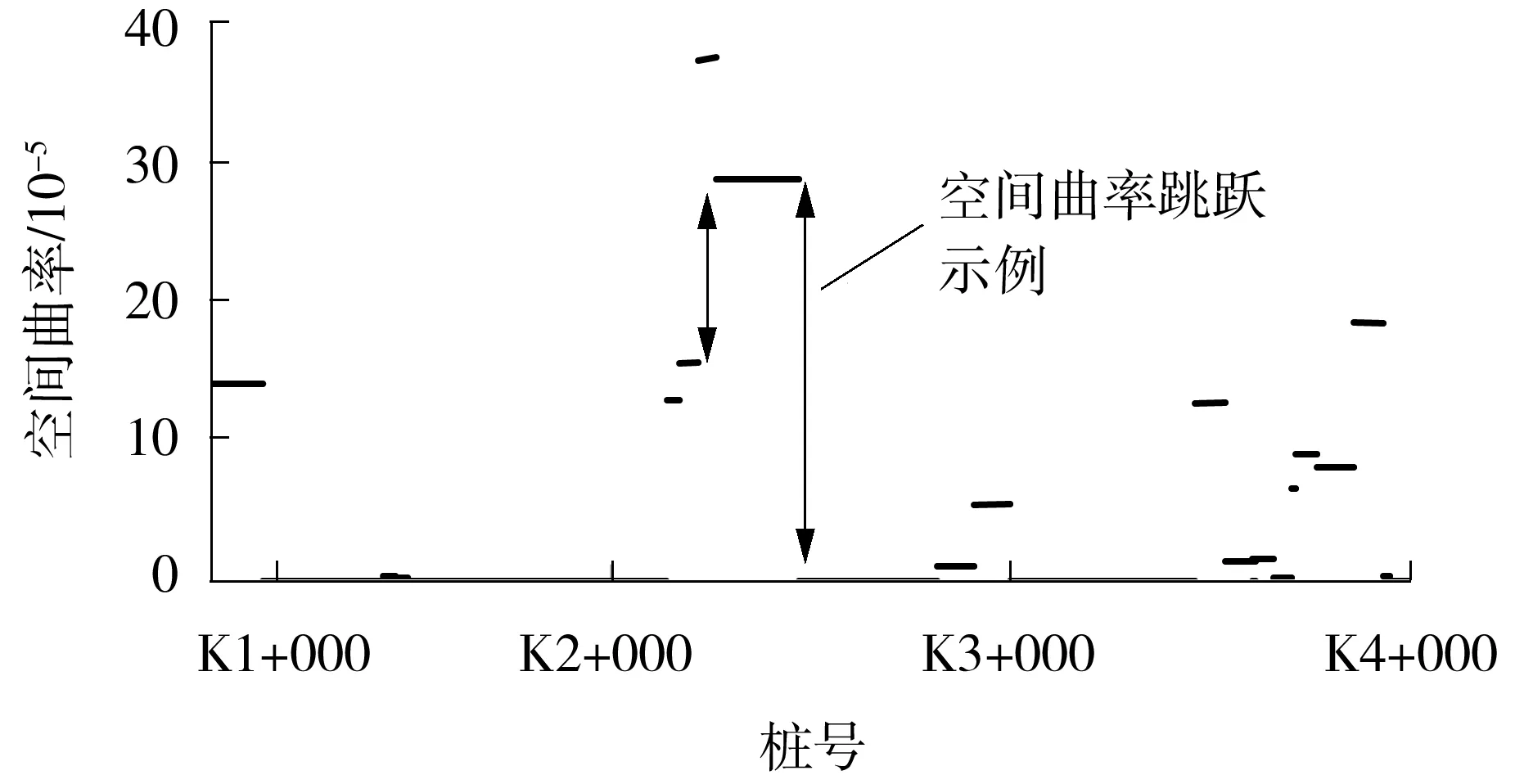
图3 5号公路K1+000—K4+000路段空间曲率跳跃图

2.2 路段划分

路段长度划分是建立高速公路交通事故数据分析模型的先决条件，直接影响到模型拟合精度以及模型的应用效果。相关文献已证明事故频次和路段长度是线性相关的，且在多种类型的道路交通安全分析中也得到了验证[17- 18]。

为确定合适的路段长度单元，根据表1中TL、TV、CL、CV 4种组合类型的特点，对华盛顿州的5条州际公路线形按不同组合类型分成6 658个路段后对路段长度进行描述统计。发现路段长度平均数和中位数分别为122.72 m和103.39 m，其峰度值为7.202，数据分布较集中，偏度值为2.159 6，表明路段长度的分布为高度向右的偏态分布。对于平纵组合分段路段长度这种程度较大的偏态分布，若选用平均数作为集中趋势的代表值，易受较长的路段长度极端值的影响，中位数对数据的集中趋势测度值有更好的代表性，因此路段长度较集中于103.39 m。

此外，根据规范上定义停车视距作为安全所需视距，提出2.5～3.0 s为驾驶员从发现危险到改变操纵行为以保证安全所需的时间，以及考虑到美国州际公路的限速普遍在90～120 km/h，3 s行程距离计算约为100 m。因此本研究在对连续型衰退的影响分析中，综合考虑线形数据中平纵组合特点及驾驶员的操作特性，选取100 m为定长进行路段划分，得到8 512个路段。

2.3 数据统计与分析

进行路段划分后将统计年限内每百米路段事故频数进行统计，在统计事故数据时剔除雨雪天、雾天、不良路面状况、交叉口路段、匝道路段、酒驾等与道路线形特征无关的因素造成的事故频数，以更好地研究线形三维曲率及其变化与公路交通事故发生数的相关性。路段事故数据统计结果见表2，路段事故总数频率见图4。由表2和图4可知：8 509个路段中事故数的方差大于平均值，有3 012个路段事故发生总数为0，为对比分析，对这些事故进行了初步筛选，其中5 497个路段至少发生了一起事故，将该数据称为零截尾数据，零截尾数据中事故数的方差也大于平均值。

表2 百米路段事故数据统计Table 2 Statistics of highway 100 meters unit accidents

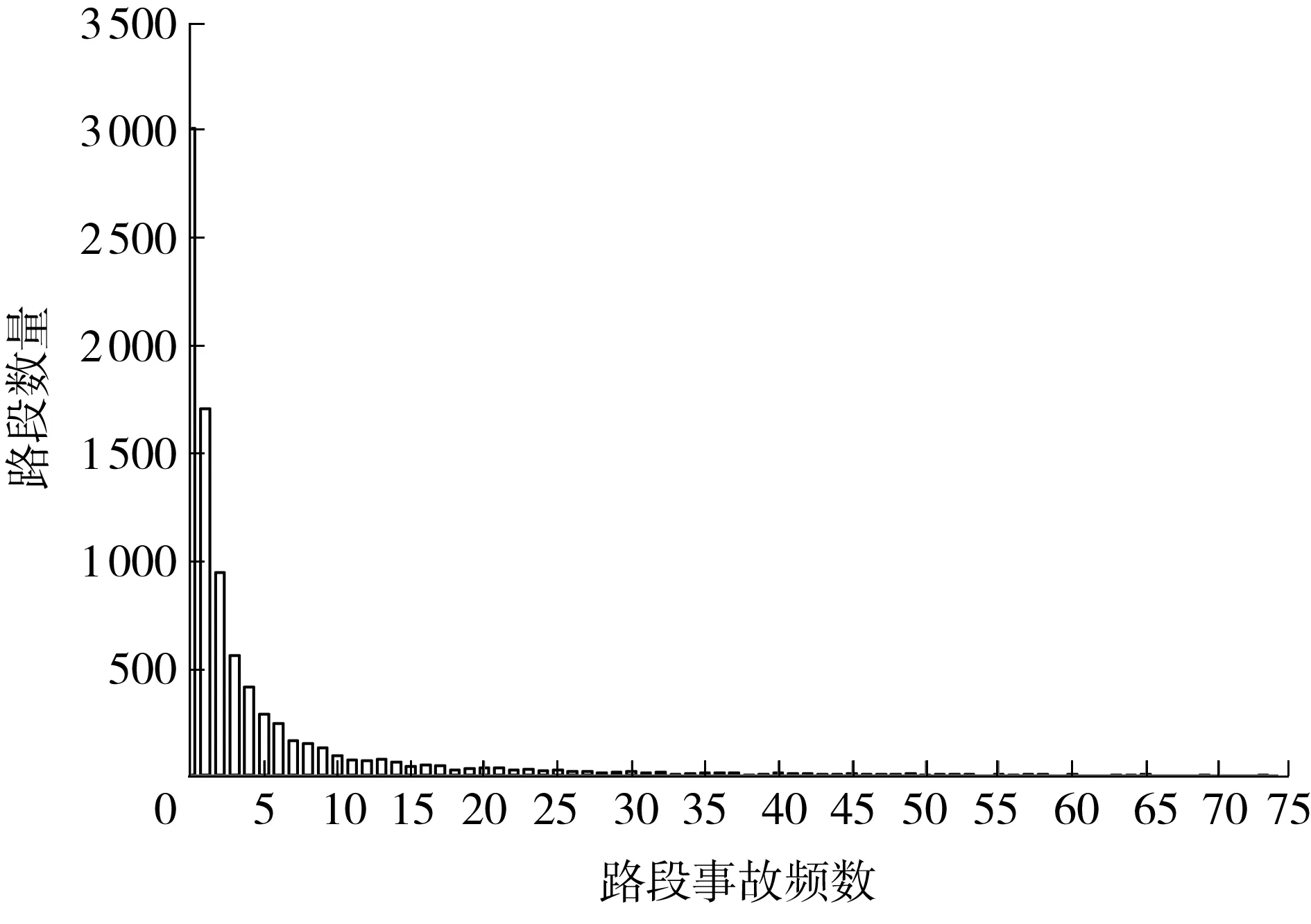
图4 百米路段事故频数频率图

3 模型选取与构建

3.1 模型构建

3.1.1 负二项模型

以事故频数为因变量来建立事故分析模型或预测模型时，由于事故数为非负整数的计数数据，在统计上常使用泊松回归进行模型估计。然而，泊松回归的局限是它要求期望和方差相等，如果方差明显大于期望，即存在“过度分散”时，Burger等[19]提出一个修正的泊松回归方法来进行模型估计，即负二项回归(NB)。根据数据分析，本研究中被解释变量路段事故全数据及零断尾数据的方差显著大于均值，数据过离散，因此可采用NB模型进行本研究的模型估计。

负二项分布是一个连续的混合泊松分布，其允许泊松均值服从γ分布。用随机变量T定义负二项分布，其中r为独立重复实验中失败的累计出现次数，t为随机变量，表示成功实验次数，其概率分布表达式如下：

(18)

(t=0,1,…)

3.1.2 零膨胀负二项模型

当被解释变量的样本数据中含有较多的零值，则要考虑使用零膨胀负二项回归(ZINB)估计。根据数据过离散、含较多的0值的特点，可采用ZINB模型进行全数据的模型估计[18]。

零膨胀负二项分布实际上是基于零分段建立的一个混合的概率分布，由一个负二项分布和一个离散分布组成，公式如下：

(19)

(20)

式(20)包括了一个计数模型和用logit估计的膨胀模型。式中，αi、δi为回归系数，wi是第i个解释变量。

3.1.3 零截尾负二项模型

负二项模型虽然已经广泛应用于多个领域，但是该模型需要完备的观测数据[20]。受实际状况所限，研究人员可能无法获取完备的数据，如前文所述的仅有事故发生路段的数据。在这种情况下传统负二项模型不能有效地描述变量与自变量之间的关系。为此，则可以考虑零截尾的计数分布模型。零截尾的计数分布模型可以视为原计数模型的条件分布模型，即观测变量均为自然数。零截尾负二项分布模型(ZTNB)可以理解为传统负二项模型在非负条件下的分布模型。根据截尾数据仅包括事故数均为正整数、过离散的特点，可采用ZTNB模型对截尾数据进行模型估计。

零截尾负二项分布模型概率分布表达式如下：

(21)

在模型拟合优度检验和对比方面，本研究采用了赤池准则(AIC)、贝叶斯准则(BIC)对不同模型进行检验和比较，当模型样本数据相同时，AIC和BIC值越小，则模型对数据的拟合越好。对于ZINB模型和NB模型的对比，还可采用Vuong检验，Vuong检验值为正，则更适合使用ZINB模型，反之则适合使用NB模型。由于AIC和BIC仅适用于样本相同模型间的比较，而本研究对全数据和零截尾数据2种数据分别进行了分析，所以两种样本间模型的拟合效果不能通过AIC、BIC值进行对比。

3.2 模型结果

首先进行共线性诊断和模型合理性判定。为提高模型模拟的精度，需尽可能地排除具有强相关关系的解释变量，为此建模前要进行多重共线性诊断。

本研究利用方差膨胀因子(VIF)、容差和条件索引对所选取的解释变量进行诊断。通常认为出现下列情况之一则表示存在多重共线性：最大的VIF超过10；容差小于等于0.1；条件指标大于10。对解释多重共线性检验的结果见表3。诊断发现，本研究所选取的变量的VIF最大值为1.697，最小容差值为0.589，最大条件指标为2.572，说明它们之间没有明显的共线性。

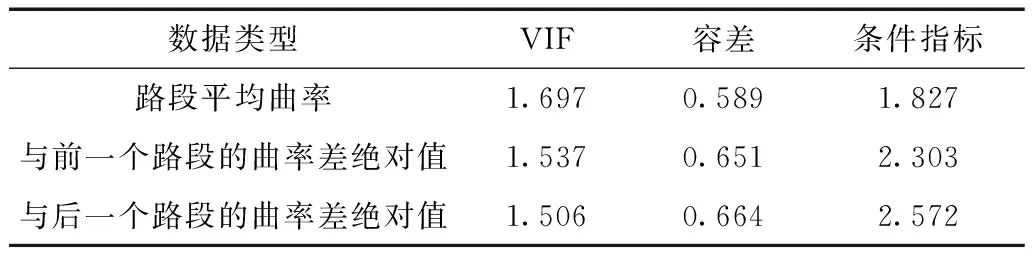
表3 描述变量多重共线性检查Table 3 Descriptive variable multicollinearity check

根据数据类型和特点，分别建立以下模型：模型1，对全数据使用传统负二项模型进行拟合；模型2，对全数据应用零膨胀负二项回归模型进行拟合；模型3，对零截尾数据使用传统负二项模型进行拟合；模型4，使用零截尾负二项模型对零截尾数据进行拟合。对4个模型进行拟合优度检验和对比分析，结果见表4。

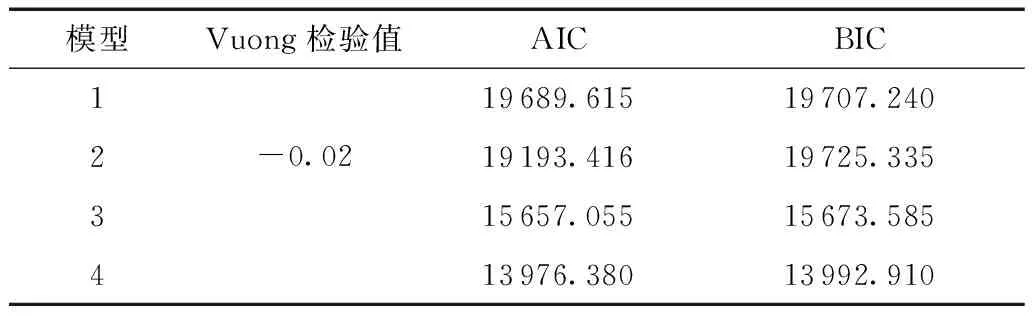
表4 模型检验结果Table 4 Model test results

表4结果表明，由于AIC和BIC仅适用于样本相同模型间的比较，模型1、模型2和模型3、模型4的样本不同，不能同时比较。因此分别对同样本的模型进行对比，从表中结果来看，在基于全部数据的回归模型1和模型2中，模型2与模型1的AIC、BIC值相差不大，模型2的Vuong检验值为接近0的负数，说明两个模型有相似的拟合度。比较模型3和对比模型4均基于零截尾数据，可以采用AIC和BIC对其优劣性进行对比分析，模型4的AIC、BIC值均小于模型3，拟合度更优。

进一步对4个模型进行参数估计，计算各模型结果见表5。表中，cons表示常数，Coef表示系数，Std Err表示标准误。

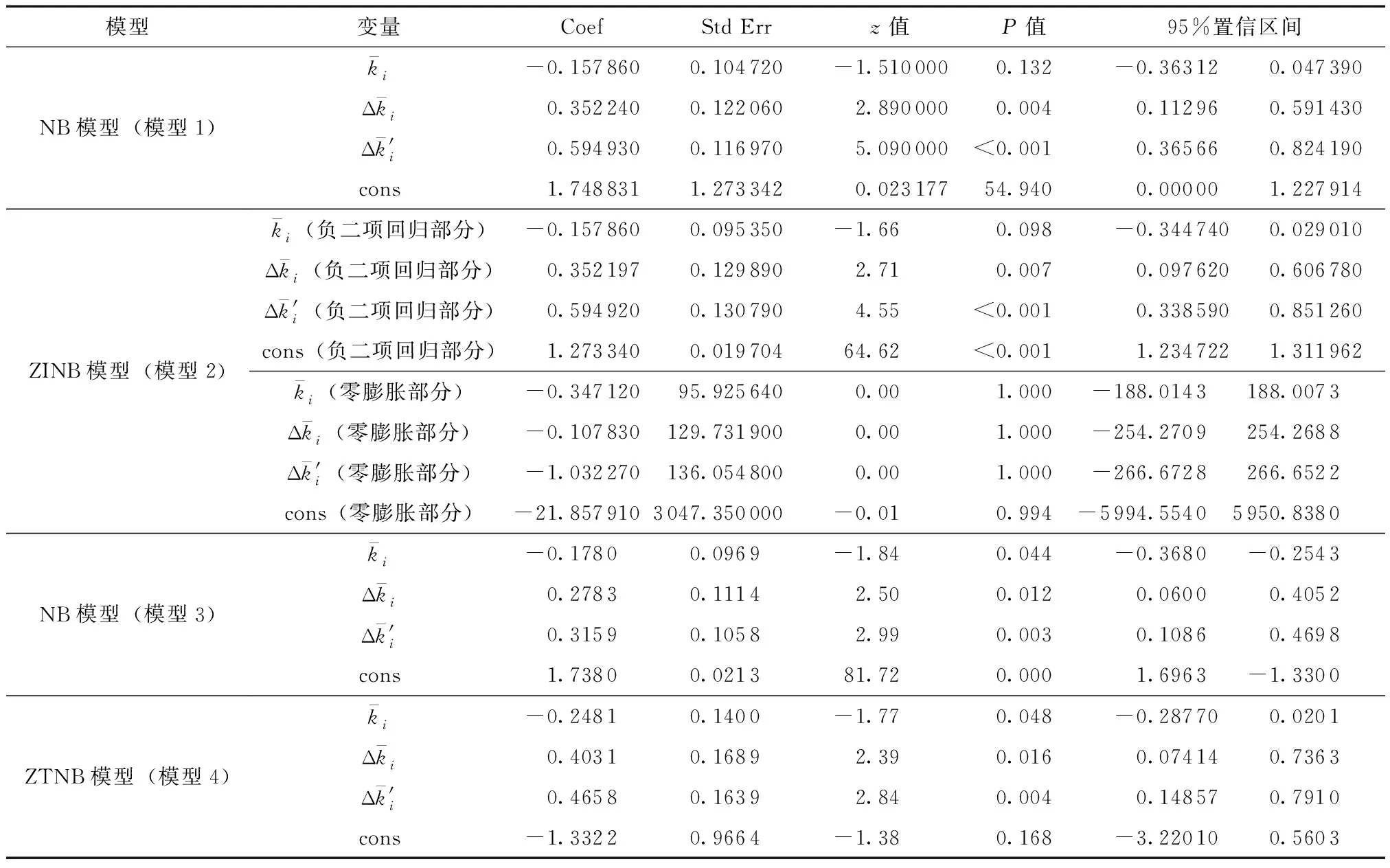
表5 模型回归系数估计结果Table 5 Regression coefficient estimation results

从表5中可以看出，模型1中与前、后一个路段曲率差绝对值的估计值的显著水平均高于95%，系数均大于0，表明随着与相邻路段曲率差绝对值的增加，路段的事故频数增加，且与后一个路段的曲率差绝对值的影响程度高于与前一个路段的，路段平均曲率的影响不显著。模型2的零膨胀部分的影响不显著，而负二项部分影响路段事故发生频数的3个因素中，与前、后一个路段的曲率差绝对值的影响显著，系数分别为0.352 197与0.594 92，说明与相邻路段曲率差绝对值的增加会导致事故数量的增加，其中与后一个路段的曲率差绝对值是主要影响因素。在模型3中，3个自变量对被描述变量的影响均显著。其中，前、后相邻路段的曲率差绝对值的系数分别为0.278 3、0.315 9，说明在发生事故的路段中，相邻路段曲率差绝对值的增加会导致事故频数的增加，其中与后一个路段的曲率差绝对值是主要影响因素，而路段的平均曲率的系数为-0.178 0，即路段曲率的增加会一定程度地减少事故的发生。在模型4中，3个自变量对被描述变量的影响也均显著，路段平均曲率、与前后路段的曲率差绝对值的系数分别为-0.248 1、0.403 1、0.465 8，与模型3的相应系数方向(同为正或负)以及主要影响因素一致。

4 结论

通过对华盛顿州5条州际公路的线形及事故数据进行统计，建立负二项、零膨胀负二项、零截尾负二项回归模型，研究了空间线形连续性衰退对事故频数的影响。得到如下结论：

(1)传统平纵断面曲率连续的公路设计，存在三维空间上的曲率跳跃，会造成公路线形的连续性衰退现象。

(2)基于全数据的模型1和模型2的负二项部分中与前、后相邻路段曲率差绝对值对路段事故数影响显著，路段平均曲率对交通安全的影响不显著，而在零膨胀负二项模型中的零膨胀部分的3个描述变量，对被描述变量的影响均不显著，模型1比模型2拟合更优；基于截尾数据的模型3和模型4中，路段平均曲率、与前后相邻路段曲率差绝对值对路段事故数影响显著，模型4的AIC、BIC更小，拟合更优。

(3)相比于基于截尾数据的模型3和模型4，基于全数据的模型1和模型2的负二项部分中，由于大量零事故路段数据的增加，导致基于全数据的平均曲率对交通安全的影响不显著，而对于发生事故的路段的两个模型中，路段平均曲率对事故频数影响显著。在模型1、模型2的负二项部分、模型3和模型4中，与前、后相邻路段曲率差绝对值与道段安全水平之间均存在较大的正关联，即增加公路三维曲率的连续性能减小事故频数，提高交通安全性水平，与前、后相邻路段曲率差绝对值可以作为道路线形水平评价指标。

本研究所建立的事故频数分析模型中，统计了5条州际公路的线形及事故数据，在后续研究中还应进一步丰富线形组合，增加公路里程和数量，结合其他交通与环境因素以及驾驶人的生理和心理特性、驾驶行为等人的因素对车辆行驶安全的影响,逐步深入研究公路空间线形连续性衰退对交通安全的影响。