高速公路单车事故等级的影响因素分析

温惠英 张璇 曾强

(华南理工大学 土木与交通学院，广东 广州 510640)

高速公路作为我国综合交通运输系统重要的组成部分，其安全问题一直是道路交通管理部门和研究人员关注的焦点。其中，作为高速公路上一种典型的事故类型，单车事故对我国人民生命财产造成的威胁不容忽视。根据《2015年中华人民共和国道路交通事故统计年报》可知，2015年全国高速公路单车事故导致1 169人死亡，3 274人受伤，直接财产损失达7 190.9万元。因此，有必要对高速公路单车事故等级的影响因素进行深入研究，提出相应的安全改善措施，减少因该类事故导致的人员伤亡和财产损失。

国内外学者对高速公路单车事故的事故频次、发生概率和严重程度开展了相关的回归分析研究。Yu等[1]利用贝叶斯双变量对数正态泊松模型对美国科罗拉多州I-70州际高速公路的单车事故和多车事故频次进行联立建模，量化了道路、交通因素对这两类事故频次的影响。Wang等[2]针对上海一段45 km长的高速公路，建立贝叶斯双变量负二项条件自回归模型，在识别单车事故和多车事故的显著影响因素的同时，判别了该高速公路上这两类事故的多发路段。Dong等[3]采用混合logit模型对美国科罗拉多州I-25州际高速公路的单车事故发生概率进行了回归分析，结果表明平均车速、能见度和湿滑路面对单车事故发生概率具有显著影响。Hou等[4]基于2013—2017年黑龙江省4条高速公路的事故数据，采用均值异质性混合logit模型，分析了驾驶员特征(年龄、性别和驾龄)、车辆类型、道路属性(几何设计、路面条件、中央隔离带类型和地形地势)、环境因素(天气条件和照明情况)等对单车事故严重程度的影响。Wen等[5]针对2015—2017年发生在云南省山区高速公路上的3 037起单车事故，根据驾驶员居住地和事故地点间的距离，将驾驶员分为路况熟悉驾驶员和不熟悉驾驶员；并建立随机效应广义有序probit模型，分析了驾驶员年龄、性别,是否酒驾、是否系安全带,车龄、车辆类型、交通量、限速、天气条件、照明情况、事故时间和季节等因素对两类驾驶员伤亡严重程度的影响。

在上述高速公路单车事故严重程度研究中，虽已分析了人、车、路、环境相关因素的影响，但是却忽略了路政医疗救援对降低事故严重程度的作用。已有研究表明[6- 7]，及时的路政医疗救援能够有效减少交通事故人员伤亡。此外，在上述事故研究中，关于天气状况的相关记录仅有事故报告中对天气情况的简要描述(例如：晴、雨、雾等)。该类描述并不全面，缺乏对风速、温度等数据的准确记录。而且，大多数事故研究中的天气条件为交警在事故现场甚至通过事后回忆记录的，难以精准反映事故发生时的天气状况。采用气象部门通过气象传感器记录的实时风速、降水量、温度、湿度和能见度等气象指标数据能够弥补该不足。近年来，在事故研究中融合实时气象数据进行分析逐渐成为趋势[8- 13]。

基于以上分析，本研究探讨了高速公路单车事故等级的影响因素。即通过对路政部门和气象部门的调研，获取了广东省开阳高速公路2013—2015年的单车事故数据和实时气象数据。以事故等级为因变量，建立随机参数有序logit模型，分析包括驾驶员特征、车辆类型、事故时间、路政救援到达时长和实时天气条件在内的多个因素对高速公路单车事故等级的影响。基于模型分析结果，提出了降低该类事故等级的安全改善措施。

1 数据准备

本研究分析对象为2013年至2015年广东开阳高速公路的单车事故数据。广东开阳高速公路为G15沈海高速公路上衔接佛开高速和阳茂高速的一段，全长约为125.2 km。本研究使用的数据集由两部分组成：来源于广东交通集团路政管理平台的2013年至2015年开阳高速公路事故数据，该平台记录了每起事故的发生日期、时间、地点、事故等级、路政救援到达时长、事故类型、肇事车辆、肇事驾驶员等信息。根据事故类型，选择其中的单车事故数据，并剔除其中具有不完整信息的事故记录，共获得1 000起单车事故数据用于建模分析；由广东气候中心采集于气象信息管理系统的实时气象数据，具体为2013—2015年开阳高速公路沿线气象站(开平站、恩平站和阳江站)记录的小时风速、降水量、能见度、湿度和温度等指标数据。针对上述单车事故，按照事故地点和时间匹配每起事故发生时的风速、降水量、能见度、湿度和温度数据。

在广东交通集团路政管理平台中，交通事故按照严重程度从低到高依次被划分为轻微事故、一般事故、重大事故和特大事故4个等级，等级划分标准见表1。在所获取的1 000起单车事故中，包含214起轻微事故、758起一般事故、27起重大事故和1起特大事故。由于特大事故数量极少，本研究将其与重大事故合并为一个等级，即重特大事故，用于后续建模分析。

表1 事故等级划分标准Table 1 Crash severity classification standard

参考以往相关研究，从人、车、环境和救援等方面构建了11个自变量用于高速公路单车事故等级建模分析，具体包括：肇事驾驶员是否为职业驾驶员，肇事车辆是否为货车，肇事车辆牌照是否为外省牌照，事故是否发生在工作日和夜间，路政救援到达时长，事故发生时的实时风速、湿度、降水量、能见度和温度。这些自变量的定义和描述性统计量见表2。

表2 自变量定义及描述性统计Table 2 Definitions and descriptive statistics of independent variables

2 模型方法

2.1 模型结构

由于事故等级具有有序性，本研究的回归分析将以有序logit模型为基础。在传统的有序logit模型中，解释变量的系数是固定的。然而，在事故数据中，存在许多无法被观测到的要素，如事故发生前驾驶员的心理状态、行为和车辆的特性等，这些要素可能会对事故等级产生影响，或与已被观测到的解释变量相关，从而产生异质性。在建模中忽略异质性可能会导致参数估计的偏差。随机参数有序logit模型可以作为解决该问题的有效手段。随机参数有序logit模型基于传统有序logit模型的框架，放宽了对变量系数的限制，允许变量的系数变化，从而降低因异质性带来的估计偏差[14]。第2.1.1节与第2.1.2节分别对有序logit模型和随机参数有序logit模型进行介绍。

2.1.1 有序logit模型

在有序logit模型中，对于第i起事故，定义事故等级倾向zi与解释变量Xi间存在线性关系，即

zi=βXi+εi

(1)

式中，β为与观测因素Xi有关的待估计参数向量,εi为随机扰动项，假定服从logistic分布。

在此基础上，观测到的事故等级yi，可被定义为

(2)

式中，j∈{0,1,…,J},表示从最低(轻微事故)至最高(重特大事故)的事故等级。阈值μ0，μ1，…，μJ-1表示不同事故等级之间的阈值，其中，μ0的值为0。

由于误差项服从logistic分布，第i起事故的事故等级为j的累积概率计算方法如下:

(3)

因此，对于第i起事故，其事故等级为j的概率计算方法如下：

(4)

2.1.2 随机参数有序logit模型

在随机参数有序logit模型中，式(1)可改写成

zi=βiXi+εi

(5)

式中，系数βi定义为

βi=β+ωi

(6)

其中，ωi为服从均值为0、方差为σ2的正态分布随机项。

与第2.1.1节相似，在随机参数有序logit模型中，第i起事故等级为j的累积概率计算方法如下：

(7)

同理，第i起事故对应事故等级为j的概率计算方法如下：

(8)

2.2 模型估计

通过最大似然估计法，可估计得有序logit模型的参数结果。然而，由于随机参数有序logit模型系数的求解没有闭型解，仅能使用仿真求解。仿真求解涉及到随机抽样，而Halton序列抽样在随机抽样中的效果较好，因此本研究将使用Halton抽样对随机参数有序logit模型进行估计。根据文献[15]，Halton抽样次数为1 000时可满足需求。因此，本研究设定随机参数有序logit模型使用Halton抽样的次数为1 000。在分析过程中，本研究先基于表2的解释变量进行有序logit回归，再删除不显著的解释变量，重新进行有序logit模型回归和随机参数有序logit模型回归。

2.3 模型对比准则

本研究选择了赤池信息准则(AIC)和分类精度来评估模型对数据的拟合程度。其中，AIC的定义为

AIC=-2LL+2K

(9)

式中，LL为似然函数值，K为模型中拟合参数的数量。AIC值越小，说明模型拟合能力越优。

分类精度为在整个数据集的范围中，通过模型可准确预测事故等级的数量与数据样本量的比例[16]，其定义为

(10)

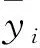
2.4 边际效应

边际效应的引入是为了说明变量变化(连续变量变化一个单位或分类变量由0变1)时相应的事故等级j的概率变化情况。

若xk为分类变量，对应事故等级j的边际效应为当变量xk为1时事故等级j的估计概率和变量xk为0时对应事故等级为j的估计概率的差值。

若xk为连续变量，变量xk对应事故等级j的边际效应为

(11)

3 模型结果

对有序logit模型和随机参数有序logit模型进行参数标定后，得到参数结果和模型拟合指标，见表3与表4。

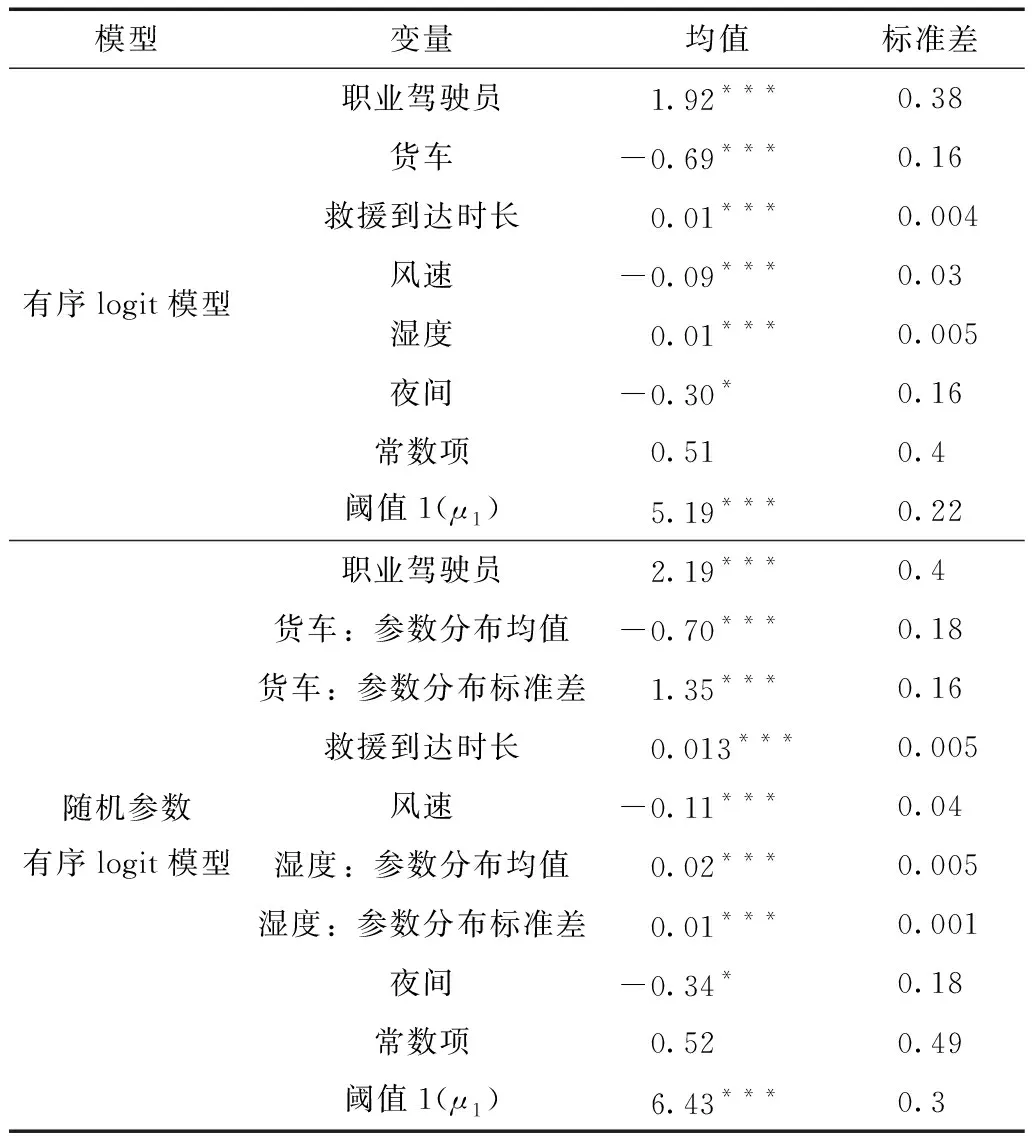
表3 模型结果1)Table 3 Model results

表4 模型对比参数Table 4 Model comparison parameters

3.1 模型比较

模型拟合指标显示：随机参数有序logit模型的对数似然值(越大越好)和分类精度均大于有序logit模型的对数似然值和分类精度，表明随机参数有序logit模型的拟合能力更优。

随机参数有序logit模型识别出“货车”和“湿度”两个变量对应的系数为随机参数(以上2个变量的系数均值和参数分布标准差在99%的置信水平上显著)。该结果表明，高速公路单车事故数据中存在异质性。异质性可能源于尚未被观测的变量，如驾驶员的行为或车辆事故前的状态等。

随机参数有序logit模型的数据拟合能力更优，且可有效识别异质性，均表明随机参数有序logit模型优于传统有序logit模型。

3.2 参数解释

在有序logit模型和随机参数有序logit模型中，以下变量在90%以上的置信水平上显著：职业驾驶员、货车、救援到达时长、风速、湿度和夜间。鉴于第3.1节的结论之随机参数有序logit模型更优，本研究将结合其边际效应结果(见表5)对参数进行解释。

相比于非职业驾驶员，职业驾驶员更易导致高等级的单车事故。当车主为职业驾驶员时，事故等级为一般事故和重特大事故的概率分别提高7.63%和6.22%，而轻微事故的概率降低13.85%。潜在原因为：相较于非职业驾驶员，职业驾驶员易在高速公路上行驶过长时间，疲劳驾驶的可能性较高，一旦发生单车事故，更可能引发严重的事故后果[17]。

关于肇事车辆类型对高速公路单车事故等级的影响，由表3可知，“货车”的系数服从均值为-0.7、标准差为1.35的正态分布，该系数小于0的概率为69.8%。该结果说明，相比于其他类型的车辆，在69.8%的高速公路单车事故中，货车发生高等级事故的倾向更低；相反，在另外30.2%的高速公路单车事故中，货车发生高等级事故的倾向更高。由其边际效应可知，综合而言，货车发生重特大事故的概率比其他车辆的低0.59%。这可能是因为货车相对于小汽车、长途客车等客运车辆的载客量更低、耐撞性更高[18]。

救援到达时长的增加将提高发生严重事故的概率。救援到达时长每增加1 min，事故等级为一般事故和重特大事故的概率分别增加0.14%和0.01%，轻微事故的概率减少0.15%。潜在原因为：救援到达时长的增加会导致单车事故中人员伤亡水平更严重。随着事故救援到达时长的增加，人员的伤亡情况倾向于从较轻的水平向严重的水平转化。其他研究中也可得到类似结论[19- 20]。

气象要素方面，风速和湿度都对单车事故等级有显著影响。当风速增加一个单位，单车事故的事故等级为一般事故和重特大事故的概率分别减少1.30%和0.10%，轻微事故的概率增加1.40%。潜在原因为：当驾驶员感受到风速增加时，会提高警惕，控制行驶速度，从而规避风险。湿度方面，由表3可知，湿度的系数服从均值为0.02、标准差为0.01的正态分布，表明该系数小于0的概率为2.28%，大于0的概率为97.72%。由表5可知，当湿度增加1个单位时，重特大事故发生的概率增加0.02%。其潜在原因为：湿度的增加会导致高速公路路面摩擦系数降低，车辆容易打滑，从而导致风险的上升。

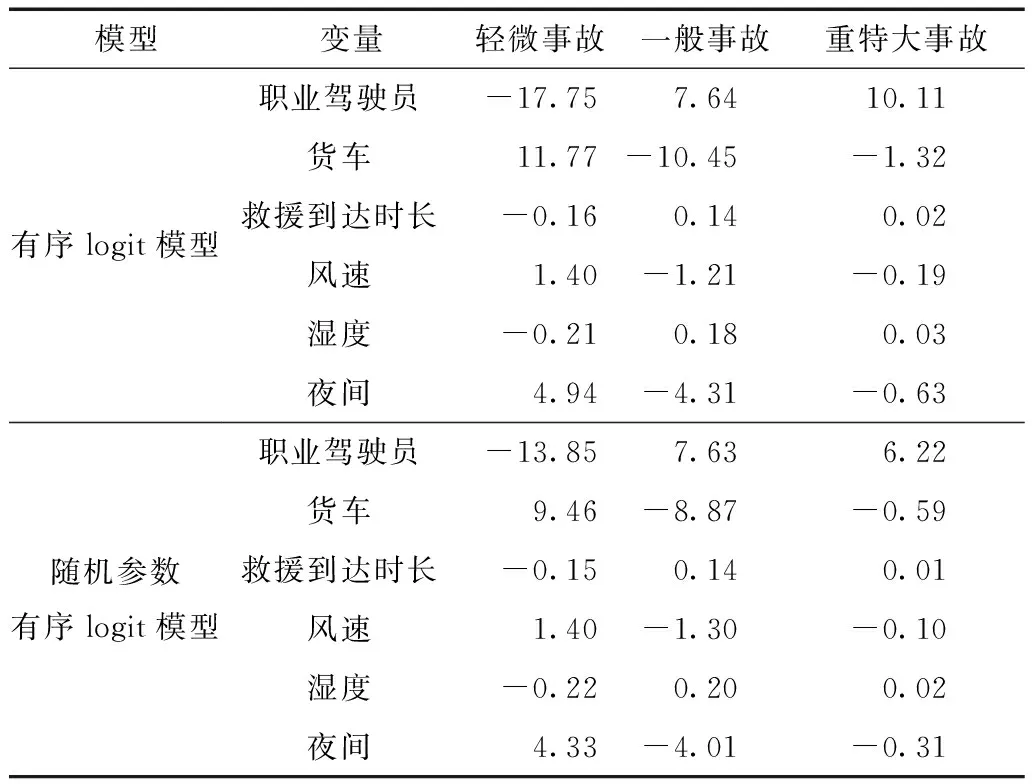
表5 边际效应Table 5 Marginal effect %

事故时间方面，相较于白天(早上六时至晚上六时)，若事故发生在夜间(晚上六时至第2天早上六时)，单车事故等级为轻微事故的概率提高4.33%，一般事故和重特大事故的概率分别降低4.01%和0.31%。潜在原因为：由于夜间光线较暗，驾驶员在夜间驾驶时警惕性更高，驾驶更为谨慎，从而降低了发生严重事故的风险。

4 结论

以高速公路单车事故等级为因变量，将事故等级划分为轻微事故、一般事故和重特大事故3个等级，并从人、车、环境和救援等方面选择了11个自变量，分别建立了有序logit模型和随机参数有序logit模型，得到如下结论。

(1)对数似然值、AIC和分类精度等评价指标的结果表明，随机参数有序logit模型比传统有序logit模型具有更优的数据拟合性能。

(2)肇事车主是否为职业驾驶员、肇事车辆是否为货车、救援到达时长、风速、湿度和事故发生时间是否为夜间对单车事故等级具有显著影响。其中，肇事车辆是否为货车和湿度对单车事故等级的影响存在显著的异质性。这些因素的边际效应表明：相比于非职业驾驶员，职业驾驶员发生重特大事故的概率更高；救援到达时长和湿度的增加以及风速的减小，将提高重特大事故的发生概率；相比于客运车辆等，货车发生重特大事故的概率更低；相比于白天，夜间发生重特大事故的概率更低。

(3)结合本研究的结果，提出以下安全改善措施：交管部门和运输企业需加强对职业驾驶员进行关于驾驶安全的教育，提高该群体对疲劳驾驶的警惕性；加强对高速公路的监控，及时识别事故的发生；优化事故救援流程，缩短事故救援到达时长；遇到湿度较大的天气时，高速公路管理部门及导航平台应在电子信息板和手机导航软件上发布相关消息，提醒驾驶员注意行车安全等。