引入时空特征的高速公路行程时间预测方法
林培群 夏雨 周楚昊
(华南理工大学 土木与交通学院,广东 广州 510640)
近年来,出行需求和汽车保有量的持续增长导致高速公路交通供需矛盾日益突出。准确地预测行程时间可为道路管制和出行决策提供信息依据,因此,在基础数据资源日益丰富、深度学习等技术快速发展的背景下,研究高速公路行程时间预测方法具有显著的理论和应用价值。目前,高德、百度等导航软件所提供的行程时间基于路段自身的历史和现状数据,未考虑交通网络的时空关联性。大量研究和工程实践表明,路段未来时刻的交通流不仅与过去时刻的数据具有关联性,周围路段交通流的变化同样会对其产生影响,因此在行程时间预测时引入时空特征具有必要性。
目前交通流时间序列预测模型主要分为自回归滑动平均模型、机器学习模型和神经网络模型。自回归滑动平均模型(ARMA)及其扩展模型差分整合移动平均自回归模型(ARIMA)[1- 2]都需进行数据平稳性检验,在大规模的数据及输入特征的情况下,这些模型难以良好拟合。机器学习模型中,常用的交通流预测模型有随机森林(RF)、极端梯度提升(XGBoost)、K-最近邻(KNN)、支持向量机回归(SVR)。Guy等[3]、Hamner[4]采用RF模型对交通量进行了预测,取得了较好的效果。Makoto等[5]、Yi等[6]采用XGBoost模型对交通量进行了预测,结果表明该模型预测精度较高且能够提高计算效率。王翔等[7]、陈娇娜等[8]采用KNN对道路平均行程时间进行了预测。傅成红等[9]构建改进的DL-SVR模型对交通量进行了预测,并与未改进的SVR模型及BP神经网络模型进行对比,结果表明DL-SVR模型的预测精度更高。Sun等[10]、Wang等[11]采用SVR模型对短时交通速度进行了预测,取得了较好的效果。长短时记忆神经网络模型(LSTM)是一种被广泛用于时序预测的神经网络模型。Tian等[12]、 Zhao等[13]采用LSTM模型对交通量进行了预测。在引入时空特征方面,现有研究主要在神经网络中引入Seq2Seq机制[14]和注意力机制[15- 16]。这些机制的引入对于探讨输入特征和输出目标的时空关联性具有一定作用,但引入过程较为复杂,如果是为了达到较好的预测效果,只需引入空间关联特征即可[17]。
综上所述,机器学习模型已被广泛运用于交通流的预测,但这些方法仍有不足:一是多数研究没有考虑空间特征,没有对路网多个出入口的动态特性进行综合考虑,仅将过去一定时间范围内的数据作为输入;二是输出结构单一,多数方法每次仅预测未来一个时刻的值,且预测步长较短,这增加了模型参数存储的空间并且降低了模型的实时响应能力;三是仅以误差的数值作为评判标准,没有从峰值预测准确率、不同步长的预测效果稳定性等不同角度综合分析各模型的优劣;四是没有在相同的数据集下进行多模型的比较。因此,本研究基于高速收费数据,以目标路段平均行程时间历史数据、周围收费站输入交通量历史数据、星期天数和小时数等时间外部特征作为输入特征,分别采用RF、XGBoost、LSTM、KNN、SVR对目标路段的平均行程时间进行预测,并从平均误差、峰值预测准确率、不同预测步长下的预测效果稳定性等方面对5种模型的预测性能进行综合分析;最后,使用贝叶斯回归方法对5种模型的预测能力进行综合寻优,提出了一种基于融合模型的预测方法。
1 预测模型
1.1 路网时空数据
高速收费系统采集了大量实时高精度的收费数据,通过预处理和统计,可得到丰富的交通量和行程时间样本,从而为高速公路交通流预测提供数据支撑。本研究使用广东省高速收费数据,每一行数据记录一辆机动车的行驶信息,包括车型、车牌、入口位置、入口时间(精确到秒)、出口位置、出口时间(精确到秒)、行驶距离、行程车速等信息。本研究将目标路段关联收费站的输入交通量、目标路段的历史行程时间及星期天数、小时数、分钟数等时间外部特征作为输入,采用随机森林等算法对目标路段的行程时间进行预测。
分别用d、tu、tv、tp表示数据覆盖天数、统计单位时间、历史数据步长、预测步长,则输入样本数量Nin的计算公式为
(1)
此时,输入矩阵X和真实值矩阵Y可表示为:
X=(x(1),x(2),…,x(S))
(2)
Y=(y1,y2,…,yN)T
(3)
式中,x(S)表示第S个输入特征。则训练集可表示为
T=(X,Y)={(x1,y1),(x2,y2),…,(xN,yN)}
(4)
各模型的训练过程实质上是在训练集中找到从X到Y的最优映射,使预测值和真实值的误差最小,这种映射表示为
(5)
式中,φ表示从输入到输出的映射,T表示训练集。
1.2 方法框架
1.2.1 随机森林模型
随机森林(RF)是一种基于多个决策树的算法,其目的是找到一种最优的划分方式将输入空间划分为M个子集{R1,R2,…,Rm,…,RM},使每个子集中的样本都属于同一个类别[18- 19]。对于回归问题,一般采用卡特方法(CART)构建决策树,其关键是选出最优的特征x(s)和分割点q。在每个节点,决策树都将数据集Tq划分为两个更小的子集R1和R2:
R1(s,q)={x|x(s)≤q}
(6)
R2(s,q)={x|x(s)>q}
(7)
最优的特征x(s)和分割点p满足以下条件:
(8)
式中,xn和yn分别表示第n个样本的输入和输出值。c1和c2为子集的样本均值,计算方法为
(9)
决策树通过不断分割进行生长,直到树的深度达到预设的阈值,最后的输出表示为
(10)
式(10)中,Ind为指示函数,表示为
(11)
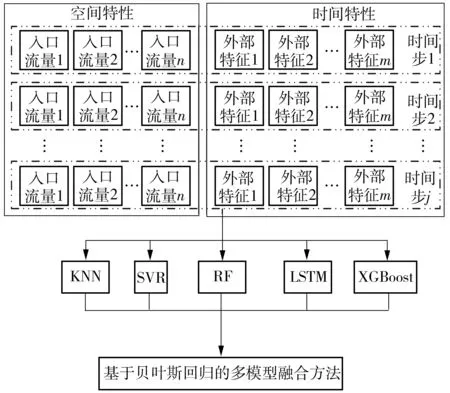
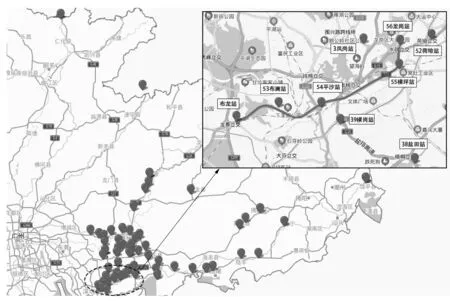
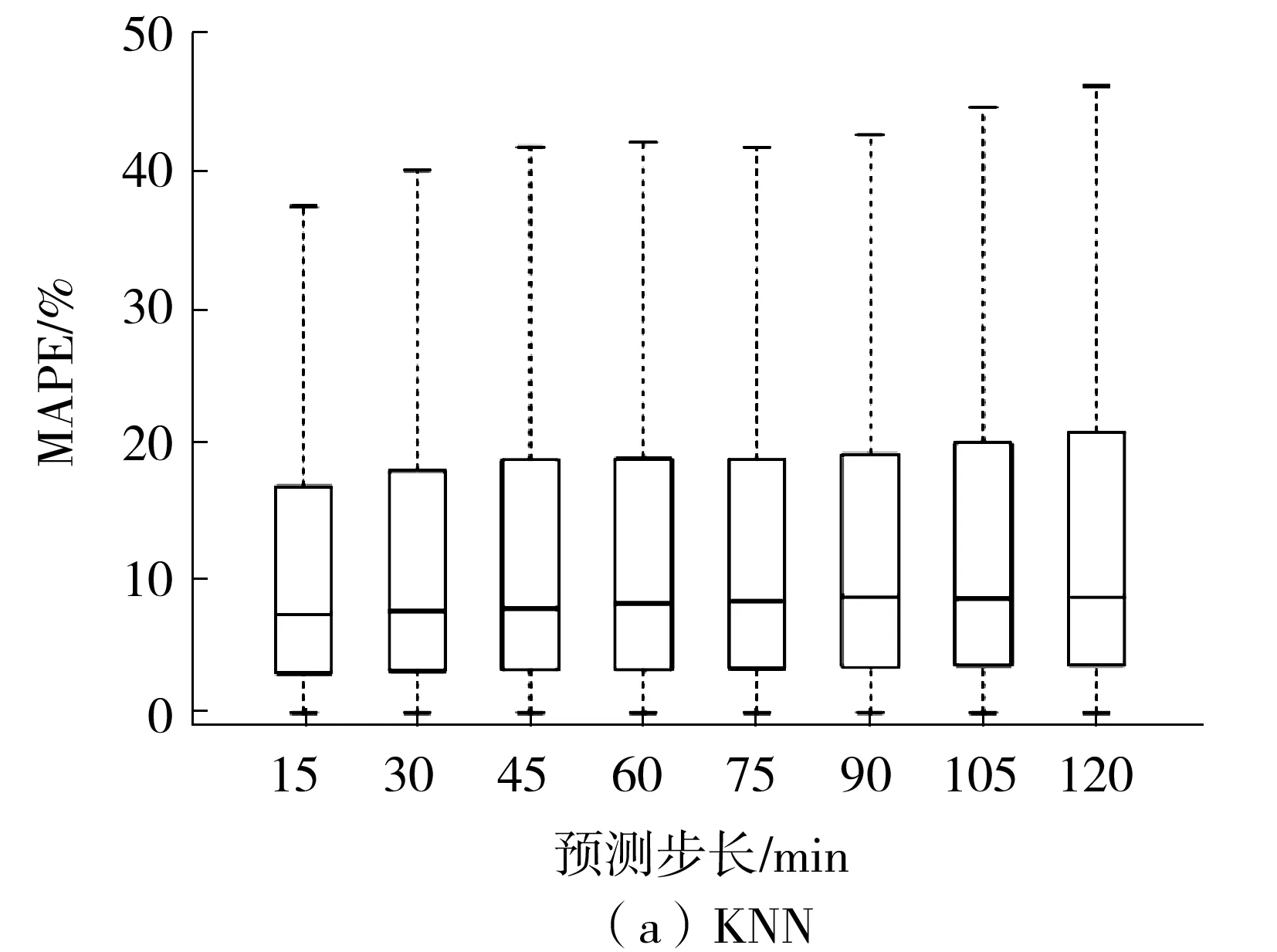
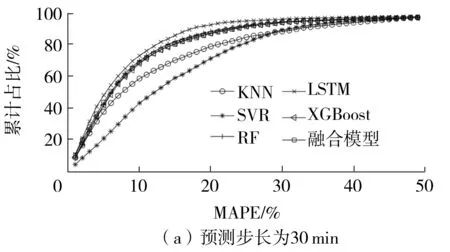
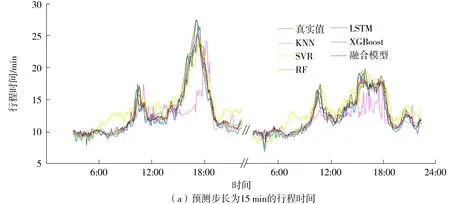
随机森林算法首先确定决策树的个数B。对于决策树b(b=1,2,…,B),从训练集T中抽取N个样本(bootstrap抽样,将样本放回后继续下次抽样)且随机选择Z个特征(Z (12) 训练时,随机森林算法可通过调整决策树的个数和最大深度来提高算法的拟合能力。 1.2.2 极端梯度提升模型 极端梯度提升(XGBoost)是一种基于梯度提升决策树的改进算法[6]。梯度提升决策树的输入输出映射可表示为 (13) 其中,G为决策树的个数,fg表示第g棵决策树。在每棵决策树中,分别用L和w表示叶子的个数和权值。梯度提升决策树的损失函数表示为 (14) 为避免过拟合,XGBoost在式(13)的基础上增加了正则项,其损失函数表示为 (15) 其中,Ω(fg)表示为 (16) 1.2.3 K-最近邻算法 K-最近邻(KNN)是一种基于距离的非参数算法[7]。对于测试集Ttest中的某个输入x0,KNN的核心思想是在训练集Ttrain中建立向量空间模型,基于距离的度量找到与x0最接近的K个点,用集合RK表示 RK={(x1,y1),(x2,y2),…,(xk,yk)…,(xK,yK)}T (17) 则x的输出可表示为K个输出值的平均值: (18) KNN有多种距离度量函数,其中最常用的是欧式距离,计算方法为 (19) 对于高维输入,常采用高斯核函数为K个近邻点赋值权重,计算方法为 (20) 训练时,可通过调整K值来提高KNN算法的拟合能力。 1.2.4 支持向量机回归模型 支持向量机回归(SVR)是支持向量机对回归问题的应用。支持向量机(SVM)的核心思想是找出一个使类间间隔最大化的超平面,SVR的原理与之类似[20]。在SVR中,从X到Y的映射表示为 (21) 式中,w表示输入的权值。 (22) 以偏差最小化为目标,建立如下优化问题以求解w和b: (23) 其中C是正则化常数,可避免过拟合问题。 1.2.5 长短时记忆神经网络 长短时记忆(LSTM)是为解决循环神经网络(RNN)的长期依赖问题而提出的一种循环神经网络,主要通过输入门、输出门、遗忘门及过渡记忆细胞来控制长记忆和短记忆的传递与输出[21]。对于第j个时间步的输入,数据首先经过遗忘门以清除无用信息,表示为 fgj=Sig(Wfg·[hj-1,xj]+bfg) (24) 式中,fgj表示第j个时间步的遗忘门,Wfg和bfg分别表示遗忘门的权值和偏置,hj-1表示第j-1个时间步的隐藏状态,xj表示第j个时间步的输入,Sig(·)表示Sigmoid激活函数。 其次,输入门和过渡记忆细胞决定细胞状态存储的新信息,表示为: ipj=Sig(Wip·[hj-1,xj]+bip) (25) (26) (27) 最后,由输出门输出隐藏状态和预测值,表示为 opj=Sig(Wop·[hj-1,xt]+bop) (28) hj=opj×tanh(Cj) (29) (30) 式(28)中,opj表示第j个时间步的输出门,Wop和bop分别表示输出门的权值和偏置。式(30)中,Wh和bh分别表示隐藏层的权重和偏置。 以真实值和预测值的误差最小化为目标,可建立如下目标函数: (31) LSTM的训练过程实质上是通过误差的反向传播,不断调整权重和偏置,使预测值不断接近真实值。 1.2.6 贝叶斯回归模型 贝叶斯回归(BLR)是一种使用贝叶斯推断方法求解的回归模型,贝叶斯回归以模型中的参数作为随机变量,通过训练来确定参数的后验分布概率[22]。贝叶斯回归模型可表示为: f(x)=wTx (32) (33) 式(32)中,w表示输入的权值。式(33)中,η为符合正态分布的高斯噪音,即η~Nor(0,σ2)。贝叶斯回归分为推断和预测两个部分,贝叶斯推断表示为 pro(W|X,Y)∝pro(Y|W,X)pro(W) (34) pro(Y|W,X)~Nor(WTxi,σ2)、对W的先验假设pro(W)~Nor(0,Σ)都为高斯分布,则pro(W|X,Y)也为高斯分布且pro(W|X,Y)~Nor(μw,Σw),其中: μw=σ-2Σ-1XTY (35) Σw=Σ-1 (36) 式中,μw和Σw分别表示高斯分布的均值和方差。 已知μw和Σw,则可进行预测。对于测试样本(x*,y*),有 f(x*)=x*TW~Nor(x*Tμw,x*TΣwx*) (37) (38) 即预测输出也是一个高斯分布。 本研究提出一种基于贝叶斯回归的多模型融合预测方法,该预测方法的框架如图1所示。 图1 基于贝叶斯回归的多模型融合预测方法框架 评估预测精度的指标有平均绝对误差(MAE)[8]、平均绝对百分比误差(MAPE)[8]和均方误差(MSE)[11]。 平均绝对误差避免了误差正负相消的情况,能更好地反映预测误差的实际情况,其计算公式为 (39) 相对误差是绝对误差与真实值的比值,用于反映不同测量结果的可靠程度,其计算公式为 (40) 均方误差可综合反映预测值与真实值的差异程度,其计算公式为 (41) 收费数据包含从目标收费站驶出的车辆的入口收费站信息,这些收费站都可作为目标收费站的关联站点。如图2所示,本研究以广东水官高速龙岗—布龙段为对象,龙岗收费站和布龙收费站都位于深圳市龙岗区,路段里程为19.8 km。选取该路段起讫点(OD)收费站及关联的65个收费站2019年7月1日至9月30日的收费数据,统计全天00:00—23:59的数据,以tu=5 min为时间间隔,计算平均行程时间。实验中各模型都采用多个步长同时输出的预测模式,输入步长为tv=12,预测步长范围为2 h,每个步长间隔15 min。实验中,对KNN模型、SVR模型、RF模型、LSTM模型和XGBoost模型采用相同的输入,Bayesian模型的输入是前5种模型的输出结果。在数据集划分上,将前76天(2019年7月1日至2019年9月14日)共21 888组数据作为训练样本,将后16天(2019年9月15日至2019年9月30日)共4 320组数据作为测试样本。由于预测步长影响测试样本覆盖范围,为更准确地比较各模型的预测性能,计算平均误差时,仅统计每天3:05—22:10的数据。 图2 路网站点位置Fig.2 Location of road network toll stations Pearson相关系数用于测量两个变量之间的相关性,其范围介于-1和1之间,越靠近1代表相关性越强,在引入空间特征的交通流预测研究中,通常采用Pearson相关系数(PCCs)衡量输入特征与输出的空间相关性。图3示出了各站点的输入流量与预测输出即目标路段的行程时间之间的Pearson相关系数。 图3 各站点输入流量与预测输出(行程时间)的Pearson相关系数Fig.3 Pearson correlation coefficient between the input flow of each station and the output(travel time) 在机器学习算法中,随机森林和LSTM等模型在训练时会自动探索各输入特征和输出的相关性,并赋予相应的权重。图4分别示出了RF模型和LSTM模型的输入特征的权值分布。由于Pearson相关系数主要用于衡量线性相关性,而RF模型和LSTM模型都是非线性算法,对于相同的输入特征,Pearson相关系数与RF模型、LSTM模型的权值分布有所差异,且由于算法结构的差异,两种模型对相同输入特征赋予的权值分布也有所不同。 不同预测步长下各模型的误差如表1、表2、表3所示。从表中可以看出:各模型的预测误差都随着预测步长的增加而增加,各步长下RF模型、XGBoost模型和融合模型的误差要低于KNN和SVR模型;而LSTM模型在步长较短的情况下的预测效果最好,但随着步长的增加,其预测精度明显下降,预测误差显著高于RF模型、XGBoost模型和融合模型。 表1 不同模型的均方误差计算表Table 1 Calculation table of mean square error of different models 表2 不同模型的平均绝对误差计算表Table 2 Calculation table of average absolute error of different models 表3 不同模型的平均绝对百分比误差计算表Table 3 Calculation table of average absolute percentage error of different models % 为进一步对比分析5种模型的预测效果,采用箱型图和累计分布函数(CDF)对预测误差进行展示。从图5可以看出,各模型的MAPE的中位数和上四分位数都随着预测步长的增加而小幅增加,除了SVR模型,其他模型的最大上四分位数都低于25%,SVR模型的最大上四分位数也低于30%。这表明不同步长下各模型的预测性能具有稳定性。LSTM模型的最大MAPE随着预测步长的增加而呈现明显上升趋势,这表明步长对LSTM模型的预测能力有着显著的影响。图6的CDF曲线示出了相同步长下各模型的误差累计分布情况。曲线上某点的横坐标表示MAPE的取值,纵坐标表示MAPE低于该点横坐标的样本数占比。可以看出,相同步长下融合模型、RF模型和XGBoost模型的表现要优于KNN模型和SVR模型,而LSTM模型在步长较短的情况下表现最优,但随着步长的增加,LSTM模型的预测效果显著变差。 图5 不同预测步长下各模型的预测误差箱型图 图6 相同预测步长下各模型的CDF曲线 峰值样本的预测误差也是评判模型预测能力的重要指标。为分析各模型对峰值的预测能力,本研究选取了两天峰值明显变化的数据,对15 min和30 min两种步长下各模型的预测误差进行了可视化,所得结果如图7所示。从图中可以看出,不同步下KNN模型对峰值的预测误差较大;SVR模型对峰值的预测误差要小于KNN模型,但在平峰时段却出现预测误差变大的现象;融合模型、RF模型、XGBoost模型和LSTM模型对峰值的预测能力较好,在步长较短时,LSTM模型对峰值的预测能力最好。 图7 绝对百分比误差热力图Fig.7 Heatmap of absolute percentage error 综上所述,预测步长较短时,可选择RF模型、XGBoost模型、LSTM模型、基于贝叶斯回归的融合模型进行预测;预测步长较长时,可选择RF模型、XGBoost模型和基于贝叶斯回归的融合模型进行预测。 各模型的训练时长及每秒预测样本数见表4,其中LSTM模型执行了300轮训练。训练时,KNN模型仅构建快速查找结构,其他模型都进行参数存储,但融合模型的输入较少,因此KNN模型和融合模型训练时长较短。预测时,SVR模型和KNN模型需在训练集中计算或查找相似样本,因此预测执行时间较长,每秒预测样本个数较少。 本研究使用KNN模型、SVR模型、RF模型、LSTM模型、XGBoost模型和基于贝叶斯回归的融合模型对引入时空特征的高速公路平均行程时间进行了多步长同时输出的预测,结果表明: (1)5种模型的预测误差都随着预测步长的增加而增加,但MAPE的中位数和上四分位数增加幅度较小; (2)不同步长下,融合模型、RF模型和XGBoost模型的预测效果优于KNN模型和SVR模型;步长较短时,LSTM模型预测性能优越,但随着步长的增加,其预测性能明显下降; (3)基于贝叶斯回归的融合模型可自动调整权重,综合各模型的优点以保持较好的预测效果,克服了单一预测方法的局限性。 (4)RF模型、LSTM模型训练时长较长但每秒预测样本数较大,对比之下,SVR模型、KNN模型训练时长较短但每秒预测样本数较小;XGBoost模型和融合模型训练时长短于RF模型和LSTM模型,每秒预测样本数大于SVR模型和KNN模型。 结合交通拥堵问题,下一步研究将针对节假日的高速公路平均行程时间展开预测。


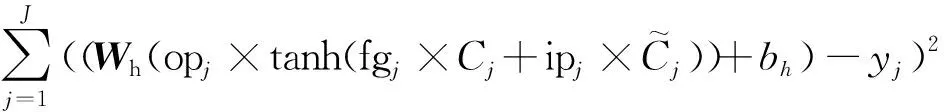

1.3 模型预测性能验证指标
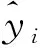
2 实验结果与分析
2.1 输入特征分析

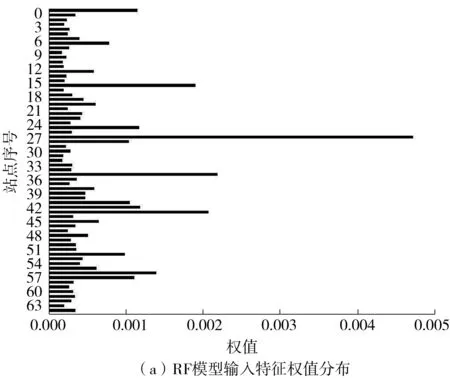
2.2 预测精度分析



2.3 执行时长分析
3 结论

