基于转角的简支梁初始抗弯刚度识别方法

杨雨厚 杨绿峰 覃炳贤 郝天之,3

(1.广西大学 土木建筑工程学院,广西 南宁 530004;2.广西北部湾投资集团有限公司,广西 南宁 530029;3.广西交科集团有限公司,广西 南宁 530007)

抗弯刚度是梁结构性能及损伤状况评价的最主要指标[1- 2],但该指标在梁成型后的实际分布是不确定和随机的[3]。而获得梁体当前实际抗弯刚度值具有重要工程意义:一是可据此发现梁体是否存在初始缺陷,初始缺陷是运营期桥梁病害产生的内因,在役桥梁病害一般由初始缺陷发展而来[4];二是可为后期结构损伤识别和健康监测提供“原始指纹”,解决当前常采用理论设计状态作为初始状态而与实际不相符的问题[5]。

目前,在结构抗弯刚度识别领域已有不少研究成果。按输入数据的不同,通常可分为静力和动力识别两大类[6- 7]。两者在处理方法上有共同之处,即均以结构响应的误差最小为目标,进行最优化求解的结构特性输出反演[5- 8]。以振动模态为核心的动力识别技术[9- 11]具有测试快捷、可不中断交通的优点,一直是国内外研究热点,但其存在对结构局部损伤不敏感且易于受环境温度等测量噪声影响的不足,在工程实践中的应用不能尽如人意[12- 13]。静力识别方法[14- 16]虽不能在线进行,但方法比较直观,结果稳定可靠,且只要试验条件较好,就可保证位移或应变的测试精度,容易被工程师接受,是获得结构真实抗弯刚度的重要途径,也是目前结构状态评估普遍使用的方法。然而,现有根据实测的静态响应反演获得结构刚度信息的方法一般存在这样的缺点[5]:优化方法需配合有限元模型(求理论值),相互之间需不断的调用,增加了识别问题的复杂性和工程应用的难度;且优化算法选择不当时,容易使结果陷入局部极小值;另外,优化变量对噪声敏感,计算中可能会出现相互矛盾的优化方程,造成求解困难。

为此,针对简支梁具有静力加载方便、易于测试且测试结果可靠等特点,本研究采用静力加载的方式,测试(或间接得到)简支梁在分段截面处的转角值,通过转角与分段梁体抗弯刚度之间的关系式,反向求解出各段梁体抗弯刚度值,以达到简支梁抗弯刚度的识别。随后,利用数值模拟方法和试验数据验证了本研究提出的识别方法的可靠性。在此基础上,通过矩阵条件数分别分析了梁体分段数量、作用力大小、类型、个数及作用位置共5个因素对识别方程组稳定性的影响规律。最后,在理论计算转角上叠加随机误差,考察了所提识别方法的鲁棒性。相关研究不仅可用于简支梁静载试验评估及质量鉴定,而且还可为既有梁结构的刚度退化评估及损伤识别提供参考方法。

1 理论推导

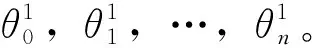
为求解,先做以下假设:

(1)已知荷载作用下梁体变形属于小变形;

(2)分段内梁体抗弯刚度相等;

(3)分段内梁体局部损伤等效为该梁段整体抗弯刚度的降低。

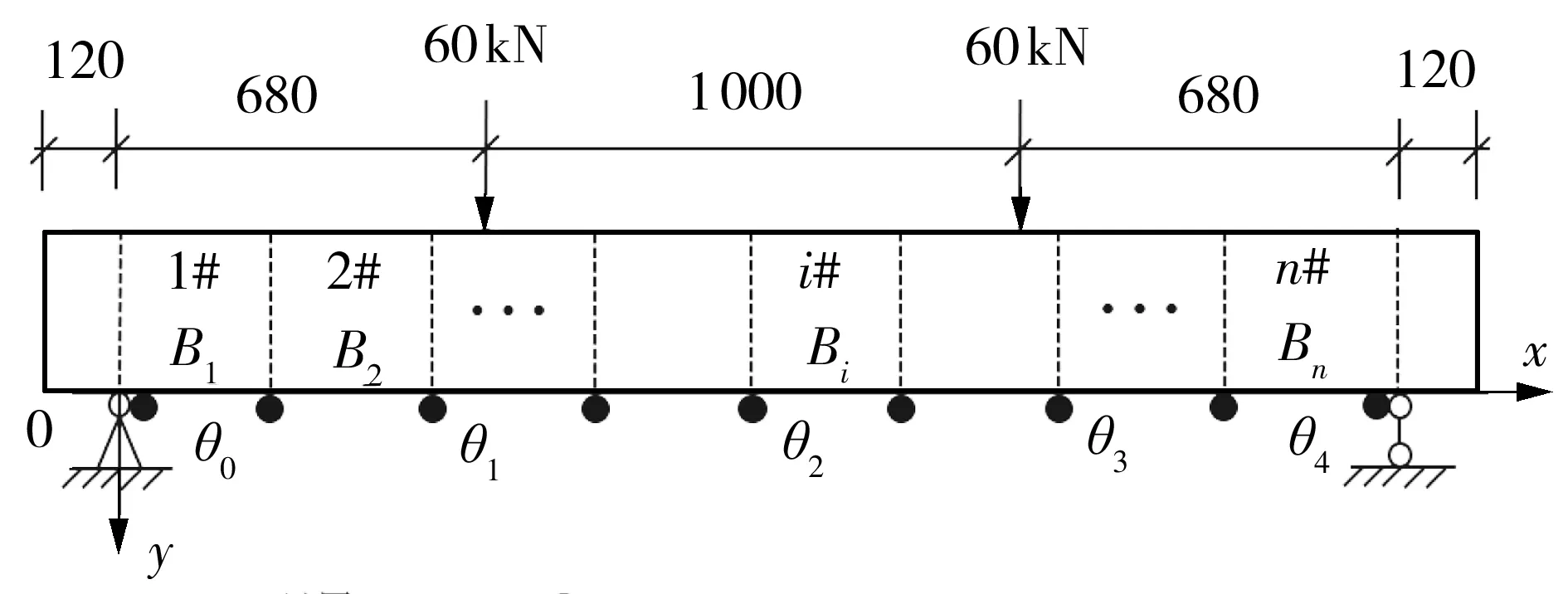
图1 典型简支梁受力结构示意图Fig.1 Schematic diagram of typical simply supported beam

过程中需利用广义奇异函数[17]S(x),该函数表达式为

S(x)=〈x-a〉n

(1)

式中,〈·〉符号为麦考利括号,x为未知变量,a为常数,n为次幂。

下面推导中主要用到广义奇异函数(n≥1)与Heaviside函数乘积的积分，该积分满足下列关系:

(2)

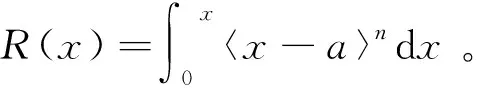
对于图1所示梁构件的抗弯刚度B(x),用广义奇异函数可表示为

(k3-k2)〈x-x2〉0+…+(ki+1-ki)·

〈x-xi〉0+…+(kn-kn-1)〈x-xn-1〉0]

(3)

式中,k2、k3、ki、ki+1、kn-1、kn为1#梁体分别与2#段、3#段、i#段、(i+1)#段、(n-1)#段和n#段梁体抗弯刚度的比值,x1、x2、xi和xn-1分别表示1#段、2#段、i#段和(n-1)#段梁体右侧节点的坐标值。

由Timoshenko梁理论,在单位力作用下考虑剪切变形影响时梁的基本微分方程[18]为

(4)

(5)

式中,y为梁的挠度,φ为梁的转角,C(x)为梁的剪切刚度,B(x)为梁的抗弯刚度,q(x)为作用在梁上的载荷密度函数。

由图1可见,作用在梁上单位力的密度函数用广义奇异函数可表示为

q(x)=〈x-z〉-1-(1-m)〈x-0〉-1-m〈x-l〉-1

(6)

式中,m=z/l。

将式(6)代入式(4),并对x进行积分得

(1-m)〈x-0〉0-m〈x-l〉0

(7)

将式(7)代入式(5),并对x进行积分得

(1-m)〈x-0〉-m〈x-l〉

(8)

式中,Q0、M0均为积分产生的常数项,由图1易知,Q0=0、M0=0。

饲料的化学处理方式主要有碱化处理(氢氧化钠、氢氧化钙等)，氨化处理(尿素等)和将前两种方法结合的复合化学处理。碱化处理是指利用碱性物质破坏细胞壁中结构性碳水化合物和木质素之间连接的酯键[25]，增加纤维素之间的空隙度，增大瘤胃微生物附着量，提高纤维素的降解率，改善细胞壁的消化[26]。氨化处理是指饲料与氨作用时，有机物质与氨会发生氨解反应，从而打断木质素与多糖之间的酯键，在提高饲料利用率的同时形成氨盐，氨盐可作为瘤胃微生物的氮源。

对式(8)进行积分可得该梁在单位力作用于z处时x截面的转角方程φ(x,z):

G(xi,z)〈x-xi-1〉0]

(9)

假设某一简支梁上作用有m个集中力和r个均布力,zj处集中力大小为Fj(1≤j≤m),hw至gw范围作用的均布力大小为qw(1≤w≤r)。此时,测试梁体两端支点截面处的转角分别为θ0和θn,分段截面处的转角分别为θ1、θ2、…、θi。理论转角应与实测转角相等,由此建立下列方程组:

(10)

经整理,式(10)可用矩阵方式表示为

An×nK1×n=θ1×n

(11)

(12)

则

(13)

式中,M(x)为荷载作用下等效的等截面梁弯矩,Bse为等效的等截面梁抗弯刚度,M1(x)、M2(x)、Mn(x)分别为荷载作用下实际梁1#段、2#段和n#段的梁体弯矩。

2 识别方法的有限元数值和试验验证

2.1 有限元数值方法验证

某C30混凝土简支梁,矩形截面,宽×高=0.15 m×0.30 m,梁长2.6 m,计算跨径2.36 m。基于“虚拟分割”思想,将该梁按计算跨径四等分。在距离跨中截面两侧各0.5 m位置分别施加60 kN集中力,通过弹性有限元方法计算此时梁支点及四分点截面处的转角值。结构受力见图2。为验证不同情况,特设置不同的损伤工况,详见表1。

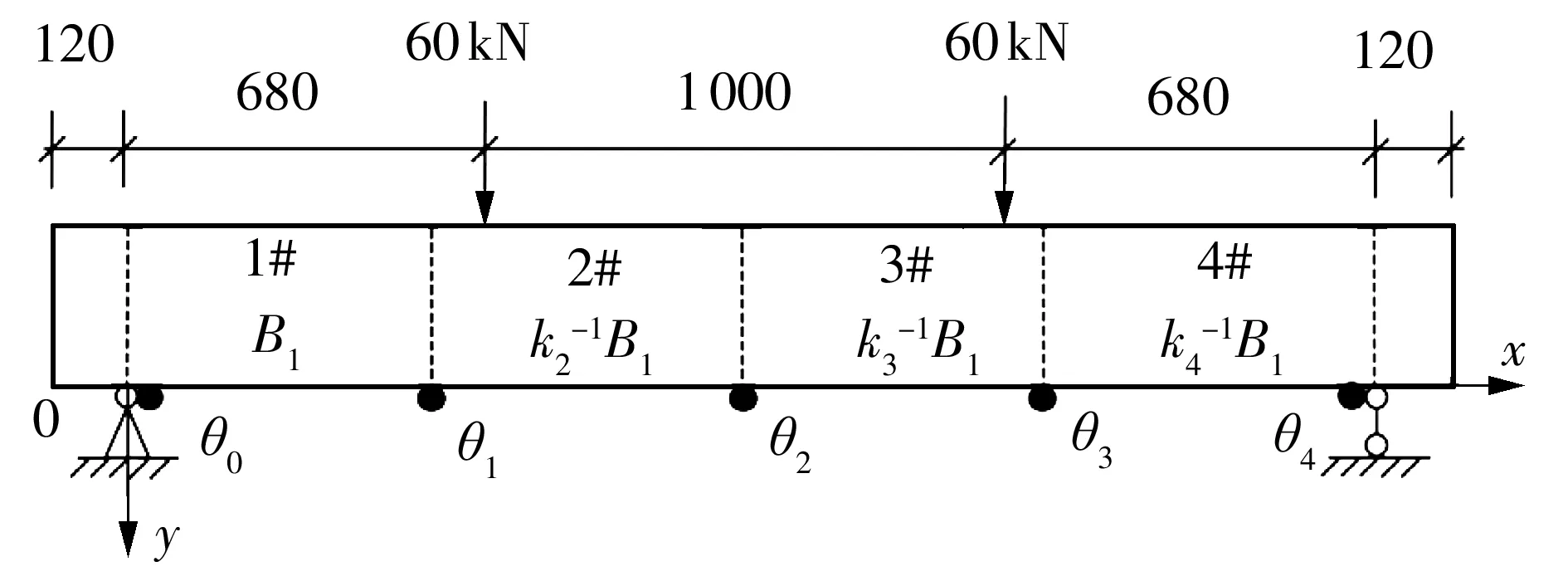
图2 有限元方法的结构受力图(单位:mm)Fig.2 Structure diagram of finite element method(Unit:mm)

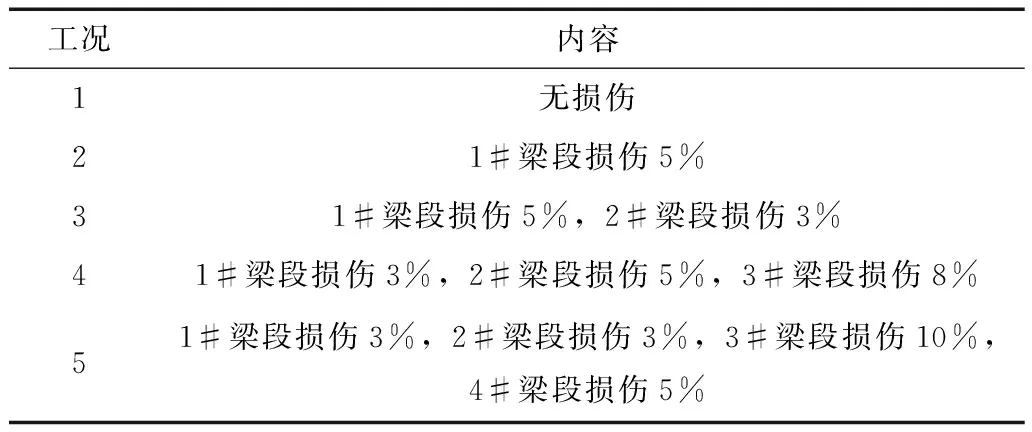
表1 工况设置表(有限元方法)1)Table 1 Working condition setting table(finite element method)

1)通过抗弯刚度的折减模拟损伤;因初始损伤一般不大,故将损伤值均设置在较小范围。

以工况1为例,将用有限元方法计算得到的转角值代入式(11),可得

(14)

式(14)中各数据是在力的单位取kN,长度单位取m,转角单位取rad的前提下得到的。值得说明的是此时转角直接取有限元计算值,并未考虑测量误差影响,因为该部分将在后面专门论述。通过式(14)可求解得到各梁段抗弯刚度值。类似地,也可得到其他工况识别结果，均列于图3。

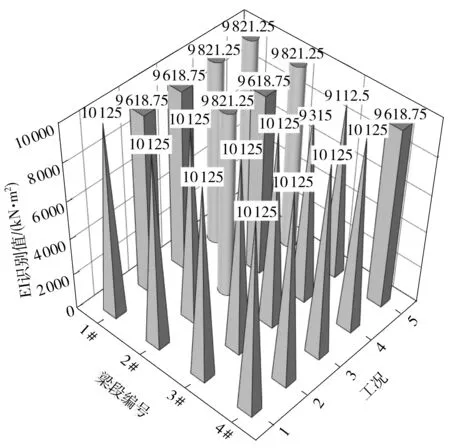
图3 各工况下的抗弯刚度识别值

由图3及表1可知,在不同损伤工况下,采用本方法识别出的抗弯刚度值与事先设定值最大相对误差绝对值为0.12%。弹性有限元理论验证结果表明，本研究提出的方法是有效的,在不考虑测量误差情况下具有非常高的识别精度。

2.2 试验验证

采用文献[19]的简支梁损伤识别试验中工况2的测试数据。该工况下加载的集中力为30 kN,测试得到此时梁计算跨径八分点处的实测挠度值,详见该文献中的表2。利用二阶中心差分法,将挠度值转换为转角值,结果列于本文表2。

将表2中转角值代入式(11),可计算得到每段梁体的抗弯刚度识别值,结果见图4。图中,抗弯刚度EI理论值为试验梁混凝土弹性模量与截面惯性矩的乘积;损伤量为EI识别值与理论值之差与理论值的比值,为负则说明识别的该梁段实际抗弯刚度小于理论值,亦表明该段梁体存在缺陷。

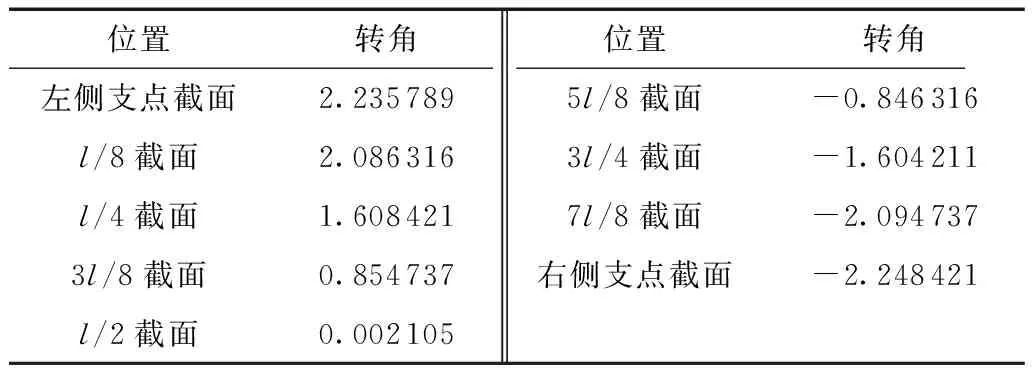
表2 转角值Table 2 Rotation angle 10-3 rad

由图4可知,识别出的2#-7#梁段实际抗弯刚度小于理论值,说明在加载过程中这些梁段出现了不同程度裂缝,导致其抗弯刚度的降低,且越靠近跨中截面损伤量越大,说明开裂的程度越严重,这与文献[19]的试验结果相吻合。另外,识别出的1#段和8#段梁体抗弯刚度接近于理论值,这说明这两段梁体在加载过程中未出现开裂,同时也验证了本方法的可靠性。

图4 抗弯刚度EI理论值与识别值对比

将识别出的每段梁体抗弯刚度代入式(13),求得此工况下整个简支梁的等效抗弯刚度，为4 438.269 kN·m2。把识别出的各梁段抗弯刚度值及等效抗弯刚度分别输入到有限元模型中,计算得到试验梁计算跨径八分点的计算挠度值,并与实测挠度值进行对比分析,结果见图5。由图5可知,采用本研究提出的方法识别得到的试验梁各段实际抗弯刚度及等效抗弯刚度计算出的结构挠度与实测挠度均能较好吻合,与实测挠度最大相对误差绝对值为3.2%,进一步验证了本方法的可靠性。

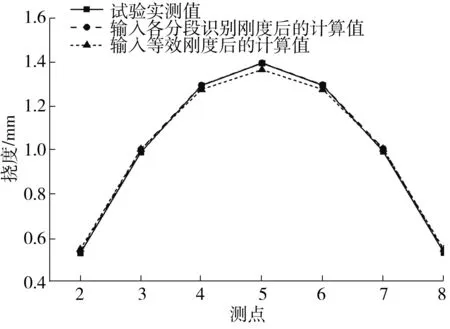
图5 挠度测试值与计算值对比

3 识别方程组的稳定性分析

根据所建立线性方程组系数矩阵的条件数Cond2(A)对识别方程组的稳定性进行分析。由式(10)可知,矩阵条件数与梁体分段数量(因素1)、作用力大小(因素2)、作用力类型(因素3)、作用力个数(因素4)、作用力作用位置(因素5)这5个因素有关。在第2.1节的有限元模型基础上,改变以上影响因素值,研究矩阵条件数的变化规律。各影响因素下工况设置及相应矩阵条件数的计算结果分别见图6-图15。

由图6和图7可知,分段数量越多,矩阵条件数Cond2(A)越大,且Cond2(A)与分段数量n近似满足各项系数均为正的一元二次方程曲线关系,可见Cond2(A)与n的平方相关，其影响非常显著。由图8和图9可知,对于两个相同的集中力,不管力的大小为何值,Cond2(A)总是相等的。两个力不等时,存在一个最优的组合,可使Cond2(A)最小。但总体而言,荷载大小对Cond2(A)的影响非常小,可不考虑。然而从测试转角值的角度考虑,荷载越大测试转角值越大,越有利于测量相对误差的控制。由图10和图11可知,不管采用集中力还是均布力,Cond2(A)基本不变,其对识别方程稳定性的影响可忽略。由图12和图13可知,荷载数量越多，Cond2(A)越小,其对Cond2(A)的影响相对较显著。由图14和图15可知:单个集中力时,Cond2(A)随着力从起点(即作为基准的1#段梁体)到梁跨中逐渐减小,然后基本保持小幅度的波动;当为2个集中力时,两者之间距离越大,即力越分散,Cond2(A)越小;当为3个集中力时,亦表现出力越分散Cond2(A)越小的规律。若集中施加3个集中力,则加载在梁跨中附近比施加在端部附近的Cond2(A)更小。

工况1：n=2 工况5：n=10工况2：n=4 工况6：n=12工况3：n=6 工况7：n=14工况4：n=8 工况8：n=16

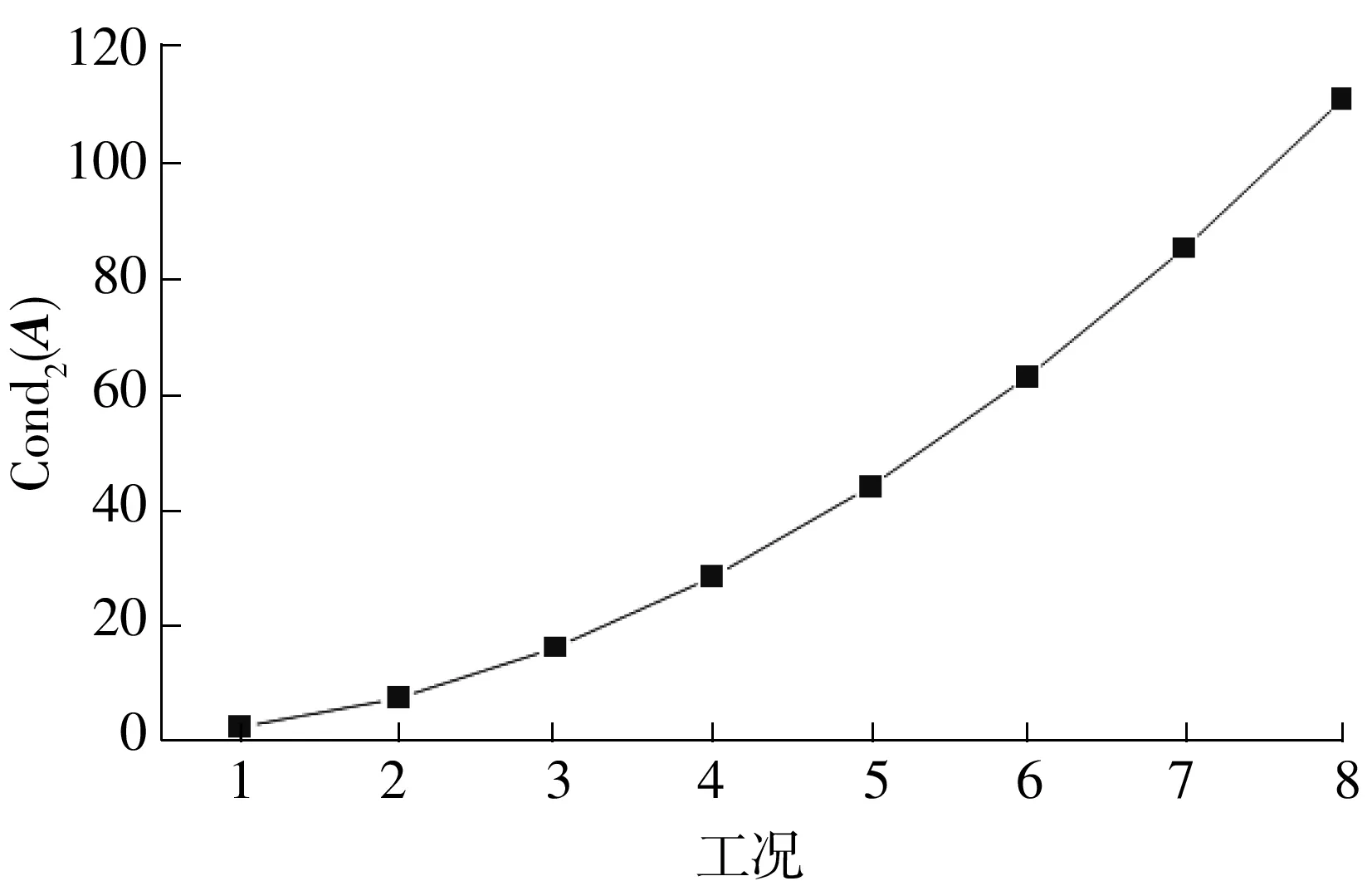
图7 因素1的矩阵条件数Fig.7 Matrix condition number of factor 1

工况1：p1=p2=40 kN 工况5：p1=40 kN，p2=60 kN工况2：p1=p2=60 kN 工况6：p1=40 kN，p2=80 kN工况3：p1=p2=80 kN 工况7：p1=40 kN，p2=105 kN工况4：p1=40 kN，p2=28 kN 工况8：p1=40 kN，p2=130 kN

图9 因素2的矩阵条件数Fig.9 Matrix condition number of factor 2

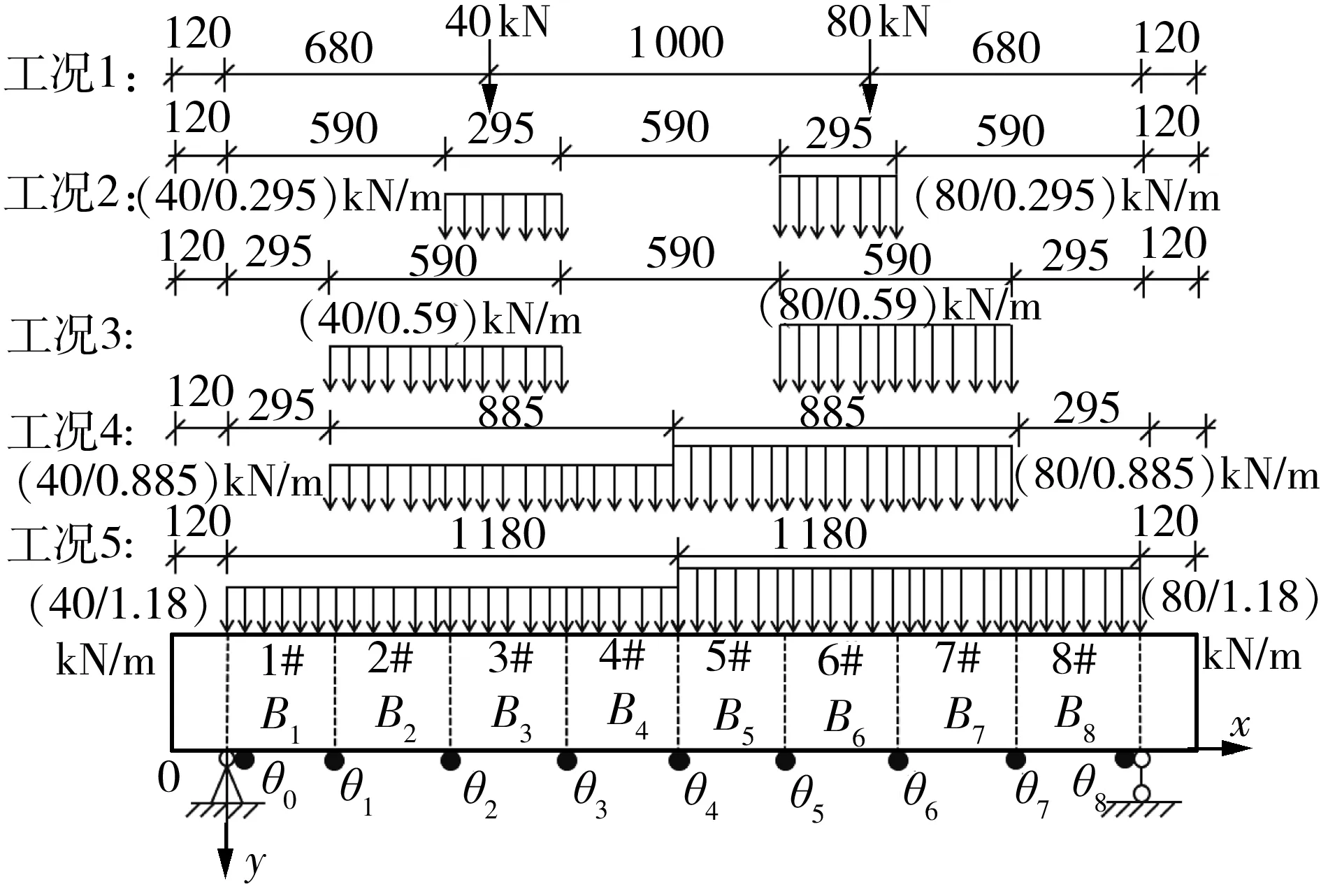
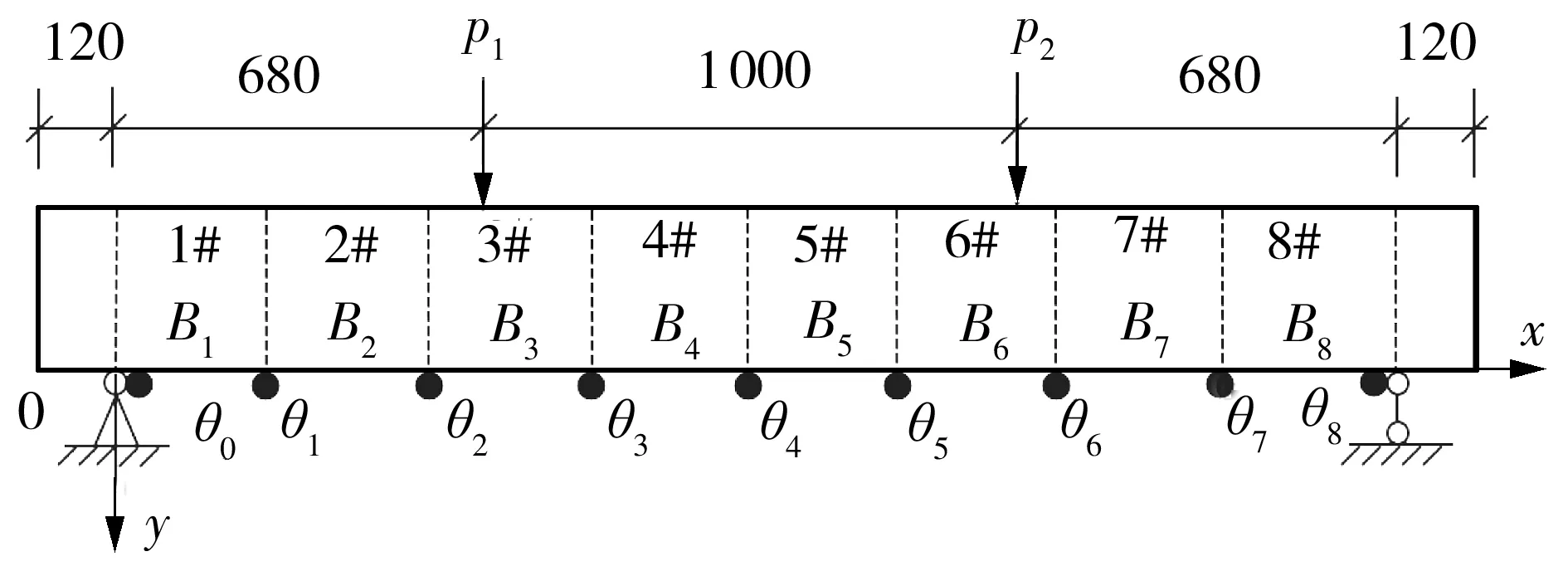
图10 因素3的工况设置(单位:mm) Fig.10 Working condition of factor 3(Unit:mm)

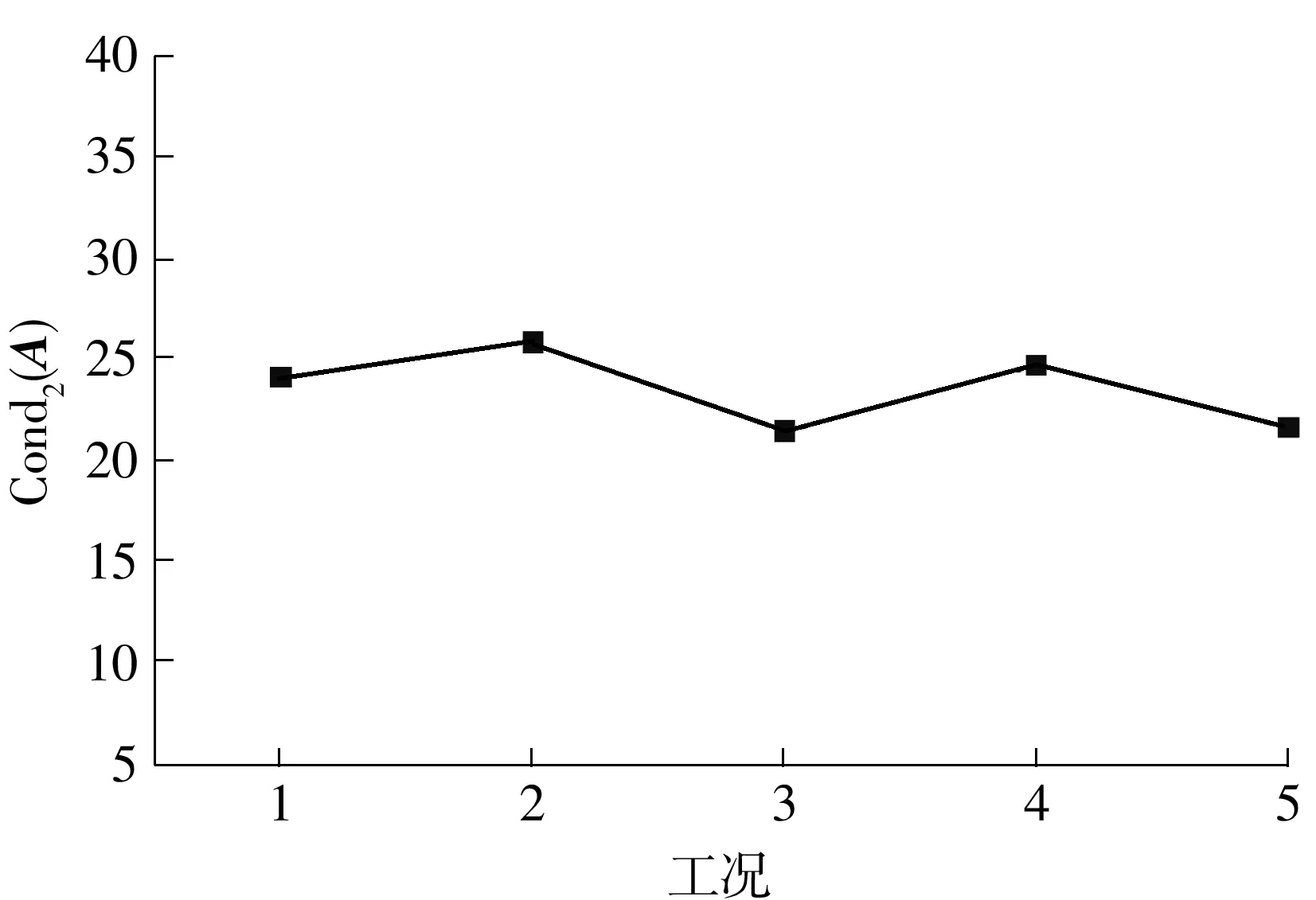
图11 因素3的矩阵条件数Fig.11 Matrix condition number of factor 3

图12 因素4的工况设置(单位:mm)Fig.12 Working condition of factor 4(Unit:mm)

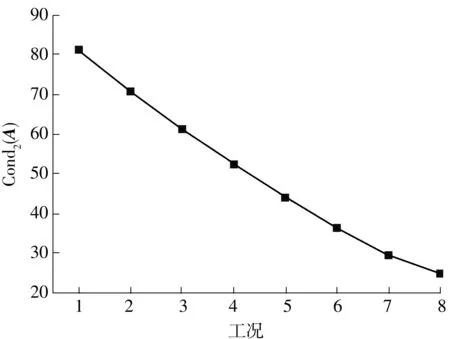
图13 因素4的矩阵条件数Fig.13 Matrix condition number of factor 4

工况1：x1=1×147.5 mm工况2：x1=2×147.5 mm ⋮ ⋮工况15：x1=15×147.5 mm

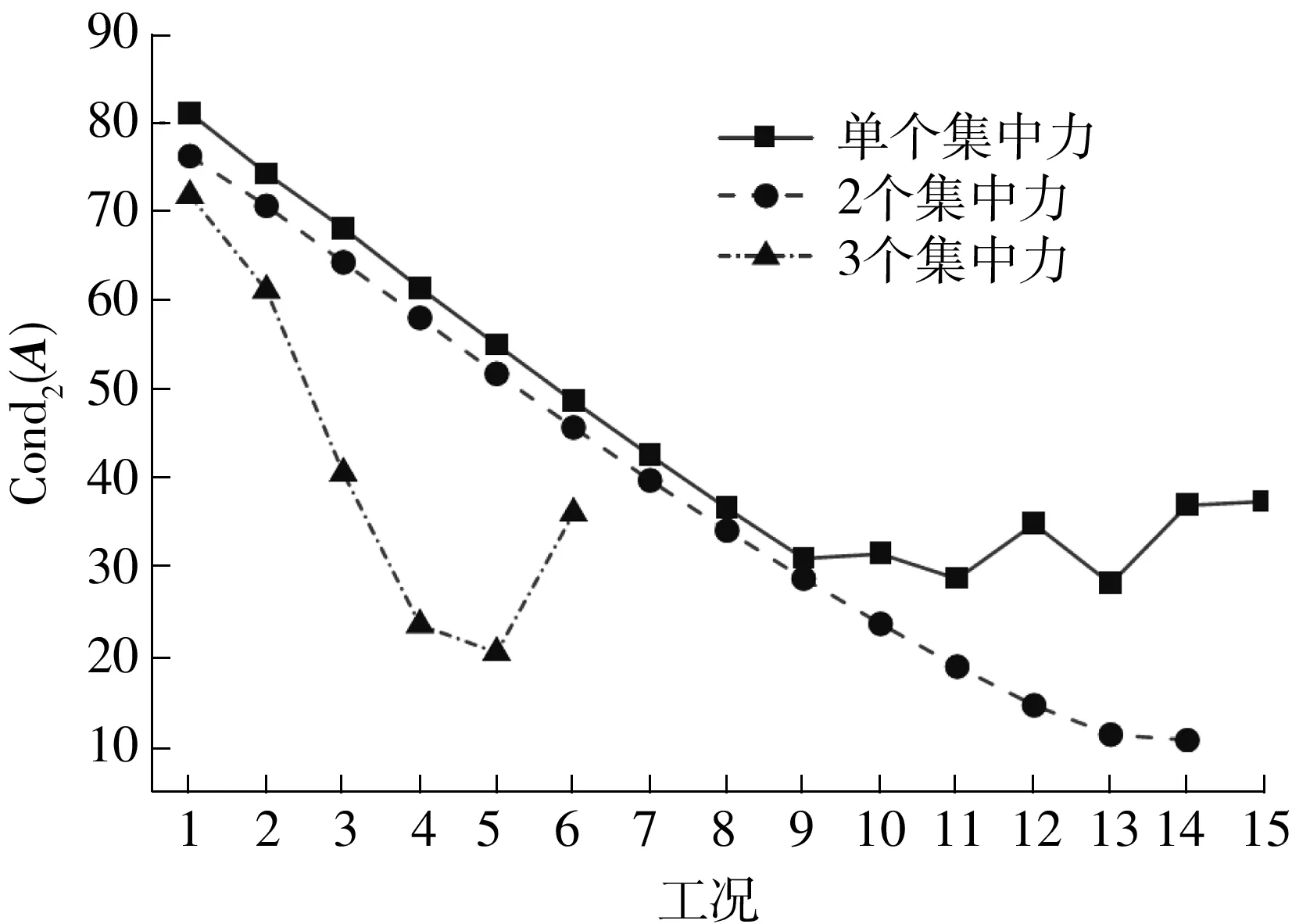
图15 因素5的矩阵条件数Fig.15 Matrix condition number of factor 5

综合图6-图15,从影响Cond2(A)的程度来分析,因素1>因素4≥因素5>因素2≥因素3。在选择合适加载方案条件下,Cond2(A)可取得较小值,识别方程组的稳定性可得到保证。在工程实践中,宜结合实际根据本研究成果合理选择加载方案。

4 测量误差对识别精度的影响

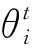
(15)

式中,η为噪声程度,Rand(·)为在[0,1]范围内的均布随机函数。

(16)

表3 当梁分为4段、倾角传感器测量精度为0.01°、噪声程度为3%时各分段ei1)

1)表中抗弯刚度单位为kN·m2;由于倾角传感器测量精度为0.01°,所以有限元模型中提取转角值保留至小数点后3位。

对比表3-表6可知,梁的分段数量越少,能接受测量噪声的程度越高,这与前面关于分段数量对抗弯刚度识别方程组稳定性影响分析的结论一致;倾角传感器测量精度越高,抗弯刚度识别精度也越高;噪声程度是影响抗弯刚度识别精度的主要因素,噪声越大,识别结果相对误差也越大。综合分析,虽考虑了测量噪声影响,但本研究提出的方法仍具有良好鲁棒性,识别结果误差能满足工程精度要求。若能合理控制梁体分段数量,采用高精度传感器,以及通过多次重复测量求平均值等手段减小测量误差,那么采用本研究提出的方法可获得高精度抗弯刚度识别结果。

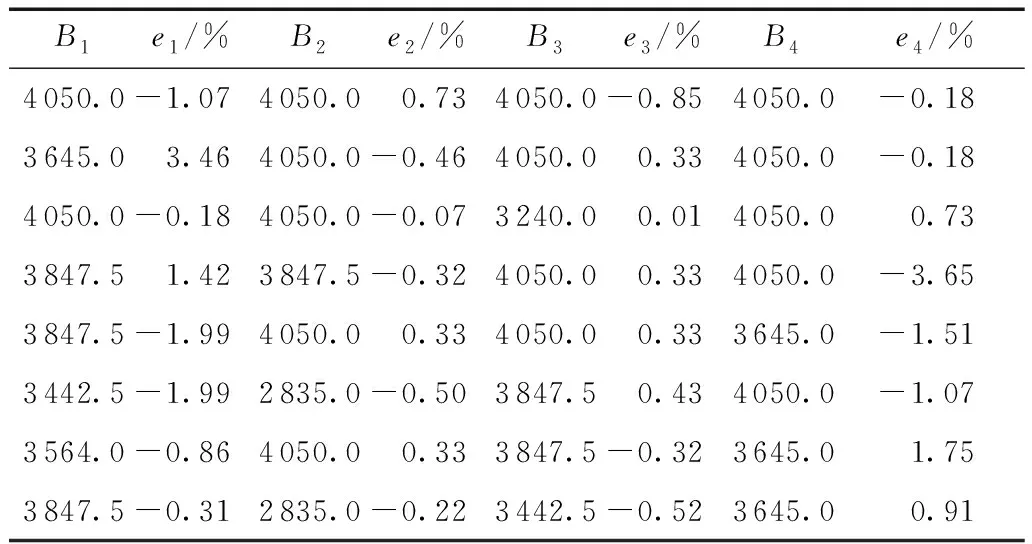
表4 当梁分为4段、倾角传感器测量精度为0.01°、噪声程度为1%时各分段ei1)

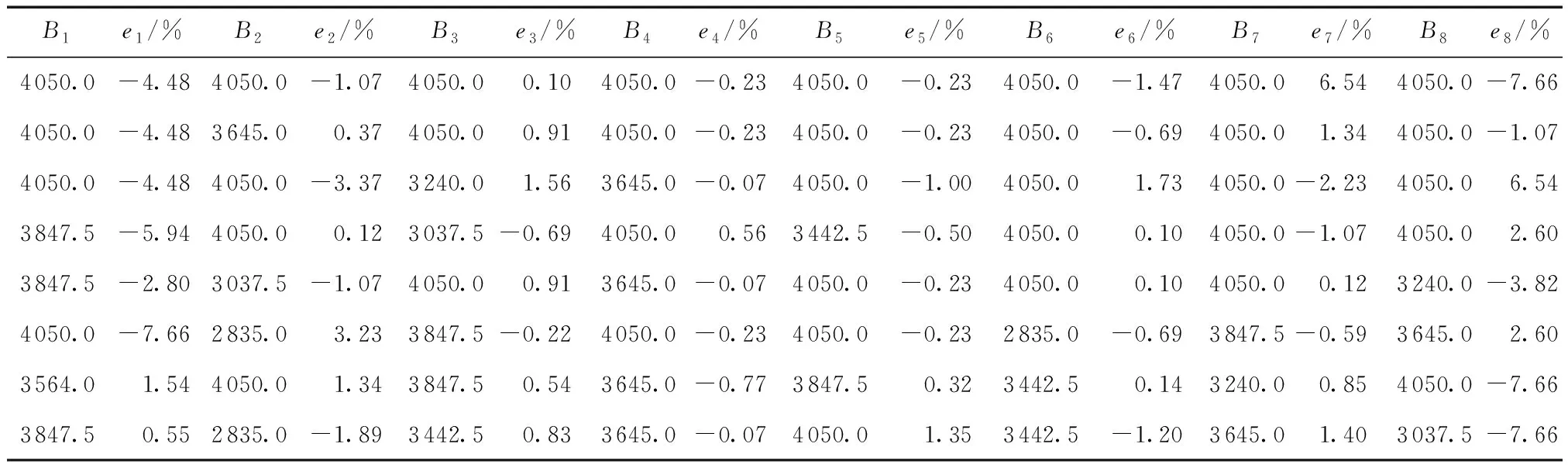
表5 当梁分为8段、倾角传感器测量精度为0.01°、噪声程度为1%时各分段ei1)Table 5 ei of each section when the beam is divided into 8 sections,the accuracy of sensor is 0.01°,and the noise level is 1%

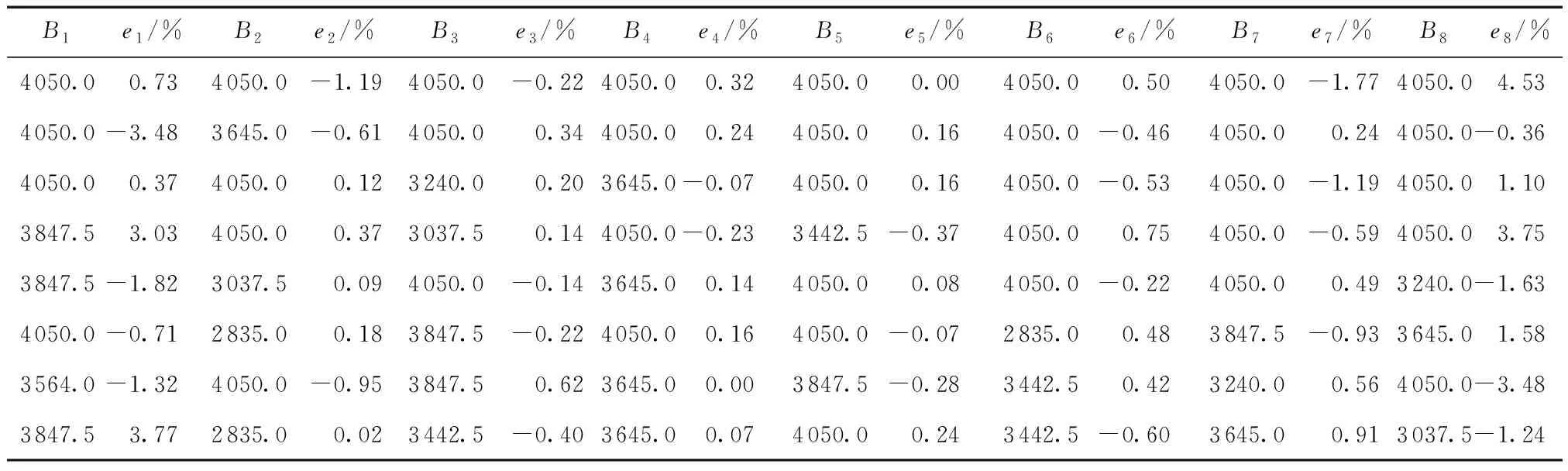
表6 当梁分为8段、倾角传感器测量精度为0.001°、噪声程度为0.5%时各分段ei1)Table 6 ei of each section when the beam is divided into 8 sections,the accuracy of sensor is 0.001°,and the noise level is 0.5%

5 结论

(1)提出了一种基于静力荷载作用下测试转角的简支梁初始抗弯刚度识别方法,有限元数值和试验数据均验证了本方法的可靠性。本方法具有清晰的理论基础,不需复杂的反演算法,不需配合有限元数值模型,不需已知结构截面尺寸、配筋及材料特性等,具有显著优越性。本方法不仅可用于简支梁静载试验结果评估及质量鉴定,而且还可为既有梁结构刚度退化评估及损伤识别提供方法。

(2)本研究的抗弯刚度识别方程组的稳定性与梁体分段数量、作用力大小、类型、个数、作用位置共5个因素有关,其中梁体分段数量、作用力个数和作用位置这3个因素影响程度最大。在选择合适的加载方案条件下,识别方程组的稳定性可得到保证。

(3)转角测量噪声对梁抗弯刚度的识别有显著影响,识别误差随测量噪声的减小而减小。通过合理控制梁体分段数量,采用高精度传感器,以及多次重复测量求平均值等手段减小测量误差,可有效提高梁抗弯刚度识别精度。在加载及测试方法得当的前提下,本研究提出的方法具有良好鲁棒性。