饱和渗透系数变异性对边坡破坏概率的影响

魏红卫 赵凡

(中南大学 土木工程学院，湖南 长沙 410075)

降雨改变了土体原有的渗流场和应力场，边坡孔隙水压力、体积含水率和基质吸力均随降雨入渗呈时空动态变化，且边坡土体在长期的地质作用和风化作用下，土体内部颗粒级配、孔隙比具有一定的随机性，导致土体参数大多表现出变异性，使得边坡失稳具有随机性和不确定性，以边坡安全系数为评价指标的边坡稳定性分析方法并不能完全精准地预测滑坡的发生，其中饱和渗透系数变异性表现最为明显，对边坡稳定性评价的影响最大[1- 3]。运用可靠度分析方法研究边坡失稳破坏逐渐受到众多学者的青睐。薛阳等[4]以三峡白水河滑坡为工程背景，利用半变异函数和核磁共振技术求得了土体饱和渗透系数在竖直方向的波动程度，建立随机场模型分析了饱和渗透系数的竖直波动区间，并对比分析了确定性分析方法和非确定性分析方法下边坡的位移响应，结果表明忽略饱和渗透系数变异性会低估边坡位移。Cho[5]运用平稳随机场模型对饱和渗透系数变异性进行探究，得出了趋势分量会引起饱和渗透系数在沿深度方向上递减，雨水会在边坡内部产生滞水，加速边坡失稳破坏。Zhu等[6]运用蒙特卡罗法对渗透系数进行随机取样，探究了不同降雨强度条件下，渗透系数变异性对边坡地下水位、体积含水率和边坡位移响应的影响。Yang等[7]运用原位试验测得的边坡孔压分布数据，结合贝叶斯公式对二维边坡饱和渗透系数随机场进行推导，构建了二维边坡空间变异的随机场模型。Santoso等[8]以无限长边坡为例，结合随机变量模型探究了饱和渗透系数变异性对雨水渗流的影响，建立了二维边坡稳定性评价体系。覃小华等[9]通过大量试验发现基岩型层状边坡的饱和渗透系数接近于正态分布，并以此探究了在强降雨作用下，基岩型层状边坡的破坏概率等问题。张毛[10]对耀县某黄土边坡进行钻孔取样，对其进行室内渗流试验，并运用统计学方法对饱和渗透系数随边坡高程的演变规律进行探究，推导了饱和渗透系数一维随机变异模型，结果表明，黄土竖直方向饱和渗透系数变异性比水平方向要强。薛亚东等[11]将蒙特卡罗法和局部平均理论结合，生成了饱和渗透系数二维随机场，结果表明，饱和渗透系数垂直相关距离对边坡破坏概率的敏感度比水平相关距离要大。刘力侨[12]推导了饱和渗透系数空间变异性解析解，并结合无限长边坡推导了降雨强度控制阶段和入渗率恒定阶段边坡极限状态函数。

上述研究在建立饱和渗透系数变异性分析框架时均假设边坡入渗边界为常流量边界，这将使得入渗雨水量超过实际情况，使得边坡破坏概率加大。为此，本研究考虑坡面入渗—产流问题对Green-Ampt入渗模型进行改进，得到不同降雨工况下的雨水入渗规律，并以蒙特卡罗法求取随机变量，运用随机变量模型对饱和渗透系数空间变异性进行模型构建，探讨了不同降雨条件下，饱和渗透系数变异性对边坡失稳破坏概率的影响。

1 改进的Green-Ampt入渗模型

Green-Ampt模型较好地反映了有积水情况下的入渗，但该模型并未考虑地表倾斜的情况。基于此，对传统的Green-Ampt模型进行改进，推导供水控制阶段和土体能力控制阶段湿润峰深度与降雨历时的关系表达式，降雨入渗简化模型如图1所示。图中，θw为土体饱和含水率，θi为土体残余含水率，θ为土体体积含水率，p为降雨强度，z1轴表示垂直于边坡坡面方向，x1轴表示平行于边坡坡面方向，γ为边坡倾角。

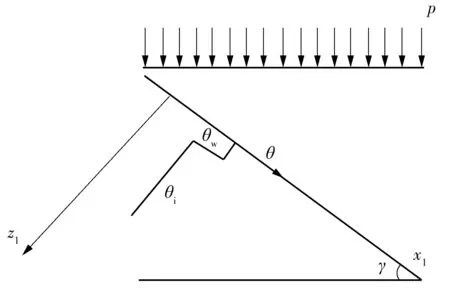
图1 降雨入渗计算模型简图Fig.1 Calculation model of rainfall infiltration

设门槛降雨时间为tp,此时累计入渗量为Ip。

(1)

(2)

(3)

式中，S为基质吸力水头，M为饱和含水率和初始含水率的差值，Ki为达到tp时土体的渗透系数，hi为湿润峰深度,K(h)为不同深度h处土体的渗透系数。Ks为初始时刻的渗透系数，其计算公式为

(4)

同时可得出各个时段的累计入渗量I为

(5)

式中，t为降雨历时，ts为开始积水到入渗量等于Ip所需的时间。

在供水控制阶段，由Darcy定律可知，在坡面z1方向上的入渗率i为

(6)

式中，z表示竖直坐标方向，hw为含水率θw所对应的压力水头。

由坐标变换可得

z=x1sinγ+z1cosγ

(7)

将(7)代入(6)可得

(8)

由式(8)可知，边坡坡面入渗率是由重力梯度和水压梯度两部分所引起的。根据Green-Ampt模型可知，湿润峰以上土体体积含水率几乎为均匀分布[13]，则式(8)的第2项可近似看为零。

在供水控制阶段，坡面z1方向上的入渗率i为

i=pcosγ

(9)

联立式(7)、式(8)可得

(10)

式中，α、n、m为计算参数，与土体类型相关，其中，m=1-1/n。

结合van Genuchten模型：

(11)

式中，H为负压水头。

由式(11)和式(6)可求出湿润峰以上土体的含水率θ为

(12)

根据质量守恒定律、式(10)、式(12)可得降雨历时t所对应的入渗深度zw和孔隙水压力uw:

(13)

uw=γwhw

(14)

式中，γw为土体饱和重度。

再结合Fredlund抗剪强度公式可得边坡安全系数：

(15)

式中：c为土体粘聚力;tanφb为基质吸力增加引起抗剪强度增加的速率,φ为土体内摩擦角。

在土体入渗能力控制阶段，边坡土体处于有压入渗，则可得到降雨历时t所对应的入渗深度zw和边坡安全系数Fs：

(16)

(17)

为进一步验证上述推导的合理性，以均匀型降雨为例，选取降雨强度10 mm/d和40 mm/d的两种工况进行分析，来验证湿润峰深度推导的合理性。将数值模拟结果与运用式(13)、式(16)推导的结果进行对比。

由图2可看出，在降雨0～10 h内，工况1和工况2土体湿润峰深度模拟值和推导值差别很小。在10～72 h内，工况1和工况2土体湿润峰深度模拟值略小于推导值，主要是因为在对Green-Ampt模型进行改进时，并未考虑土体气阻的作用，引起雨水入渗速率和入渗量略微偏大，验证了土体湿润峰深度推导的合理性。

图2 湿润峰深度对比分析Fig.2 Comparative analysis of wetting peak depth

选取降雨强度为25 mm/d，降雨历时为72 h的降雨工况，运用Geo-Studio软件的Seep模块对边坡渗流场进行分析，再运用Slope/W模块的M-P法求解边坡安全系数，将本研究方法的结果与M-P法求解结果进行对比分析，比较结果详见图3。从图3可发现，二者的计算结果较为接近。

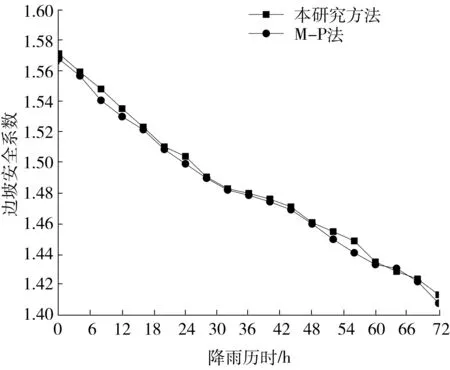
图3 边坡安全系数变化曲线Fig.3 Change curves of slope safety factor

2 边坡失稳破坏概率分析框架

2.1 概率分析方法

在边坡设计或滑坡预报时，常规的确定性分析方法将边坡的土体参数视为确定值，仅能获得一个衡量边坡安全性的指标，即边坡安全系数，而忽略了参数的概率特征。目前常用的考虑土体参数变异性的方法有随机变量模型[14- 15]。

在进行边坡稳定性分析时，将土体参数视为随机变量，运用概率分布函数来对随机变量进行描述，得到边坡研究目标的极限状态函数，将边坡极限状态函数小于零的概率作为边坡达到破坏状态的概率，其表达式为

(18)

式中，f(β)为随机变量联合概率密度函数，g(β)为边坡稳定性的极限状态函数。g(β)=Fs(β)-1，其中Fs(β)为边坡安全系数。

2.2 随机变量Kw的产生

Wang等[16]的研究表明，饱和渗透系数与土体其他参数(如c、γ等)的相关性对雨水累计入渗量的影响较小，为了便于运算，采用随机变量模型进行分析。覃小华等[9]的研究表明，土体饱和渗透系数近似服从正态分布，设其均值为η、标准差为σ、变异系数为CV。此时边坡极限状态函数为降雨历时t、土体饱和渗透系数Kw的函数。同时定义边坡破坏判别函数H(Kw)，其可表示为

(19)

则边坡破坏概率可表示为

(20)

运用蒙特卡罗法对饱和渗透系数Kw进行N次随机变量抽样，则在降雨历时为t时，式(20)可表示为

(21)

3 算例分析

本研究以泾阳南塬某黄土边坡为例，结合杨华[17]和杜玉鹏[18]的研究成果，选取边坡土体物理力学计算参数，见表1。建立简化几何模型，如图4所示。在模型左右边界施加法向约束，模型底部设置为全约束边界，模型上部设置为自由边界。图中，Q2为离石黄土，Q3为马兰黄土。通过在节点处设置流量边界，将边坡入渗边界视为不定边界，当降雨强度大于土体饱和渗透系数时采用水头边界，反之，采用流量边界。

表1 边坡物理力学计算参数Table 1 Physical and mechanical calculation parameters of slope

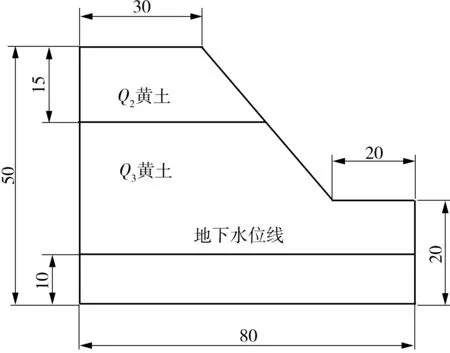
图4 边坡简化模型尺寸(单位:m)Fig.4 Simplified model size of slope(Unit:m)

运用蒙特卡罗法对饱和渗透系数进行随机取样，进而求取不同情况下的边坡失稳破坏概率，运用Matlab对考虑饱和渗透系数变异性的整个过程程序化，具体的流程如图5所示。

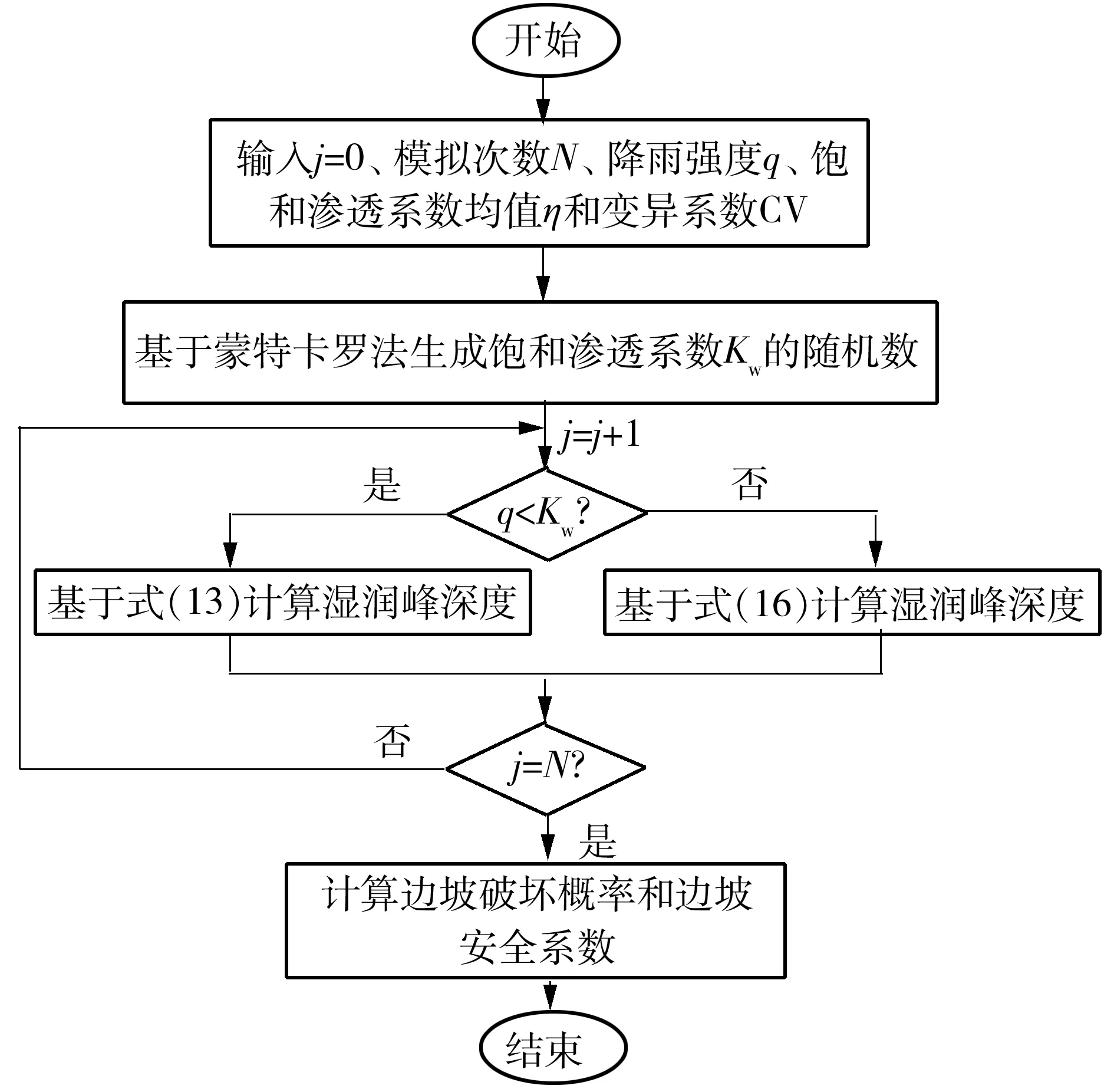
图5 边坡稳定性计算流程图Fig.5 Flow chart of reliability calculation

样本值N越大计算结果越准确，但会降低计算效率，以降雨强度为50 mm/d、降雨历时为48 h为例，得到样本值N与边坡破坏概率的关系，如图6所示，由于N=10 000时，边坡破坏概率处于收敛状态，因此本研究选取的样本值为10 000较为合理。

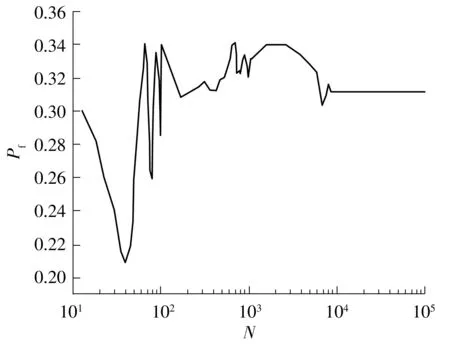
图6 样本值与边坡破坏概率的关系

设定降雨强度为30 mm/d、降雨历时为120 h的工况，分析本研究方法与传统确定性分析方法的差异；运用M-P法得到边坡安全系数为1.10，运用本研究方法得到的边坡安全系数分布直方图如图7所示，在进行10 000次随机模拟得到边坡安全系数小于1的次数为4 412次，说明传统的确定性分析方法不足以说明其危险性。雷坚等[19]基于随机场理论探究了土体参数变异性对边坡稳定性的影响，也得出了类似的结论。

图7 边坡安全系数分布直方图Fig.7 Histogram of slope safety factor distribution

3.1 饱和渗透系数变异性的影响

选取6种不同的饱和渗透系数变异系数，得到不同降雨强度作用下的破坏概率，如图8所示。

由图8可看出，在降雨历时为24 h,降雨强度较小时，土体湿润峰远没有达到临界破坏深度，边坡失稳破坏概率较小，当降雨强度超过40 mm/d时，不同的饱和渗透系数变异系数对边坡失稳破坏概率存在明显差异。当降雨历时为144 h、降雨强度小于25 mm/d时，边坡失稳概率接近于0，但降雨强度由25 mm/d增长到30 mm/d时，边坡失稳破坏概率由0快速增长，表明边坡在经历长时间降雨作用后，当降雨强度增大时，边坡安全系数具有随时间突变的特点，边坡破坏概率也将大幅增加。

在降雨初期，饱和渗透系数变异系数越小，边坡累计失稳破坏概率越小，而在降雨后期，CV值越小其所对应的失稳概率反而越大。为分析产生这种现象的原因，对降雨强度为30 mm/d、降雨历时为144 h的均匀型降雨情况下，CV值为0.25和0.30的边坡进行稳定性分析，图9和图10分别为t=24 h和t=144 h时的边坡安全系数分布直方图。

由图9和图10可知，在降雨24 h时，CV值越大，边坡安全系数分布越广泛，且边坡安全系数大于1的区域相对集中。在降雨144 h时，CV=0.25对应的边坡安全系数集中区域大幅向左移动，使得CV越小的边坡所对应的失稳破坏概率反而越大。

3.2 降雨强度的影响

对变异系数CV=0.15，降雨强度分别为30、40、50 mm/d的情况进行分析，得到边坡破坏概率随降雨历时的分布曲线，如图11所示。

图11 降雨强度对破坏时间的影响Fig.11 Effect of rainfall intensity on failure time

由图11可看出，当降雨强度分别为30、40和50 mm/d时，其对应的滑坡最可能发生时间分别为97.7、64.2和39.4 h，表明边坡滑坡最可能发生时间随着降雨强度增大而缩短，且随着降雨强度增大，滑坡发生的临界区间逐渐变窄，表明在降雨总量相同的情况下，小强度降雨比高强度降雨对边坡的破坏更严重。张硕等[20]开展了黄土填方边坡降雨入渗模型试验，也曾得出了类似的结论。

3.3 降雨历时的影响

以降雨强度为40 mm/d、CV=0.25的边坡为例进行分析，得到边坡安全系数随降雨历时的分布曲线，如图12所示。

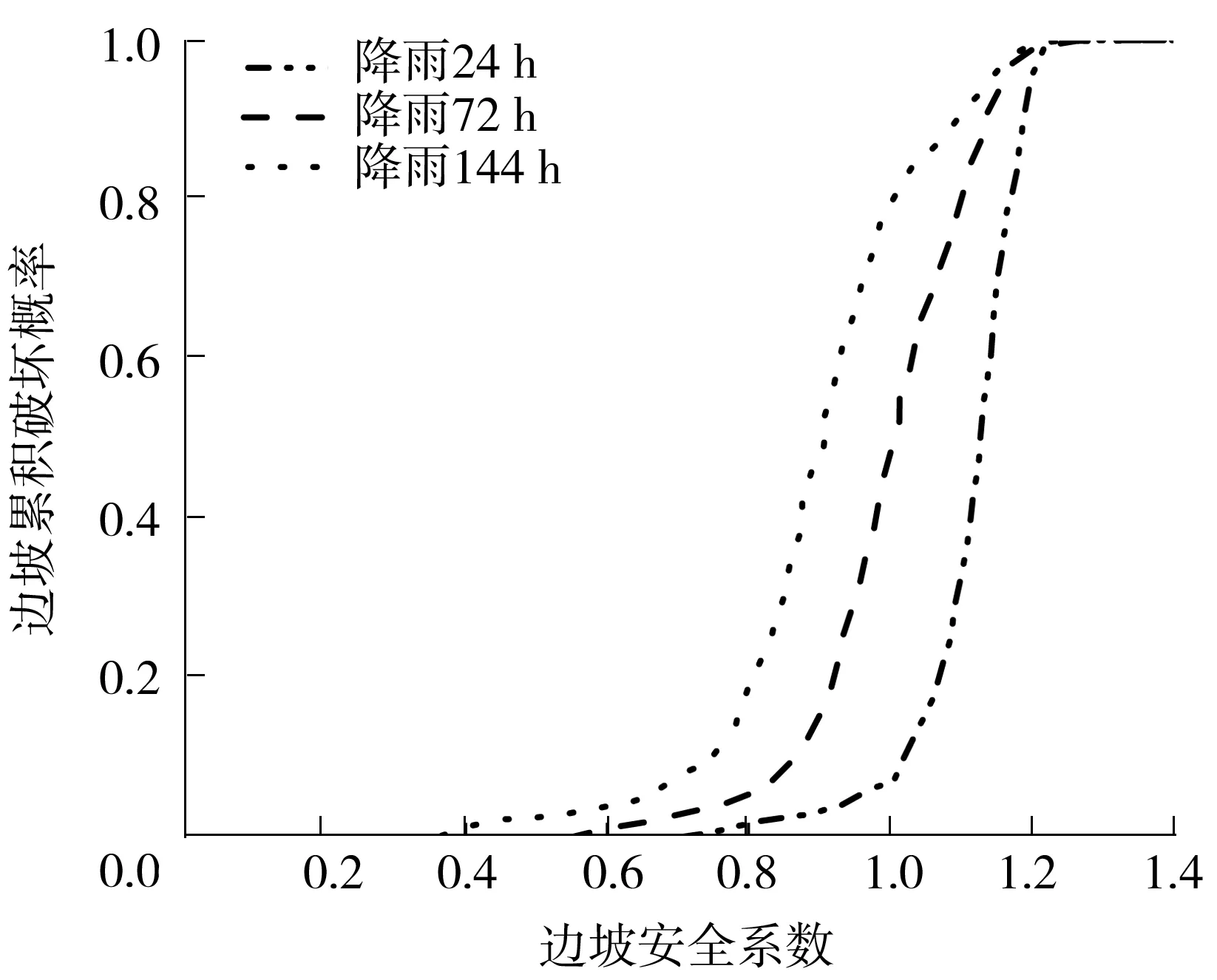
图12 边坡安全系数分布曲线Fig.12 Distribution curves of slope safety factor

由图12可看出，在临界降雨区间内，边坡失稳破坏概率大幅增加，且降雨历时越短边坡安全系数分布曲线越陡峭。同时对比分析不同降雨历时条件下边坡稳定性确定性方法和不确定方法的差异。当降雨历时为24 h时运用Slope/W模块的M-P法对边坡安全系数进行确定性求解，得到边坡安全系数为1.178，而按照本研究的计算方法可得边坡安全系数小于1.178的概率为86%。当降雨历时为144 h时，运用M-P法得到边坡安全系数为0.48，而运用概率分析方法可得边坡安全系数大于0.48的概率为92%。由此可知，对于不同的降雨工况，是否考虑饱和渗透系数会对边坡稳定性评价带来不同程度的影响，当降雨历时较短，忽略饱和渗透系数变异性会过高估计边坡稳定性，而对于降雨历时较长时则与之相反。

4 结论

(1)将边坡稳定可靠度分析方法与传统的确定性分析方法进行对比，结果表明，单凭边坡安全系数的传统确定性分析方法不足以精确地描述边坡稳定性。

(2)在临界降雨历时区间内，边坡失稳破坏概率会骤然大幅增加。当降雨强度较大时，在降雨前期，饱和渗透系数变异系数越大，边坡破坏概率越大，但在降雨后期，由于边坡安全系数集中区域大幅向左移动，造成饱和渗透系数变异系数越小其所对应的边坡破坏概率反而越大。

(3)边坡滑坡最可能发生的时间随着降雨强度增大而缩短。短历时强降雨作用下边坡安全系数具有随时间突变的演化特性，主要诱发浅层滑坡，而长历时小雨作用下边坡安全系数则具有连续性减小的变化特征，主要诱发深层滑坡，且对边坡的破坏也更为严重。

(4)当降雨历时较短时，忽略饱和渗透系数变异性会过高估计边坡稳定性，而对于长历时工况则与之相反。