基于变换空间法的结构参数识别及地震输入反演

杨纪鹏 夏烨† 孙利民,2

(1.同济大学 桥梁工程系，上海 200092;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

基于结构响应观测数据识别结构参数及反演地震动输入具有重要的意义[1]，前者可基于识别结果进行损伤评估，后者可以确定结构在地震作用下的真实输入，也可基于反演结果对区域其他的结构进行动力响应分析，实现震后区域结构快速评估。随着结构健康监测系统应用的发展及普及，国内外学者已开展较多该领域的研究，并取得了一定的成果，如得到广泛应用的扩展卡尔曼滤波和无迹卡尔曼滤波方法[2- 5]。其中加速度响应易于监测，常被作为观测量，其以信息来源来划分，可分为两大类，基于相对观量测和基于绝对观测量。

基于相对加速度的有：Wang等[6]通过最小二乘迭代估计和加权整体迭代-扩展卡尔曼滤波法，识别结构参数的同时反演地震动输入；李杰等[7]通过“统计平均”的思想方法解决复合反演问题，王祥建等[8]在复合反演时引入矩形窗法剔除噪声异常数据；李杰、冯新等[9- 10]建立一种两阶段结构参数识别和地震动输入反演的方法，利用子结构识别部分结构参数，同时反演地震动输入，再根据反演的结果利用加权整体迭代-广义卡尔曼滤波方法识别结构其他参数；王建有等[11]提出了加权平均修正算法，研究了地震动未知情况非比例阻尼模型下结构参数的识别问题；Lu等[12]提出了基于动态响应灵敏度概念，仅从结构输出分两步复合反演系统参数和输入的方法；张坤等[13]提出了一种基于动态响应灵敏度概念，仅利用结构动态响应同步反演结构物理参数和输入。张肖雄等[14]基于扩展卡尔曼滤波法，通过在观测矩阵中引入投影矩阵，实现结构参数识别，利用最小二乘法实现地震动输入反演。郑翥鹏等[15]利用无迹卡尔曼滤波方法，以观测误差最小化为准则，利用最小二乘法求解未知激励，通过将位移响应融入观测向量，消除识别结果漂移。

基于绝对加速度的有：Yang等[16]依据观测到的结构绝对加速度响应及地震输入，基于自适应扩展卡尔曼滤波法，在线识别结构参数(包括非线性参数)，依据参数识别结果判断结构损伤。

Zhao等[17- 18]针对剪切型框架结构在地震动输入未知的情况，通过最小二乘法识别一层以上的结构参数，通过识别结构模态参数得到一层结构参数，最后通过求解一阶微分方程反演结构地震动输入时程，该方法需要对结构所有自由度绝对加速度进行观测。

许煌昊等[19]采用扩展卡尔曼估计和递推最小二乘法对一层以上结构的扩展状态向量和未知作用力进行递推，最后基于数值求解一阶微分方程，识别未观测的地震作用。该方法仅适用于线性结构，对复杂结构以及结构进入非线性后的应用还有待研究。该文献明确指出，只利用绝对加速度无法在识别结构参数的同时完成地震动输入反演，该文献中也利用特征方程协助识别结构参数。雷鹰等[20]将静力凝聚法与扩展卡尔曼滤波法相结合来识别结构参数，同时定量识别结构节点损伤程度，该方法是在地震动输入已知的情况下，只用于结构参数识别。

Shi等[21]提出一种两阶段子空间识别迭代方法。第1步是基于观测到的绝对加速度识别结构模态参数(频率、振型、阻尼比)，基于识别的模态参数估计结构参数；第2步是基于识别得到的结构参数，结合绝对加速度观测量重构地震动输入时程；重复两阶段识别过程直至结构参数识别达到收敛误差要求，同时也得到地震动输入时程。该方法识别精度受预先设定的Hankel矩阵以及观测量维数多少的影响。

实际情况中，地震作用下结构相对地面的相对加速度是不可测的，相对速度或相对位移也是很难测到的，故基于相对量实现结构参数识别及地震动输入反演是很难实现的。以上基于绝对加速度作为观测量的参数识别及地震动反演，只适用于线性系统。对于非线性系统，则需要已知输入。

根据文献[22- 23]，本研究提出基于变换空间法的结构参数识别及地震动输入反演方法。该方法基于绝对加速度观测量，采用线性加速积分法获得结构速度和位移时程，将结构动力方程转换为基于有限元列式的形式，利用最小二乘法识别二层以上结构参数。假定任意相邻3个时刻的地震动输入相等，且等于中间时刻的地震动加速度值，由此提出一种简化的地震动输入反演算法。实际结构自由度数量巨大，不可能做到的全观测量，本方法也可基于有限观测量，识别相应楼层结构参数并反演地震动输入，此时第1、2、3层结构加速度响应必须作为观测量。对于非线性系统，采用等效线性的理念，基于最小方差原则识别结构参数，再在变换空间内实现地震动输入的反演，即本研究所提出的方法可用于非线性系统。首先使用数值算例验证所提算法的有效性，然后通过一个两层钢筋混凝土框架结构振动台试验，验证所提出的算法的实用性和精度。

1 结构参数识别

结构在一维地震动作用下的动力方程为

(1)

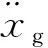
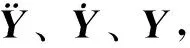
(2)

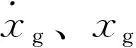
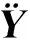
以框架结构为例，设结构的节点数为N，根据文献[7]，式(1)可以改写为

(3)

其中，质量矩阵、刚度矩阵、阻尼矩阵分别为

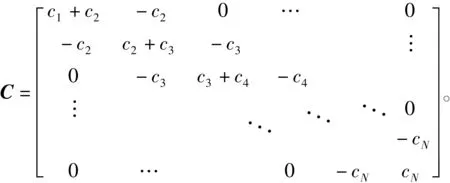
式中，A为系统响应矩阵，θ为结构参数向量。F为结构拟静力荷载向量。由于实际采集到的结构动力响应是离散的，设采样点数为S，则式(3)中各项为：

A=[A(t1)A(t2) …A(tS)]T

(4)

θ=[c1c2…cNk1k2…kN]T

(5)

F=[F(t1)F(t2) …F(tS)]T

(6)

其中：k1,k2,…,kN为层间刚度参数;c1,c2,…,cN为层间阻尼参数。

A(ti)=[A1(ti)A2(ti)]

(7)

(8)

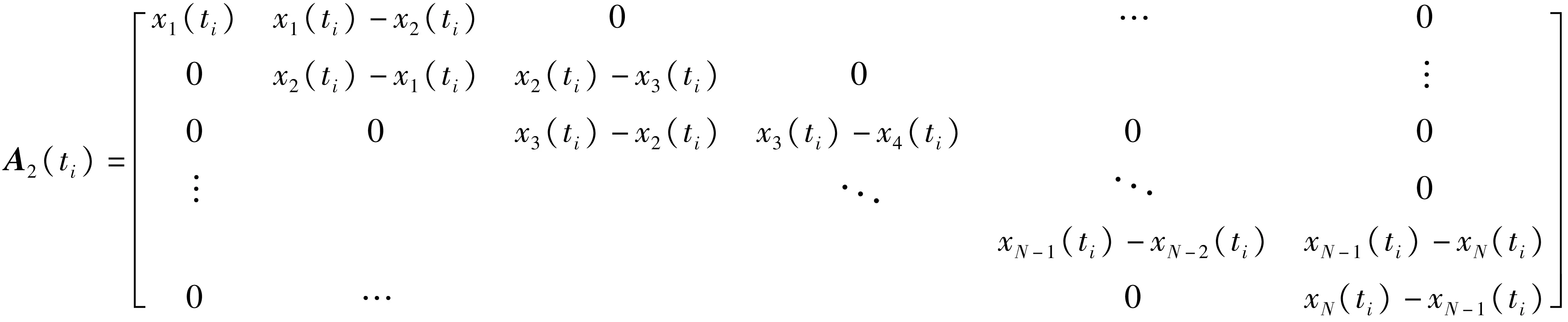
(9)

F(t1)=[f1(ti)f2(ti) …fN(ti)]T

(10)

式(8)、式(9)中i=1,2,…,S，且在任一时刻ti，

(11)

xp(ti)-xq(ti)=yp(ti)-yq(ti)

(12)

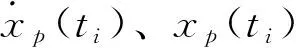
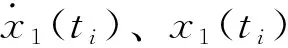
θ=[ATA]-1ATF

(13)

但是，通过加速度积分得到速度和位移时，存在初值未知的问题，而且通过加速度积分得到位移和速度存在趋势项，目前虽然在这方面已有一些研究成果，实际中由于噪声干扰，通过积分得到速度和位移，再相减得到的层间相对速度和位移得到的识别结果误差很大。为此，将动力方程转换到变换空间内，再用式(13)求解2层以上结构参数；变换空间内的某个样本与原物理空间的3个连续采样时刻相对应，变换空间内的运动方程为[22- 23]：

(14)

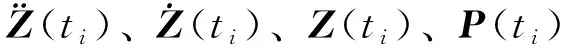
(15)

(16)

(17)

P(ti)=2F(ti)-F(ti+1)-F(ti-1)

(18)

通过式(13)可求解1层以上的结构参数。接下来求解第1层的刚度参数，第1层层间刚度可以通过刚度消去法[24]，或通过特征方程求解[18]，第2种方法可在有限测点下实现，本研究使用第2种方法。结构特征方程为

(K-ω2M)φ=0

(19)

对于第i阶振型，式(19)可写为

(20)

将刚度矩阵及质量矩阵代入，取方程组的第1行方程，第1层层间刚度可表示为

(21)

式中,φi为结构第i阶振型向量，ωi第i阶自振圆频率，φ1i、φ2i分别是第i阶振型向量第1个和第2个元素。

2 地震动输入反演

将式(2)代入式(1)得

(22)

式(22)可以改写为

(23)

根据框架结构阻尼矩阵C和刚度矩阵K的形式特点，式(23)等式右边只有第1层(底层)不为零，即

(24)

其中，结构参数m1已知，k1、k2、c2在结构参数识别章节已经识别得到，c1仍未知。采用线性加速度假定，在变换空间内式(24)可以改写为

(25)

可得地震动输入反演递推公式为

(26)

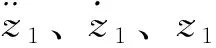
假定地震开始的前两个采样时刻地面加速度为0，根据式(26)依次求得后续地震动加速度时程。式(26)是一个递推过程，数值仿真表明(数值仿真时c1取理论值)，误差会随时间步的增加而不断累加，最终导致计算结果发散。为了避免误差的累积，消除地震动输入反演的递推形式，假定任意相邻3个时刻地震动加速度相等，且等于中间时刻的加速度，即

(27)

则式(26)可简化为

(k1+k2)z1(ti)-k2z2(ti)](-k1Δt2)-1

(28)

此时，c1仍为未知的，式(24)中等式左边阻尼项的比重相对于刚度项小得多，可以忽略，则式(28)中与结构阻尼相关的项可去掉，式(28)可进一步简化为

k2z2(ti)](-k1Δt2)-1

(29)

式(29)即为最终得到的简化地震动输入反演表达式，只需基于部分观测量识别得到k1、k2即可实现地震动输入反演。

3 数值仿真

选取一个12自由度的剪切型框架结构来验证所提算法的有效性，将该结构简化为一集中质量模型。假定地震作用下结构仍处于线性状态，其运动方程如式(1)所示，其中质量矩阵、刚度矩阵、阻尼矩阵中各元素如下所示：

m1=m2=m3=m4=8×105kg,m5=m6=…=m12=4×105kg,k1=k2=k3=k4=1.3×109kN/m,k5=k6=k7=k8=1.2×109kN/m,k9=k10=k11=k12=1.0×109kN/m,c1=c2=c3=c4=4×106kN·s/m,c5=c6=…=c12=2×106kN·s/m。

结构前3阶频率为1.076、2.720、4.626 Hz，前3阶阻尼比为0.87%、1.98%、3.21%。观测1-3层绝对加速度，为模拟实际监测中噪声的干扰，在监测信号中加入均方根(RMS)为5%的高斯白噪声。通过随机子空间法(SSI)识别得到模态参数,如图1所示。由识别得到的稳定图可以看出，该地震作用下结构的振动能量主要集中在低频，参数识别时使用低通滤波器对观测信号进行滤波降噪，滤波截断频率为15 Hz。

图1 模态参数识别结果Fig.1 Identified results of modal parameter

首先通过式(13)识别第2层、第3层阻尼参数、刚度参数；然后选取第1阶模态信息识别结果计算结构第1层刚度k1，结构参数识别结果见表1。

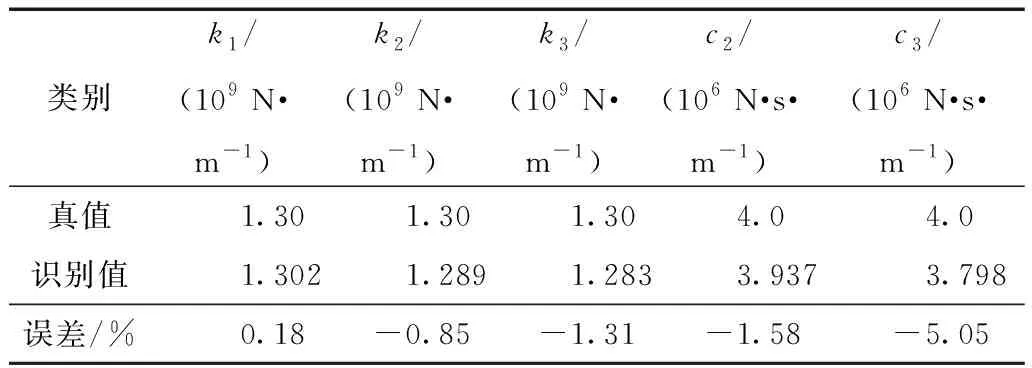
表1 结构参数识别结果Table 1 Identified results of structural parameter

由表1可以看出，本研究所提的参数识别算法具有较高的精度。即使在观测量中加入5%噪声，刚度参数识别的最大误差也只为-1.31%，阻尼参数的最大误差也只为-5.05%。因为刚度参数与阻尼参数数量级相差较大，阻尼参数的识别结果劣于刚度参数，这也是参数识别目前普遍存在的问题。

识别得到结构参数后，通过式(29)反演地震动输入，反演结果如图2所示。由图2(a)可以看出，反演得到的输入与实际输入在整个时程上吻合较好，即持续时间吻合良好；地震动加速度的峰值(PGA)在第2 s左右出现(见图2(b))，实际值为-3.126 3 m/s2，反演结果为-2.930 2 m/s2，误差为6.27%，说明在峰值处有一定误差，但也满足工程需求；图2(c)示出了功率谱密度曲线，两者吻合较好，说明反演结果真实代表了实际输入的能量分布。

图2 地震动输入反演结果Fig.2 Inversion results of seismic input

4 试验验证

4.1 试验描述

为进一步验证所提出的基于变换空间和最小二乘法对结构参数识别和地震动输入反演算法的有效性和实用性，开展两层钢筋混凝土框架结构振动台试验[25- 26]进行验证。框架结构层高0.98 m，长2.18 m，宽1.5 m。各层堆放铁块，底层质量为2 990 kg，顶层质量为2 870 kg，试验模型如图3所示。加载采用EL Centro地震波，试验时测得台面加速度和各楼层绝对加速度，采样频率为200 Hz。

图3 两层钢筋混凝土框架试验模型

试验分3个工况，台面峰值加速度分别为200、400和1 200 gal，分别对应结构无损、轻微损伤和严重损伤，试验工况如表2所示。

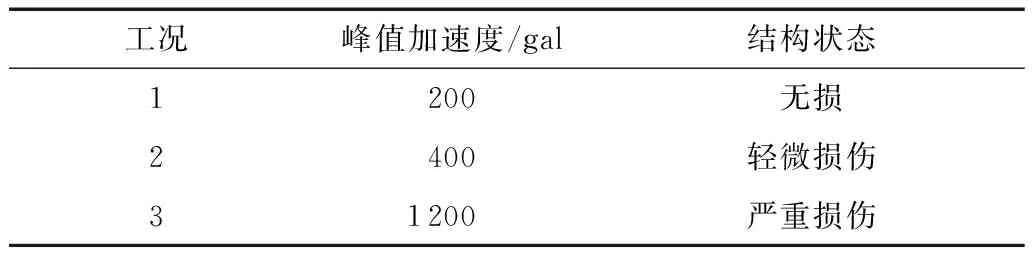
表2 试验工况[25- 26]Table 2 Test conditions [25- 26]

4.2 参数识别

将两层框架结构简化为具有两个平动自由度的集中质量模型(见图4)，x1、x2分别代表第1层、第2层相对于地面的位移,k1、k2代表层间刚度，c1、c2代表层间阻尼。

图4 两自由度线性系统示意图Fig.4 Sketch map of 2-DOF linear structural system

通过式(13)、(14)识别一层以上结构的参数，利用SSI方法识别结构基频和振型，再利用式(21)识别一层刚度系数。基于识别得到的频率，在参数识别及地震动输入反演时，采用低通滤波对绝对加速度信号进行降噪，工况1、2的滤波截断频率为50 Hz，工况3的滤波截断频率为15 Hz，结构参数识别结果见表3。

表3 两层混凝土框架结构参数识别结果

表4 不同工况初值选取表Table 4 Initial values for different cases

工况1的结构刚度、阻尼参数识别时程如图5所示。由图5可以看出，当地震激励荷载较小时，结构处于线性状态，由于待识别的刚度、阻尼参数初始值很接近真实值，故收敛曲线基本为一条直线。不同工况下，本研究及UKF-KI识别的结构参数见表5。

图5 结构参数识别结果(工况1,UKF)

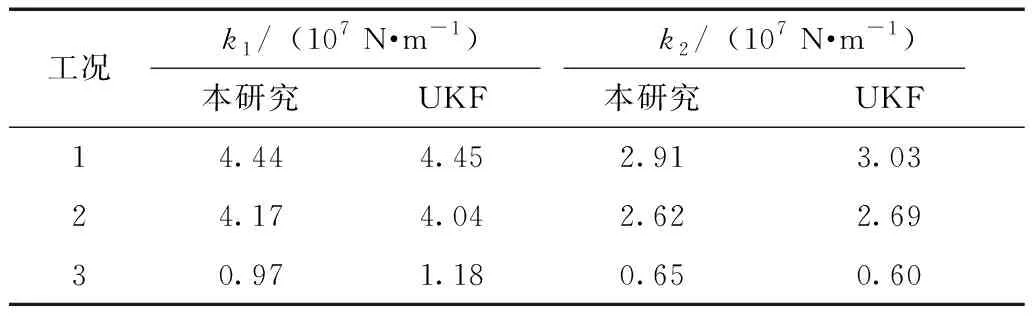
表5 刚度参数识别结果对比Table 5 Comparison of identified stiffness parameters

由表5可知，在工况1、工况2的情况下，结构处于线性状态，两种方法识别出的刚度值非常接近，最大误差为3.96%。工况3中，地震动峰值加速度达到1 200 gal，结构损伤严重，进入强非线性状态，此时基于等效线性化理念采用线性识别方法识别非线性系统，发现本研究提出的方法与UKF识别结果出现较大误差，最大误差达到-17.8%。根据识别得到的结构参数，反算不同工况下结构基频，结果见表6。

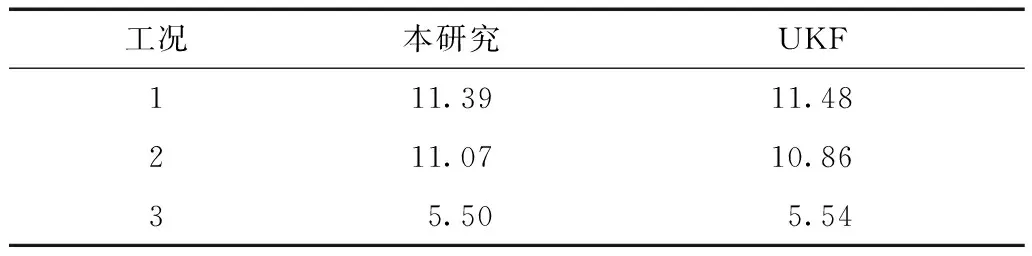
表6 频率识别结果对比

由表6可以看出，3种工况下，通过UKF识别的参数反算得到的结构基频与本方法得到的结构基频非常相近，最大误差为1.93%，这表明：①线性系统(工况1、工况2)UKF参数识别结果是准确的，用本研究提出的方法识别参数是精确的；②结构进入强非线性时，通过SSI方法识别结构频率，再通过等效线性化方法进行参数识别及地震动输入反演的理念是可行的。

为进一步验证识别参数的准确性，根据识别的结构参数正分析结构响应，此时，结构第1层层间阻尼系数c1是未知的，此处仅作为对识别参数准确性的验证，取

(30)

以工况1(线性系统)进行验证，可得c1=2.85×104N·s/m，实测及正分析重建各层绝对加速度响应的结果如图6所示。

从图6可以看出，根据识别得到的参数重建的结构响应和实测响应吻合得很好，进一步验证了本研究提出的方法参数识别的精确性。

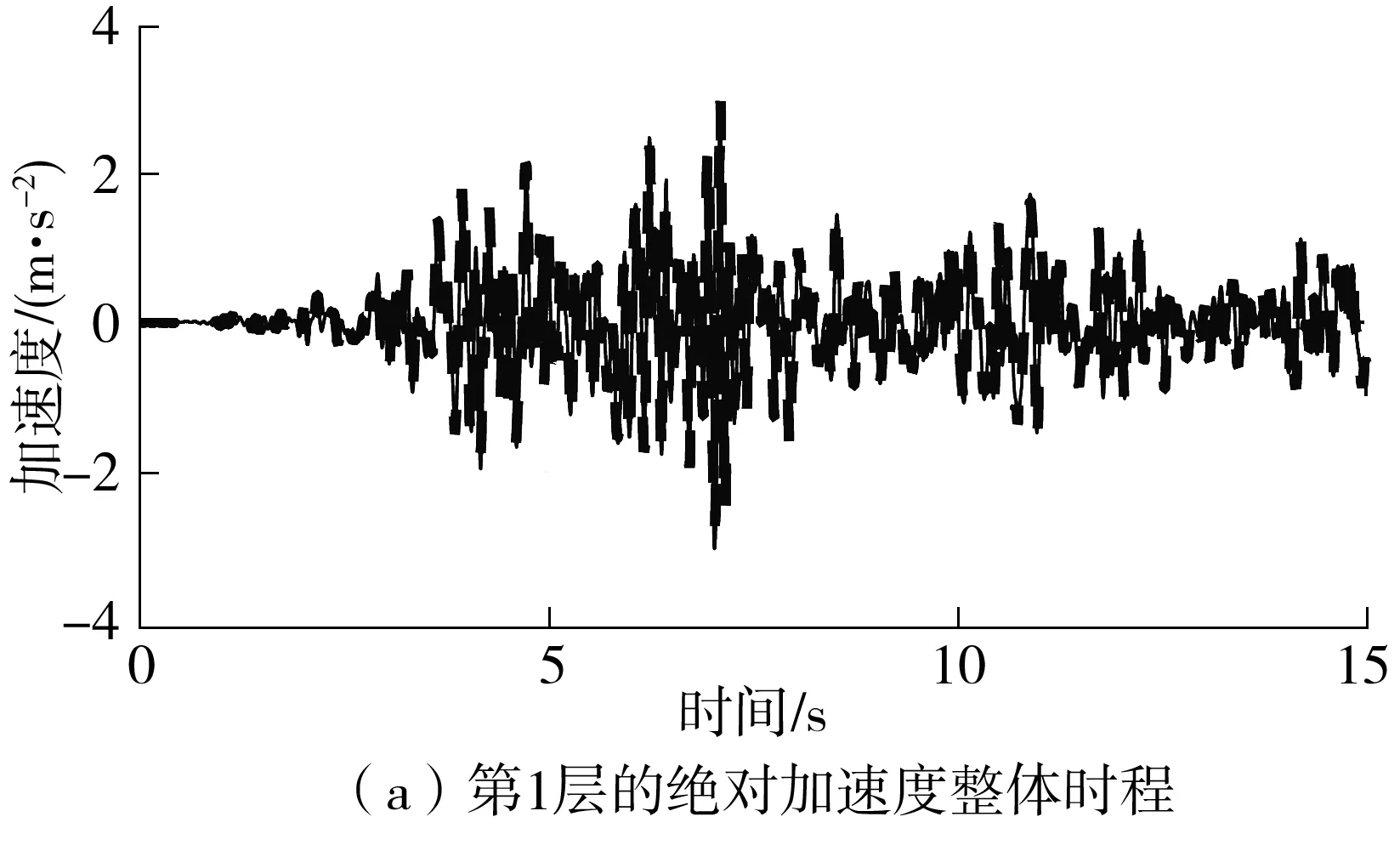
图6 绝对加速度响应对比图(工况1)Fig.6 Comparison of absolute acceleration responses(case 1)

4.3 地震动输入反演

根据识别得到的结构参数，由式(29)反演地震动输入。尽管反演算法是基于线性系统推导的，但参数识别是基于最小方差原则求解的，对于非线性系统，识别得到的参数代表结构在全时段的“平均值”，即全时段等效线性刚度与阻尼；而假定系统在一个规定的微小时间段内为线性，则所提出的反演算法在这一微小时段内也是适用的，采用这一思想对全时段数据进行处理，则反演算法也可适用于非线性系统。篇幅所限，现只将工况1、工况3的反演结果分别展示。

4.3.1 工况1

工况1中，实测台面峰值加速度为200 gal，SSI识别得到的结构基频为11.4 Hz，结构处于线性状态，反演得到的时程曲线及功率谱如图7所示。

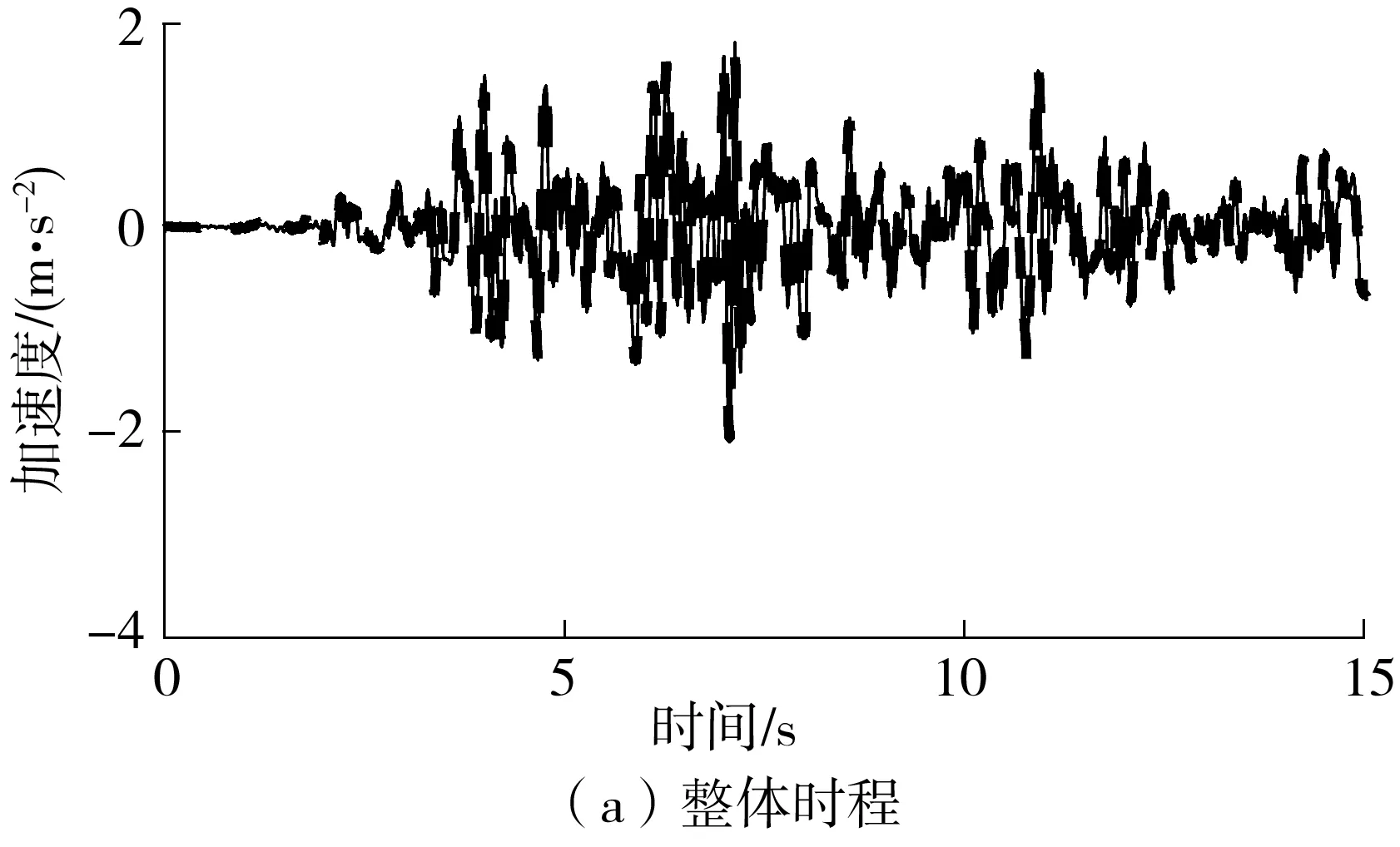
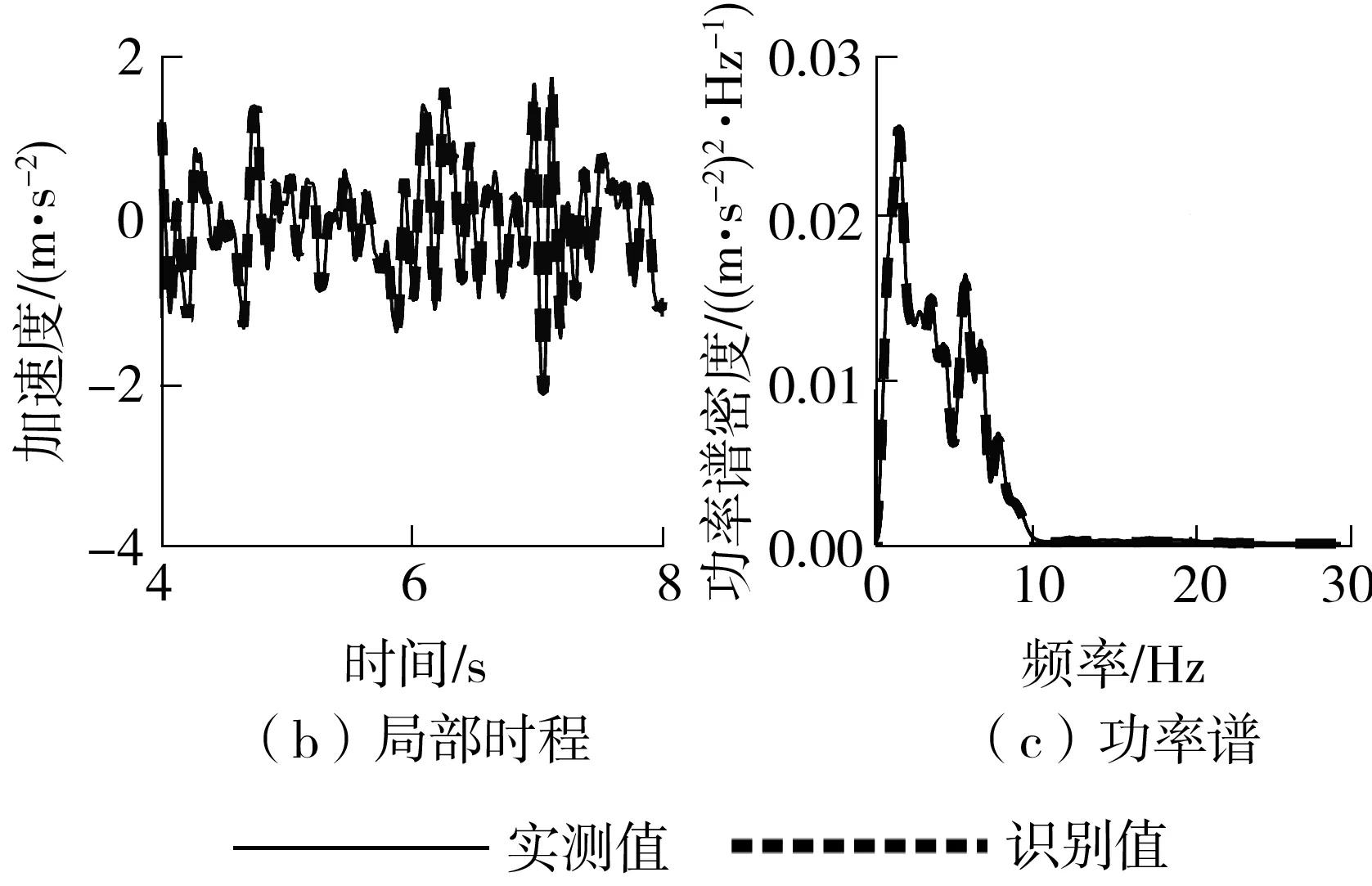
图7 地震动输入反演结果(工况1)Fig.7 Inversion results of seismic input(case 1)

由图7可以看出，本研究提出的地震动反演算法在地震动持续时间、峰值和功率谱上，很好地重现实际地震动输入；其中，实测台面PGA为-2.129 0 m/s2，反演值为-2.100 2 m/s2，误差为1.35%，说明所提算法在线性系统下具有很好的精度。

4.3.2 工况3

工况3中，实测台面峰值加速度为1 200 gal，SSI识别得到的结构基频为5.50 Hz，约为无损结构基频的一半，表明结构出现严重损伤，结构进入非线性阶段。仍用基于线性系统的参数识别及地震动反演方法对数据进行处理，反演得到的时程曲线及功率谱如图8所示。

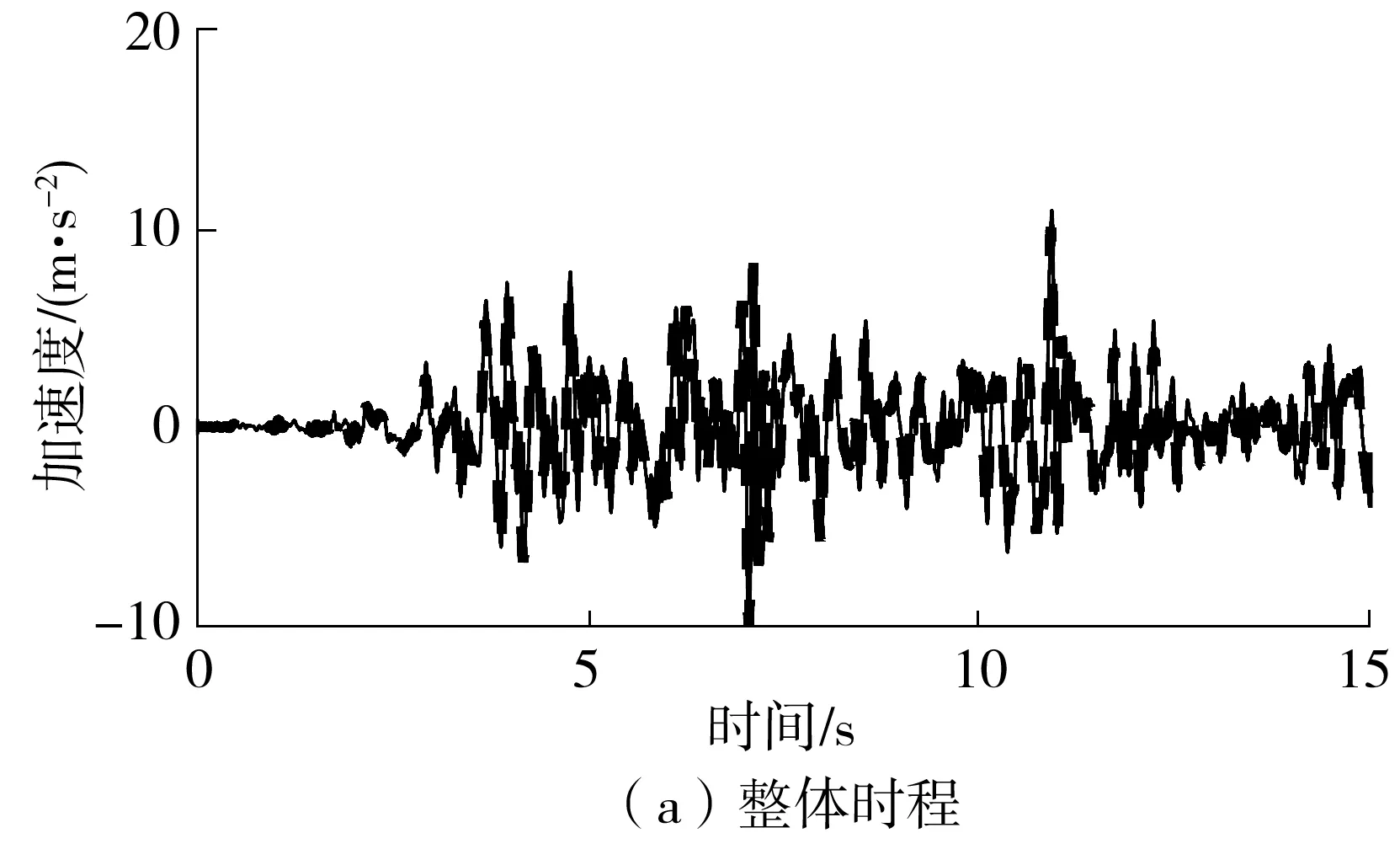
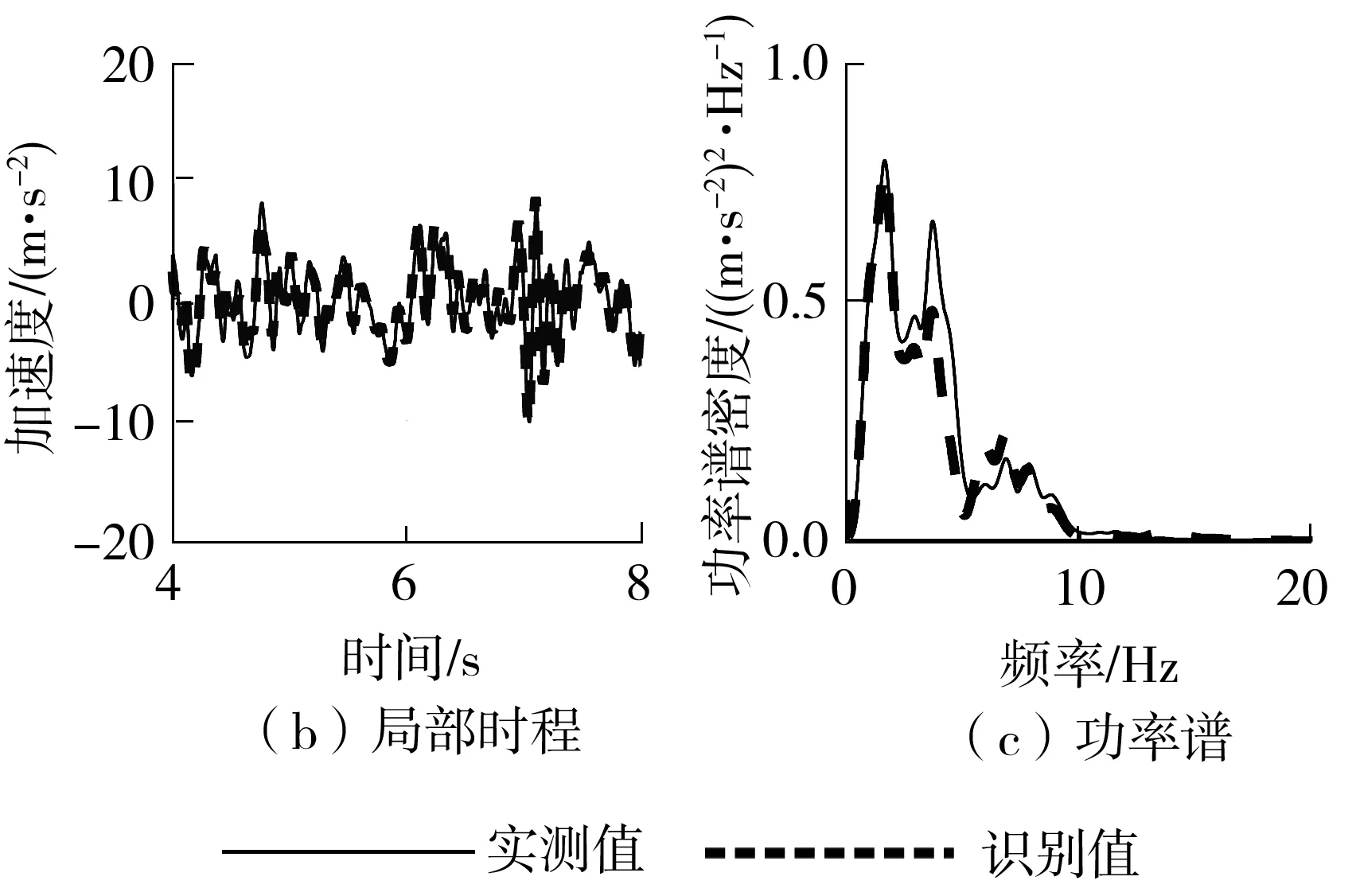
图8 地震动输入反演结果(工况3)Fig.8 Inversion results of seismic input(case 3)

由图8可以看出，结构出现严重损伤后，所提出的结构参数识别及地震动输入反演方法仍然具有较好的识别精度及实用性。在整体时程上，反演结果与实测台面加速度吻合得相对较好；实测台面PGA为10.993 6 m/s2，反演值为10.129 9 m/s2，误差为7.86%，说明所提算法在非线性系统下仍具有相对较好的精度；在功率谱方面，结构出现严重损伤后刚度下降，频率降低，故基于监测数据反演得到的地震动在低频区间(0～5 Hz)与实测值吻合良好，高于该频率后，仍体现了该地震动能量的总体分布状况。

综合工况3的地震动反演结果可知，即便结构出现严重损伤，结构进入强非线性阶段，反演得到的地震动时程数据仍能很好地反映真实地震动输入的低频特性。

以上两个工况试验结果表明，本研究提出的基于变换空间的最小二乘参数识别方法参数识别精度高，重建响应与实测响应基本吻合。对于非线性系统，识别的结构参数是基于最小方差原则得到的，识别得到的是等效线性化的参数，所提出的地震动输入反演算法虽然是基于线性系统推导的，但对非线性系统也有一定的适用性。

5 结论

本研究分析了未知输入情况下框架结构参数识别及地震动输入反演问题，提出了在变换空间内利用最小二乘法识别结构参数的方法，通过假定任意相邻3个采样时刻地震动加速度相等，且等于中间时刻的地震动加速度值，提出一种简化的地震动输入反演算法；通过数值模拟及两层钢筋混凝土大尺度模型振动台逐级加载试验对所提方法进行了验证，得到如下结论：

(1)所提出的算法计算稳定，不存在不收敛问题(即无需给定初值，递推过程不依赖前一步结果，不会出现发散现象)，且参数识别精度高，从理论上避免了因加速度积分导致速度、位移初始值未知及存在趋势项的问题，且可基于部分观测量实现输入反演。

(2)当系统为非线性时，基于等效线性化理念，所识别的结构参数可准确表征结构整体动力行为，其结果可为下一阶段的地震动输入反演所使用，即基于线性系统推导的地震动输入反演方法，同样适用于非线性系统。

(3)反演结果能够准确再现未知输入低频区间的功率谱特性，可基于此功率谱分析其他建筑，即所提出的方法可用于区域结构及建筑群的抗震性能演绎分析。