基于实时交通流的事故风险评估与分析模型

马新露 樊博 陈诗敖 马筱栎 雷小诗

(1．重庆交通大学 交通运输学院，重庆 400074；2.西南交通大学 交通运输与物流学院，四川 成都 610031)

我国高速公路正依托各类高新技术朝着信息化、智慧化的方向发展，然而相应的交通安全管理却主要沿用一些传统方法，这显然无法适应现阶段以及未来高速公路交通安全管理的需求和可持续发展。据国家统计局发布的资料显示[1]，2019年年末全国民用汽车保有量为26 150万辆、全年道路交通事故万车死亡人数为1.8人；同时数据显示，2019年我国高速公路总里程已达14.95万公里。高速公路为国民经济和社会发展提供了强有力的支撑，预防交通事故对建设智慧高速公路、保障高速公路安全运行和提升运营效率至关重要。

由于事故兼具随机性和偶然性，难以对其作出高度准确的预判，因此研究人员常用“是否存在事故风险”来描述这种不确定性。区别于传统事故频率预测，现有事故风险评估研究根据预测技术的不同主要可分为两大类：一类是将当下时刻的事故空间特征借助图卷积等技术作为输入，再引入交通和道路环境特征，使用深度学习等方法建模学习交通事故模式并实现事故风险预测[2]；另一类以实时交通流数据为主要输入，通过训练和区分事故与非事故状态下的不同交通流特性来捕捉事故前兆特征，使用分类算法建模区分事故与非事故，从而实现事故预测[3- 5]。这两类方法中，前者研究对象多为路网，后者多为路段。在第2类研究中，Xu等[6]提取美国高速公路某路段交通流数据，建立了贝叶斯Logistic回归模型，识别出了不同道路服务水平下的事故风险交通流参数。孙剑等[7]实现了上海市快速路的道路主动风险评估，并对比多种算法模型精度后发现贝叶斯网络模型预测能力最佳。Kwak等[8]将韩国高速公路某干线划分为基本路段和匝道附近两种路段类型，以遗传编程技术建模，结果表明，考虑拥堵状态和路段类型能有效提升事故风险预测效果。除上述文献外，建立事故风险评估模型的方法还有遗传算法[9]、二元概率模型[10]以及病例对照Logistic回归[3]等。

由于事故样本远少于非事故样本，若要把所有交通流数据都作为样本进行建模则较为复杂，而解决类似非平衡数据分类问题时，可通过欠采样的方式来处理数据[3]；且既有研究证明[3,9,11]，通过抽样的方式从非事故交通流数据中抽取部分样本来代表非事故交通流状态下的交通流特征是可行的，因此这类研究在建模的样本设计阶段多数是基于欠采样思想，即以病例-对照研究方法构建实验样本[3,6- 8,11- 14]。例如，Hossain等[15]以日本某两条检测器分布均匀的路段为研究对象，利用病例-对照研究方法建立实验样本集，使用随机多项式Logistic回归模型确定事故影响因素，基于期望最大化聚类算法识别出事故风险下的交通流状态。Xu等[6]、Kwak等[8]在开展事故风险评估相关研究时，也均是采用病例-对照研究方法建立实验样本集。

在事故风险评估模型中，研究人员将每起事故视作“病例”，然后按一定比例(配对比)抽取非事故数据作为“对照”来提取交通流数据，从而构建实验样本[3,6- 8,11- 14]。然而在任何交通系统中，事故往往是小概率事件，其时空特征都具有一定的零膨胀性。尤其是在短期分钟级角度下，与事故相关的交通流数据明显少于非事故状态下的交通流数据，若从全样本数据中抽取极小部分的非事故数据作为对照样本建模，然后在该抽样样本集中评估模型，则容易导致剩余大量未用于建模的交通流特征无法被模型学习，最终导致模型整体预测能力不理想。

为研究交通流特征与事故之间的关系，本研究建立基于支持向量机的事故风险评估模型；同时，以不同配对比构建多个实验模型进行实验，采用受试者工作特征曲线(ROC)下面积AUC值作为模型评价指标，探索不同病例-对照配对比对模型预测能力的影响。

1 数据准备

1.1 数据来源

以图1加州I-880 N高速公路某40.4 km路段为研究对象，检测站编号为402880至400608。

提取该路段2018年间交通事故数据和实时交通流数据。其中，提取事故记录1 389 起，由于本研究探讨的是交通流特征与事故间的关系，因此剔除掉因车辆故障、货物洒落或信息不完整等事故记录后，最终用于本研究的事故记录共873 起；交通流数据包括所监测断面的流量、速度和占有率等，由平均铺设密度为0.43 km的检测器组采集而得，检测器采集频率为30 s/次。表1示出了研究路段中检测器组的分布情况。

图1 本研究实验路段Fig.1 Experimental segments in this research

表1 检测器组分布情况Table 1 Distribution of spacing between detector stations

1.2 实验样本设计

1.2.1 变量分析与构建

研究[3- 4,6- 8,11- 14]证明，流量、速度和占有率，以及这3 个参数在集计时间内(通常为5 min)所有检测数据返回值的标准差、变异系数是影响事故风险的重要因素。其中，流量、速度和占有率通常为集计时间内的均值或总和，标准差和变异系数表示集计时间内参数的相对变异和离散程度；此外，考虑到检测器组铺设密度的不规则性可能会对观测交通流参数变化造成一定的影响，本研究再引入这3个交通流参数的“变异率”作为新变量，用以描述检测器组之间不同距离下交通参数的变化情况，其取值为每个集计时段内每相邻两组检测器间的交通流参数差与其距离的比，其描述了在集计时段内单位距离下的交通流参数的变异和离散程度。

文献指出，用以描述事故风险的交通流参数来自事故发生位置上、下游各2 组检测器断面内，因此将提取事故发生位置上、下游最近2 组检测器的交通流数据，按上游到下游的顺序依次对检测器组命名为Up2、Up1、Dn1和Dn2。然后提取每起事故发生前20 min[16]上、下游各2组检测器的交通流数据，并以5 min[3- 4,7,11- 14]为单位将其集计到4个时间间隔内。此时构建变量MNα,β，其中，M代表平均值(A)、标准差(S)、变异系数(C)或变异率(R)；N代表流量(V)、速度(S)或占有率(O)；α代表检测器组Up2、Up1、Dn1或Dn2；β代表时间间隔，取值为t1至t4，其中t1离事故发生时刻最近。例如，变量RODn2,t3代表在某起事故发生位置下游第2个断面、在事故发生前第3个时间间隔内参数占有率的变异率。

综上，本研究构建了共计4 个交通流运行状态观测指标×3个交通流参数×4个检测断面×4个时间片段，即192个交通流变量，所有变量的时空分布情况见图2。

图2 交通流变量时空分布Fig.2 Spatio-temporal distribution for traffic flow variables

1.2.2 实验样本集构建

为在样本设计阶段有效消除其他混杂因素(时间、地点和道路环境等)对建模和研究结果带来的影响[3,6- 8,11- 14,17]，本研究将采用病例-对照研究构建实验样本集。病例-对照研究是一种用于探索病因的流行病学方法，即以某人群内患有某疾病的所有个体作为病例组、未患该疾病但存在可比性的其他个体作为对照组，对比两组对象是否曾暴露于危险因子及其暴露程度，从而推断危险因子与该疾病有无关联及其关联程度。Abdel-aty等[3]最早将该方法应用于事故风险评估模型，以配对式抽样方法提取交通流数据，其原理是提取某起事故发生前的交通流数据作为事故样本(病例组)，对应于该起事故在相同时间、空间等条件下未发生事故时的交通流数据作为非事故样本(对照组)；通过提取多起交通事故相应的病例、对照样本即完成实验样本集构建；然后再利用条件Logistic回归建立事故风险模型，实现事故风险评估。

既有研究证实，使用病例-对照研究方法能有效地以欠采样的方式用非事故交通流的部分样本表述非事故交通流特征，因此后续大多相关研究在设计实验样本时均采用该方法。既有研究分别使用了不同配对比(例如1∶4[9,13- 14]、1∶5[3- 4]、1∶8[8]、1∶10[7]、1∶30[15]以及全样本[16]等)构建实验样本集；而在流行病学中常用1∶1和1∶2作为配对比，并有资料显示增大病例数量、增大病例-对照配对比能在一定程度上增强模型表达能力[17- 18]；研究表明，当病例-对照配对比增大到1∶4“左右”时，统计性能并不会显著增强[19]。因此现有事故风险评估研究中，大多借助“经验法则”即以1∶4作为事故-非事故配对比构建实验样本集。

本研究采用配对式抽样方法匹配对照样本。匹配原则为：针对每起事故，提取与其相同地点、相同周天、相同天气情况(天气数据来自美国国家气象数据中心，并根据能见度与降雨强度将天气情况划分为晴天、雨天、雾天、雾霾与其他)以及相同时间节点所对应的非事故交通流数据，同时为消除事故背景下产生的噪声数据，还需事先剔除事故路段在事故发生后1 h的交通流数据[16]。

为研究不同配对比对模型的影响，探索模型在何种事故-非事故配对比的实验样本集上能充分学习到事故前兆特征，本研究将基于不同配对比构建多个实验样本，包括1∶4-1∶10和1∶15、1∶20，以及随机配对比。其中“随机配对”是指针对每起事故随机地配对4-6、4-8、4-10、4-12、4-16、4-18和4-20 条非事故交通流数据。同时，在提取变量和构建样本时，需要对样本中每条数据增设字段“病例标签”，其取值为1或-1，各自代表病例组或对照组样本，最终得到各实验样本集后，再按7∶3的比例随机将各样本集划分为训练集与验证集。

2 模型建立

2.1 基于随机森林的变量选择

为防止众多交通流变量之间的交互作用对观测单个变量与事故风险之间的关系造成影响；同时为避免输入变量过多给模型带来过拟合风险，从而影响后续模型预测精度，有必要筛选出部分影响事故风险的重要因素后再进行建模。

以往研究中，变量筛选方法有条件Logistic回归分析法[8]、后退法[13]和逐步回归法[16]等。本研究将采用随机森林(RF)算法来筛选变量。RF通过集成多个决策树提升模型泛化能力和降低过拟合风险，无需单独交叉验证测试数据集即可获得无偏误差估计；且其本身能够自然地避免多个变量间的交互作用[20]，可利用RF自身提供的平均基尼系数下降值(MDG)对构建的变量进行排序，变量MDG越大则说明该变量越重要，即借助MDG排序筛选出影响事故风险的重要变量。

使用RF需确定决策树数量和各节点变量数，通过观测最小和最恒定的袋外错误率(OOB)来确定决策树数量；每个节点处变量数设为变量总数的平方根[21](本研究取值为14)。基于1∶4 构建的实验样本，本研究使用CART算法构造的120 个决策树，实现了获得最小和最恒定的OOB，图3示出了MDG排前30的变量的取值情况。

表2示出了前8 个变量(图3 分界线及以上)的MDG值具体取值情况。

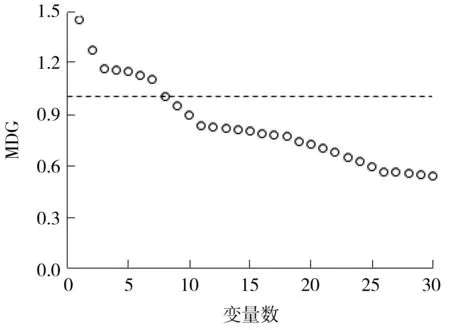
图3 MDG值前30的变量Fig.3 Top 30 variables ranked by MDG

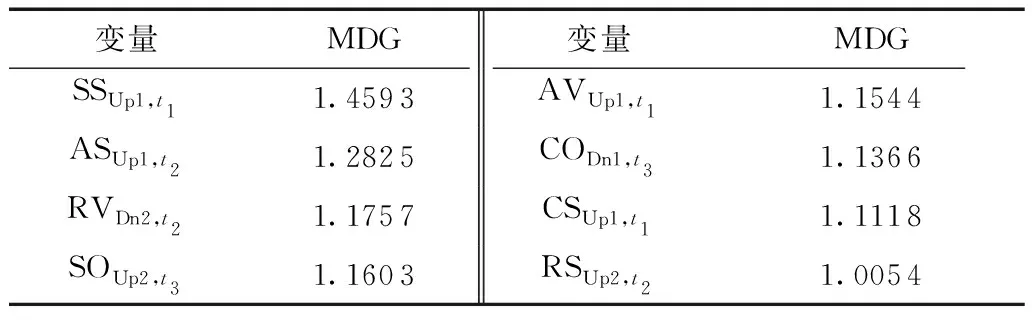
表2 变量重要性排序Table 2 Variable importance ranking

表2中的结果显示，排序中前两个变量均与速度相关，因此可知，速度参数的动态变化对事故风险的影响更为显著。空间上，事故位置上、下游均可观测到事故前交通流的紊乱现象，相比而言，上游交通流参数的变化对事故影响较大一些；时间上，事故发生前0～5 min(t1)和5～10 min(t2)对预测事故风险最为敏感。由于表2中8个变量基本涵盖了相关交通流参数的时空变化特征，考虑到过多的变量会给模型带来不必要的计算压力[16]，本研究选择这8个变量来构建事故风险模型。

2.2 支持向量机模型

支持向量机(SVM)可通过已有信息求得最优解，因此能很好地应对小样本或样本有限的情况；并且其基于结构风险最小化准则，具有较好的推广能力；同时其可通过多种核函数将样本映射到高维特征空间，将问题转换为线性约束条件下的凸二次规划问题求得全局最优解，以此解决非线性问题。考虑到本研究构建的实验样本数据规模较小、维度较高等因素，选择SVM建立事故风险评估模型。

线性SVM通过构建超平面wTxi+b=0来区分由带有病例标签Y=(y1,y2,…)的训练样本集X=(x1,x2,…)所构成的样本集合D={(x1,y1),(x2,y2),…,(xn,yn)}。其中：xi表示样本；w和b为超平面的法向量和截距；yi∈{1,-1}，即1为事故，-1为非事故。然而，样本维度较高极有可能会导致其线性不可分，此时非线性SVM借由核函数φ将实验样本映射到高维空间后，再构建超曲面对事故与非事故样本进行训练分类：

(1)

式中：wTφ(xi)+b=0为超曲面；θi为拉格朗日乘子；κ(xi,xj)为核函数，与SVM性能优劣高度相关。因此本研究将采用多种常用核函数建模，根据实验结果来确定模型最佳核函数，引入的核函数包括线性核、多项式核、高斯核以及Sigmoid核，表达式分别为：

(2)

(3)

κ(xi,xj)=exp(-γ‖xi-xj‖2)

(4)

(5)

式中：d为多项式核函数最高项次数，考虑到模型对计算能力的要求，本研究取d为3；a、c和γ为超参数，其中γ大于0。

2.3 模型评价指标

在数据不平衡的分类任务中，用准确率作为模型评价指标时，无法反映出少数样本被识别出的重要性，难以准确反映分类效果。在这种分类任务中，不仅需要模型输出较高的准确率，还同时需要模型输出较低的虚警率，即要求模型在正确区分事故交通流的同时，还要保证对事故和非事故的误判率足够低。由于ROC曲线同时考虑了模型分类性能的真阳性率和真阴性率，研究人员通常用ROC曲线下的面积AUC值作为模型的评价指标。

本研究将以真阳性率、真阴性率、ROC曲线及AUC值作为模型评价指标。计算上述评价指标，首先引入混淆矩阵，具体见表3。

表3 混淆矩阵Table 3 Confusion matrix

根据表3可计算：

(6)

(7)

(8)

式中，TPR为真阳性率，FPR为假阳性率，TNR为真阴性率。可利用TPR和FPR绘制ROC曲线计算AUC指标。

3 实验结果及讨论

3.1 变量选择结果与分析

本研究由随机森林筛选出影响事故风险最显著的变量包括SSUp1,t1、ASUp1,t2、RVDn2,t2、SOUp2,t3和AVUp1,t1等。其中，SSUp1,t1、ASUp1,t2和AVUp1,t1与文献[3,12- 13]所选择的重要变量一致；同时，本研究新引入与变异率有关的变量RVDn2,t2和RSUp2,t2也在重要变量集合之中。

根据表2示出的重要变量筛选结果可知，在事故发生前一段时间内，事故位置上游和下游的交通流均出现了一定程度上的交通紊乱现象。对比已有研究，其中SSUp1,t1与文献[4]和[22]建模所使用的变量相同，其表示事故位置上游车辆行驶速度的离散程度；ASUp1,t2也是多数研究[3,9,12- 13,20]建模所使用的变量之一，其指出事故位置上游速度与非事故情况相比较低[3,13,20]；RVDn2,t2为事故发生前5～10 min下游(Dn2)车流量的变异系数，文献[13]针对这一变量指出，事故发生前下游车流量的差异性是引发事故的重要因素，具体表现为该差异性越大，事故风险则越大；而文献[4]则显示下游流量波动性越小，事故风险越大；文献[13]和[4]均以标准差来衡量流量的波动性。本研究的变量RVDn2,t2在描述流量的波动性的同时还考虑了检测器组间的不同间隔对交通参数变化的影响。

3.2 事故风险评估

3.2.1 支持向量机事故风险模型

基于1∶4 病例-对照配对比构建实验样本，使用Python语言建立SVM模型，并配合不同核函数进行实验;模型中超参数在多次组合实验后保证能使准确率维持在较高水平下调参取值。图4示出了不同核函数下模型输出的ROC曲线。

图4 不同核函数下SVM模型的ROC曲线Fig.4 ROC curves of SVM model in different kernel functions

然后，根据4 种核函数下SVM模型各自的ROC曲线计算各自曲线下的面积，即AUC指标。表4示出了不同核函数下模型的AUC结果，表5示出了本研究Sigmoid函数下SVM模型结果与部分既有研究的预测准确率对比。

表4 不同核函数下SVM模型的AUC指标Table 4 AUC of SVM model in different kernel functions

表5 本研究与既有研究的模型结果对比

从事故风险评估预测精度或模型AUC指标来看，本研究建立的SVM事故风险模型与部分既有研究相比具有一定的优势；且4种核函数下的SVM模型均能在一定程度上预测事故风险。因此，在本研究中使用由RF筛选出的重要变量构建的SVM模型能有效预测事故风险；同时结合表4可知，高斯核和Sigmiod核下SVM模型的AUC指标相对较高，是建立SVM事故风险模型的最佳核函数。

3.2.2 病例-对照配对比对模型的影响

为探索模型中病例-对照配对比与模型预测能力之间的关系，针对不同配对比建立的实验样本集，以高斯核和Sigmoid核分别构建SVM事故风险模型进行实验，得到模型的AUC指标，见表6。

表6 不同配对比样本下SVM模型的AUC指标Table 6 AUC of SVM model in different matching ratio samples

由表6可见，不管是以高斯核还是以Sigmoid核建立的SVM模型，AUC指标总体上均随配对比的增大而升高。这是由于随着实验样本中非事故样本数量增加，交通流信息也随之丰富，模型对事故交通流与非事故交通流之间的差异“学习”得更加充分，其解释和表达能力增强则预测能力上升，最终模型AUC指标增长。然而也可同时看出，两种核函数下的SVM模型的AUC指标并不是随着配对比的增大始终呈现显著升高趋势的，因此表7示出了相较于以1∶4构建的实验样本，其他不同配对比下SVM模型AUC的平均增长率情况。

表7中的结果进一步表明，模型AUC指标总体上随配对比增大而升高，尤其是当配对比从1∶4逐渐提高到1∶10时，AUC平均升高了9.095%，增长明显。可见提高配对比能在一定程度上增强模型预测能力；但当该比例提高到1∶15、1∶20时，AUC平均增长率为9.409%、9.722%，与1∶10构建的样本实验结果相比仅上升了0.314、0.627个百分点，此时继续提高病例-对照配对比，对模型的预测能力并无显著提升，即与交通流因素相关的信息对事故的解释能力已经无法再提升。在流行病学中，病例-对照研究方法在病例-对照配对为1∶4的基础上，继续增大该比例对统计指标的显著性无明显增强效果；然而本研究实验结果说明，将病例-对照研究方法应用于事故风险评估模型中构建实验样本时，事故-非事故配对比无须沿用流行病学中由“经验法则”所建议的1∶4[11,17- 19]配对比，可根据道路安全管理的实际需求、所设目标AUC值等对该值进行取舍。

表7 不同配对比样本下SVM模型的AUC增长率

同时表7也显示，当使用随机配对比来构建样本进行实验时，模型AUC指标同样较为稳定，并且以随机比例配对构建实验样本进行实验时，不仅能提高相对的模型表达能力，还能降低一定的计算负荷。

4 结语

基于高速公路事故数据和实时交通流数据，由RF确定建模变量后构建了SVM事故风险预测模型，其能根据交通流运行实况有效地评估预测事故风险。同时实验结果表明，高斯核和Sigmiod核是构建SVM事故风险预测模型的最佳核函数。研究发现，模型AUC指标随病例-对照配对比的增大而升高，但当该比例增大到一定程度时，AUC增长放缓，对模型的预测能力无显著提升作用。因此可根据实际情况对该比例进行衡量取值。实验结果可为后续实现在线预测事故风险提供理论支撑。

本研究仅以SVM构建事故风险模型探索样本配对比对模型的影响，后续还将采用其他算法建模实验。同时，还可通过划分交通流不同运行状态、划分事故形态类型等，研究不同交通运行环境下的事故风险交通流的差异，以此提升模型预测能力。