Q690D高强钢的疲劳性能试验研究

康澜 洪书涛

(华南理工大学 土木与交通学院，广东 广州 510640)

随着现代土木工程向“更高、更长、更柔韧”的方向发展，高性能材料(例如高强度结构钢材)有了用武之地[1]。相比普通钢，高强钢结构在受力性能、建筑使用功能、施工工艺以及社会经济和环保效益等方面具有显著优势。随着钢材屈服强度的提高，屈强比增大而断后伸长率减小，屈服平台长度缩短甚至消失，高强钢的应变强化效应并不明显，疲劳和断裂性能尚不明确[1]。疲劳破坏是钢结构中重要的破坏形式之一[1]。与其他破坏形式不同，疲劳破坏没有前兆，构件突然发生断裂，对钢结构的安全性能产生重大危害[1]。然而，针对高强钢，目前我国的钢结构规范[2]并没有相应的疲劳曲线可以参考。因此，非常有必要针对Q690D高强钢开展疲劳性能研究，分析疲劳应力与循环次数之间的关系，得到适用于Q690D高强钢材的疲劳曲线，为高强钢结构疲劳寿命预测提供科学依据。

国内外学者对不同强度等级的钢材已开展了相关的疲劳性能试验研究[3- 12]。Sakai等[3]通过试验观察了金属在正常寿命状态和高周疲劳状态下的应力-寿命(S-N)曲线，观察到正常寿命状态下晶界裂纹、表面夹杂物和加工裂纹等不同的断裂模式，发现在高周疲劳状态下的裂纹主要是由于局部力学行为损伤引起。Lu等[4]的研究解释了金属内夹杂物尺寸对疲劳寿命离散性的影响，表明夹杂物诱发断裂的S-N曲线与夹杂物的尺寸有关，并给出夹杂物尺寸影响下夹杂物诱发断裂的S-N曲线。Hu等[5]的研究表明：裂纹萌生是由于金属表面存在缺陷，并在疲劳荷载下持续扩展引起。武会宾等[6]在对Q500qE桥梁钢的高周疲劳性能研究中发现，钢材中的细小夹杂物和针状铁素体的片条结构能够有效地减缓裂纹的萌生和扩展。Liu等[7]综述了高强钢在超高周疲劳下的S-N曲线预测方法，并在此基础上提出了基于Basquin方程的预测方法，验证了该方法预测结果与实际结果的一致性。刘汉青等[8]通过对Q345钢材进行高周疲劳性能试验，提出了基于热力学框架的预测材料固有耗散能的模型，试验表明通过循环荷载下疲劳试件在初始阶段的温度变化率可以很好地预测Q345钢的高周疲劳极限。施刚等[9]对Q390GJD钢材开展了疲劳性能试验研究，给出了能够描述其疲劳性能的S-N曲线，并对试件断面特征进行微观分析，发现疲劳断面能观察到明显的疲劳辉纹，瞬间断裂面能观察到典型的韧窝特征。程峰等[10]对Q420B和Q420C两种钢材进行了疲劳性能试验研究，得出两种钢材的S-N曲线并与规范进行对比，发现试验结果的疲劳强度远高于规范计算值。施刚等[11]对Q460D高强钢开展了疲劳性能试验研究，该试验批次的钢材疲劳离散性较大，试验得出该种钢材的S-N曲线并与规范进行对比，发现试验得到的S-N曲线比规范计算值大。郭宏超等[12]对Q460D钢材和钢材焊缝连接疲劳性能进行了疲劳试验研究，拟合了母材及焊缝的S-N疲劳曲线，揭示了疲劳裂纹的扩展规律。

目前，针对钢材疲劳性能的研究主要集中在普通钢[1]，而针对高强钢特别是Q690D高强钢疲劳性能的试验研究并不多，还没有系统的试验结果[1]。然而，目前很多大跨度、超高层结构都趋向于采用高强钢，高强钢疲劳性能研究就显得尤为重要。因此，本研究通过对Q690D高强钢开展高周疲劳性能试验，依据试验结果提出Q690D钢材的S-N曲线，并与其他强度等级钢材的疲劳曲线进行比较，相关结果可为高强钢结构的疲劳寿命预测提供科学依据和数据支持。

1 试验概况

1.1 单调拉伸试验

本研究所有试件均采用国内钢厂生产的10mm厚Q690D钢板，采用全板厚取样方式。为得到Q690D钢板的力学性能参数，首先根据《金属材料 拉伸试验 第一部分：室温试验方法》(GBT228.1—2010)[13]开展Q690D钢板的静力拉伸试验。Q690D静力拉伸试件尺寸如图1所示，Q690D钢材化学成分见表1。所有试验结果由3根拉伸试件的平均值计算得到。本研究中Q690D钢材的力学性质如下：屈服应力为800 MPa，弹性模量为217 GPa，泊松比为0.29，抗拉强度为840 MPa，延展率为0.09。由拉伸试验获得的工程应力-工程应变曲线如图2所示。

图1 静力拉伸试件尺寸(单位：mm)Fig.1 Static tensile specimen size(Unit：mm)

1.2 高周疲劳试验

疲劳试验是本研究的重点。根据《钢及钢产品力学性能试验取样位置及试样制备》(GB/T 2975—1998)[14]中对于取样方式与钢板厚度关系的规定，试验材料的取样方式为全厚度取样。由于疲劳试验结果往往离散性比较强，每个应力等级准备了多个试件，以便获得更加准确的数据。根据《金属材料 疲劳试验 轴向力控制方法》(GB/T 3075—2008)[15]分别在9种不同的应力水平下开展高周疲劳试验；从最高的应力水平开始，以逐步降低应力水平的顺序进行试验，通过记录不同应力水平下试件破坏时的循环加载次数，得到Q690D的S-N曲线。

根据《金属材料 疲劳试验 轴向力控制方法》(GB/T 3075—2008)[15]中的相关规定，疲劳试验的试件表面状态对试验结果有一定的影响。因此，为消除试件表面锈蚀对最后疲劳试验结果的影响，在疲劳试验之前，试件表面必须打磨光滑。疲劳试验的试件尺寸如图3所示。疲劳试验试件如图4所示。

图3 疲劳试验试件尺寸(单位:mm)Fig.3 Fatigue test specimen size(Unit:mm)

1.2.1 试验装置

本试验采用的试验装置为如图5所示的MTS疲劳试验机，试件固定位置如图6所示，阴影部分为试件的夹持区域，夹持端之间的距离为150 mm。试件夹持时对试件进行同轴度检查，从而保证试验过程中轴向力的稳定传递。

图5 MTS试验机Fig.5 MTS test machine

图6 疲劳试件固定位置(单位:mm)Fig.6 Fixed position of fatigue specimen(Unit:mm)

1.2.2 试验条件

(1)应力比

本次试验的应力比v是指施加循环疲劳荷载过程中试件截面的最小应力与最大应力之比，如式(1)所示：

v=Smin/Smax

(1)

式中，Smin为试件截面最小应力，Smax为试件截面最大应力。为避免试件发生受压屈曲，取应力比v为0.1。最大和最小应力均为拉应力。

(2)交变荷载和频率

本次试验中的交变荷载波形如图7所示，图中纵坐标σ为截面应力，横坐标t为时间。荷载的频率取决于试验机的类型和试件本身的刚度。本试验所使用的试验装置为MTS试验机，其频率范围为15～20 Hz。当采用最大频率20 Hz、最大应力为605 MPa以上的高应力时，MTS试验机的性能无法满足试验要求。由于试验装置性能的限制，本次试验中试件最大应力在605 MPa以下时，试验装置以最大频率20 Hz加载；当试件最大应力在605 MPa及以上时，试验装置以15 Hz加载。

图7 交变荷载波形Fig.7 Alternating load waveform

在疲劳试验中，轴向力控制疲劳试验机荷载频率范围为5～300 Hz，加载频率高时试件在交变荷载作用下会产生较大的热量，从而影响试件的疲劳强度[8]。因此，本次试验中，15～20 Hz的试验加载频率对试验结果的影响较小。

根据文献[11]，低应力水平时试件可能在200万次循环荷载下并未发生疲劳断裂破坏，如果疲劳循环次数达到200万次仍然没有破坏，认为试件满足疲劳性能要求，试件的疲劳极限次数可保守认定为200万次。钢材的疲劳强度是指在规定应力幅内，经受一定次数(200万次)[10- 11]循环荷载后发生疲劳破坏的最大应力值。本次试验通过调整应力水平，最终逐渐逼近疲劳强度。

(3)应力水平

应力水平S在疲劳试验中通常由最大应力和最小应力来表示，由于疲劳试件承受着变化的交变荷载，其所受的最大应力和最小应力体现了试件受力的总体情况。本次试验的应力水平由最大应力决定，设置按照以下几个原则确定：①最大应力取大于0.7倍的试件屈服强度，即0.7fy。②试件应力水平在最大应力与最小应力之间应至少有5个分段区间，区间的间隔随着应力的减小而增大，这主要是由于S-N曲线的形状为幂函数形式曲线，在应力水平比较低时，循环次数的变化比较小。

根据以上原则，笔者制定了如下9个应力水平：400、410、445、480、520、560(0.7fy)、605、650、700 MPa。

1.2.3 试验顺序以及个数选择

本次试验按第1.2.2节确定的9种不同的应力水平开展，每种应力水平的试件数量由以下方法决定：

(1)每种应力水平下准备至少4个试件；

(2)每种应力水平下以3个试件为一组进行试验。当3个试件在200万次往复荷载之内都发生疲劳断裂破坏时，如果3个试件的往复循环次数均在三者平均往复循环次数的±15%以内，则认为该组试验结果离散性较小，在可接受范围之内。如果存在个别试件的往复循环次数在三者平均往复循环次数的±15%以外，则认为该组试验结果的离散性较大，为减小试验结果的离散性，确定更加准确的S-N曲线，开展第4个试件的疲劳试验；

(3)当第1个试件的往复循环次数达到200万次时还未破坏，结束实验，进行第2个试件的疲劳试验。如果得到同样结果时，将该应力水平循环疲劳次数记录为200万次，结束试验；

(4)试验过程中应力水平为445 MPa的试件组试验结果的离散性比较大，各个试件之间的结果偏差最大。因此，为提高精度并准确捕捉疲劳强度值，在该应力水平下进行了6个试件的疲劳试验。

2 试验结果及分析

2.1 试验结果

本次试验中每个试件的试验条件、破坏时的往复循环次数以及最终的破坏形式见表2。以试件破坏时往复循环次数N为横坐标，应力水平S为纵坐标，得到本次试验的往复循环次数和应力水平的散点图及S-N曲线，如图8所示。

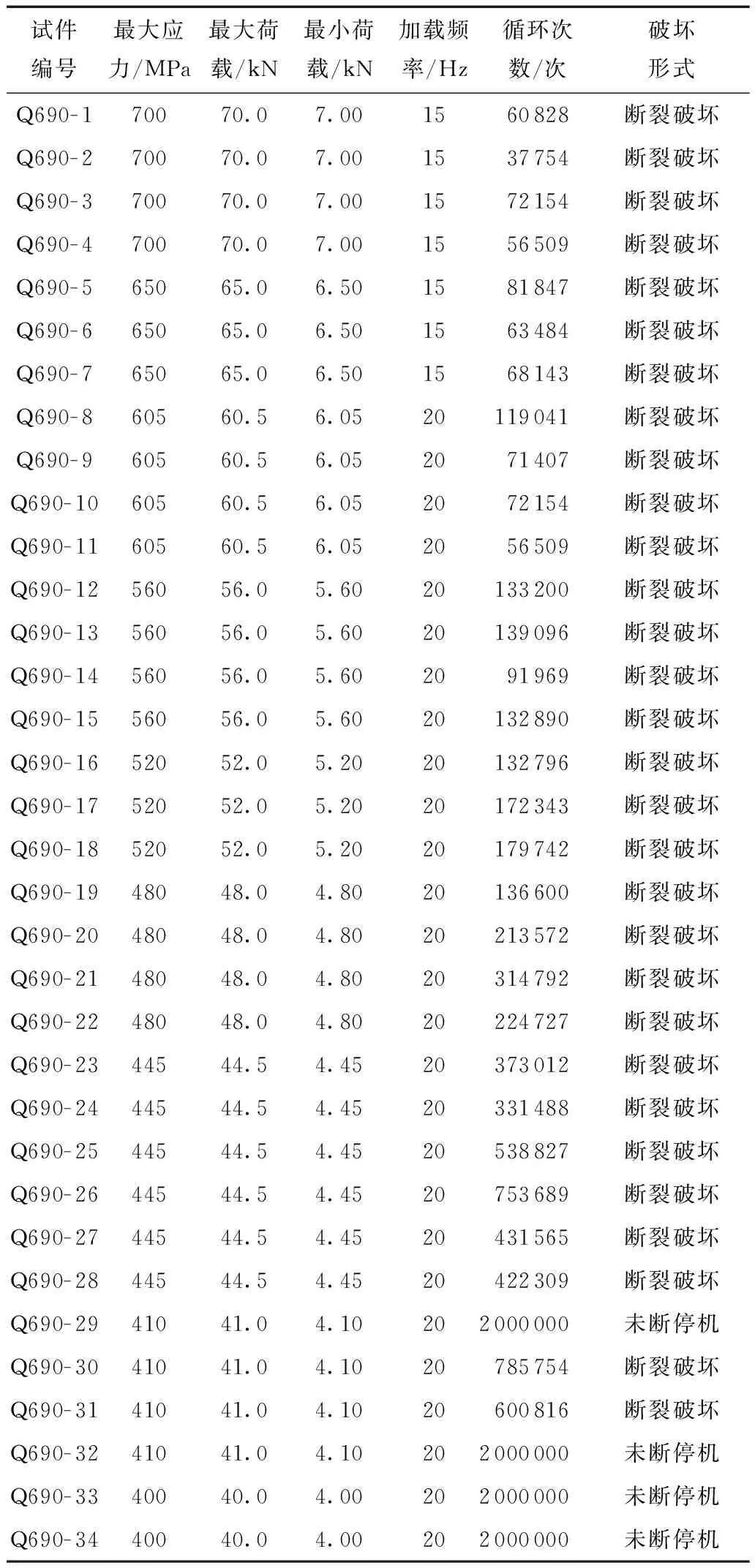
表2 Q690D钢材疲劳试验结果Table 2 Fatigue test results of Q690D steel

图8 Q690D疲劳试验结果散点图及S-N曲线

2.2 断口宏观和微观分析

本次试验的试件断面如图9所示。从试件的断面可以看出，在本次疲劳试验中，所有试件的断面均呈现为两个区域，一个是疲劳纹源及扩展区，一个是瞬时断裂区，应力水平越高，最终瞬时断裂区的区域面积越大。从断口特征来看，疲劳纹源及扩展区比较光滑，瞬时断裂区比较凹凸不平。通过扫描电镜照片可知，本次试验所使用的试件没有杂质，最初的疲劳裂缝在试件表面的初始缺陷处产生，然后以扇形的方式向四周扩展。瞬时断裂区能够观察到一些韧窝，但是疲劳纹源及扩展区未见有韧窝。另外，同样参数下试件高周疲劳寿命的确存在差异较大的情况。对于轧制钢来说，其冶炼、轧制与加工过程中不可避免地会存在非金属杂质、微小孔洞等初始缺陷，而初始缺陷会造成钢材疲劳裂纹的萌生，由于其具有很强的随机性和不确定性，导致了高周疲劳试验结果的离散性。

图9 疲劳试验试件断面以及扫描电镜图

2.3 S-N曲线

疲劳强度是材料在经过多次往复荷载循环后不发生疲劳断裂的指标。材料疲劳强度一般是以S-N曲线来描述。目前国内最常见的是以幂函数的关系式来表达S和N之间的关系，其形式为

(2)

其中，Smax为截面最大应力，N为往复循环次数，参数m、C一般与材料本身的性质、试件的形式、加载应力比和加载方式有关[16]。对等式两边取对数运算，得到

(3)

根据上述的试验结果，采用最小二乘法，得到了Q690D钢的S-N曲线表达式：

lgSmax=-0.149 41lgN+3.512 6

(4)

为了保证拟合公式的精度，对试验结果进行相关系数r的计算，计算公式如下：

(5)

r越接近1，表示lgSmax和lgC两者的线性相关性更强；一般认为相关系数在0.8以上的回归公式才能够达到精度要求，应用于工程实际。本研究中，使用式(5)计算出的相关系数为0.928，即本研究中的S-N曲线表达式和试验实测值之间能够较好地吻合。试验得到的标准差为0.031，当取95%保证率时，式(3)作如下变换：

(6)

式中，σ为对数样本标准差。

经同等变换得到Q690D钢的疲劳试验曲线公式和95%保证率曲线公式如下：

Smax=3 255.367N-0.149 41

(7)

Smax=2 897.781N-0.149 41

(8)

3 Q690D钢材疲劳特性的评价与比较

3.1 与现行规范的对比

为了对Q690D钢材的疲劳性能进行客观的评价，将试验结果与规范给出的计算公式进行比较，根据美国钢结构规范ANSI/AISC 360- 10[17]的疲劳性能计算公式:

(9)

式中：FSR为设计应力范围;Cf为材料的相关参数;FTH为极限疲劳应力范围;根据规范取Cf=250×108，FTH=165 MPa。其中：

FSR=Smax-Smin

(10)

对式(9)进行等价变换得

Smax=22 207.402N-0.333

(11)

此外，根据欧洲钢结构规范BS EN 1993- 1- 9[18]，对于等幅法向应力，当N≤5×106时其疲劳强度计算公式为

(12)

式中，Δσ为应力范围，下标Y表示在Y次循环下的状态，下标C表示在N=2×106时的状态，k为疲劳强度曲线斜率，ΔσC为NC=2×106次循环时的疲劳强度基准值。根据规范要求板材的ΔσC取160 MPa，对式(12)进行等价变换得

Smax=22 398.597N-1/3

(13)

做出与规范对比的S-N曲线，如图10所示。可以看出在相同应力水平下，Q690D钢材的疲劳特性要远远高于规范公式计算的结果，说明规范规定的疲劳性能S-N曲线计算公式对高强钢来说较为保守。

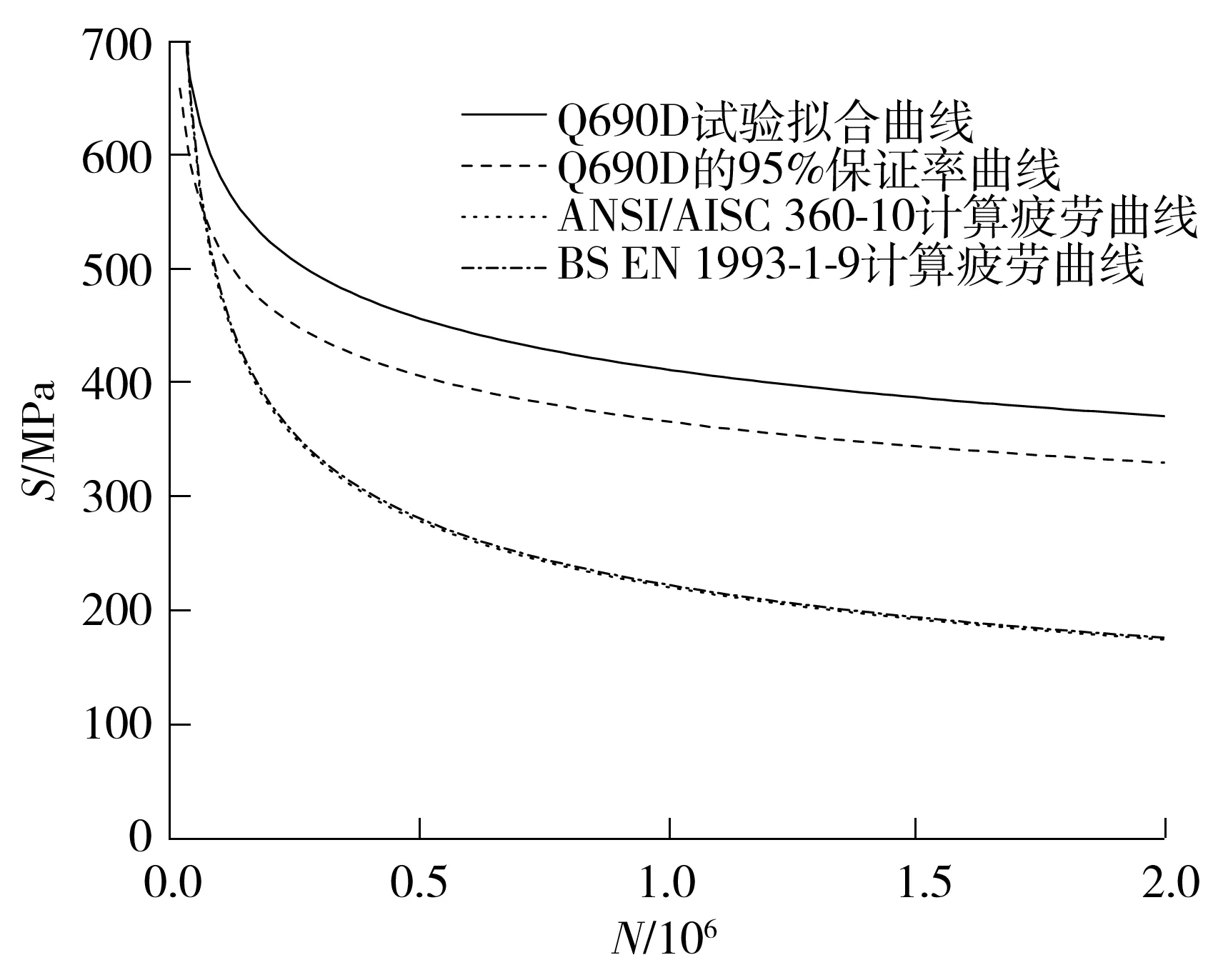
图10 本试验和规范得到的Q690D钢材S-N曲线对比

3.2 与其他强度等级的钢材进行对比

为了更好地比较不同强度等级钢材的疲劳性能，将本研究中的Q690D高强度钢材试验结果与其他文献[8- 12]中已有强度等级钢材的疲劳曲线进行比较。与本次试验相同，将其他钢材试验的原始数据以最小二乘法线性拟合出应力水平和疲劳寿命的对数线性关系式，并等价变换为常用的幂函数形式，求出的各类钢材的S-N曲线列于表3和图11。表4示出了本研究中讨论的不同强度等级钢材疲劳试验的试验条件。

表3 各种强度等级钢材的试验S-N曲线方程

图11 各种钢材的试验S-N曲线Fig.11 Tested S-N curves of various steels

表4 各种强度等级钢材疲劳试验的试验条件

从本研究中的Q690D钢材和以往文献中其他强度等级钢材的S-N曲线比较得到：

(1)从整体上来看，钢材本身材料强度等级越高，S-N曲线就越位于上方。也就是说，疲劳强度与材料的强度等级有关。而钢材的性能又与板件厚度有关，例如Q390GJD采用的板件厚度过大，达到35 mm，对于轧制钢其屈服强度及抗疲劳强度有所下降，曲线与Q345疲劳曲线相近。随着钢板厚度的增加，初始缺陷也随之增加，钢材的疲劳性能因而降低。

(2)对于钢材的疲劳强度，材料强度等级越高，钢材疲劳强度越大。而对于Q420B和Q420C两组数据，试验所得的数据量较少，使得拟合得出的疲劳曲线在200万次处的疲劳强度反而低于强度等级更低的钢材。这说明对于钢材疲劳性能的判定需要较多的数据量支持。

(3)对于同一强度等级的钢材，如Q420B和Q420C两种钢材，材料的疲劳强度和材料本身的钢材质量有关，Q420C对钢材的冲击韧性要求比Q420B要高，钢材质量更好，其疲劳曲线也在Q420B上方。

(4)对于同一种钢材，如Q460，第1组试验数据的离散性较大，拟合出的疲劳试验曲线偏平，疲劳曲线中出现低于强度等级更低的钢材情况，而另一组数据拟合的疲劳曲线符合上述规律(1)。这说明钢材的疲劳试验的离散性不能忽略，同一种类的钢材会因为不同批次的钢材质量不同而出现不同的结果。

4 结论

本研究进行了高强度钢材Q690D的高周疲劳实验，拟合出Q690D钢材的S-N疲劳曲线。此外，通过和规范以及其他强度等级钢材试验得到的S-N疲劳曲线进行比较，综合评价了Q690D钢材的疲劳特性，得出以下结论：

(1)本次高周疲劳试验确定了Q690D高强度钢材的S-N疲劳曲线，计算所得的相关系数为0.928，试验结果离散性较低，能较为精确地评价Q690D高强钢的疲劳特性。

(2)试验所得的疲劳曲线与美国和欧洲钢结构规范的计算结果相比，Q690D的疲劳特性远远高于美国钢结构规范(ANSI/AISC 360- 10)和欧洲钢结构规范(BS EN 1993- 1- 9)的计算结果，按上述规范计算高强钢的疲劳强度有较大的安全储备。

(3)将试验所得的疲劳曲线与其他强度等级的钢材进行对比，可以看出：钢材的疲劳取决于本身的屈服强度，钢材本身质量对其疲劳特性也有一定的影响。

(4)疲劳特性试验所得的数据离散性较大，要想更为精确地得到某一强度等级钢材的疲劳特性曲线，需要较多的试验数据的支持。